蓝桥杯 题库 简单 每日十题 day11

01 质数
质数
题目描述
给定一个正整数N,请你输出N以内(不包含N)的质数以及质数的个数。
输入描述
输入一行,包含一个正整数N。1≤N≤10^3
输出描述
共两行。
第1行包含若干个素数,每两个素数之间用一个空格隔开,素数从小到大输出。
第2行包含一个整数,表示N以内质数的个数。
输入输出样例
示例
输入
10
输出
2 3 5 7
4
#include <iostream>
#include<math.h>
using namespace std;
bool isprime(int n){if(n==2) return true;else{for(int i=2;i<=sqrt(n);i++){if(n%i==0) return false;}}return true;
}
int main(){int x,cnt=0; cin>>x;for(int i=2;i<x;i++){if(isprime(i)){cout<<i<<" ";cnt++;}}
cout<<"\n"<<cnt;
return 0;
}
02 字符统计
字符统计
问题描述
给定一个只包含大写字母的字符出S,请你输出其中出现次数最多的字符。
如果有多个字母均出现了最多次,按字母表顺序依次输出所有这些字母。
输入格式
一个只包含大写字母的字等串S.
输出格式
若干个大写字母,代表答案。
样例输入
BABBACAC
样例输出
AB
#include<iostream>
using namespace std;
int main(){string s;getline(cin,s);int b[10000]={0};for(int i=0;i<s.length();i++){b[s[i]]++;}int max=0;for(int i='A';i<='z';i++){if(b[i]>max){max=b[i];}}for(int i='A';i<='z';i++){if(b[i]==max){cout<<char(i);}}return 0;}
03 大乘积
问题描述
小蓝有30个数,分别为:99,22,51,63,72,61,20,88,40,21,63,30,
11, 18, 99, 12, 93, 16, 7, 53, 64, 9, 28, 84, 34, 96, 52, 82, 51, 77 。
小蓝可以在这些数中取出两个序号不同的数,共有30×29/2=435种取法。
请问这435种取法中,有多少种取法取出的两个数的乘积大于等于2022。
答案提交
这是一道结果填空的题,你只需要算出结果后提交即可。本题的结果为
一个整数,在提交答案时只填写这个整数,填写多余的内容将无法得分。
#include <stdio.h>
#include <stdlib.h>
int main(int argc, char *argv[])
{int i,k,sum=0;int a[30]={99,22,51,63,72, 61, 20, 88, 40, 21, 63, 30, 11, 18, 99, 12, 93, 16, 7,53, 64, 9, 28, 84, 34, 96, 52, 82, 51, 77};
for(i=0;i<30;i++){for(k=i+1;k<30;k++){if(a[i]*a[k]>=2022){sum++;}}
}
printf("%d",sum);
return 0;
}
04 组合数问题

输入输出样例
示例
输入
1 2
3 3
输出
1
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;const ll MOD = 1E9 +7;ll t, k;
ll n, m, ans, len;
ll a[70], b[70];
ll dp[70][4];ll ans0(ll x, ll y) {
// if (x < 0 || y < 0) return 0;if (x <= y) return (x % MOD + 2) * (x % MOD + 1) / 2 % MOD;x %= MOD, y %= MOD;return ((y + 2) * (y + 1) / 2 % MOD + (x - y) * (y + 1) % MOD) % MOD;
}ll ans1(ll x, ll y) {
// if (x < 0 || y < 0) return 0;return min(x, y) + 1;
}ll ans2(ll x, ll y) {
// if (x < 0 || y < 0) return 0;return max(x - y + 1, 0LL);
}int main() {cin >> t >> k;while (t--) {cin >> n >> m;if (m > n) m = n;ans = ans0(n, m);memset(b, 0, sizeof b);for (len = 0; n; len++, n /= k) a[len] = n % k;for (int i = 0; m; i++, m /= k) b[i] = m % k;n = len;
// memset(dp, 0, sizeof dp);dp[n][0] = dp[n][1] = dp[n][2] = 0;dp[n][3] = 1;for (int i = n - 1; i >= 0; i--) {dp[i][0] = dp[i + 1][0] * ans0(k - 1, k - 1);dp[i][0] += dp[i + 1][1] * ans0(a[i] - 1, k - 1) + dp[i + 1][2] * ans0(k - 1,b[i] - 1);dp[i][0] += dp[i + 1][3] * ans0(a[i] - 1, b[i] - 1);dp[i][1] = dp[i + 1][1] * ans1(a[i], k - 1) + dp[i + 1][3] * ans1(a[i], b[i] - 1);dp[i][2] = dp[i + 1][2] * ans2(k - 1, b[i]) + dp[i + 1][3] * ans2(a[i] - 1, b[i]);dp[i][3] = ((a[i] >= b[i]) && dp[i + 1][3]);dp[i][0] %= MOD; dp[i][1] %= MOD;dp[i][2] %= MOD; dp[i][3] %= MOD;}ans -= (dp[0][0] + dp[0][1] + dp[0][2] + dp[0][3]) % MOD;ans = (ans % MOD + MOD) % MOD; cout << ans << endl;}return 0;
}
05 糖果

输入输出样例
示例
输入
1 2
3 3
输出
1
#include<iostream>
using namespace std;
int dp[(1<<20)+1];//dp数组
int n,m,k,a[101];
//状态压缩动态规划(简称状压dp)是另一类非常典型的动态规划,通常使用在NP问题的小规模求解中,虽然是指数级别的复杂度
//该算法主要以二进制的方式 思维
//入门:https://www.cnblogs.com/ibilllee/p/7651971.html https://zhuanlan.zhihu.com/p/131585177
int main()
{fill(dp,dp+(1<<20)+1,0xffff);//初始化 dp数组 cin >> n >> m >> k;//输入 int c[m];//占位数组 有则是1 无为0 fill(c,c+m,0);//用来鉴定是否能全尝到 bool NUL=false;//用来鉴定是否能全尝到 for(int i=1;i<=n;++i)//有n包 {int x=0,y;for(int j=1;j<=k;++j)//每包中的 类型 {//比如有5类糖果即5位 二进制0表示没有 1表示有 如果某一组是有 1(1<<1-1=00001) 3(1<<3-1=00100) 4(1<<4-1=01000) 糖果//然后这一组进行 ‘|’ 或运算 然后就可以表示这一组就是 01101 然后这个数字十进制13就可以表示这个 这一包的种类cin >> y; y--;//上面有过程 解释 x|=(1<<y);//或运算是在(十进制也是在二进制中)二进制中 0|1=1 0|0=0 1|1=1 1<<v相当于乘v个2 //根据二进制可以知道有几种糖果c[y]++; //先检验糖果是否全 只和鉴定是否能全得到有关 }a[i]=x;//将每一包所有的种类给它 }for(int i=0;i<m;i++)//用来鉴定是否能全尝到 if(!c[i])NUL=true;//用来鉴定是否能全尝到 if(NUL)cout <<"-1";//糖果种类不全打印-1 else{dp[0]=0;//初始化 当然下面这个肯定从这里开始的 for(int i=1;i<=n;i++){// (1<<m)-1 - > length(1<<n-1) = n = n个(1) - > (1<<m)-1的意义 for(int j=(1<<m)-1;j>=0;--j)//dp[j|a[i]]=min(dp[j|a[i]],dp[j]+1);//从第一包开始 /** 解释:: dp[j|a[i]] 表示在所有糖果类中的 j|a[i] 类中的 最优解① 当j=0 时 j|a[i]=a[i] dp[a[i]]=1;② 当j=a[i1] 时 dp[[j|a[i2]] 就是 a[i1]与a[i2] 并集的 最优解③ 进一步向上迭代 直至完全 ④ 当计算出j|a[i]=(1)n 时(进制全为一 ) 即包含所有种类 这个就是最终解 */ }cout << dp[(1<<m)-1];//打印最终解 } return 0;
}
06 外卖店优先级

输出描述
输出一个整数代表答案。
输入输出样例
示例
输入
2 6 6
11
5 2
3 1
6 2
2 1
6 2
输出
1
样例解释:
6时刻时,1号店优先级降到3,被移除出优先缓存;2号店优先级升到6,加入优先缓存。所以是有1家店(2号)在优先缓存中。
#include <iostream>
#include <bits/stdc++.h>
using namespace std;
int main()
{int num,m,t;cin>>num>>m>>t;pair<int,int> ti[m];//订单列表int p[num]={0};//存优先级int flag[num]={0};//1表示在优先缓存,0表示不在int last[num]={0};//存对应id外卖店的上一次接订单时间int cnt=0;for(int i=0;i<m;i++)cin>>ti[i].first>>ti[i].second;//读取订单列表sort(ti,ti+m);//按时间升序排列订单for(int i=0;i<m;i++)//遍历订单列表{int tt=ti[i].first,id=ti[i].second-1;if(tt!=last[id])//该外卖店在下一个时刻接到了订单p[id]-=tt-last[id]-1;if(p[id]<0)p[id]=0;if(p[id]<=3)flag[id]=0;p[id]+=2;if(p[id]>5)flag[id]=1;last[id]=tt;}for(int i=0;i<num;i++){p[i]-=t-last[i];if(p[i]<=3)flag[i]=0;}int ans=0;for(int i=0;i<num;i++)if(flag[i]==1)ans++;cout<<ans;return 0;
}
07 完全二叉树的权值
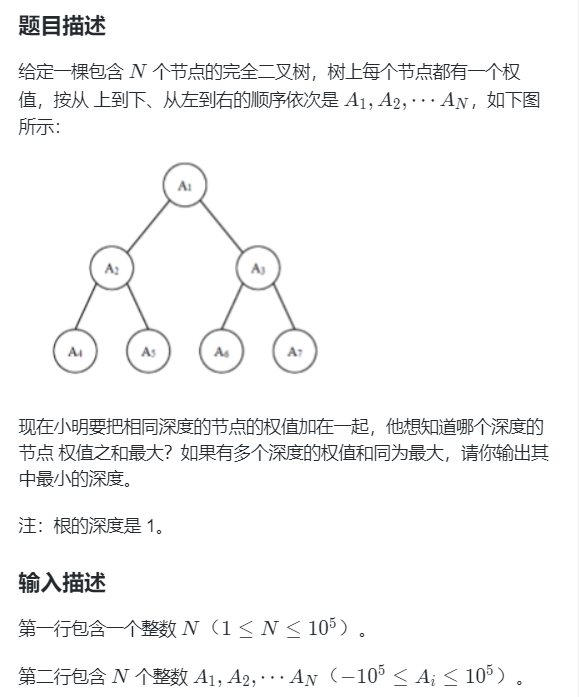
输出描述
输出一个整数代表答案。
输入输出样例
示例
输入
7
1 6 5 4 3 2 1
输出
2
#include<bits/stdc++.h>
using namespace std;
int sum[10008] = {0};
int main()
{int n;int w;int ans;int maxn = 0;cin >> n;for(int i = 1; i <= n; i++){cin >> w;int d = ceil(log(i+1)/log(2));sum[d] += w;}for(int i = 1; i < 10008; i++){if(sum[i] > maxn){maxn = sum[i];ans = i;}}cout << ans;return 0;
}
08 修改数组

输入输出样例
示例
输入
5
2 1 1 3 4
输出
2 1 3 4 5
#include <iostream>
using namespace std;
int main()
{int n;int a[100005]={0}, b[1000005] = { 0 };cin >> n;for (int i = 0; i < n; i++){cin >> a[i];while (b[a[i]] != 0){b[a[i]]++;a[i]+=(b[a[i]]-1);}b[a[i]]++;cout << a[i] << ' ';}return 0;
}
09 小明的背包1

输入输出样例
示例1
输入
5 20
1 6
2 5
3 8
5 15
3 3
输出
37
#include <stdio.h>
#include <stdlib.h>
int val[1001],v[1001],dp[1001][1001]={0};//dp第一个为物品下标,第二个为背包体积,值为价值(确定dp数组以及下标的含义)
int n,V;
int max(int a,int b)
{return a>b?a:b;
}
void backpack()
{for(int i=v[0];i<=V;i++){dp[0][i]=val[0];// 当背包容量大于物品0的容量时,将物品0放入到背包中}for(int i=1;i<=n;i++){for(int j=1;j<=V;j++)//先遍历物品,再遍历体积{if(j<v[i])//当前背包体积小于物品体积dp[i][j]=dp[i-1][j];//不放,价值不变,i-1相当于没放物品i之前的else{dp[i][j]=max(dp[i-1][j],dp[i-1][j-v[i]]+val[i]);//比较放之前和放之后的价值//放之后的价值=放之前的价值+物品i的价值//j-v[i]表示放了物品i,还剩下j-v[i]的容量可以放其他物品//dp[i-1][j-v[i]],表示不放物品i时,背包的容量也减去物品i的容量之后,背包所能放的最大价值}}}
}
int main()
{scanf("%d%d",&n,&V);for(int i=0;i<n;i++)scanf("%d %d",&v[i],&val[i]);backpack();printf("%d",dp[n][V]);return 0;
}
10 求阶乘
问题描述
满足N!的末尾恰好有K个0的最小的N是多少?
如果这样的N不存在输出-1。
输入格式
一个整数K。
输出格式
一个整数代表答案。
样例输入
2
样例输出
10

#include <stdio.h>
#include <stdlib.h>
#include <math.h>
//末尾有几个0取决于从1到N的因子中2和5的组合个数
//因为5的倍数个数比2少,所以只要计算5的倍数个数
//满足5^p<=N的个数,复杂度为O(logN),又因为N越大,末尾的0越多,所以可以用二分找到答案
//此函数用于计算因子5的个数
long long int js( long long int a )
{long long int ans = 0;while ( a > 0 ){ans += a / 5; //因为遇见 5^2要加两个0 5^3要加三个零 以此类推a/=5;}return ans;
}
int main(int argc, char *argv[])
{long long int k;scanf("%lld",&k);long long int l = 1, r = pow(2,63)-1;//pow(2,63)-1表示N的最大值//从1到N的阶乘中5的倍数个数计算出来,再用与k比较的二分法查找出最小的N!while(l<r){long long int mid = l + ( r - l ) / 2;if ( js(mid) < k ) l = mid + 1;else r = mid;}long long int ans = js(l);if ( ans == k ) printf("%lld",l);//如果找到打印,否则打印-1;else printf("%d",-1);// 请在此输入您的代码return 0;
}
相关文章:

蓝桥杯 题库 简单 每日十题 day11
01 质数 质数 题目描述 给定一个正整数N,请你输出N以内(不包含N)的质数以及质数的个数。 输入描述 输入一行,包含一个正整数N。1≤N≤10^3 输出描述 共两行。 第1行包含若干个素数,每两个素数之间用一个空格隔开&…...
dart flutter json 转 model 常用库对比 json_serializable json_model JsonToDart
1.对比 我是一个初学者,一直跟着教材用原生的json,最近发现实在太麻烦了.所以搜索了一下,发现真的有很多现成的解决方案. 网页 https://app.quicktype.io/?ldart 这个是测试下来最好用的 有很多选项,可以使用 json_serializable 也可以不使用 json_serializable 这是推荐最…...

nginx启用了自动目录列表功能的安全漏洞修复方法
一、前言 最近被扫描到安全漏洞,说是nginx启用了自动目录列表功能,现象就是访问http://localhost/file就能看到服务器上的目录 二、修复方法 1.把nginx.conf中的autoindex on改为autoindex off location /file {alias /myuser/userfile/file;autoi…...

vector向量类使用
向量是最简单的 STL 容器,其数据结构与数组相似,占据着一个连续的内存块。 由于内存位置是连续的,所以向量中的元素可以随机访问,访问向量中任何一个元素的时间也是固定的。存储空间的管理是自动的,当要将一个元素插入…...

【Java 进阶篇】MySQL多表查询:内连接详解
MySQL是一种强大的关系型数据库管理系统,允许您在多个表之间执行复杂的查询操作。本文将重点介绍MySQL中的多表查询中的一种重要类型:内连接(INNER JOIN)。内连接用于检索满足两个或多个表之间关联条件的行,它能够帮助…...
C理解(四):链表
本文主要探讨单链表与双链表相关知识。 linux内核链表(include/linux/list.h) 内核链表中纯链表封装,纯链表的各种操作函数(节点创建、插入、删除、遍历),纯链表内嵌在驱动结构体中,实现驱动的创建、插入、删除、遍历等 单链表 单链表链表头插…...
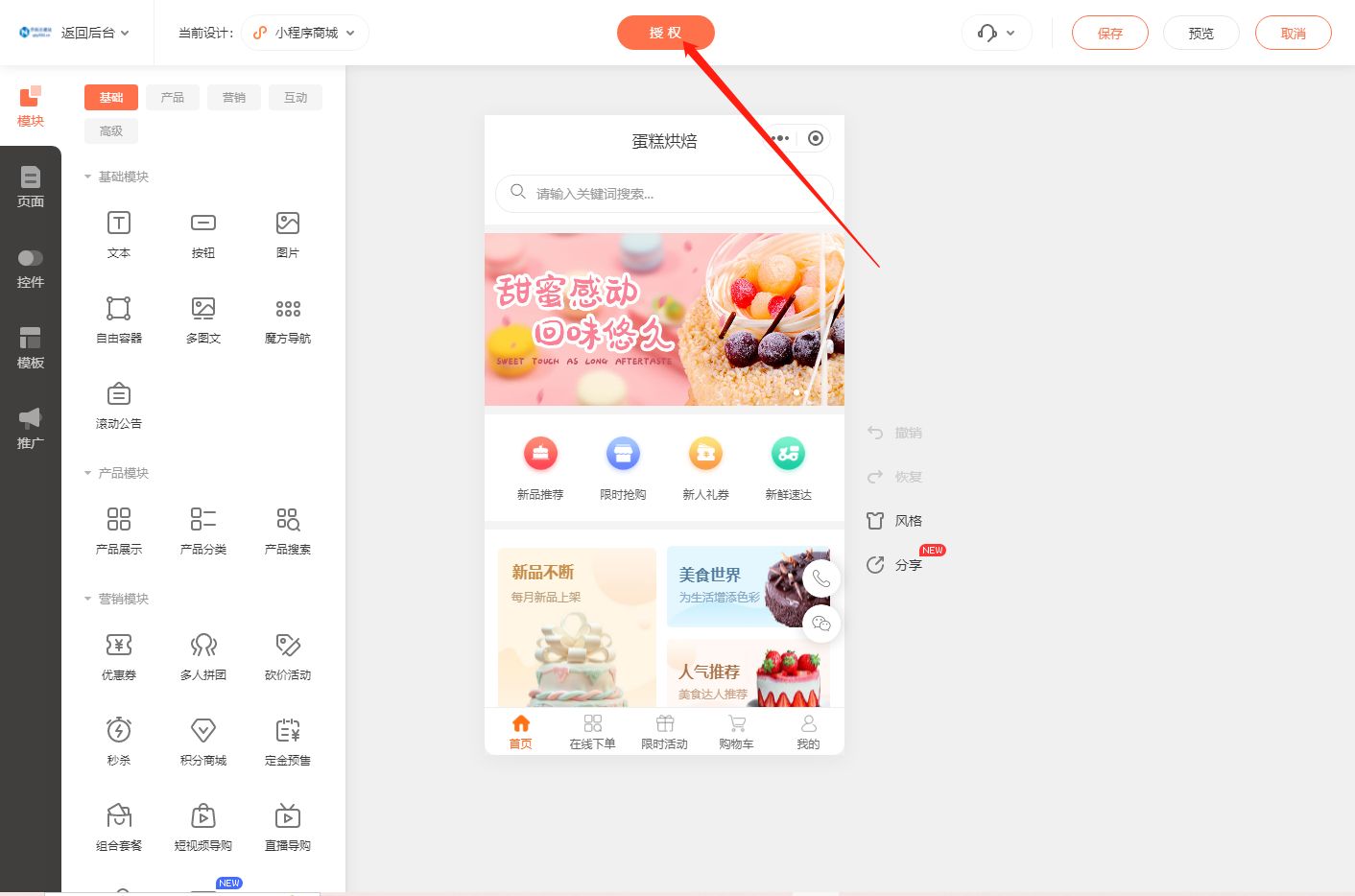
新手教程,蛋糕小程序的搭建流程一网打尽
作为一名新手,想要搭建一个蛋糕小程序可能会觉得有些困惑。但是,不用担心!今天我将为大家详细介绍蛋糕小程序的搭建流程,并带大家一步步完成。 首先,我们需要登录乔拓云网的后台。在登录成功后,点击进入商城…...

springcloud之自我介绍
写在前面 在这篇文章 中我们分析了单体应用的问题,以及用来解决这些问题的解决的方案微服务,并接着看了微服务需要考虑的各种,如服务调用,负载均衡,服务治理,链路追踪,分布式事务,等…...
机器学习之神经网络的层次
文章目录 神经网络组成神经网络根据结构分类神经网络的信号传递 神经网络组成 大脑是一个巨大的神经元网络,所以神经网络是一个节点网络。根据节点的连接方式,可以创建多种神经网络。最常用的神经网络类型之一采用了如图所示的节点分层结构 正方形节点组…...
力扣每日一题(+日常水几道题)
每日一题1333. 餐厅过滤器 - 力扣(LeetCode) 简单的按规则排序,去除几个不满足的条件然后排序返回即可 #include<algorithm> class Solution { public:vector<int> filterRestaurants(vector<vector<int>>& restaurants, …...

百度SEO不稳定的原因及解决方法(百度SEO不稳定因素的5大包括)
百度SEO优化不稳定介绍:蘑菇号-www.mooogu.cn 随着百度SEO算法的不断变化和升级,许多网站的SEO排名经常出现不稳定的情况,这种情况在一定程度上影响了网站的流量和排名,导致网站的质量评分降低。因此,深入分析百度SEO…...
深度学习(1)---卷积神经网络
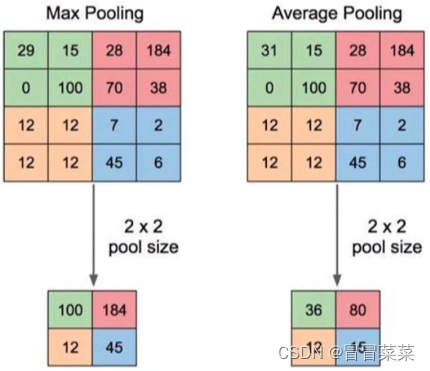
文章目录 一、发展历史1.1 CNN简要说明1.2 猫的视觉实验1.3 新认知机1.4 LeNet-51.5 AlexNet 二、卷积层2.1 图像识别特点2.2 卷积运算2.3 卷积核2.4 填充和步长2.5 卷积计算公式2.6 多通道卷积 三、池化层 一、发展历史 1.1 CNN简要说明 1. 卷积神经网络(Convolut…...

探索社会工程的深度:从定义到高级攻击策略
在广阔的网络安全领域,社会工程作为一种微妙的威胁而出现,它利用人类的漏洞来访问敏感信息或实施欺诈。网络安全背景下的社会工程的定义很明确:它包括使用欺骗手段操纵个人泄露机密或个人信息,然后将这些信息用于欺诈目的。 此类…...

CTF 入门指南:从零开始学习网络安全竞赛
文章目录 写在前面CTF 简介和背景CTF 赛题类型介绍CTF 技能和工具准备好书推荐 写作末尾 写在前面 CTF比赛是快速提升网络安全实战技能的重要途径,已成为各个行业选拔网络安全人才的通用方法。但是,本书作者在从事CTF培训的过程中,发现存在几…...

Spring整合第三方框架
目录 Spring整合第三方框架 加载外部properties文件 自定义命名空间解析原理 自定义命名空间总结和案例需求 总结 案例 Spring整合第三方框架 加载外部properties文件 Spring整合第三方框架不像MyBatis那么简单了,例如Dubbo框架在与Spring框架整合时…...

Linux Shell 无vi获取文件某行指定内容和修改某行指定内容
注意:操作之前一定要先备份!!!一定要先备份!!!一定要先备份!!! 1. 获取某配置文件中某一行某项的值 cat /sshd_config |grep "PermitRootLogin" …...

在EXCEL中构建加载项之创建加载项的目的及规范要求
【分享成果,随喜正能量】一句南无阿弥陀佛,本是释迦牟尼佛所证的无上正等正觉法,洒在娑婆世界的众生海中,只为末世众生能够以信愿之心抓住此救命稻草,要知道今世人此生的处境,可能只剩这道要么极乐要么三涂…...
Hive【Hive(三)查询语句】
前言 今天是中秋节,早上七点就醒了,干啥呢,大一开学后空教室紧缺,还不趁着假期来学校等啥呢。顺便偷偷许个愿吧,希望在明年的这个时候,秋招不知道赶不赶得上,我希望拿几个国奖,蓝桥杯…...
商场做小程序商城的作用是什么?
商场是众多商家聚集在一起的购物公共场所,大商场也往往入驻着众多行业商家,是每个城市重要的组成部分。 随着互联网电商深入及客户消费行为改变,不少商场如今的客流量非常有限,甚至可以说是员工比客人多,这就导致撤店…...
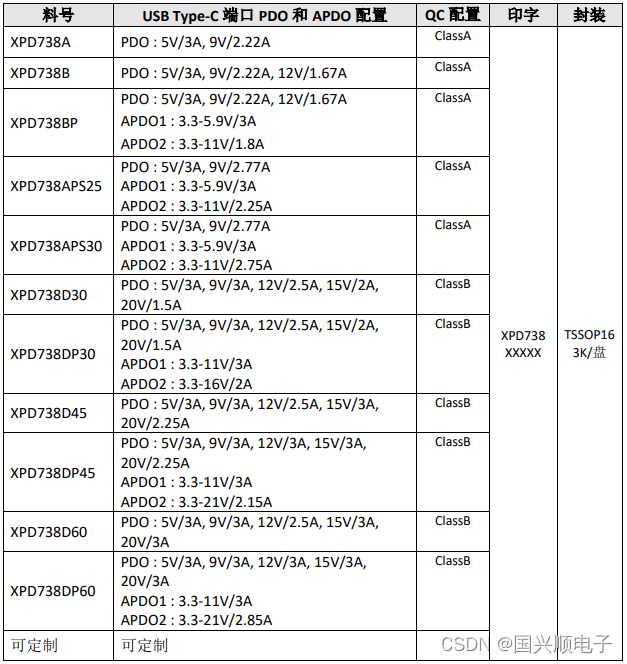
XPD738协议系列-USB Type-C PD 和 Type-A 双口控制器
产品描述: XPD738 是一款集成 USB Type-C、USB Power Delivery(PD)2.0/3.0 以及 PPS、QC3.0/QC3.0/QC2.0 快充协议、华为 FCP/SCP/HVSCP 快充协议、三星 AFC 快充协议、BC1.2 DCP 以及苹果设备 2.4A 充电规范的多功能 USB Type-C 和 Type-A …...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

SciencePlots——绘制论文中的图片
文章目录 安装一、风格二、1 资源 安装 # 安装最新版 pip install githttps://github.com/garrettj403/SciencePlots.git# 安装稳定版 pip install SciencePlots一、风格 简单好用的深度学习论文绘图专用工具包–Science Plot 二、 1 资源 论文绘图神器来了:一行…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

基于TurtleBot3在Gazebo地图实现机器人远程控制
1. TurtleBot3环境配置 # 下载TurtleBot3核心包 mkdir -p ~/catkin_ws/src cd ~/catkin_ws/src git clone -b noetic-devel https://github.com/ROBOTIS-GIT/turtlebot3.git git clone -b noetic https://github.com/ROBOTIS-GIT/turtlebot3_msgs.git git clone -b noetic-dev…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

day36-多路IO复用
一、基本概念 (服务器多客户端模型) 定义:单线程或单进程同时监测若干个文件描述符是否可以执行IO操作的能力 作用:应用程序通常需要处理来自多条事件流中的事件,比如我现在用的电脑,需要同时处理键盘鼠标…...
