机器学习——一元线性回归构造直线,并给出损失函数
目 录
Question
问题分析
1.概念补充
2.流程分析
3.注意
具体实现
最终成果
代码
思考:
Question
在二维平面有n个点,如何画一条直线,使得所有点到该直线距离之和最短
如果能找到,请给出其损失函数
问题分析
1.概念补充
关于损失函数:
也即代价函数,是一个量化误差的表达式
参考链接:线性回归与非线性回归:1.0一元线性回归与代价函数(损失函数)_在一元线性回归中,哪个函数不适用于损失函数(-CSDN博客
本文中我们采用`观测值与实际值差的平方`作为损失函数
具体原理参考链接:知乎形象举例——梯度下降算法
下面是MSE函数,但是我这里就没有除以2了,所以偏导应当有一个2倍
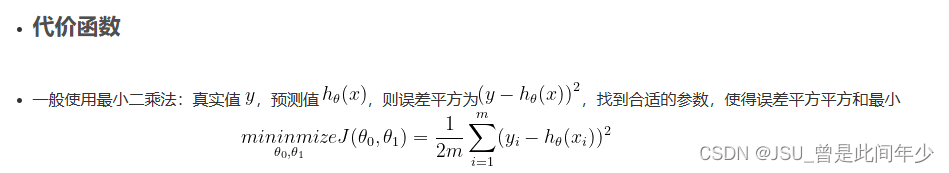
2.流程分析
对于此问题,我们应当按如下步骤进行求解
首先,我们需要对于指定初始的k与b初始化该直线
然后,对学习率(也即步长)和迭代次数进行适当调整
最后,在得到满意的结果后终止调整,整理结果,给出最终参数
3.注意
我们用的并不是直线距离进行损失计算,而是用的△y进行计算,
但是结果并没有影响,因为经过推倒后,距离d与△y成正比
具体实现
本文参考多方资料,使用python代码手写一元线性回归进行求解
计算当前参数下的最小二乘法结果:
def calcLoseFunction(k,b,XData,YData):sum=0for i in range(0,listSize):# 使用偏离值的平方进行累和sum+=(YData[i]-(k*XData[i]+b))**2return sum梯度下降法进行搜索:
#梯度下降法
def calcGradientCorrection(b, k, XData, YData, learningRate, bfsNums):for i in range(0, bfsNums):sumk, sumb = 0, 0for j in range(0, listSize):# 定义预测值Y'normalNum = k * XData[j] + b# 计算逆梯度累和sumk += -(1 / listSize) * (normalNum - YData[j]) * XData[j]sumb += -(1 / listSize) * (normalNum - YData[j])# 在逆梯度的方向上进行下一步搜索k += learningRate * sumkb += learningRate * sumbreturn k, b最终成果
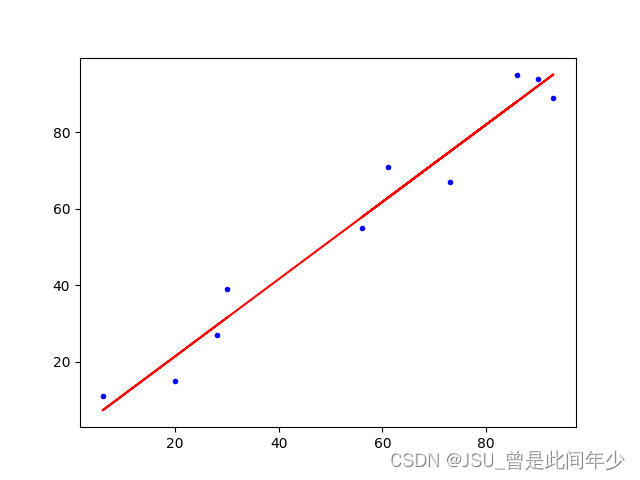
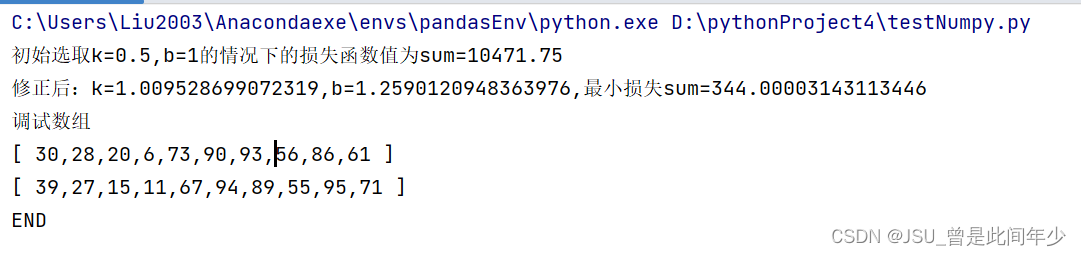
采用随机来对点进行生成,大部分测试较为稳定,模型较为拟合
但是由于X,Y都进行随机生成,按照期望来说,在100*100的矩阵范围内数据呈现均匀分布
于是改造Y数据生成方式为:
YData=[XData[i]+generateRandomInteger(-10,10) for i in range(listSize) ]调整初始斜率k=0.5进行测试,最终结果较为拟合,效果较好
代码
import numpy #发现直接用List就行了
import random
import matplotlib.pyplot as plt
# random.random()
# random.randint(start,stop)
#################全局数据定义区
# 数组大小
listSize=10
# 定义学习率 取尽量小0.001
learningRate=0.0001
#定义初始直线的 斜率k 和 截距b 45° 1单位距离
# 现在设置 k=0.5 检验程序
k,b=0.5,1
#定义迭代次数
bfsNums=9999
#################全局数据定义区END
# 生成随机数
def generateRandomInteger(start, end):# [1-100]return random.randint(start, end)# 打印本次随机生成的X,Y 便于快速粘贴复现
def printXYArray(XData,YData):# 打印Xprint("[", ",".join([str(i) for i in XData]), "]")# 打印Yprint("[", ",".join([str(i) for i in YData]), "]")# 最小二乘法定义损失函数 并计算
#参考链接:https://blog.csdn.net/zy_505775013/article/details/88683460
# 求最小二乘法的最小值 最终结果应当是在learningRate一定情况下 这个最小的sum
def calcLoseFunction(k,b,XData,YData):sum=0for i in range(0,listSize):# 使用偏离值的平方进行累和sum+=(YData[i]-(k*XData[i]+b))**2return sum#梯度下降法
def calcGradientCorrection(b, k, XData, YData, learningRate, bfsNums):for i in range(0, bfsNums):sumk, sumb = 0, 0for j in range(0, listSize):# 定义预测值Y'normalNum = k * XData[j] + b# 计算逆梯度累和 注意这里求偏导应当是两倍 不知道为什么写成1了# 求MSE的偏导sumk += -(2 / listSize) * (normalNum - YData[j]) * XData[j]sumb += -(2 / listSize) * (normalNum - YData[j])# 在逆梯度的方向上进行下一步搜索k += learningRate * sumkb += learningRate * sumbreturn k, b# 随机生成横坐标
XData=[generateRandomInteger(1,100) for i in range(listSize) ]
# 随机生成纵坐标
YData=[XData[i]+generateRandomInteger(-10,10) for i in range(listSize) ]
# 纯随机生成 但是可视化效果不直观
# YData=[generateRandomInteger(1,100) for i in range(listSize) ]
# 死值替换区
# XData=testArrayX
# YData=testArrayYprint("初始选取k={},b={}的情况下的损失函数值为sum={}".format(k,b,calcLoseFunction(k,b,XData,YData)))
# 对k,b进行梯度修正
k,b=calcGradientCorrection(b,k,XData,YData,learningRate,bfsNums)
print("修正后:k={},b={},最小损失sum={}".format(k,b,calcLoseFunction(k,b, XData, YData)))
print("调试数组")
printXYArray(XData,YData)#画图
plt.plot(XData, YData, 'b.')
plt.plot(XData, k*numpy.array(XData)+b, 'r')
plt.show()
print("END")思考:
如果替换在三维空间会怎么样,如何去求?
答:在三维空间内,我们就需要对三个变量(K1,K2,b)进行偏导求解,然后同样在逆梯度方向上搜索求解。注意要替换对应的损失函数,将直线方程进行替换即可!
相关文章:

机器学习——一元线性回归构造直线,并给出损失函数
目 录 Question 问题分析 1.概念补充 2.流程分析 3.注意 具体实现 最终成果 代码 思考: Question 在二维平面有n个点,如何画一条直线,使得所有点到该直线距离之和最短 如果能找到,请给出其损失函数 问题分析 1.概念…...
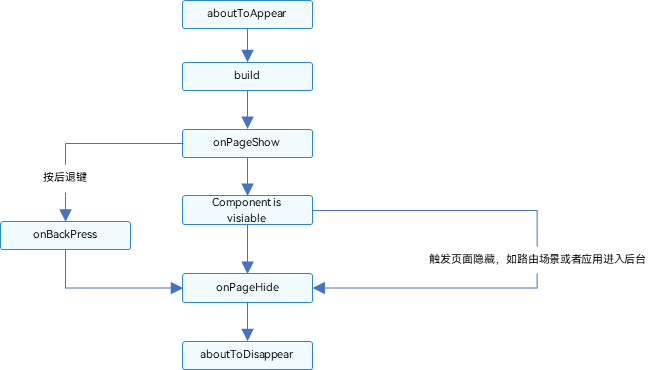
OpenHarmony自定义组件介绍
一、创建自定义组件 在ArkUI中,UI显示的内容均为组件,由框架直接提供的称为系统组件,由开发者定义的称为自定义组件。在进行 UI 界面开发时,通常不是简单的将系统组件进行组合使用,而是需要考虑代码可复用性、业务逻辑…...
云原生之使用Docker部署PDF多功能工具Stirling-PDF
云原生之使用Docker部署PDF多功能工具Stirling-PDF 一、Stirling-PDF介绍1.1 Stirling-PDF简介1.2 Stirling-PDF功能 二、本次实践规划2.1 本地环境规划2.2 本次实践介绍 三、本地环境检查3.1 检查Docker服务状态3.2 检查Docker版本3.3 检查docker compose 版本 四、下载Stirli…...
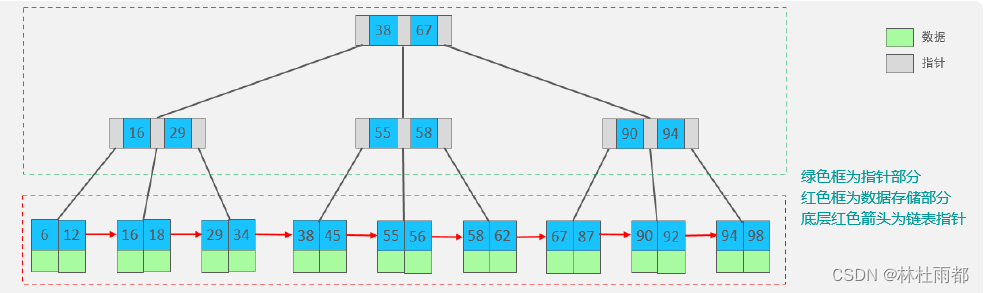
B树和B+树的介绍和对比,以及MySQL为何选择B+树
在计算机科学中,B树和B树是常用的数据结构,用于在大规模数据集上进行高效的插入、删除和查找操作。它们在数据库管理系统、文件系统等许多实际应用中发挥着重要作用。本文将深入介绍B树和B树的结构特点、实际应用方面以及它们的优缺点,并最后…...

MD5 绕过第一式:弱比较绕过
文章目录 参考环境MD5韧性脆弱性md5() 隐式类型转换字符串连接数学运算布尔判断相等运算符 科学计数法科学计数法前缀 0E 与 0e PHP8 与 PHP 其他版本下字符串转化为数值的具体规则PHP8数值字符串优化 其他版本更为详细的讲解 字符串与字符串的弱比较字符串与数值的弱比较0e215…...
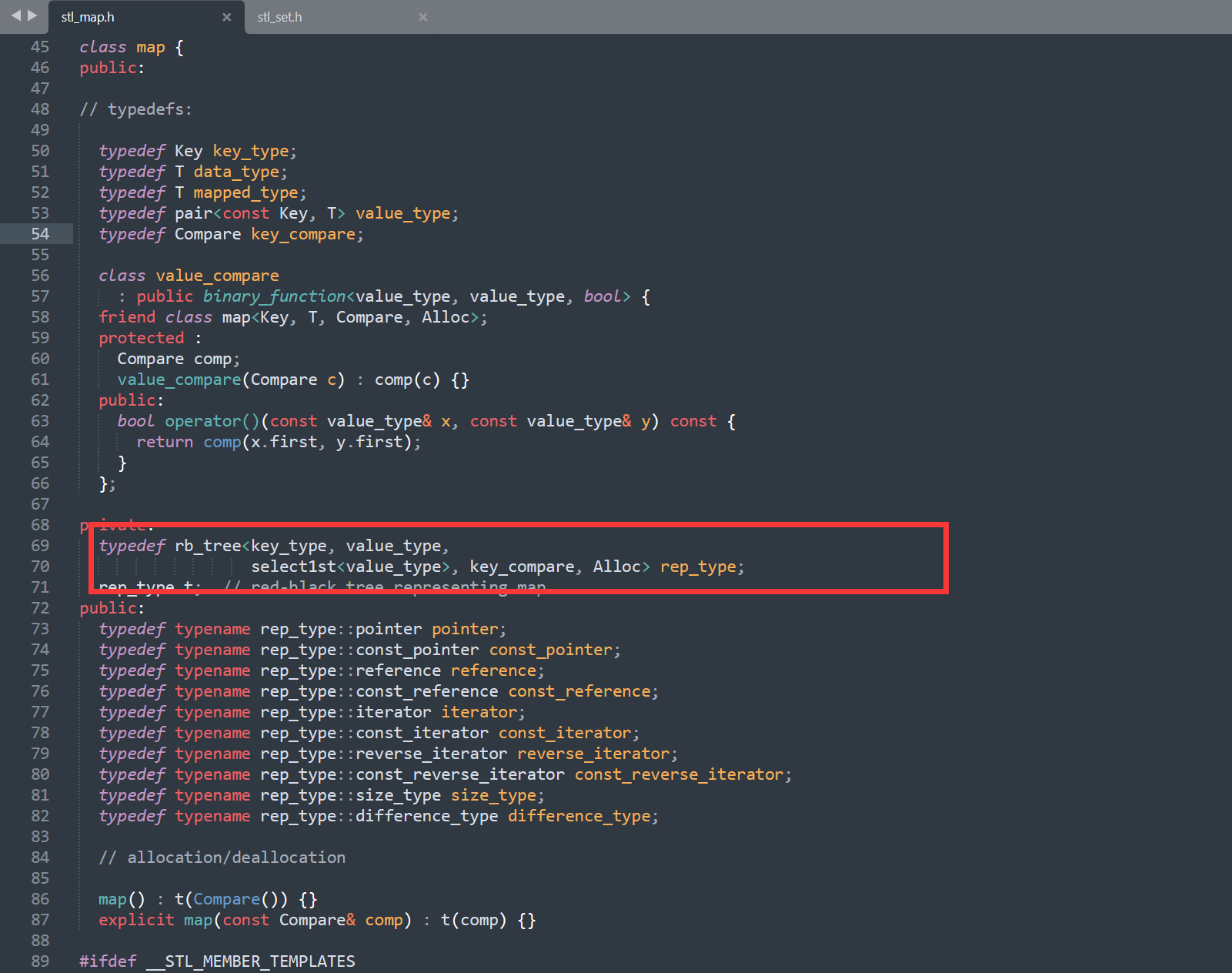
红黑树是如何实现的?
文章目录 一、红黑树的概念二、红黑树的性质三、红黑树和AVL树对比四、红黑树的插入1. 红黑树的结点定义2. 父亲的颜色3. 叔叔的颜色为红色4. 叔叔不存在5. 叔叔存在且为黑6. 插入的抽象图 五、红黑树的验证1. 检查平衡2. 计算高度与旋转次数3. 验证 六、 红黑树与AVL树的比较 …...

实验室没人导该怎么办
实验室没人教该怎么办 Q: 国内top5高校研一,课题开始老板就给了一个大方向,之后怎么做实验都是自己看文献研究的,终于开始动手做实验,才发现别人根本不想管你,宁愿抱着电脑看剧也不想教你,十分焦虑,该怎么办? A: 按照大多数实验室的惯例,老板一定会指派一个小老板…...
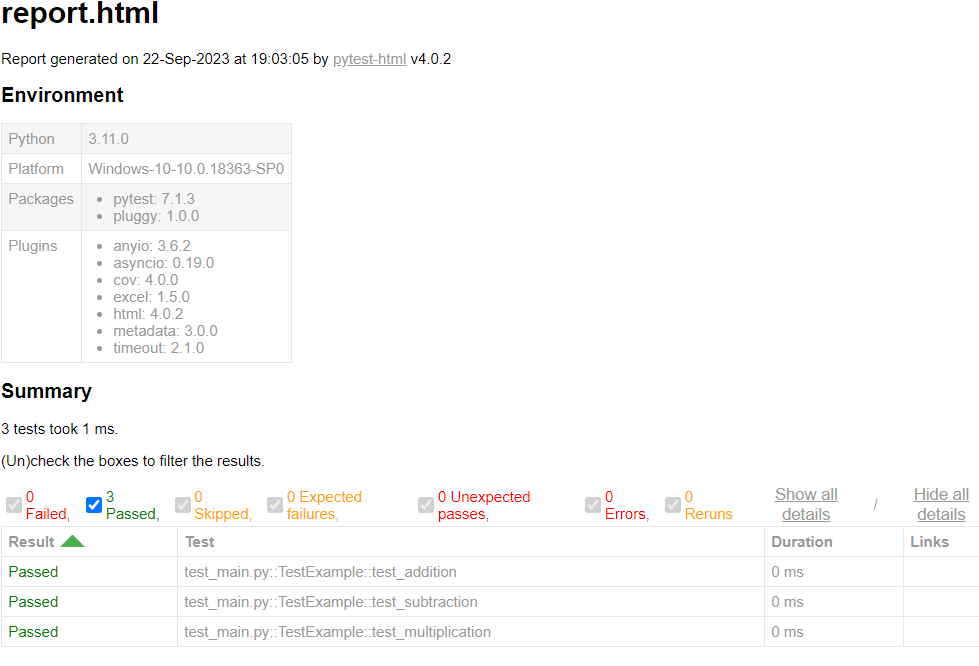
pytest简明教程
1. 简介 pytest是一款基于Python的测试框架。与Python自带的unittest相比,pytes语法更加简洁,断言更加强大,并且在自动测试以及插件生态上比unittest都要更加强大。 1.1. 安装pytest pip install pytest1.2. pytest命名规则 pytest默认会…...

解决方案:解决https页面加载http资源报错
HTTPS页面加载HTTP资源会报错的原因是出于安全性考虑。 HTTPS(HyperText Transfer Protocol Secure)是一种通过使用SSL/TLS加密通信来保护数据传输的协议,它确保了客户端和服务器之间的安全连接。 当HTTPS页面尝试加载非加密的HTTP资源时&a…...
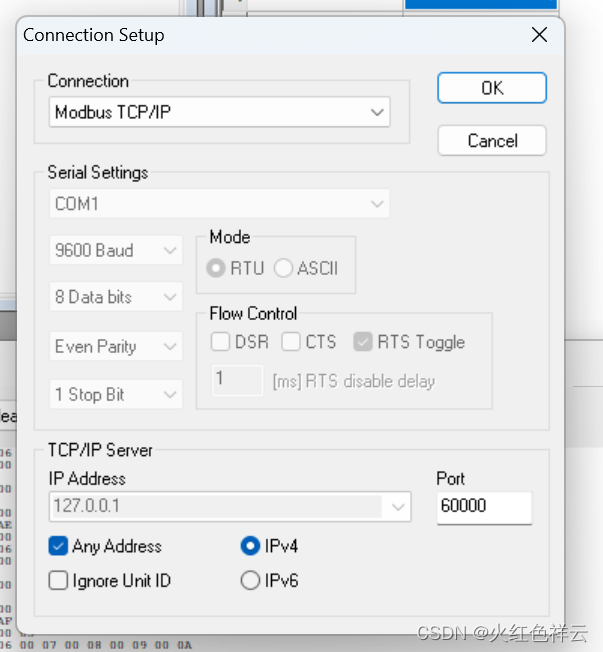
嵌入式开源库之libmodbus学习笔记
socat 安装sudo apt-get install socat创建终端 socat -d -d pty,b115200 pty,b115200查看终端 ls /dev/pts/ minicom 安装 sudo apt-get install minicom链接虚拟终端 sudo minicom -D /dev/pts/3以十六进制显示 minicom -D /dev/pts/1 -H设置波特率 minicom -D /dev/pts/1…...

Spring MVC 中的数据验证技术
一、前言 在Web开发中,数据验证是不可或缺的一部分。Spring MVC 框架提供了强大的数据验证支持,可以帮助我们轻松地对用户提交的数据进行验证。 二、实现 Spring MVC 使用 JSR-303 验证规范(Hibernate Validator 是其参考实现)…...
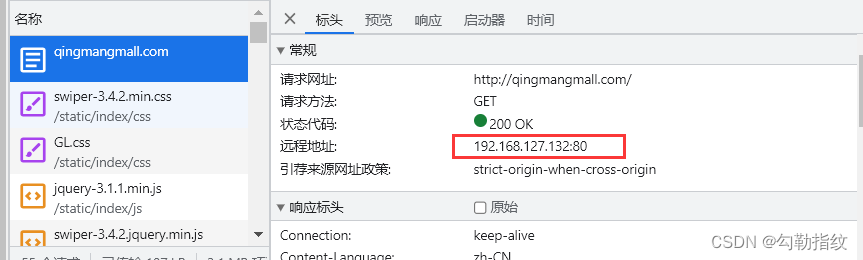
windows 修改hosts映射,可以ping通,但是无法通过http url 路径访问,出现 500 Internal Privoxy Error
问题描述 今天在学习nginx时,想在hosts配置一个nginx的域名映射,但是发现访问nginx服务的ip时可以访问通,在dos命令窗口ping配置的域名映射也可以ping通,但是一旦在浏览器通过http请求访问配置的hosts域名映射时却出现 500 Inter…...

如何将图片转为ico格式
这里主要是记录一个网站,如果你有更好的办法欢迎留言~ ico简介 ICO(Icon)是一种用于表示图标的文件格式,常用于Windows操作系统中。ICO格式的图片通常用于表示应用程序、文件夹、网站等的图标。 ICO文件可以包含多个图标&#x…...

ElasticSearch - 基于 JavaRestClient 操作索引库和文档
目录 一、RestClient操作索引库 1.1、RestClient是什么? 1.2、JavaRestClient 实现创建、删除索引库 1.2.1、前言 1.2.1、初始化 JavaRestClient 1.2.2、创建索引库 1.2.3、判断索引库是否存在 1.2.4、删除索引库 1.3、JavaRestClient 实现文档的 CRUD 1.3…...

【人脸质量评估】MagFace:一个既可以用作人脸识别,又可以用作人脸质量评估的方法
论文题目:《MagFace: A Universal Representation for Face Recognition and Quality Assessment》-CVPR2021 论文地址:https://arxiv.org/abs/2103.06627v4 代码地址:https://github.com/IrvingMeng/MagFace...

FPGA 图像缩放 千兆网 UDP 网络视频传输,基于RTL8211 PHY实现,提供工程和QT上位机源码加技术支持
目录 1、前言版本更新说明免责声明 2、相关方案推荐UDP视频传输--无缩放FPGA图像缩放方案我这里已有的以太网方案 3、设计思路框架视频源选择ADV7611 解码芯片配置及采集动态彩条跨时钟FIFO图像缩放模块详解设计框图代码框图2种插值算法的整合与选择 UDP协议栈UDP视频数据组包U…...
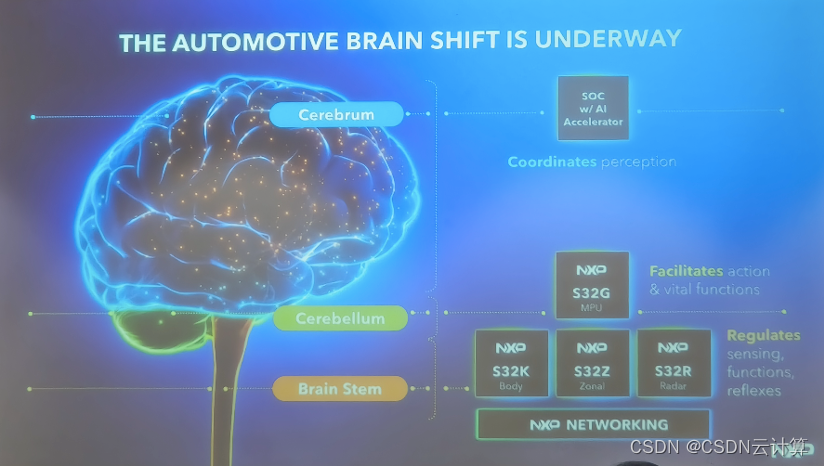
智能驾驶、智能家居、智能工业中的 AI 关键基础设施,半导体厂商恩智浦的角色是什么?
我们来看一条七年前的真实新闻报道,2016 年《福布斯》在报道中提到“2020 年会有 1000 万台的自动驾驶汽车”。然而 2023 年的现在,真正实现 L4 级别自动驾驶的汽车,仍然远远没有达到这个预测的数量。 另一边,数据显示,…...

APScheduler包——python tornado框架中实现定时任务
介绍: APScheduler的全称是Advanced Python Scheduler。它是一个轻量级的 Python 定时任务调度框架。APScheduler 支持三种调度任务:固定时间间隔,固定时间点(日期),Linux 下的 Crontab 命令。同时…...

BASH shell脚本篇3——字符串处理
这篇文章介绍下BASH shell中的字符串处理的相关命令。之前有介绍过shell的其它命令,请参考: BASH shell脚本篇1——基本命令 BASH shell脚本篇2——条件命令 Bash字符串也是一种数据类型,它用于表示文本而不是数字,它是一组可能…...

【SSL】用Certbot生成免费HTTPS证书
1. 实验背景 服务器:CentOS7.x 示例域名: www.example.com 域名对应的web站点目录: /usr/local/openresty/nginx/html 2. 安装docker # yum -y install yum-utils# yum-config-manager --add-repo https://download.docker.com/linux/ce…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

Vue2 第一节_Vue2上手_插值表达式{{}}_访问数据和修改数据_Vue开发者工具
文章目录 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染2. 插值表达式{{}}3. 访问数据和修改数据4. vue响应式5. Vue开发者工具--方便调试 1.Vue2上手-如何创建一个Vue实例,进行初始化渲染 准备容器引包创建Vue实例 new Vue()指定配置项 ->渲染数据 准备一个容器,例如: …...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

OCR MLLM Evaluation
为什么需要评测体系?——背景与矛盾 能干的事: 看清楚发票、身份证上的字(准确率>90%),速度飞快(眨眼间完成)。干不了的事: 碰到复杂表格(合并单元…...

flow_controllers
关键点: 流控制器类型: 同步(Sync):发布操作会阻塞,直到数据被确认发送。异步(Async):发布操作非阻塞,数据发送由后台线程处理。纯同步(PureSync…...
