【数据结构】归并排序、基数排序算法的学习知识点总结
目录
1、归并排序
1.1 算法思想
1.2 代码实现
1.3 例题分析
2、基数排序
2.1 算法思想
2.2 代码实现
2.3 例题分析
1、归并排序
1.1 算法思想
归并排序是一种采用分治思想的经典排序算法,通过将待排序数组分成若干个子序列,将每个子序列排序,最终合并成一个有序序列。其基本思路可以归纳为以下三个步骤:
- 分治:将待排序数组递归地分成两个子序列,直到每个子序列中只有一个元素;
- 合并:将两个有序子序列合并成一个有序序列,直到合并成一个完整的有序序列;
- 递归:重复以上两个步骤,直到排序完成。
具体实现过程中,可以采取自上而下或自下而上的方式进行归并排序。其中,自下而上的归并排序首先将整个数组划分成若干个大小为1的子数组,然后将相邻两个子数组合并成一个有序数组,逐渐扩大有序数组的长度,直到整个数组有序。
归并排序算法的时间复杂度为 O(nlogn),具有稳定性,适用于对大规模数据进行排序。
1.2 代码实现
归并排序(Merge Sort)是一种分治思想的排序算法,它的核心思想是将待排序的序列分成若干子序列,分别排序,然后合并。
C语言实现归并排序的代码如下:
#include <stdio.h>
#include <stdlib.h>void merge(int arr[], int l, int m, int r) {int i, j, k;int n1 = m - l + 1;int n2 = r - m;// 创建左右子数组int L[n1], R[n2];// 将数据复制到左右子数组中for (i = 0; i < n1; i++) {L[i] = arr[l + i];}for (j = 0; j < n2; j++) {R[j] = arr[m + 1 + j];}// 将左右子数组合并到 arr 中i = 0;j = 0;k = l;while (i < n1 && j < n2) {if (L[i] <= R[j]) {arr[k] = L[i];i++;} else {arr[k] = R[j];j++;}k++;}// 处理剩余元素while (i < n1) {arr[k] = L[i];i++;k++;}while (j < n2) {arr[k] = R[j];j++;k++;}
}void mergeSort(int arr[], int l, int r) {if (l < r) {int m = l + (r - l) / 2;// 分别对左右子数组进行排序mergeSort(arr, l, m);mergeSort(arr, m + 1, r);// 将左右子数组合并merge(arr, l, m, r);}
}int main() {int arr[] = {5, 1, 4, 2, 8, 0, 2};int n = sizeof(arr) / sizeof(arr[0]);printf("Original array: \n");for (int i = 0; i < n; i++) {printf("%d ", arr[i]);}// 执行归并排序mergeSort(arr, 0, n - 1);printf("\nSorted array: \n");for (int i = 0; i < n; i++) {printf("%d ", arr[i]);}return 0;
}
在这段代码中,merge() 函数用于合并左右子数组,mergeSort() 函数用于对左右子数组进行排序并合并。在 main() 函数中,我们创建了一个待排序的整数数组,然后调用 mergeSort() 函数对其进行排序,并输出排序后的结果。
1.3 例题分析
假设我们有一个无序数组[10, 5, 2, 7, 6, 4, 3, 8, 9, 1],要使用归并排序对其进行排序。下面是具体步骤:
1. 首先将数组不断分成两半,直到每个子数组只有一个元素为止。
[10, 5, 2, 7, 6, 4, 3, 8, 9, 1] -> [10, 5, 2, 7, 6] [4, 3, 8, 9, 1] -> [10, 5] [2, 7, 6] [4, 3] [8, 9, 1] -> [10] [5] [2] [7] [6] [4] [3] [8] [9] [1]
2. 接着,将相邻的两个子数组合并,并按顺序排序。
[10] [5] -> [5, 10]
[2] [7] [6] -> [2, 6, 7]
[4] [3] -> [3, 4]
[8] [9] [1] -> [1, 8, 9]
3. 重复步骤2,直到最终将所有子数组合并成为一个有序数组。
[5, 10] [2, 6, 7] [3, 4] [1, 8, 9] -> [2, 3, 4, 5, 6, 7, 8, 9, 10]
4. 最终得到的有序数组为[2, 3, 4, 5, 6, 7, 8, 9, 10]。可以看出,归并排序的时间复杂度为O(nlogn),且不会破坏原有数组的顺序。
2、基数排序
2.1 算法思想
基数排序是一种非比较排序算法,根据关键字的每一位来排序,最终得到有序序列。其基本思想是将待排序的元素按照其每一位的值,将其分配到对应的桶中,然后按照桶的顺序依次取出元素,即可得到有序序列。
具体实现步骤如下:
-
将所有待排序数按照个位数的值依次放入相应的桶中。
-
按照桶的顺序依次取出每个桶中的元素,将其按照一位数的大小依次放回原数组中。
-
对于十位数、百位数等同理,直到最高位数。
-
最终得到有序序列。
需要注意的是,基数排序算法的空间复杂度较高,需要额外的空间来存储桶和中间结果。在实际应用中,需要权衡算法的时间复杂度和空间复杂度,选择合适的算法。
2.2 代码实现
以下是一个基数排序的实现,它将一组数字按位数从低到高排序,每次排序都利用计数排序算法进行。
#include <iostream>
#include <vector>using namespace std;// 计数排序算法,用于将整数数组按某一位进行排序
void countingSort(vector<int>& arr, int exp)
{vector<int> output(arr.size());vector<int> count(10, 0);// 统计每个数字出现的次数for (int i = 0; i < arr.size(); i++)count[(arr[i] / exp) % 10]++;// 累加计数数组,求出每个数字在排序后的数组中的位置for (int i = 1; i < 10; i++)count[i] += count[i - 1];// 根据计数数组中的位置,将数字放置到排序后的数组中for (int i = arr.size() - 1; i >= 0; i--){output[count[(arr[i] / exp) % 10] - 1] = arr[i];count[(arr[i] / exp) % 10]--;}// 将排序后的数组复制到原始数组中for (int i = 0; i < arr.size(); i++)arr[i] = output[i];
}// 基数排序算法
void radixSort(vector<int>& arr)
{int max = *max_element(arr.begin(), arr.end());// 从低位到高位依次进行排序for (int exp = 1; max / exp > 0; exp *= 10)countingSort(arr, exp);
}int main()
{vector<int> arr = { 170, 45, 75, 90, 802, 24, 2, 66 };radixSort(arr);for (int i = 0; i < arr.size(); i++)cout << arr[i] << " ";return 0;
}
2.3 例题分析
基数排序是一种非比较排序算法,其基本思想是将待排序的数据按照位数划分为不同的数字位,然后依次对每一位进行排序。
例如,对于一个无序数组[753, 584, 626, 901, 321],经过一轮排序后,按照个位数字的大小,可以得到以下排列:[901, 321, 753, 584, 626],此时数组已经按照个位数字排好序了。
接下来,我们再按照十位数字的大小对这个序列进行排序,排完之后得到的序列为:[321, 584, 626, 901, 753]。
最后,再按照百位数字的大小进行排序就可以得到最终的有序数组:[321, 584, 626, 753, 901]。
基数排序的时间复杂度是O(d*(n+k)),其中d为位数,n为元素个数,k为数字范围。因此,当数字范围较小且位数不多时,基数排序的效率较高,但如果数字范围很大或者位数较多时,基数排序的效率就会下降。
相关文章:

【数据结构】归并排序、基数排序算法的学习知识点总结
目录 1、归并排序 1.1 算法思想 1.2 代码实现 1.3 例题分析 2、基数排序 2.1 算法思想 2.2 代码实现 2.3 例题分析 1、归并排序 1.1 算法思想 归并排序是一种采用分治思想的经典排序算法,通过将待排序数组分成若干个子序列,将每个子序列排序ÿ…...

【C++】C++模板进阶 —— 非类型模板参数、模板的特化以及模板的分离编译
📝个人主页:Sherry的成长之路 🏠学习社区:Sherry的成长之路(个人社区) 📖专栏链接:C学习 🎯长路漫漫浩浩,万事皆有期待 上一篇博客:【C】C多…...

HTML的相关知识
1.什么是HTML?基本语法 HTML: Hyper Text Markup Language (超文本标记语言) 超文本?超级文本,例如流媒体,声音、视频、图片等。 标记语言?这种语言是由大量的标签组成。HTML标签参考手…...

基于微信小程的流浪动物领养小程序设计与实现(源码+lw+部署文档+讲解等)
文章目录 前言系统主要功能:具体实现截图论文参考详细视频演示为什么选择我自己的网站自己的小程序(小蔡coding)有保障的售后福利 代码参考源码获取 前言 💗博主介绍:✌全网粉丝10W,CSDN特邀作者、博客专家、CSDN新星计…...

Java后端接口编写流程
💗wei_shuo的个人主页 💫wei_shuo的学习社区 🌐Hello World ! Java后端接口编写流程 Java后端接口编写流程,更具业务逻辑编写Java后端接口,提供给前端访问 实现逻辑流程 POJO:实体类编写 Data B…...
【问题记录】解决“命令行终端”和“Git Bash”操作本地Git仓库时出现 中文乱码 的问题!
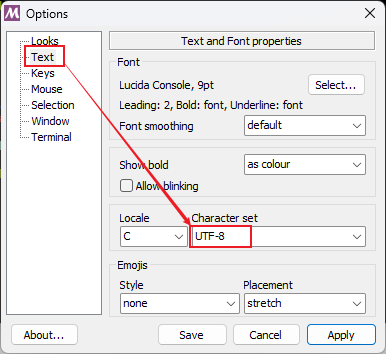
环境 Windows 11 家庭中文版git version 2.41.0.windows.1 问题情况 在使用 “命令行终端” 和 “Git Bash” 在本地Git仓库敲击命令时,对中文名称文件显示一连串的数字,如下所示:这种情况通常是由于字符编码设置不正确所引起的 解决办法 设置…...
软考高级之系统架构师之软件需求工程
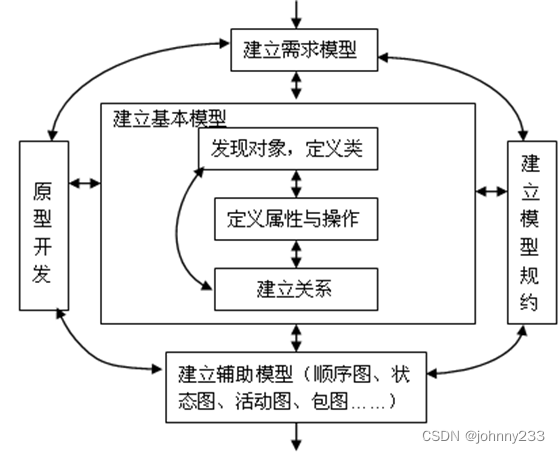
概述 一个完整的软件生存周期是以需求为出发点。软件需求是指用户对系统在功能、行为、性能、设计约束等方面的期望。 需求开发: 需求获取需求分析需求定义(需求规格说明书)需求验证 需求管理: 变更控制版本控制需求跟踪需求状态跟踪 需…...

使用 Velocity 模板引擎的 Spring Boot 应用
使用 Velocity 模板引擎的 Spring Boot 应用 模板引擎是构建动态内容的重要工具,特别适用于生成HTML、邮件内容、报告和其他文本文档。Velocity是一个强大的模板引擎,它具有简单易用的语法和灵活性。本文将介绍如何在Spring Boot应用中使用Velocity模板…...
mysql的mvcc详解
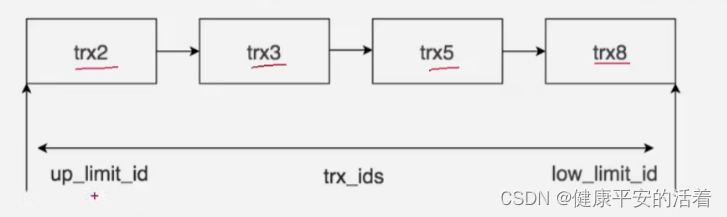
一 MVCC的作用 1.1 mvcc的作用 1.MVCC(Multiversion Concurrency Control)多版本并发控制。即通过数据行的多个版本管理来实现数据库的并发控制,使得在InnoDB事务隔离级别下执行一致性读操作有了保障。 2.mysql中的InnoDB中实现了MVCC主要…...

FreeRTOS两个死机原因(中断调用接口异常)【杂记】
1、中断回调函数中没有使用中断级API (xxFromISR) 函数 xSemaphoreGiveFromISR(uart_busy,&HighterTask);----正确 xSemaphoreGive(uart_busy);-----错误2、比configMAX_SYSCALL_INTERRUPT_PRIORITY优先级高的中断函数中使用了FreeRTOS的函数 3、临界代码保护后不可调用os…...
【AI视野·今日Robot 机器人论文速览 第四十三期】Thu, 28 Sep 2023
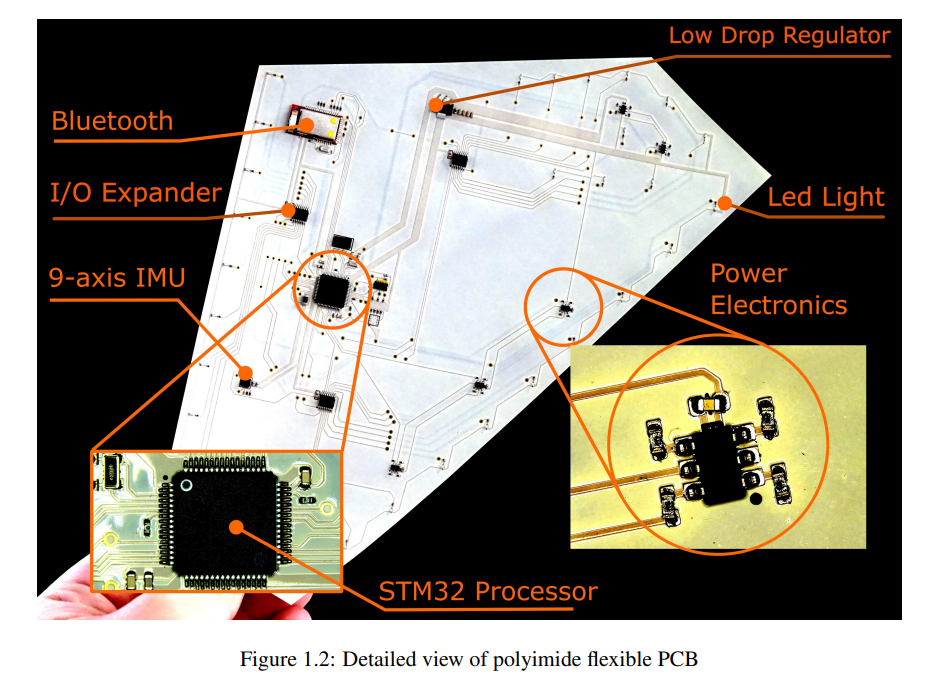
AI视野今日CS.Robotics 机器人学论文速览 Thu, 28 Sep 2023 Totally 37 papers 👉上期速览✈更多精彩请移步主页 Interesting: 📚****触觉力控学习策略,基于触觉的主动推理与力控用于小孔插入任务。提出了姿态控制与插入控制双策略模型。 (from 东京大学…...
批量快捷创建新数组的几种方式
1. for循环, push(比较简单, 就不上代码了) 2.创建空数组,填充null,然后map: function createData() { return new Array(1000) .fill(null) .map((v,i)>({name: name${i1}})) } console.log(createData()) 3.Array.frommap function createData() { return Array.from…...
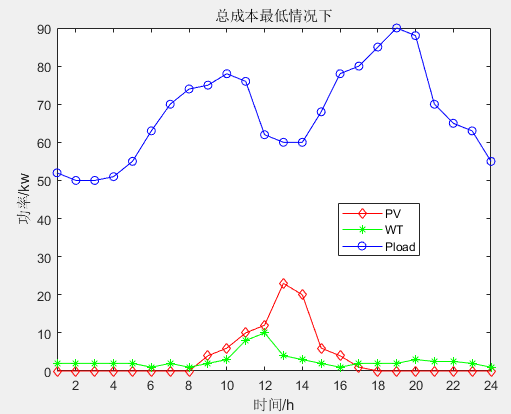
单目标应用:基于沙丁鱼优化算法(Sardine optimization algorithm,SOA)的微电网优化调度MATLAB
一、沙丁鱼优化算法 沙丁鱼优化算法(Sardine optimization algorithm,SOA)由Zhang HongGuang等人于2023年提出,该算法模拟沙丁鱼的生存策略,具有搜索能力强,求解精度高等特点。 沙丁鱼主要以浮游生物为食,这些生物包括细菌、腔肠…...

基于Halo搭建个人博客
准备 云服务器 安装Docker 开启8090端口 步骤 拉取Halo镜像 docker pull halohub/halo:2.1.0 制作容器并启动 docker run -it -d --name halo -p 8090:8090 -v ~/.halo2:/root/.halo2 halohub/halo:2.1.0 --halo.external-urlhttp://服务器ip:8090/ --halo.security.in…...

DPDK系列之三十一DPDK的并行机制简介
一、并行机制 什么是并行机制?这个很多开发者的眼中,其实是模糊的。可能说起来头头是道,但是细一查究竟,发现都是飘在空中的东西。在前面的“多核和多CPU编程”中,对并行机制已经进行了较深入的分析,这里只…...

【Java】复制数组的四种方式
1. System.arraycopy() 用来将一个数组的(一部分)内容复制到另一个数组里面去。 定义: void arraycopy(Object src, int srcPos, Object dest, int destPos, int length);例: int[] arr1 { 1, 2, 3, 4, 5 }; int[] arr2 new…...
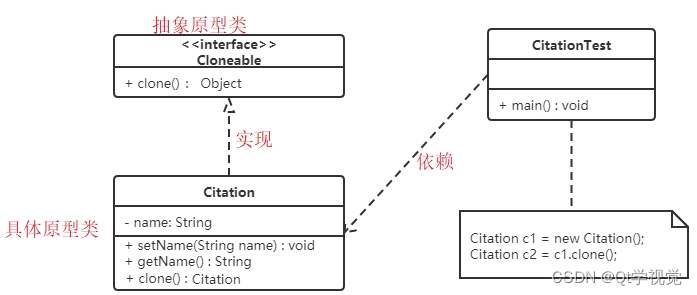
设计模式5、原型模式 Prototype
解释说明:使用原型实例指定待创建对象的类型,并且通过复制这个原型阿里创建型的对象 UML 结构图: 抽象原型(Prototype):规定了具体原型对象必须实现的clone()方法 具体原型(ConcretePrototype&…...

驱动挂载物理页代码示例
驱动挂载物理页代码示例 使用的实验环境为32位xp系统在101012分页模式下 此实验用于测试对分页模式的掌握程度 代码思路如下: 获取目标进程的cr3在目标进程中申请新的物理页拆分新申请的物理页的线性地址通过差分出的内容获取pte将pte写入到要挂载的线性地址的p…...

【新版】系统架构设计师 - 层次式架构设计理论与实践
个人总结,仅供参考,欢迎加好友一起讨论 文章目录 架构 - 层次式架构设计理论与实践考点摘要层次式体系结构概述表现层框架设计MVC模式MVP模式MVVM模式使用XML设计表现层表现层中UIP设计思想 中间层架构设计业务逻辑层工作流设计业务逻辑层设计 数据访问层…...

大数据Flink(九十):Lookup Join(维表 Join)
文章目录 Lookup Join(维表 Join) Lookup Join(维表 Join) Lookup Join 定义(支持 Batch\Streaming):Lookup Join 其实就是维表 Join,比如拿离线数仓来说,常常会有用户画像,设备画像等数据,而对应到实时数仓场景中,这种实时获取外部缓存的 Join 就叫做维表 Join。…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

基于uniapp+WebSocket实现聊天对话、消息监听、消息推送、聊天室等功能,多端兼容
基于 UniApp + WebSocket实现多端兼容的实时通讯系统,涵盖WebSocket连接建立、消息收发机制、多端兼容性配置、消息实时监听等功能,适配微信小程序、H5、Android、iOS等终端 目录 技术选型分析WebSocket协议优势UniApp跨平台特性WebSocket 基础实现连接管理消息收发连接…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来,实在找不到,希望有大佬教一下我。 还有就会议时间,我感觉不是图片时间,因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...
