【每日一题】2769. 找出最大的可达成数字
2769. 找出最大的可达成数字 - 力扣(LeetCode)
给你两个整数
num和t。如果整数
x可以在执行下述操作不超过t次的情况下变为与num相等,则称其为 可达成数字 :
- 每次操作将
x的值增加或减少1,同时可以选择将num的值增加或减少1。返回所有可达成数字中的最大值。可以证明至少存在一个可达成数字。
示例 1:
输入:num = 4, t = 1 输出:6 解释:最大可达成数字是 x = 6 ,执行下述操作可以使其等于 num : - x 减少 1 ,同时 num 增加 1 。此时,x = 5 且 num = 5 。 可以证明不存在大于 6 的可达成数字。示例 2:
输入:num = 3, t = 2 输出:7 解释:最大的可达成数字是 x = 7 ,执行下述操作可以使其等于 num : - x 减少 1 ,同时 num 增加 1 。此时,x = 6 且 num = 4 。 - x 减少 1 ,同时 num 增加 1 。此时,x = 5 且 num = 5 。 可以证明不存在大于 7 的可达成数字。提示:
1 <= num, t <= 50
class Solution {public int theMaximumAchievableX(int num, int t) {return num+2*t;}
}每日一题,今天是简单题。
开始之前,先祝大家中秋国庆双节快乐。国庆肯定是要回家玩啦!!!所以今天是一道简单题。
读题。可以发现要找到的是一个数x,经过t次操作之后,要和num相同。x可以是多个数,但要找到最大的那个x。所以,这里的操作一定是要用减的。但是呢,最后操作完的x又要跟num相等。对了,要注意,题目中说明了,num的加减操作和x的加减操作是可以在一次操作里完成的。所以实际上最大的x只有一个,num+2*t,也就是将num增加,x减少,直到t操作结束,那么x实际上就是num增加了t次,x减少了t次,num+t = x-t。所以x = num+2*t
运行,通过:
 最后,读万卷书,行万里路。国庆期间,大家也要行万里路呀。
最后,读万卷书,行万里路。国庆期间,大家也要行万里路呀。
相关文章:

【每日一题】2769. 找出最大的可达成数字
2769. 找出最大的可达成数字 - 力扣(LeetCode) 给你两个整数 num 和 t 。 如果整数 x 可以在执行下述操作不超过 t 次的情况下变为与 num 相等,则称其为 可达成数字 : 每次操作将 x 的值增加或减少 1 ,同时可以选择将 …...
开源电子合同签署平台小程序源码 在线签署电子合同小程序源码 合同在线签署源码
聚合市场上各类电子合同解决方案商,你无需一个一个的对接电子合同厂商, 费时,费力,因为这个工作我们已经做了适配,你只需要一个接口就能使用我们的所有服务商, 同时你还可以享受我们的接口渠道价格。 Mini-…...
36 二叉树中序遍历
二叉树中序遍历 题解1 递归题解2 迭代 给定一个二叉树的根节点 root ,返回它的 中序 遍历 。 提示: 树中节点数目在范围 [0, 100] 内-100 < Node.val < 100 进阶: 递归算法很简单,你可以通过迭代算法完成吗? 题解1 递归…...

广州华锐互动:VR结绳逃生训练模拟真实火灾场景,增强训练沉浸感
随着科技的发展,虚拟现实(VR)技术已被广泛应用到各个领域,其中包括消防训练。VR消防结绳训练是一种创新的消防训练方式,它通过虚拟现实技术模拟真实的灭火场景,使消防人员能够在无风险的环境中进行高强度的…...

Flink安装及简单使用
目录 转载处(个人用最新1.17.1测试) 依赖环境 安装包下载地址 Flink本地模式搭建 安装 启动集群 查看WebUI 停止集群 Flink Standalone搭建 安装 修改flink-conf.yaml配置文件 修改workers文件 复制Flink安装文件到其他服务器 启动集群 查…...

QT信号槽
目录 信号槽的概念 按钮的常用信号 自定义槽函数 自定义信号函数 自定义槽和信号注意的事项 信号与槽的拓展 lambda表达式 信号槽的概念 信号槽是Qt框架引以为豪的机制之一。所谓信号槽,实际就是观察者模式。当某个事件发生之后,比如,…...
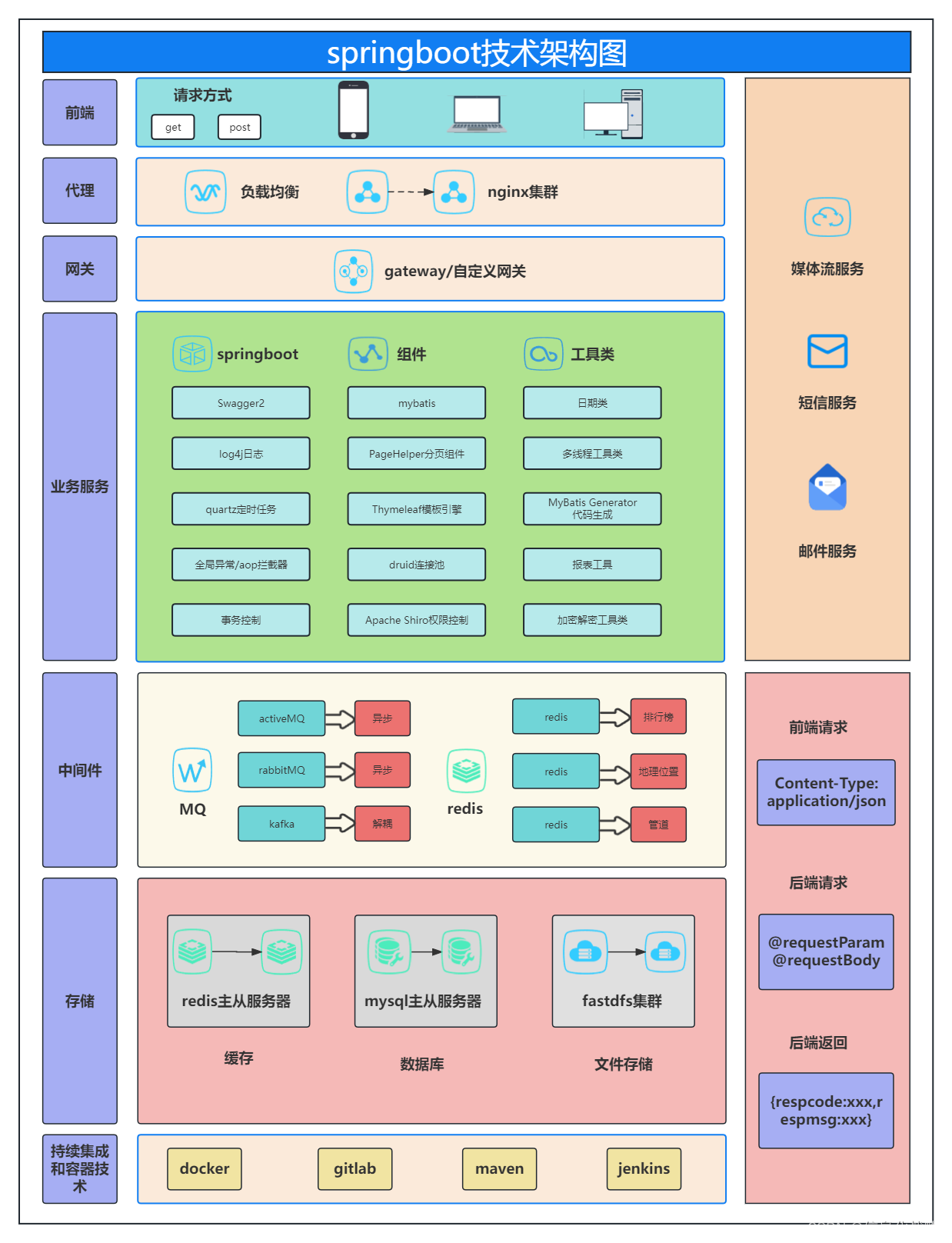
Spring Boot 技术架构图(InsCode AI 创作助手辅助)
Spring Boot 技术架构是一种用于构建现代应用程序的框架,它可以与各种前端、代理、网关、业务服务、中间件、存储、持续集成和容器服务集成在一起,以创建功能强大的应用程序。 源文件下载链接!!!!ÿ…...

python使用mitmproxy和mitmdump抓包在手机上抓包(三)
现在手机的使用率远超过电脑,所以这篇记录用mitmproxy抓手机包,实现手机流量监控。 环境:win10 64位,Python 3.10.4,雷电模拟器4.0.78,android版本7.1.2(设置-拉至最底部-关于平板电脑…...
react create-react-app v5 从零搭建(使用 npm run eject)
前言: 好久没用 create-react-app做项目了,这次为了个h5项目,就几个页面,决定自己搭建一个(ps:mmp 好久没用,搭建的时候遇到一堆问题)。 我之前都是使用 umi 。后台管理系统的项目 使用 antd-…...
在微信小程序中跳转到另一个小程序(多种实现方式)
方式一: 配置要跳转的appid和小程序页面路径 wx.navigateToMiniProgram({appId: 目标小程序appid,path: 目标小程序页面路径,//develop开发版;trial体验版;release正式版envVersion: release, success(res) {// 打开成功console.log("跳…...

beanstalkd 启动跟停止【经常使用 nohup 和 配合来启动程序,如: nohup ./test 同时免疫SIGINT和SIGHUP信号】
启动命令: nohup /usr/bin/beanstalkd -l 0.0.0.0 -p 11300 & >> /dev/null 2>&1 正常启动后,利用 【lsof -i:11300】查看 该服务是否正常启动 停止命令: /etc/init.d/beanstalkd stop 正常停止后,利用 【l…...
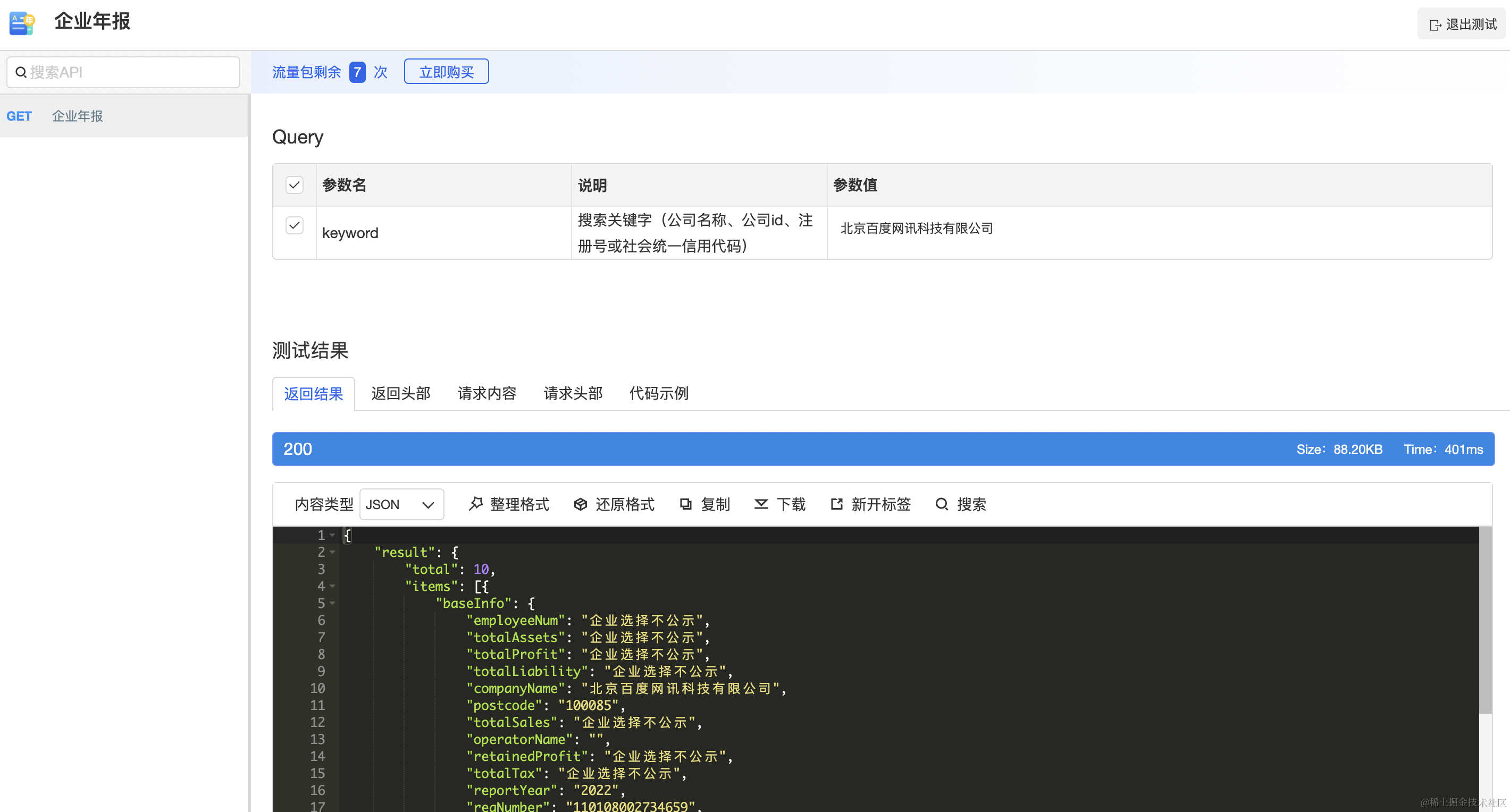
企业年报API的应用:从金融投资到市场研究
引言 在数字化时代,企业年报不再仅仅是一份财务报告,它们变成了宝贵的信息资源,可用于各种商业应用。企业年报API已经改变了金融投资和市场研究的方式,使得从中获取数据变得更加高效和灵活。本文将深入探讨企业年报API的应用&…...
)
基于Matlab实现评价型模型求解方法(附上源码+数据)
评价型模型求解方法是一种用于评估和比较不同方案或决策的方法。本文将介绍如何使用Matlab来实现评价型模型求解方法,并通过一个简单的案例研究来说明其应用。 文章目录 引言方法案例研究结果分析结论更多源码 引言 评价型模型求解方法在决策分析、风险评估和性能…...
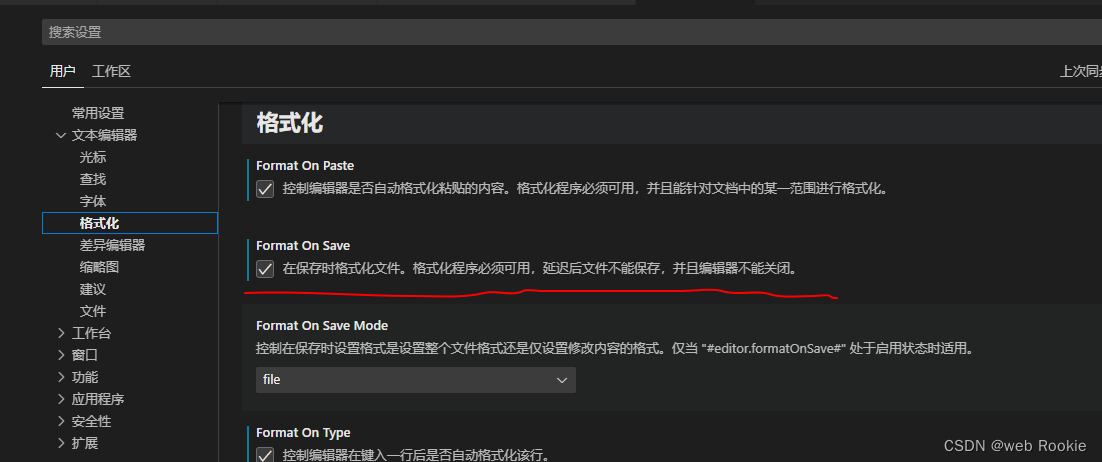
Prettier - Code formatter格式化规则文件
文章目录 前言安装使用 前言 先前公司在规范代码时,由于个人业务繁忙跟技术总监是后端出身用的IDEA不熟悉vsCode;以及大多数时都自己一个人负责一个项目,当时并不看重这些;最近在整理vue3tsvite的脚手架模板(平时工作用的react),开始整理格式化代码,方便之后 vue 和 react 中应…...

用C++实现文件读写操作
文件读写操作是C编程中非常常见的操作之一。下面是一个简单的示例,演示如何使用C读取和写入文件。 读取文件: #include <iostream> #include <fstream>int main() {std::ifstream inputFile("input.txt");if (!inputFile) {std:…...
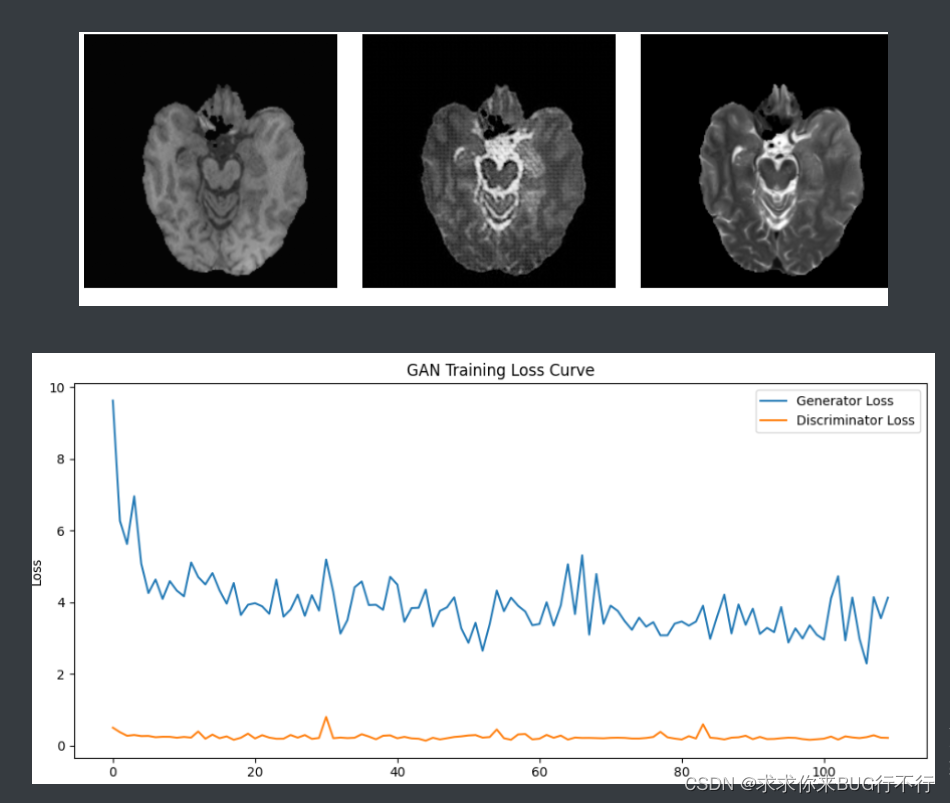
【我的创作纪念日】使用pix2pixgan实现barts2020数据集的处理(完整版本)
使用pix2pixgan (pytorch)实现T1 -> T2的基本代码 使用 https://github.com/eriklindernoren/PyTorch-GAN/ 这里面的pix2pixgan代码进行实现。 进去之后我们需要重新处理数据集,并且源代码里面先训练的生成器,后训练鉴别器。 一般情况下…...
)
背包算法(Knapsack problem)
背包算法(Knapsack problem)是一种常见的动态规划问题,它的基本思想是利用动态规划思想求解给定重量和价值下的最优解。具体来说,背包算法用于解决一个整数背包问题,即给定一组物品,每个物品有自己的重量和…...

“童”趣迎国庆 安全“童”行-柿铺梁坡社区开展迎国庆活动
“金秋十月好心境,举国欢腾迎国庆。”国庆节来临之际,为进一步加强梁坡社区未成年人爱国主义教育,丰富文化生活,营造热烈喜庆、文明和谐的节日氛围。9月24日上午,樊城区柿铺街道梁坡社区新时代文明实践站联合襄阳市和时…...

常用压缩解压缩命令
在Linux中常见的压缩格式有.zip、.rar、.tar.gz.、tar.bz2等压缩格式。不同的压缩格式需要用不同的压缩命令和工具。须知,在Linux系统中.tar.gz为标准格式的压缩和解压缩格式,因此本文也会着重讲解tar.gz格式压缩包的压缩和解压缩命令。须知,…...

第四十一章 持久对象和SQL - Storage
文章目录 第四十一章 持久对象和SQL - StorageStorage存储定义概览持久类使用的Globals注意 第四十一章 持久对象和SQL - Storage Storage 每个持久类定义都包含描述类属性如何映射到实际存储它们的Global的信息。类编译器为类生成此信息,并在修改和重新编译时更新…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

手机平板能效生态设计指令EU 2023/1670标准解读
手机平板能效生态设计指令EU 2023/1670标准解读 以下是针对欧盟《手机和平板电脑生态设计法规》(EU) 2023/1670 的核心解读,综合法规核心要求、最新修正及企业合规要点: 一、法规背景与目标 生效与强制时间 发布于2023年8月31日(OJ公报&…...

适应性Java用于现代 API:REST、GraphQL 和事件驱动
在快速发展的软件开发领域,REST、GraphQL 和事件驱动架构等新的 API 标准对于构建可扩展、高效的系统至关重要。Java 在现代 API 方面以其在企业应用中的稳定性而闻名,不断适应这些现代范式的需求。随着不断发展的生态系统,Java 在现代 API 方…...
