洛谷题解 | AT_abc321_c Primes on Interval
目录
- 题目翻译
- 题目描述
- 输入格式
- 输出格式
- 样例 #1
- 样例输入 #1
- 样例输出 #1
- 样例 #2
- 样例输入 #2
- 样例输出 #2
- 样例 #3
- 样例输入 #3
- 样例输出 #3
- 题目简化
- 题目思路
- AC代码
题目翻译
【题目描述】
你决定用素数定理来做一个调查. 众所周知, 素数又被称为质数,其含义就是除了数字一和本身之外不能被其他任何的数字除尽.
现在给定一个正整数序列 a , a + 1 , ⋯ , b a,a+1,\cdots,b a,a+1,⋯,b ( a ≤ b ) (a \le b) (a≤b), 请找出一个最小值 l l l, 使其满足对于任意一个长度为 l l l 的子串, 都包含 k k k 个质数.
找到并输出符合要求的最小值 l l l, 如果不存在符合要求的长度 l l l, 则输出 − 1 -1 −1.
【输入格式】
输入一行, 包含三个用空格隔开的整数 a , b , k a,b,k a,b,k ( 1 ≤ a , b , k ≤ 1 0 6 ; a ≤ b 1 \le a,b,k \le 10^{6}; a \le b 1≤a,b,k≤106;a≤b)
【输出格式】
输出一行, 为符合要求的最小值 l l l, 若不存在, 输出 − 1 -1 −1.
题目描述
You’ve decided to carry out a survey in the theory of prime numbers. Let us remind you that a prime number is a positive integer that has exactly two distinct positive integer divisors.
Consider positive integers $ a $ , $ a+1 $ , $ … $ , $ b $ $ (a<=b) $ . You want to find the minimum integer $ l $ $ (1<=l<=b-a+1) $ such that for any integer $ x $ $ (a<=x<=b-l+1) $ among $ l $ integers $ x $ , $ x+1 $ , $ … $ , $ x+l-1 $ there are at least $ k $ prime numbers.
Find and print the required minimum $ l $ . If no value $ l $ meets the described limitations, print -1.
输入格式
A single line contains three space-separated integers $ a,b,k $ ( $ 1<=a,b,k<=10^{6}; a<=b $ ).
输出格式
In a single line print a single integer — the required minimum $ l $ . If there’s no solution, print -1.
样例 #1
样例输入 #1
2 4 2
样例输出 #1
3
样例 #2
样例输入 #2
6 13 1
样例输出 #2
4
样例 #3
样例输入 #3
1 4 3
样例输出 #3
-1
题目简化
求一个区间内,任意长度为 l l l 的子串中都包含 k k k 个质数的最小 l l l。
题目思路
初始化一个数组存储从 2 2 2 开始的所有素数。初始化后,这个数组中所有值都是 true,表示对应的数是素数。
使用埃拉托斯特尼筛法(Sieve of Eratosthenes)来找出所有小于 M A X MAX MAX 的素数。这个算法的主要思想是,如果一个数不是素数,那么它必定有一个因子小于或等于其平方根。因此,我们只需要检查到每个数的平方根即可。
在主循环中,读取三个输入: a a a, b b b 和 k k k。然后,创建一个队列 q q q 并把 a − 1 a-1 a−1 放入队列。
接下来,进行一系列操作来找出在区间 [ a , b ] \text [a, b] [a,b] 中,长度为 k k k 的所有素数子序列。如果存在这样的子序列,那么就更新 r e s res res 的值。
如果 q q q 的头部元素是 a − 1 a-1 a−1,那么就输出 -1 \texttt -\texttt 1 -1,否则输出 r e s res res。
AC代码
#include <bits/stdc++.h>
using namespace std;
#define li long long int
#define rep(i,to) for(li i=0;i<((li)(to));++i)
#define pb push_back
#define sz(v) ((li)(v).size())
#define bit(n) (1ll<<(li)(n))
#define all(vec) (vec).begin(),(vec).end()
#define each(i,c) for(__typeof((c).begin()) i=(c).begin();i!=(c).end();i++)
#define MP make_pair
#define F first
#define S second#define MAX 1000500
li is_prime[MAX];int main()
{rep(i, MAX)if(2 <= i) is_prime[i] = true;for(li i = 2; i * i < MAX; i++){if(!is_prime[i]) continue;for(li j = i * i; j < MAX; j += i) is_prime[j] = false;}li a, b, k;cin >> a >> b >> k;queue<li> q;li res = -1;q.push(a - 1);for(li pos = a; pos <= b; pos++){if(is_prime[pos]) q.push(pos);while(k < sz(q)) q.pop();if(sz(q) == k) res = max(res, pos - q.front() + 1);}if(q.front() == a - 1) cout << -1 << endl;else cout << res << endl;
}
创作不易,白嫖不好,各位的支持和认可,就是我创作的最大动力,如果喜欢我的文章,给个关注吧!
冰焰狼 | 文
如果本篇博客有任何错误,请批评指教,不胜感激 !
相关文章:

洛谷题解 | AT_abc321_c Primes on Interval
目录 题目翻译题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1 样例 #2样例输入 #2样例输出 #2 样例 #3样例输入 #3样例输出 #3 题目简化题目思路AC代码 题目翻译 【题目描述】 你决定用素数定理来做一个调查. 众所周知, 素数又被称为质数,其含义就是除了数…...
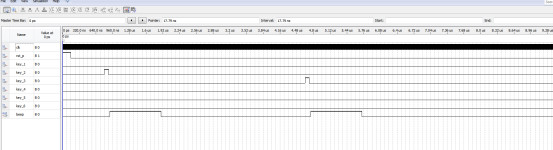
Quartus医院病房呼叫系统病床呼叫Verilog,源代码下载
名称:医院病房呼叫系统病床呼叫 软件:Quartus 语言:Verilog 要求: 1、用1~6个开关模拟6个病房的呼叫输入信号,1号优先级最高;1~6优先级依次降低; 2、 用一个数码管显示呼叫信号的号码;没信号呼叫时显示0;有多个信号呼叫时,显…...
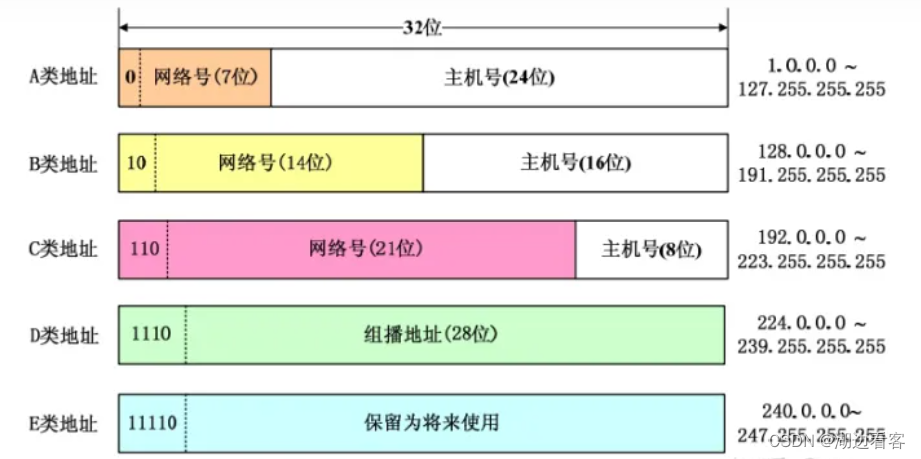
ip的标准分类---分类的Ip
分类的 IP 即将 IP 地址划分为若干个固定类,每一类地址都由两个固定长度的字段组成。 其中第一个字段是网络号(net-id),它标志主机或路由器所连接的网络。一个网络号在整个因特网内必须是唯一的。 第二个字段是主机号…...
)
理解并掌握C#的Channel:从使用案例到源码解读(一)
引言 在C#的并发编程中,Channel是一种非常强大的数据结构,用于在生产者和消费者之间进行通信。本文将首先通过一个实际的使用案例,介绍如何在C#中使用Channel,然后深入到Channel的源码中,解析其内部的实现机制。 使用案…...

如何让git命令仅针对当前目录
背景 我们有时候建的git仓库是这样的,a目录下有b、c、d三个模块(文件夹)。有时候只想查看b下面的变化,而使用 git status、git diff 的时候会把c和d的变化都列出来,要怎么只查b目录的变化? 操作 要查b目…...

【0223】源码剖析smgr底层设计机制(3)
1. smgr设计机制 PG内核中smgr完整磁盘存储介质的管理是通过下面三部分实现的。 1.1 函数指针结构体 f_smgr 函数指针结构体 f_smgr。 通过该函数指针类型,可完成类似于UNIX系统中的VFD功能,上层只需要调用open()、read()、write()等系统函数,用户不必去关系底层的文件系统…...

Visual Studio 2019 C# winform CefSharp 中播放视频及全屏播放
VS C# winform CefSharp 浏览器控件,默认不支持视频播放,好在有大佬魔改了dll,支持流媒体视频播放。虽然找了很久,好歹还是找到了一个版本100.0.230的dll(资源放在文末) 首先创建一个项目 第二、引入CefSha…...

天选之子Linux是如何发展起来的?为何对全球IT行业的影响如此之大?
天选之子Linux是如何发展起来的?为何对全球IT行业的影响如此之大? 前言一、UNIX发展史二、Linux发展历史三、开源四、官网五、 企业应用现状六、发行版本 前言 上面这副图是博主历时半小时完成的,给出了Linxu的一些发展背景。球球给位看官老…...
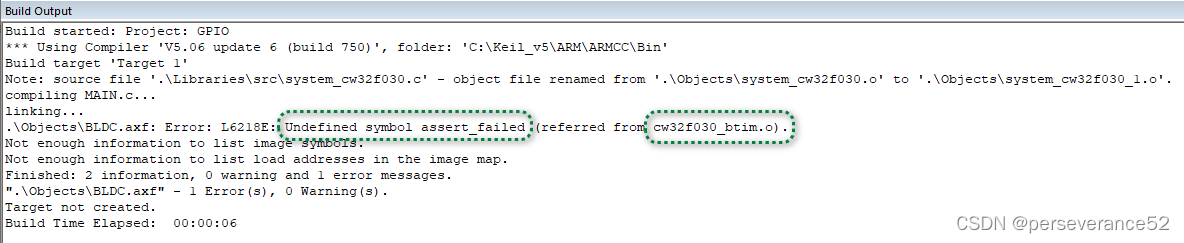
MDK报错:Undefined symbol assert_failed报错解决策略
MDK报错:Undefined symbol assert_failed报错解决策略 🎯🪕在全网搜索相关MDK编译报错:Error: L6218E: Undefined symbol assert_param (referred from xxx.o). ✨有些问题看似很简单,可能产生的问题是由于不经意的细节原因导致。…...
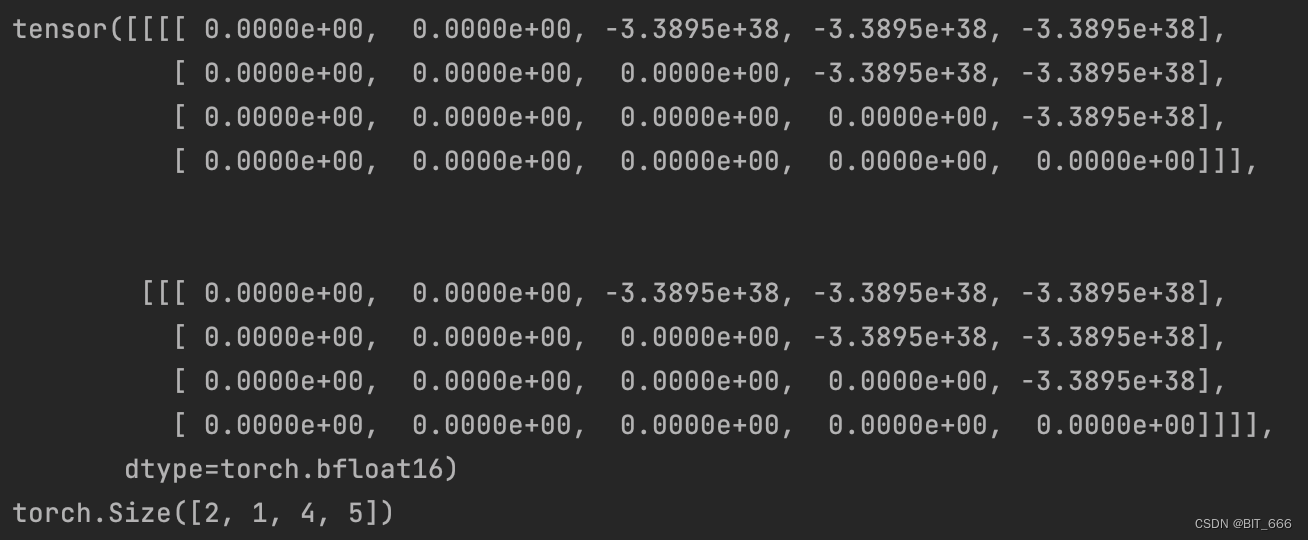
LLM - Make Causal Mask 构造因果关系掩码
目录 一.引言 二.make_causal_mask 1.完整代码 2.Torch.full 3.torch.view 4.torch.masked_fill_ 5.past_key_values_length 6.Test Main 三.总结 一.引言 Causal Mask 主要用于限定模型的可视范围,防止模型看到未来的数据。在具体应用中,Caus…...
概念和itertools)
Python函数式编程(一)概念和itertools
Python函数式编程是一种编程范式,它强调使用纯函数来处理数据。函数是程序的基本构建块,并且尽可能避免或最小化可变状态和副作用。在函数式编程中,函数被视为一等公民,可以像值一样传递和存储。 函数式编程概念 编程语言支持通…...
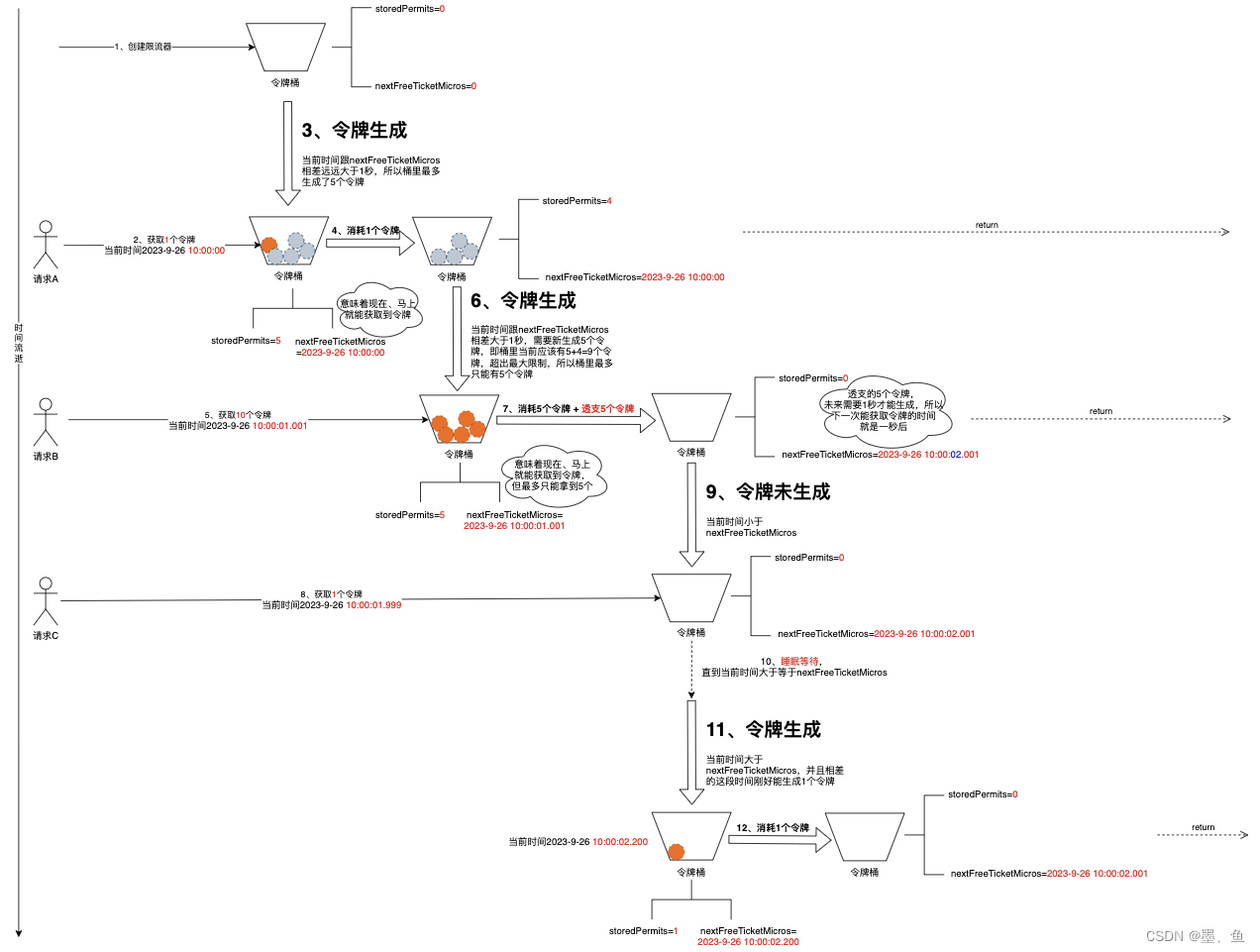
Guava限流器原理浅析
文章目录 基本知识限流器的类图使用示例 原理解析限流整体流程问题驱动1、限流器创建的时候会初始化令牌吗?2、令牌是如何放到桶里的?3、如果要获取的令牌数大于桶里的令牌数会怎么样4、令牌数量的更新会有并发问题吗 总结 实际工作中难免有限流的场景。…...

第四十二章 持久对象和SQL - 用于创建持久类和表的选项
文章目录 第四十二章 持久对象和SQL - 用于创建持久类和表的选项用于创建持久类和表的选项访问数据 第四十二章 持久对象和SQL - 用于创建持久类和表的选项 用于创建持久类和表的选项 要创建持久类及其对应的 SQL 表,可以执行以下任一操作: 使用 IDE …...

集合-ArrayList源码分析(面试)
系列文章目录 1.集合-Collection-CSDN博客 2.集合-List集合-CSDN博客 3.集合-ArrayList源码分析(面试)_喜欢吃animal milk的博客-CSDN博客 目录 系列文章目录 前言 一 . 什么是ArrayList? 二 . ArrayList集合底层原理 总结 前言 大家好,今天给大家讲一下Arra…...
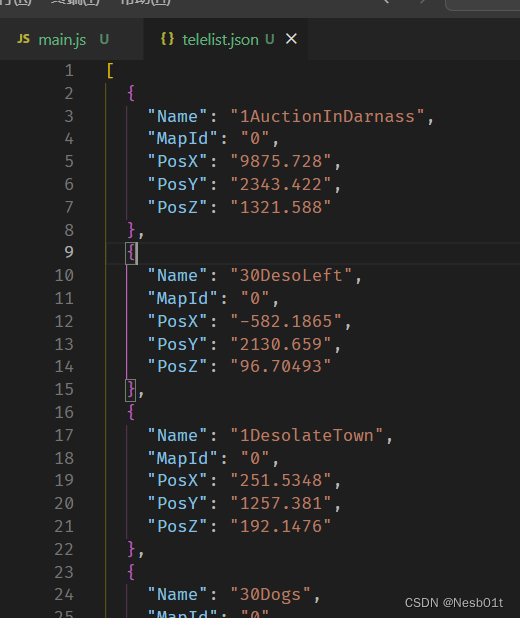
跨类型文本文件,反序列化与类型转换的思考
文章目录 应用场景序列化 - 对象替换原内容,方便使用编写程序取得结果数组 序列化 - JSON 应用场景 在编写热更新的时候,我发现了一个古早的 ini 文件,记录了许多有用的数据 由于使用的语言年份较新,没有办法较好地对 ini 文件的…...
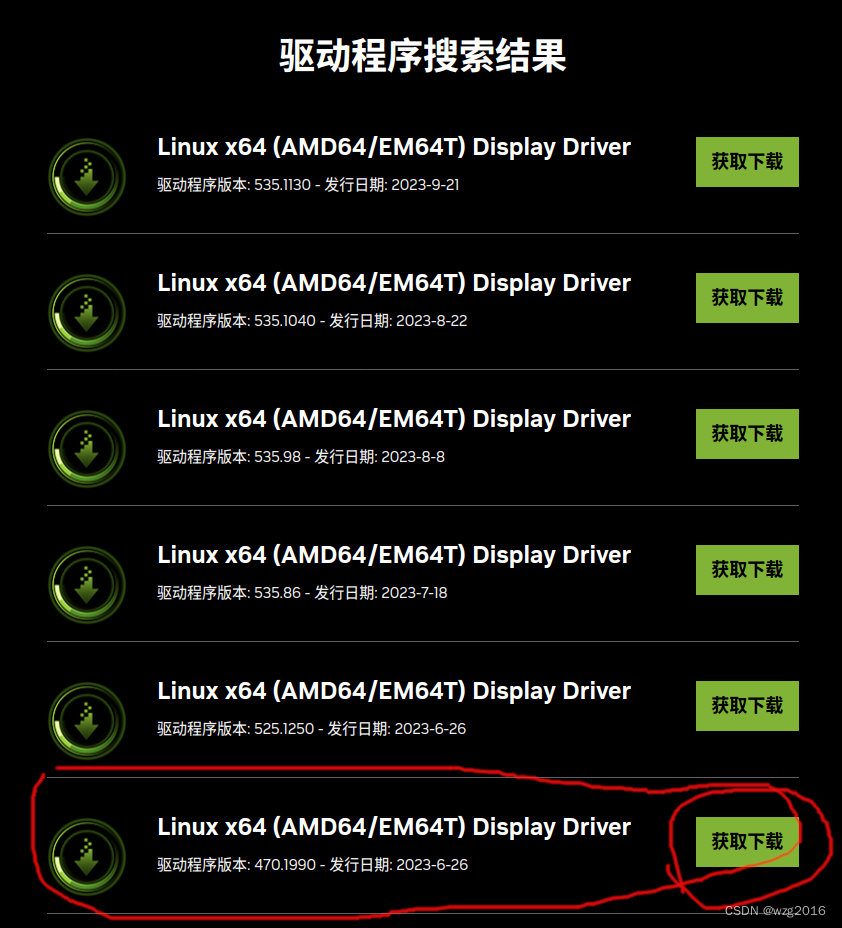
ubuntu20安装nvidia驱动
1. 查看显卡型号 lspci | grep -i nvidia 我的输出: 01:00.0 VGA compatible controller: NVIDIA Corporation GP104 [GeForce GTX 1080] (rev a1) 01:00.1 Audio device: NVIDIA Corporation GP104 High Definition Audio Controller (rev a1) 07:00.0 VGA comp…...

gma 2 成书计划
随着 gma 2 整体构建完成。下一步计划针对库内所有功能完成一个用户指南(非网站)。 封皮 主要章节 章节完成度相关链接第 1 章 GMA 概述已完成第 2 章 地理空间数据操作已完成第 3 章 坐标参考系统已完成第 4 章 地理空间制图已完成第 5 章 数学运算模…...
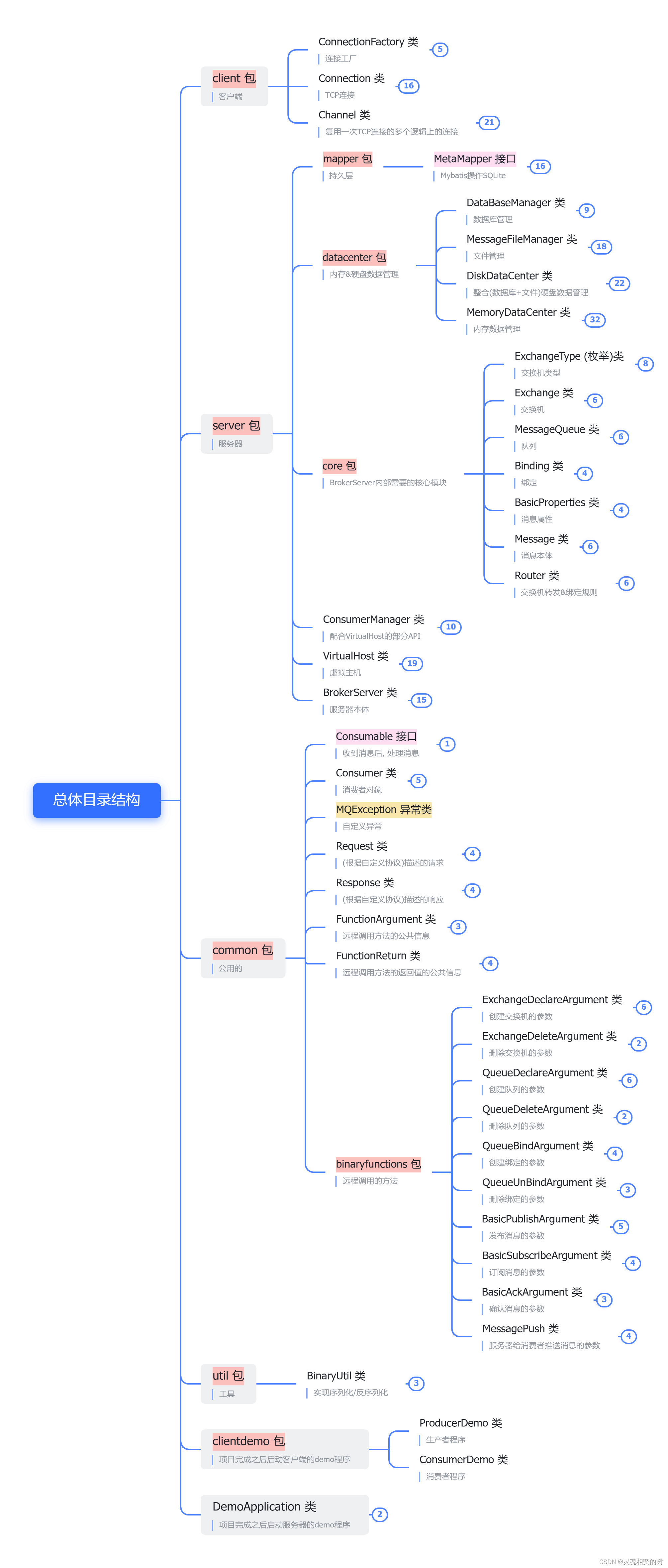
从零手搓一个【消息队列】项目设计、需求分析、模块划分、目录结构
文章目录 一、需求分析1, 项目简介2, BrokerServer 核心概念3, BrokerServer 提供的核心 API4, 交换机类型5, 持久化存储6, 网络通信7, TCP 连接的复用8, 需求分析小结 二、模块划分三、目录结构 提示:是正在努力进步的小菜鸟一只,如有大佬发现文章欠佳之…...

【Spring Cloud】深入探索 Nacos 注册中心的原理,服务的注册与发现,服务分层模型,负载均衡策略,微服务的权重设置,环境隔离
文章目录 前言一、初识 Nacos 注册中心1.1 什么是 Nacos1.2 Nacos 的安装,配置,启动 二、服务的注册与发现三、Nacos 服务分层模型3.1 Nacos 的服务分级存储模型3.2 服务跨集群调用问题3.3 服务集群属性设置3.4 修改负载均衡策略为集群策略 四、根据服务…...

No156.精选前端面试题,享受每天的挑战和学习
🤍 前端开发工程师(主业)、技术博主(副业)、已过CET6 🍨 阿珊和她的猫_CSDN个人主页 🕠 牛客高级专题作者、在牛客打造高质量专栏《前端面试必备》 🍚 蓝桥云课签约作者、已在蓝桥云课上架的前后端实战课程《Vue.js 和 Egg.js 开发企业级健康管理项目》、《带你从入…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

算法岗面试经验分享-大模型篇
文章目录 A 基础语言模型A.1 TransformerA.2 Bert B 大语言模型结构B.1 GPTB.2 LLamaB.3 ChatGLMB.4 Qwen C 大语言模型微调C.1 Fine-tuningC.2 Adapter-tuningC.3 Prefix-tuningC.4 P-tuningC.5 LoRA A 基础语言模型 A.1 Transformer (1)资源 论文&a…...

JVM 内存结构 详解
内存结构 运行时数据区: Java虚拟机在运行Java程序过程中管理的内存区域。 程序计数器: 线程私有,程序控制流的指示器,分支、循环、跳转、异常处理、线程恢复等基础功能都依赖这个计数器完成。 每个线程都有一个程序计数…...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...

GraphQL 实战篇:Apollo Client 配置与缓存
GraphQL 实战篇:Apollo Client 配置与缓存 上一篇:GraphQL 入门篇:基础查询语法 依旧和上一篇的笔记一样,主实操,没啥过多的细节讲解,代码具体在: https://github.com/GoldenaArcher/graphql…...

xmind转换为markdown
文章目录 解锁思维导图新姿势:将XMind转为结构化Markdown 一、认识Xmind结构二、核心转换流程详解1.解压XMind文件(ZIP处理)2.解析JSON数据结构3:递归转换树形结构4:Markdown层级生成逻辑 三、完整代码 解锁思维导图新…...

WEB3全栈开发——面试专业技能点P7前端与链上集成
一、Next.js技术栈 ✅ 概念介绍 Next.js 是一个基于 React 的 服务端渲染(SSR)与静态网站生成(SSG) 框架,由 Vercel 开发。它简化了构建生产级 React 应用的过程,并内置了很多特性: ✅ 文件系…...

篇章二 论坛系统——系统设计
目录 2.系统设计 2.1 技术选型 2.2 设计数据库结构 2.2.1 数据库实体 1. 数据库设计 1.1 数据库名: forum db 1.2 表的设计 1.3 编写SQL 2.系统设计 2.1 技术选型 2.2 设计数据库结构 2.2.1 数据库实体 通过需求分析获得概念类并结合业务实现过程中的技术需要&#x…...
