幂级数和幂级数的和函数有什么关系?
幂级数和幂级数的和函数有什么关系?
本文例子引用自:80_1幂级数运算,逐项积分、求导【小元老师】高等数学,考研数学
求幂级数 ∑ n = 1 ∞ 1 n x n \sum\limits_{n=1}^{\infty}\frac{1}{n}x^n n=1∑∞n1xn 的和函数
(1)求收敛半径,由于是不缺项级数所以可以使用 lim n → ∞ ∣ a n + 1 a n ∣ = ρ \lim\limits_{n\rightarrow\infty}|\frac{a_{n+1}}{a_n}|=\rho n→∞lim∣anan+1∣=ρ,若是缺项级数则只能使用 lim n → ∞ ∣ u n + 1 ( x ) u n ( x ) ∣ = ρ ∣ ϕ ( x ) ∣ < 1 \lim\limits_{n\rightarrow\infty}|\frac{u_{n+1}(x)}{u_n(x)}|=\rho|\phi(x)|\lt 1 n→∞lim∣un(x)un+1(x)∣=ρ∣ϕ(x)∣<1,当然不缺项级数也可使用后者。
ρ = lim n → ∞ ∣ a n + 1 a n ∣ = lim n → ∞ ∣ 1 n + 1 1 n ∣ = 1 \rho=\lim\limits_{n\rightarrow\infty}|\frac{a_{n+1}}{a_n}|=\lim\limits_{n\rightarrow\infty}|\frac{\frac{1}{n+1}}{\frac{1}{n}}|=1 ρ=n→∞lim∣anan+1∣=n→∞lim∣n1n+11∣=1
(2)判断端点处的敛散性
当 x = − 1 x=-1 x=−1 时, ∑ n = 1 ∞ ( − 1 ) n 1 n \sum\limits_{n=1}^{\infty}(-1)^n\frac{1}{n} n=1∑∞(−1)nn1, u n = 1 n → 0 u_n=\frac{1}{n}\rightarrow0 un=n1→0 且 u n = 1 n u_n=\frac{1}{n} un=n1递减,级数收敛(利用交错级数的莱布尼茨定理判别)
当 x = 1 x=1 x=1 时, ∑ n = 1 ∞ 1 n \sum\limits_{n=1}^{\infty}\frac{1}{n} n=1∑∞n1, p = 1 p=1 p=1,级数发散(利用p级数判别)
(3)综上,该级数收敛域 [ − 1 , 1 ) [-1,1) [−1,1)
(4)求收敛域中幂级数的和函数(在收敛域中幂级数等于其和函数,超过收敛域二者不等)
s ( x ) = ∑ n = 1 ∞ 1 n x n = x + 1 2 x 2 + 1 3 x 3 + ⋯ + 1 n x n + ⋯ s(x)=\sum\limits_{n=1}^{\infty}\frac{1}{n}x^n=x+\frac{1}{2}x^2+\frac{1}{3}x^3+\cdots+\frac{1}{n}x^n+\cdots s(x)=n=1∑∞n1xn=x+21x2+31x3+⋯+n1xn+⋯
逐项求导
s ′ ( x ) = ( ∑ n = 1 ∞ 1 n x n ) ′ = 1 + x + x 2 + ⋯ + 1 n x n − 1 + ⋯ = 1 1 − x s'(x)=\big(\sum\limits_{n=1}^{\infty}\frac{1}{n}x^n\big)'=1+x+x^2+\cdots+\frac{1}{n}x^{n-1}+\cdots=\frac{1}{1-x} s′(x)=(n=1∑∞n1xn)′=1+x+x2+⋯+n1xn−1+⋯=1−x1
左右两端同时积分(右侧逐项积分)
s ( x ) = s ( 0 ) + ∫ 0 x s ′ ( t ) d t = 0 + ∫ 0 x 1 1 − t d t = − ln ( 1 − x ) s(x)=s(0)+\int_0^xs'(t)dt=0+\int_0^x\frac{1}{1-t}dt=-\ln(1-x) s(x)=s(0)+∫0xs′(t)dt=0+∫0x1−t1dt=−ln(1−x)
上式为什么还有 s ( 0 ) s(0) s(0)?
∫ 0 x s ′ ( t ) d t = s ( x ) ∣ 0 x = s ( x ) − s ( 0 ) s ( x ) = s ( 0 ) + ∫ 0 x s ′ ( t ) d t \int_0^xs'(t)dt=s(x)|_0^x=s(x)-s(0)\\ ~\\ s(x)=s(0)+\int_0^xs'(t)dt ∫0xs′(t)dt=s(x)∣0x=s(x)−s(0) s(x)=s(0)+∫0xs′(t)dt
最终收敛域上幂级数的和函数为:
s ( x ) = − ln ( 1 − x ) , x ∈ [ − 1 , 1 ) s(x)=-\ln(1-x),x\in[-1,1) s(x)=−ln(1−x),x∈[−1,1)
我们为什么要兜圈子先对级数求导(或积分)然后再进行积分(或求导)呢?
主要想利用等比级数,因为其和函数容易求得,而逐项求导和积分的目的是将所给幂级数变换为等比级数,随后利用等比级数求出所给幂级数的和函数

我们在图像中看看到底幂级数和幂级数的和函数有什么关系?
下图中幂级数的图像为绿色曲线,其实不是真正的图像,因为 n n n为无穷大,笔者这里 n n n只取到了9,仅做示意。下图中红色曲线为幂级数和函数的图像,我们可以发现在收敛域中幂级数等于其和函数,超过收敛域二者是不等的

相关文章:

幂级数和幂级数的和函数有什么关系?
幂级数和幂级数的和函数有什么关系? 本文例子引用自:80_1幂级数运算,逐项积分、求导【小元老师】高等数学,考研数学 求幂级数 ∑ n 1 ∞ 1 n x n \sum\limits_{n1}^{\infty}\frac{1}{n}x^n n1∑∞n1xn 的和函数 ÿ…...

Git多账号管理通过ssh 公钥的方式,git,gitlab,gitee
按照目前国内访问git,如果不科学上网,我们很大可能访问会超时。基于这个,所以我现在的git 配置已经增加到了3个了 一个公司gitlab,一个git,一个gitee. 以下基于这个环境,我们来说明下如何创建配置ssh公钥。…...

在nodejs常见的不良做法及其优化解决方案
在nodejs常见的不良做法及其优化解决方案 当涉及到在express和nodejs中开发应用程序时。遵循最佳实践对于确保项目的健壮性、可维护性和安全性至关重要。 在本文中,我们将探索开发人员经常遇到的几种常见的错误做法,并通过代码示例研究优化的最佳做法&…...

关于layui upload上传组件上传文件无反应的问题
最近使用layui upload组件时,碰到了上传文件无反应的问题,感到非常困惑。 因为使用layui upload组件不是一次两次了,之前每次都可以,这次使用同样的配方,同样的姿势,为什么就不行了呢? 照例先…...

容器网络之Flannel
第一个问题位置变化,往往是通过一个称为注册中心的地方统一管理的,这个是应用自己做的。当一个应用启动的时候,将自己所在环境的 IP 地址和端口,注册到注册中心指挥部,这样其他的应用请求它的时候,到指挥…...
:如何进行乳腺癌检测?)
SVM(下):如何进行乳腺癌检测?
⭐️⭐️⭐️⭐️⭐️欢迎来到我的博客⭐️⭐️⭐️⭐️⭐️ 🐴作者:秋无之地 🐴简介:CSDN爬虫、后端、大数据领域创作者。目前从事python爬虫、后端和大数据等相关工作,主要擅长领域有:爬虫、后端、大数据开发、数据分析等。 🐴欢迎小伙伴们点赞👍🏻、收藏⭐️、…...

嵌入式Linux应用开发-第十五章具体单板的按键驱动程序
嵌入式Linux应用开发-第十五章具体单板的按键驱动程序 第十五章 具体单板的按键驱动程序(查询方式)15.1 GPIO操作回顾15.2 AM335X的按键驱动程序(查询方式)15.2.1 先看原理图确定引脚及操作方法15.2.2 再看芯片手册确定寄存器及操作方法15.2.3 编程15.2.3.1 程序框架15.2.3.2 硬…...
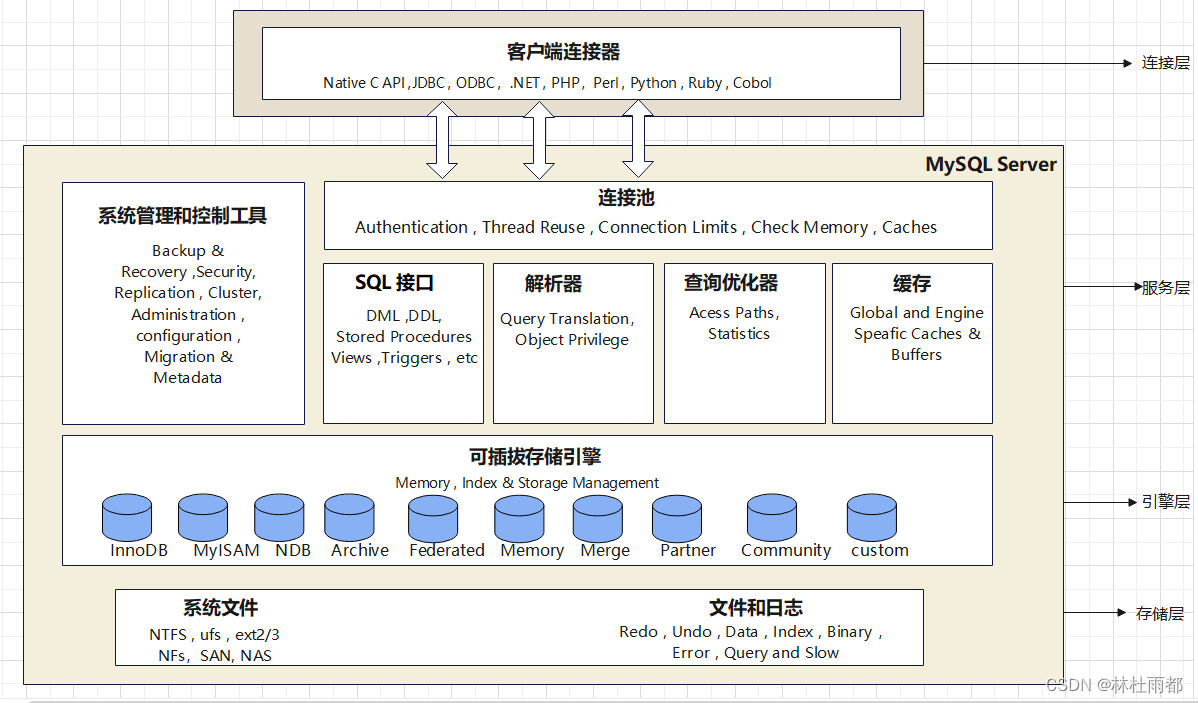
MySQL体系结构和四层架构介绍
MySQL体系结构图如下: 四层介绍 1. 连接层: 它的主要功能是处理客户端与MySQL服务器之间的连接(比如Java应用程序通过JDBC连接MySQL)。当客户端应用程序连接到MySQL服务器时,连接层对用户进行身份验证、建立安全连接并管理会话状态。它还处理…...

【产品运营】如何做好B端产品规划
产品规划是基于当下掌握的多维度信息,为追求特定目的,而制定的产品资源投入计划。 产品规划是基于当下掌握的多维度信息(客户需求、市场趋势、竞争对手、竞争策略等),为追求特定目的(商业增长、客户满意等&…...

ruoyi-启动
1 springboot 版本 git 地址 ruoyi-vue-pro: 🔥 官方推荐 🔥 RuoYi-Vue 全新 Pro 版本,优化重构所有功能。基于 Spring Boot MyBatis Plus Vue & Element 实现的后台管理系统 微信小程序,支持 RBAC 动态权限、数据权限…...
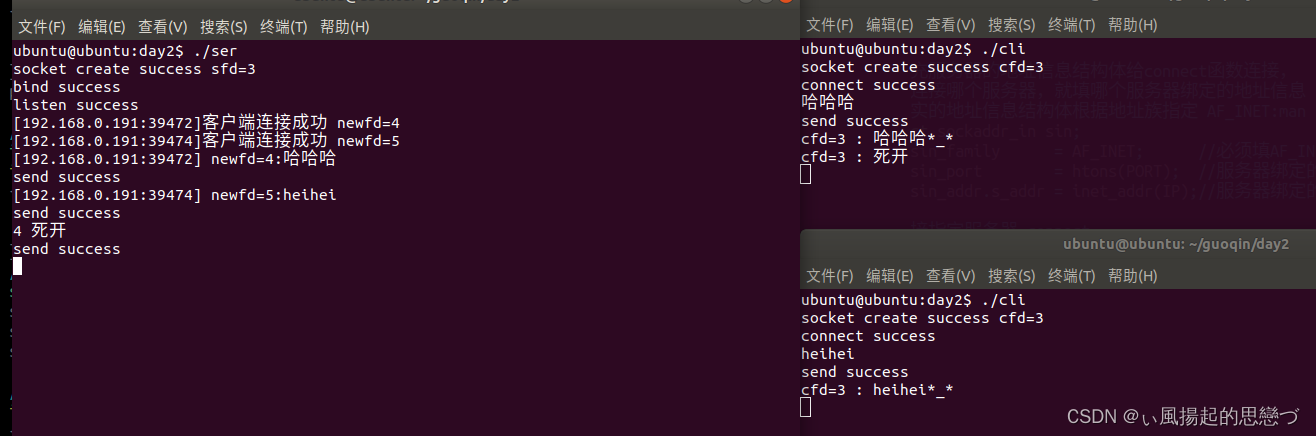
select完成服务器并发
服务器 #include <myhead.h>#define PORT 4399 //端口号 #define IP "192.168.0.191"//IP地址//键盘输入事件 int keybord_events(fd_set readfds); //客户端交互事件 int cliRcvSnd_events(int , struct sockaddr_in*, fd_set *, int *); //客户端连接事件 …...
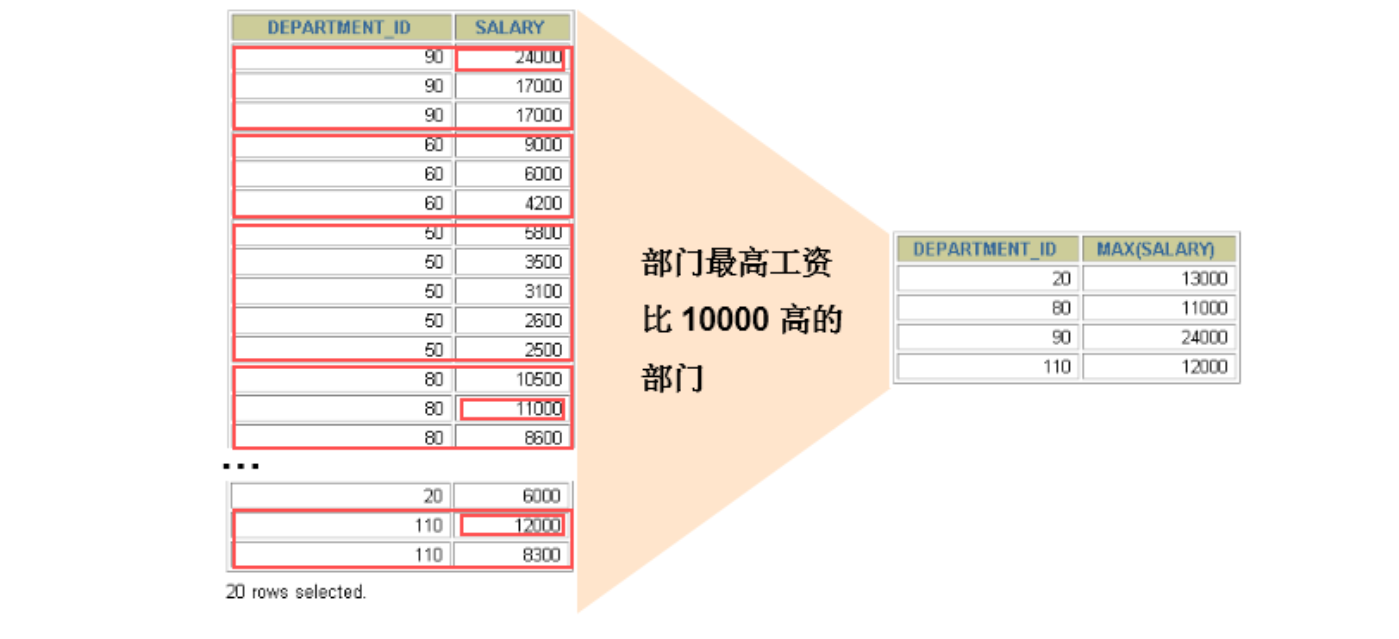
初级篇—第四章聚合函数
文章目录 聚合函数介绍聚合函数介绍COUNT函数AVG和SUM函数MIN和MAX函数 GROUP BY语法基本使用使用多个列分组WITH ROLLUP HAVING基本使用WHERE和HAVING的对比开发中的选择 SELECT的执行过程查询的结构SQL 的执行原理 练习流程函数 聚合函数介绍 聚合函数作用于一组数据&#x…...
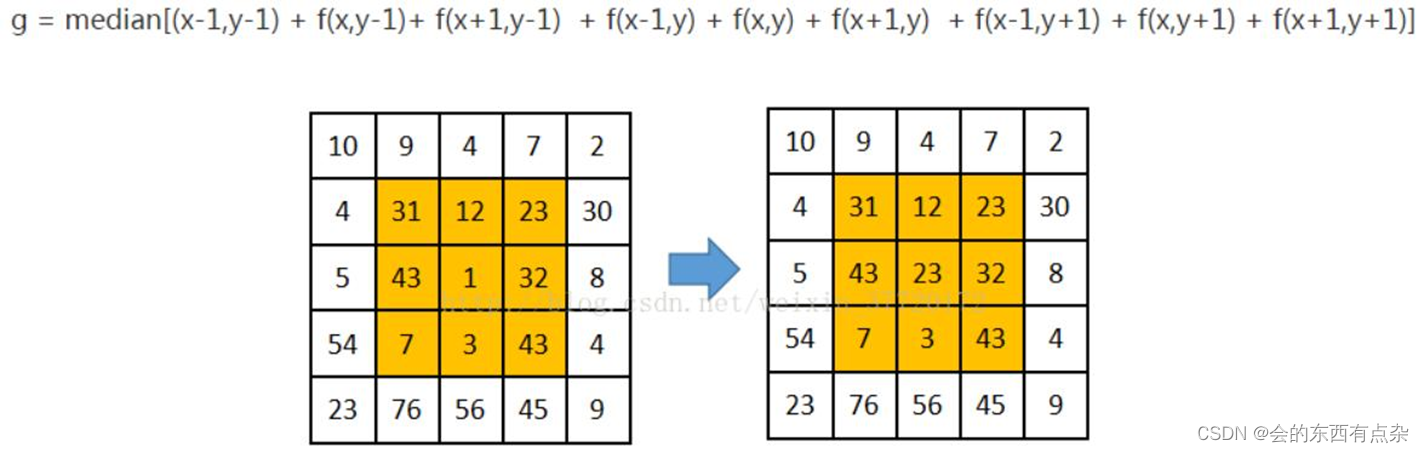
计算机图像处理-中值滤波
非线性滤波 非线性滤波是利用原始图像跟模版之间的一种逻辑关系得到结果,常用的非线性滤波方法有中值滤波和高斯双边滤波,分别对应cv2.medianBlur(src, ksize)方法和cv2.bilateralFilter(src, d, sigmaColor, sigmaSpace[, dst[, borderType]])方法。 …...

Golang中的包和模块设计
Go,也被称为Golang,是一种静态类型、编译型语言,因其简洁性和对并发编程的强大支持而受到开发者们的喜爱。Go编程的一个关键方面是其包和模块系统,它允许创建可重用、可维护和高效的代码。本博客文章将深入探讨在Go中设计包和模块…...
web:[极客大挑战 2019]Upload
题目 页面显示为一个上传,猜测上传一句话木马文件 先查看源代码看一下有没有有用的信息,说明要先上传图片,先尝试上传含有一句话木马的图片 构造payload <?php eval($_POST[123]);?> 上传后页面显示为,不能包含<&…...
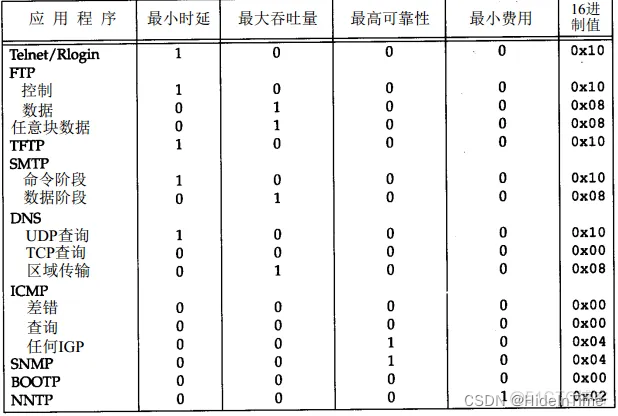
ICMP差错包
ICMP报文分类 Type Code 描述 查询/差错 0-Echo响应 0 Echo响应报文 查询 3-目的不可达 0 目标网络不可达报文 差错 1 目标主机不可达报文 差错 2 目标协议不可达报文 差错 3 目标端口不可达报文 差错 4 要求分段并设置DF flag标志报文 差错 5 源路由…...
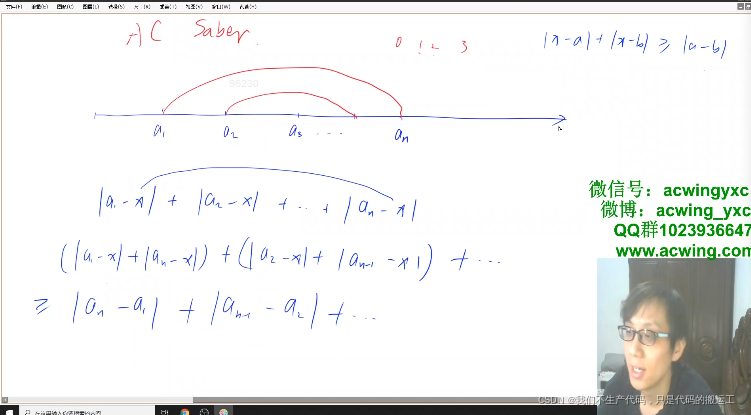
算法基础课第二部分
算法基础课 第四讲 数学知识AcWing1381. 阶乘(同余,因式分解) 质数AcWing 866. 质数的判定---试除法AcWing 868. 质数的判定---埃氏筛AcWing867. 分解质因数---试除法AcWing 197. 阶乘---分解质因数---埃式筛 约数AcWing 869. 求约数---试除法AcWing 870. 约数个数-…...

【数据结构】外部排序、多路平衡归并与败者树、置换-选择排序(生成初始归并段)、最佳归并树算法
目录 1、外部排序 1.1 基本概念 1.2 方法 2、多路平衡归并与败者树 2.1 K路平衡归并 2.2 败者树 3、置换-选择排序(生成初始归并段)编辑 4、最佳归并树 4.1 理论基础编辑 4.2 构造方法 编辑 5、各种排序算法的性质 1、外部排序 1.1 基本概…...

抽象工厂模式 创建性模式之五
在看这篇文章之前,请先看看“简单工厂模式”和“工厂方法模式”这两篇博文,会更有助于理解。我们现在已经知道,简单工厂模式就是用一个简单工厂去创建多个产品,工厂方法模式是每一个具体的工厂只生产一个具体的产品,然…...

servlet如何获取PUT和DELETE请求的参数
1. servlet为何不能获取PUT和DELETE请求的参数 Servlet的规范是POST的数据需要转给request.getParameter*()方法,没有规定PUT和DELETE请求也这么做 The Servlet spec requires form data to be available for HTTP POST but not for HTTP PUT or PATCH requests. T…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

Psychopy音频的使用
Psychopy音频的使用 本文主要解决以下问题: 指定音频引擎与设备;播放音频文件 本文所使用的环境: Python3.10 numpy2.2.6 psychopy2025.1.1 psychtoolbox3.0.19.14 一、音频配置 Psychopy文档链接为Sound - for audio playback — Psy…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...
