牛客网_HJ1_字符串最后一个单词的长度
HJ1_字符串最后一个单词的长度
- 原题
- 思路
- 代码
- 运行截图
- 收获
原题
字符串最后一个单词的长度
思路
从最后一个字符开始遍历,遇到第一个空格时的长度即为最后一个单词的长度
代码
#include <iostream>
#include <string>
using namespace std;int main() {string s;getline(cin, s);int len = s.length();for (int i = len - 1; i >= 0; i--) {if (s[i] == ' ') {cout << (len - 1 - i) << endl;return 0;} }cout << len << endl;return 0;
}
运行截图
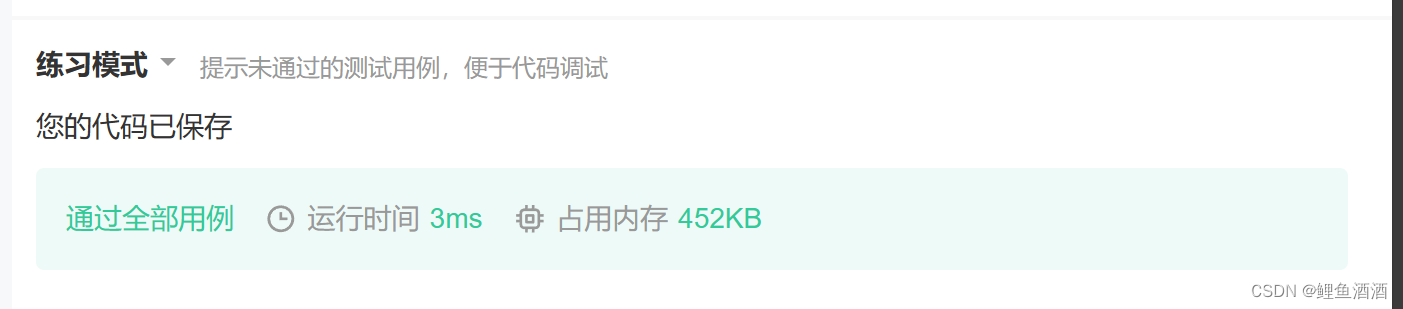
收获
- 用
cin >> s的形式,当遇到空格时会自动停止输入;而getline(cin, s)的形式,会把所有字符全部捕捉。
相关文章:

牛客网_HJ1_字符串最后一个单词的长度
HJ1_字符串最后一个单词的长度 原题思路代码运行截图收获 原题 字符串最后一个单词的长度 思路 从最后一个字符开始遍历,遇到第一个空格时的长度即为最后一个单词的长度 代码 #include <iostream> #include <string> using namespace std;int main…...

智算创新,美格智能助力智慧支付加速发展
9月21日,以“智算引领创新未来”为主题的紫光展锐2023泛物联网终端生态论坛在深圳举行。作为紫光展锐重要战略合作伙伴,美格智能标准模组产品线总经理郭强华、高级产品总监刘伟鹏受邀出席论坛。美格智能基于紫光展锐5G、4G、智能SoC、Cat.1 bis等芯片平台…...

常用SQL语法总结
1.库操作 1.1.创建数据库 CREATE DATABASE 语句用来创建一个新的数据库。 语法:CREATE DATABASE DatabaseName; DatabaseName 为数据库名字,它的名字必须是唯一的,不能和其它数据库重名。 1.2.删除数据库 DROP DATABASE语句用来删除已经…...

Promise击鼓传花的游戏
Promise击鼓传花的游戏 Promise系列导航前言一、学习Promise的原因二、揭开击鼓传花游戏的面纱补充小知识 Promise系列导航 1.Promise本质击鼓传花的游戏 2.Promise四式击鼓 3.Promise击鼓传花 4.Promise花落谁家知多少 前言 👨💻👨&…...

蓝桥杯每日一题2023.9.29
蓝桥杯大赛历届真题 - C&C 大学 B 组 - 蓝桥云课 (lanqiao.cn) 题目描述1 题目分析 看见有32位,我们以此为入手点, B代表字节1B 8b b代表位,32位即4个字节 (B) 1KB 1024B 1MB 1024KB (256 * 1024 * 1024) / 4 67108864 故答案…...
Spring Boot的自动装配中的@ConditionalOnBean条件装配注解在Spring启动过程中,是如何保证处理顺序靠后的
前言 为什么Spring Boot条件注解那么多,而标题中是ConditionalOnBean呢? 因为,相比之下我们用的比较多的条件装配注解也就是ConditionalOnClass、ConditionalOnBean了,而ConditionalOnClass对顺序并不敏感(说白了就是判…...
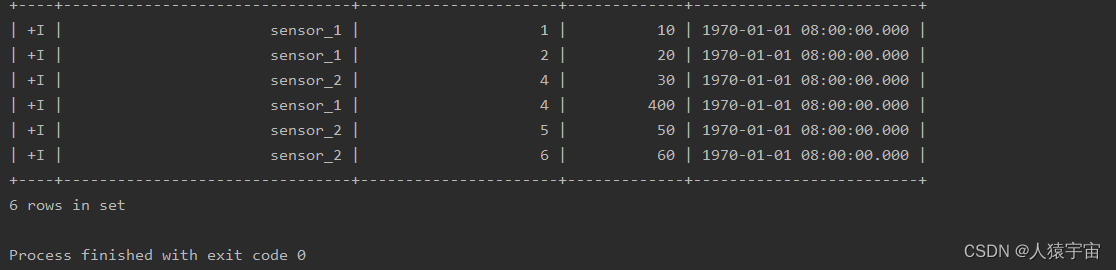
玩转数据-大数据-Flink SQL 中的时间属性
一、说明 时间属性是大数据中的一个重要方面,像窗口(在 Table API 和 SQL )这种基于时间的操作,需要有时间信息。我们可以通过时间属性来更加灵活高效地处理数据,下面我们通过处理时间和事件时间来探讨一下Flink SQL …...

【论文笔记】A Review of Motion Planning for Highway Autonomous Driving
文章目录 I. INTRODUCTIONII. CONSIDERATIONS FOR HIGHWAY MOTION PLANNINGA. TerminologyB. Motion Planning SchemeC. Specificities of Highway DrivingD. Constraints on Highway DrivingE. What Is at Stake in this Paper III. STATE OF THE ARTA. Taxonomy DescriptionB…...
YOLOv8改进算法之添加CA注意力机制
1. CA注意力机制 CA(Coordinate Attention)注意力机制是一种用于加强深度学习模型对输入数据的空间结构理解的注意力机制。CA 注意力机制的核心思想是引入坐标信息,以便模型可以更好地理解不同位置之间的关系。如下图: 1. 输入特…...
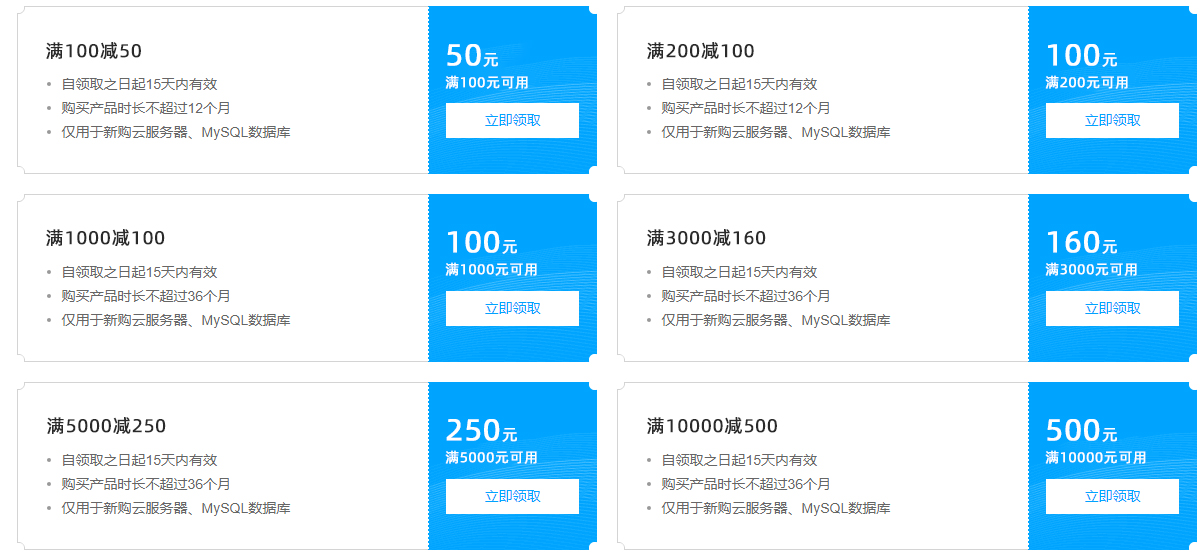
2023年10月腾讯云优惠活动汇总:腾讯云最新优惠、代金券整理
腾讯云作为国内领先的云服务提供商,致力于为用户提供优质、稳定的云服务。为了更好地满足用户需求,腾讯云推出了各种优惠活动。本文将给大家分享腾讯云最新优惠活动,帮助用户充分利用腾讯云提供的优惠。 一、腾讯云优惠券领取【点此领取】 腾…...
BUUCTF reverse wp 65 - 70
[SWPU2019]ReverseMe 反编译的伪码看不明白, 直接动调 这里显示"Please input your flag", 然后接受输入, 再和32进行比较, 应该是flag长度要求32位, 符合要求则跳转到loc_E528EE分支继续执行 动调之后伪码可以读了 int __cdecl main(int argc, const char **arg…...
xorm数据库操作之Join、Union
golang的数据库操作xorm使用起来非常方便,不用再自己写SQl语句,而且xorm自己给我们做了SQL防注入等操作,用起来既方便又安全。此次文章我不会记录xorm的基本操作,我值记录一些特殊用法问题,包括动态创建表单、基于xorm…...
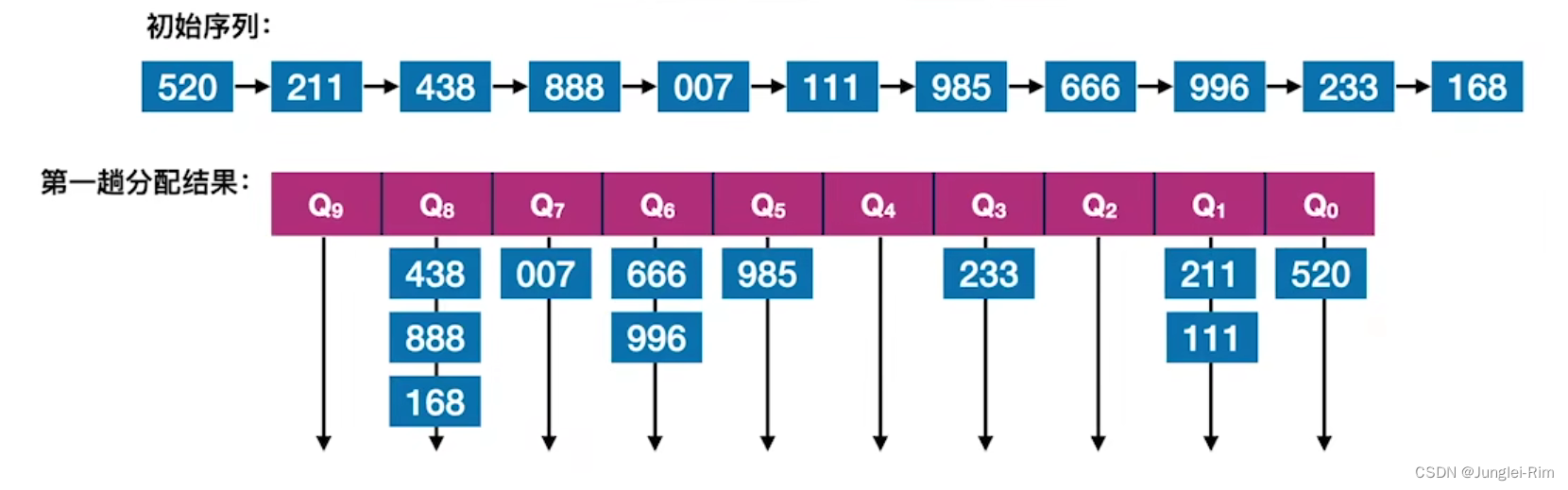
排序:基数排序算法分析
1.算法思想 假设长度为n的线性表中每个结点aj的关键字由d元组 ( k j d − 1 , k j d − 2 , k j d − 3 , . . . , k j 1 , k j 0 ) (k_{j}^{d-1},k_{j}^{d-2},k_{j}^{d-3},... ,k_{j}^{1} ,k_{j}^{0}) (kjd−1,kjd−2,kjd−3,...,kj1,kj0)组成, 其中&am…...
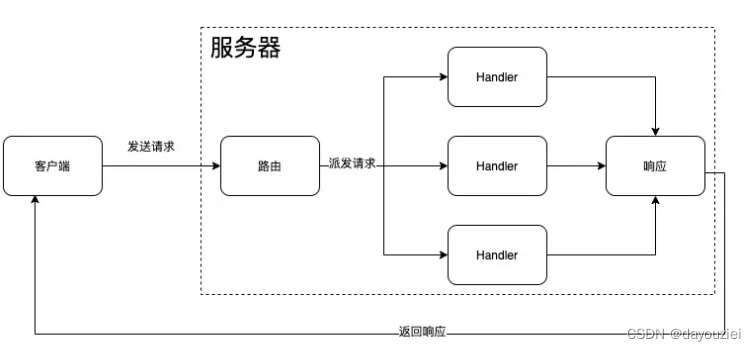
用go实现http服务端和请求端
一、概述 本文旨在学习记录下如何用go实现建立一个http服务器,同时构造一个专用格式的http客户端。 二、代码实现 2.1 构造http服务端 1、http服务处理流程 基于HTTP构建的服务标准模型包括两个端,客户端(Client)和服务端(Server)。HTTP 请求从客户端…...

幂级数和幂级数的和函数有什么关系?
幂级数和幂级数的和函数有什么关系? 本文例子引用自:80_1幂级数运算,逐项积分、求导【小元老师】高等数学,考研数学 求幂级数 ∑ n 1 ∞ 1 n x n \sum\limits_{n1}^{\infty}\frac{1}{n}x^n n1∑∞n1xn 的和函数 ÿ…...

Git多账号管理通过ssh 公钥的方式,git,gitlab,gitee
按照目前国内访问git,如果不科学上网,我们很大可能访问会超时。基于这个,所以我现在的git 配置已经增加到了3个了 一个公司gitlab,一个git,一个gitee. 以下基于这个环境,我们来说明下如何创建配置ssh公钥。…...

在nodejs常见的不良做法及其优化解决方案
在nodejs常见的不良做法及其优化解决方案 当涉及到在express和nodejs中开发应用程序时。遵循最佳实践对于确保项目的健壮性、可维护性和安全性至关重要。 在本文中,我们将探索开发人员经常遇到的几种常见的错误做法,并通过代码示例研究优化的最佳做法&…...

关于layui upload上传组件上传文件无反应的问题
最近使用layui upload组件时,碰到了上传文件无反应的问题,感到非常困惑。 因为使用layui upload组件不是一次两次了,之前每次都可以,这次使用同样的配方,同样的姿势,为什么就不行了呢? 照例先…...

容器网络之Flannel
第一个问题位置变化,往往是通过一个称为注册中心的地方统一管理的,这个是应用自己做的。当一个应用启动的时候,将自己所在环境的 IP 地址和端口,注册到注册中心指挥部,这样其他的应用请求它的时候,到指挥…...
:如何进行乳腺癌检测?)
SVM(下):如何进行乳腺癌检测?
⭐️⭐️⭐️⭐️⭐️欢迎来到我的博客⭐️⭐️⭐️⭐️⭐️ 🐴作者:秋无之地 🐴简介:CSDN爬虫、后端、大数据领域创作者。目前从事python爬虫、后端和大数据等相关工作,主要擅长领域有:爬虫、后端、大数据开发、数据分析等。 🐴欢迎小伙伴们点赞👍🏻、收藏⭐️、…...

Redis相关知识总结(缓存雪崩,缓存穿透,缓存击穿,Redis实现分布式锁,如何保持数据库和缓存一致)
文章目录 1.什么是Redis?2.为什么要使用redis作为mysql的缓存?3.什么是缓存雪崩、缓存穿透、缓存击穿?3.1缓存雪崩3.1.1 大量缓存同时过期3.1.2 Redis宕机 3.2 缓存击穿3.3 缓存穿透3.4 总结 4. 数据库和缓存如何保持一致性5. Redis实现分布式…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

Android15默认授权浮窗权限
我们经常有那种需求,客户需要定制的apk集成在ROM中,并且默认授予其【显示在其他应用的上层】权限,也就是我们常说的浮窗权限,那么我们就可以通过以下方法在wms、ams等系统服务的systemReady()方法中调用即可实现预置应用默认授权浮…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

深入理解Optional:处理空指针异常
1. 使用Optional处理可能为空的集合 在Java开发中,集合判空是一个常见但容易出错的场景。传统方式虽然可行,但存在一些潜在问题: // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...
)
华为OD最新机试真题-数组组成的最小数字-OD统一考试(B卷)
题目描述 给定一个整型数组,请从该数组中选择3个元素 组成最小数字并输出 (如果数组长度小于3,则选择数组中所有元素来组成最小数字)。 输入描述 行用半角逗号分割的字符串记录的整型数组,0<数组长度<= 100,0<整数的取值范围<= 10000。 输出描述 由3个元素组成…...

算术操作符与类型转换:从基础到精通
目录 前言:从基础到实践——探索运算符与类型转换的奥秘 算术操作符超级详解 算术操作符:、-、*、/、% 赋值操作符:和复合赋值 单⽬操作符:、--、、- 前言:从基础到实践——探索运算符与类型转换的奥秘 在先前的文…...
0609)
书籍“之“字形打印矩阵(8)0609
题目 给定一个矩阵matrix,按照"之"字形的方式打印这个矩阵,例如: 1 2 3 4 5 6 7 8 9 10 11 12 ”之“字形打印的结果为:1,…...
