【仔细理解】计算机视觉基础1——特征提取之Harris角点
Harris角点是图像特征提取中最基本的方法,本篇内容将详细分析Harris角点的定义、计算方法、特点。
一、Harris角点定义

在图像中,若以正方形的小像素窗口为基本单位,按照上图可以将它们划分三种类型如下:
- 平坦区域:在任何方向上移动窗口,窗口内容变化都不大
- 边缘:在某一方向上移动窗口,窗口内容变化较大(如图中上下移动基本不变,而左右移动时窗口内容变化较大)
- 角点:在任何方向上移动窗口,窗口内容变化都很大
从人类角度直观理解,图像的关键特征点应该是那些与周围图像存在明显差异的点。
(以灰度图为例,其实就是该点的灰度值与周围点差别较大,那么就可以通过计算其与周围点的灰度差值,即导数来判断)。
以像素窗口为基本单位时,我们将这些与周围图像差异较大的小窗口称为角点,用它们就可以代表图像中具有辨别性的、关键特征区域。
二、Harris角点计算方法
1. 计算窗口内容差异情况
角点是指与周围存在较大内容差异的像素窗口,那么我们首先要给出小窗口与周围窗口的差异情况的计算方法,在方向(u,v)上移动称之为窗口响应值E(u,v)

E(u,v)=∑x,yw(x,y)[I(x+u,y+v)−I(x,y)]2E(u,v)=\sum_{x,y}w(x,y)[I(x+u,y+v)-I(x,y)]^2E(u,v)=x,y∑w(x,y)[I(x+u,y+v)−I(x,y)]2
- 红色小窗口为原始窗口用I(x,y)表示,绿色为移动后的窗口I(x+u,y+v),其中(u,v)其实便代表了移动的方向。
- w(x,y)代表了原始窗口中不同像素点的权重
- 公式含义即为将移动前后每个像素的灰度值差求平方,并根据各像素点权重求和作为两个窗口的内容差异E(u,v)
2.窗口内容差异E =》由矩阵M决定
为了更方便的计算窗口在移动前后的响应值,我们将E(u,v)的公式进行一系列的数学变换,首先是做二元泰勒展开:

展开式前两项为0,最后一项可以通过矩阵的形式表示为:
E(u,v)≈[uv]M[uv]E(u,v) ≈ \begin{bmatrix} u&v\end{bmatrix} M \begin{bmatrix} u \\ v \end{bmatrix}E(u,v)≈[uv]M[uv]
M=∑x,yw(x,y)[Ix2IxIyIxIyIy2]M=\sum_{x,y}w(x,y)\begin{bmatrix}I_{x}^2&I_xI_y\\ I_xI_y&I_{y}^2\end{bmatrix}M=x,y∑w(x,y)[Ix2IxIyIxIyIy2]
根据公式我们发现,E(u,v)的取值即窗口在不同方向(u,v)移动后的相对差异情况关键取决于矩阵M,即不用关心方向(u,v),而是通过矩阵M就可以判断是否为角点(IxI_xIx代表在x方向上的梯度)
3.窗口内容差异E =》由矩阵M决定 =》由特征值λ决定
通过矩阵M判断角点可以进一步简化为通过矩阵M的特征值λ来判断。
当M可以变化为对角矩阵时(不能对角化的情况稍后说明),E(u,v)最终结果为u2λ1+v2λ2u^{2}λ_{1}+v^{2}λ_{2}u2λ1+v2λ2,假设取值为常数c(取1),即有:

E(u,v)=[uv][λ100λ2][uv]=u2λ1+v2λ2E(u,v)=\begin{bmatrix} u&v\end{bmatrix} \begin{bmatrix}λ_{1}&0\\0&λ_{2}\end{bmatrix} \begin{bmatrix} u \\ v \end{bmatrix}=u^{2}λ_{1}+v^{2}λ_{2}E(u,v)=[uv][λ100λ2][uv]=u2λ1+v2λ2
u2λ1+v2λ2=1\frac{u^2}{λ_{1}}+\frac{v^2}{λ_{2}}=1λ1u2+λ2v2=1
该方程的几何表示为椭圆如下:

- 即当在以长短轴为方向的坐标系上,椭圆边界线上为移动后具有相同响应值E(u,v)的点;
- 即当要让窗口移动后具有相同响应值(内容差异),沿短轴方向移动最短距离,沿长轴移动需要的距离最长——代表短轴是梯度变化最快的方向,长轴是梯度变化最慢方向
若二阶矩矩阵M不能直接对角化时,我们可以将其转为以下形式:
M=R−1[λ100λ2]RM=R^{-1} \begin{bmatrix}λ_1&0\\0&λ_2 \end{bmatrix}RM=R−1[λ100λ2]R
其中R为旋转矩阵,即此时几何表示为发生了旋转的椭圆,而长短轴依然代表梯度变化最慢和最快的方向:

因此,根据角点的定义可知——任何方向上都有较大梯度变化 =》椭圆的长短轴都要短 =》特征值λ1λ_{1}λ1、λ2λ_{2}λ2都要大

- 当λ1λ_{1}λ1、λ2λ_{2}λ2都大,在任何方向梯度都大、E增加的快,即为角点
- 当λ1λ_{1}λ1、λ2λ_{2}λ2其中一个远比另一个大,则说明在最快方向变化特快、同时有一个方向几乎不变,这是边缘区域
- 当λ1λ_{1}λ1、λ2λ_{2}λ2都很小,在任何方向梯度逗笑、E变化的慢,即为平坦区域
4.窗口内容差异E =》由矩阵M决定 =》由特征值λ决定 =》由计算R决定
R由特征值λ1λ_{1}λ1、λ2λ_{2}λ2计算得到,公式为:
R=Det(M)−α∗Trace(M)2=λ1λ2−α(λ1+λ2)2R=Det(M)-α*Trace(M)^2=λ_{1}λ_{2}-α(λ_{1}+λ_{2})^2R=Det(M)−α∗Trace(M)2=λ1λ2−α(λ1+λ2)2
可知当λ1λ_{1}λ1、λ2λ_{2}λ2分别处于3中所说的三种状态时,对应R有:

- 当λ1λ_{1}λ1、λ2λ_{2}λ2都大,R>0,即为角点
- 当λ1λ_{1}λ1、λ2λ_{2}λ2其中一个远比另一个大,R<0,这是边缘区域
- 当λ1λ_{1}λ1、λ2λ_{2}λ2都很小,R接近0,即为平坦区域
三、Harris角点的特点

上图为使用Harris角点检测获取的关键点。
对于理想的图像特征点,应该可以抵抗光照、旋转、平移、尺度等变化,即具有不变性(Invariance)或协变性(Covariance)
- 不变性(Invariance):变换后原特征点仍能被检测出来、且位置不变;
- 协变性(Covariance):变换后原特征点仍能被检测出来,但位置可能发生变化
3.1 优点
针对Harris角点来说,能够抵抗光照、旋转、平移变换(该部分图片来自知乎@饭饭):

光照:光照变换会使得区域像素灰度值整体提高或降低
- 当增量或这减量相同(灰度平移)时,对基于像素间灰度差值(梯度)的角点判断方法不影响,已经被检测出来的角点能够保持不变性。
- 当相比原来灰度成倍增加或减少(尺度平移),阈值不变时可能导致检测角点的数量增加或减少,但同时被检测出的相同角点位置不变

旋转:当发生旋转时,相当于二阶矩矩阵对应几何椭圆旋转(即梯度变化最快最慢的方向发生变化),但特征值不变,角点本身只有位置可能发生了变化,即具有协变性
平移:与旋转类似,角点位置发生变化,具有协变性,但梯度变化最快最慢方向不变
3.2 缺点
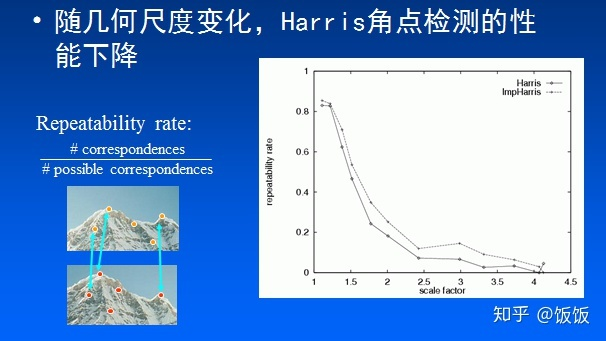
Harris角点并不具有尺度不变性,当图像尺度缩小时,原来的角点区域可能被判断为边缘、甚至进一步平坦区域;反之尺度放大时也会导致原角点找不到对应角点的情况出现;为了在此基础上保持尺度不变性,可以使用后续的SIFT特征检测方法。
相关文章:

【仔细理解】计算机视觉基础1——特征提取之Harris角点
Harris角点是图像特征提取中最基本的方法,本篇内容将详细分析Harris角点的定义、计算方法、特点。 一、Harris角点定义 在图像中,若以正方形的小像素窗口为基本单位,按照上图可以将它们划分三种类型如下: 平坦区域:在任…...
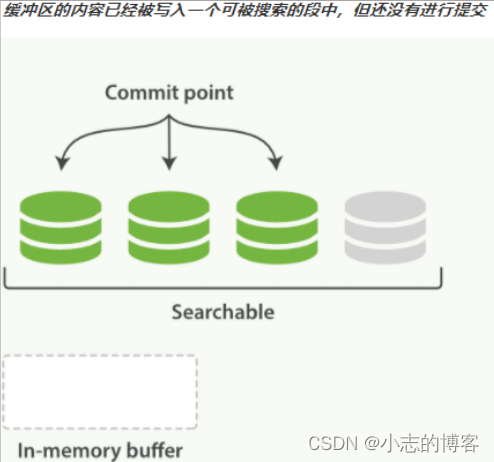
Elasticsearch7.8.0版本进阶——近实时搜索
目录一、近实时搜索的概述1.1、按段(per-segment)搜索1.2、更轻量的方式搜索二、为什么Elasticsearch是 近 实时搜索三、如何解决索引了一个文档然后却没有搜到四、哪种情况不需要每秒刷新4.1、使用 Elasticsearch 索引大量的日志文件4.2、使用 Elastics…...
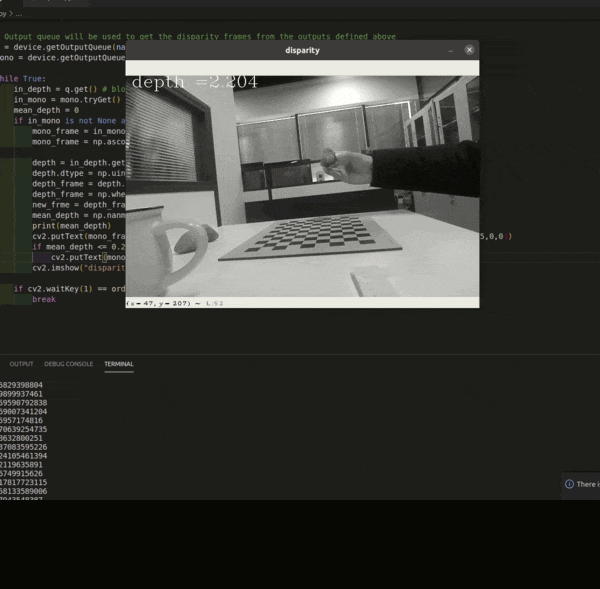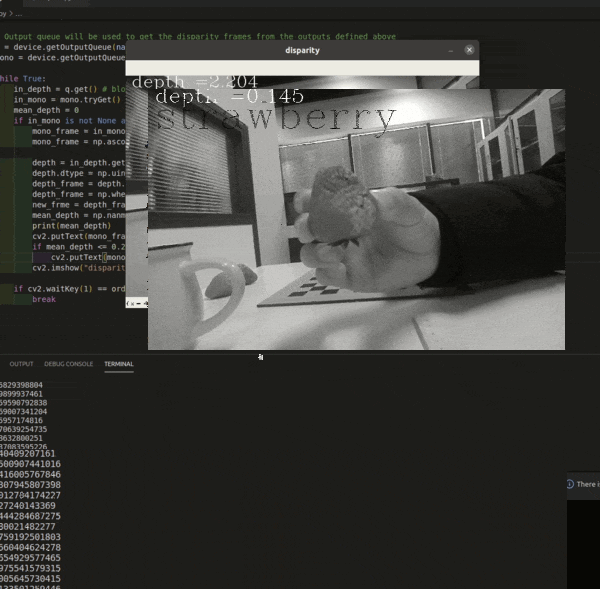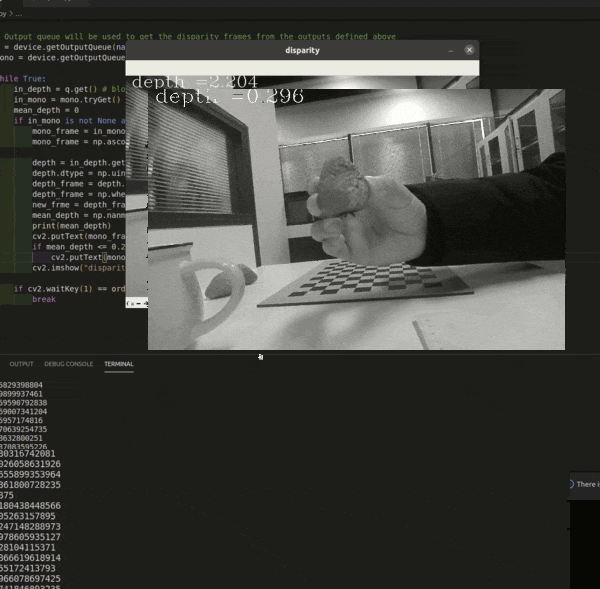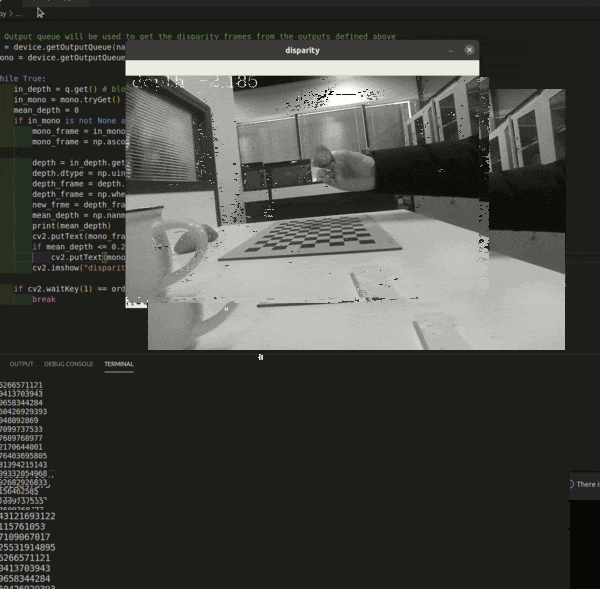
OAK相机深度流探测草莓距离
编辑:OAK中国 首发:oakchina.cn 喜欢的话,请多多👍⭐️✍ 内容可能会不定期更新,官网内容都是最新的,请查看首发地址链接。 ▌前言 Hello,大家好,这里是OAK中国,我是助手…...
的相关知识及指令)
文件共享服务器(CIFS)的相关知识及指令
文件共享服务器(CIFS) 微软开发的 共享服务器概述 通过网络提供文件共享拂去,提供文件下载和上传服务(类似于FTP服务器) 创建共享 通过本地登录时,仅受NTFS权限的控制通过网络访问时,受共享…...

springcloud-2service consumer
创建使用会员微服务模块-service consumer思路分析/图解创建Moduel(member-service-consumer-80) & 完成配置new Module->member-service-consumer-80->finish检查父子项目的pom是否添加相应的对应module和parent本项目的pom.xml可以参考provider的,并删掉…...
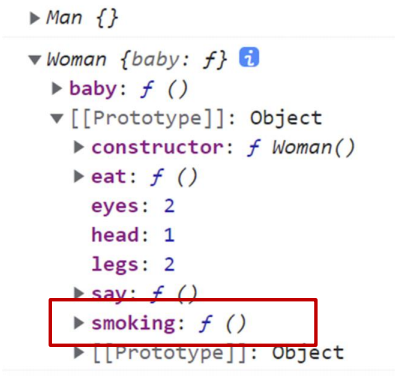
JavaScript 进阶--charater3
文章目录前言一、编程思想1.1 面向过程介绍1.2 面向对象编程 (oop)对比二、构造函数三、原型3.1原型3.2 constructor 属性3.3 对象原型3.4 原型继承3.5 原型链总结前言 🆑学习目标 理解面向对象思想,掌握函数原型对象运用面向对象封装继承特点…...

Solon2 之基础:三、启动参数说明
启动参数,在应用启动后会被静态化(为了内部更高效的利用)。比如,想通过体外扩展加载配置,是不能改掉它们的。 1、启动参数 启动参数对应的应用配置描述–envsolon.env环境(可用于内部配置切换)…...

引入防关联浏览器以防止数据盗窃
目前,互联网已成为我们生活中不可缺少的且不断发展的一部分。因此,互联网变得更加复杂和多样化,每天都有新的技术、服务和应用推出。在这个不断变化的环境中,虚拟浏览器最近作为一种革命性的新方式出现在互联网上。 简而言之&…...
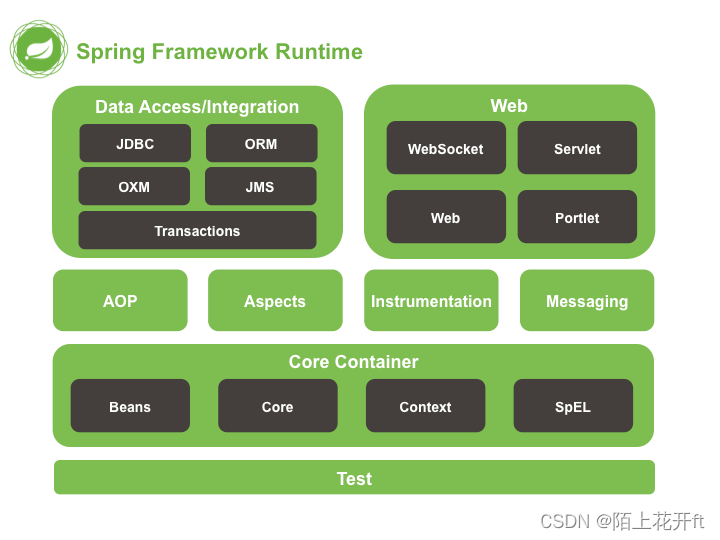
Spring的一些知识点
什么是Spring? Spring是一种轻量级的开发框架,旨在提高开发人员的开发效率以及系统的可维护性。 Spring的核心模块 Spring Core是基础模块,可以说Spring的其他功能都要依赖于该类库,主要提供IOC的依赖注入功能; Spri…...
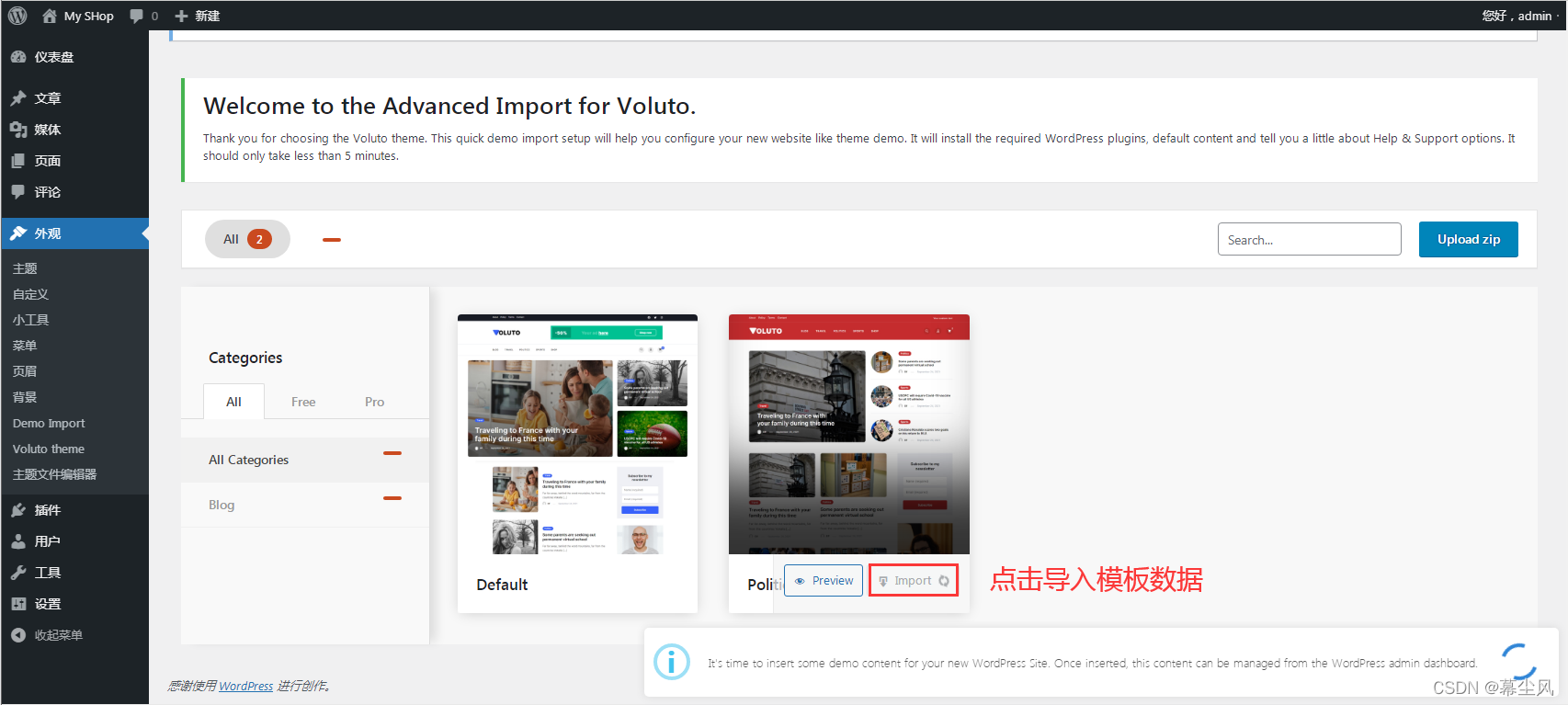
使用WordPress快速搭建外贸网站教程
一、下载安装 1、首先前往官方下载wordPress框架,下载地址:Download | WordPress.org 2、把下载好的安装包上传到我们的服务器,解压 3、我使用的搭建环境是宝塔Linux CentOS 7.9(Apache2.4mysql5.6php7.4)…...

在 vue 或 react 项目中使用 mockjs 搭建 mock server
有时候,在公司里一些项目开发前,后端接口没那么快给到前端时,前端可以先跟后端约定好各个接口的请求路径、请求参数以及返回数据格式,先整理出一份接口文档,这样前端可以通过mockjs参考接口文档,自己先模拟…...

【十一届蓝桥杯】
ans 0for i in range(1,2021):ans (str(i).count(2))print(ans)第二个def check(s):return s 2020matrix []s input()while 1 not in s:matrix.append(list(s))s input()n,m len(matrix),len(matrix[0])ans 0for i in range(n):for j in range(m):if i 3 < n and c…...
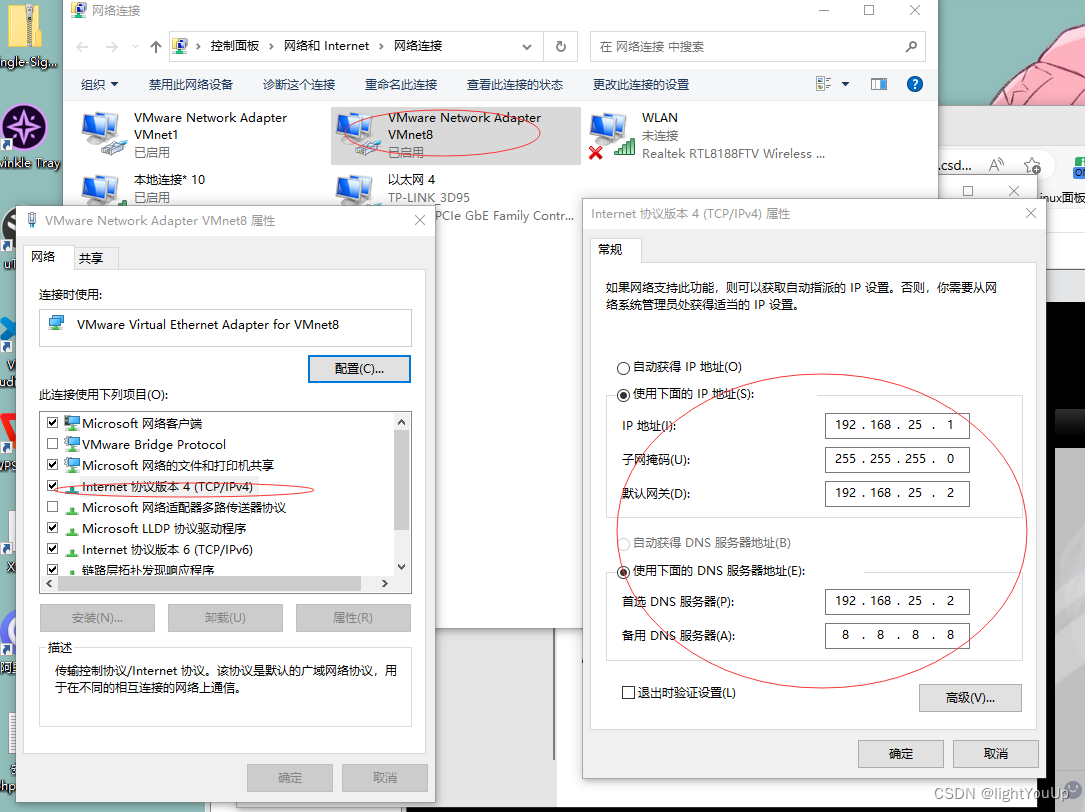
vm 网络配置
点击NAT设置,配置本台虚拟机ip(注意网关要在同一个网段),配置对应端口 然后添加映射端口: 然后选择网络适配器 选择vm8网卡 配置网卡静态ip #查看网卡 ip addr #修改网卡配置 cd /etc/sysconfig/network-scripts…...
)
2023年CDGA考试-第11章-数据仓库和商务智能(含答案)
2023年CDGA考试-第11章-数据仓库和商务智能(含答案) 单选题 1.商务智能是在构建好数据仓库以后,支撑业务决策 风险管理等更高层面的分析,以下描述不符合的是: A.提供数据查询、分析和报表等珈能 B.通过收集。整合 分析和探索数据来支持决策 C.对数据进行可视化 D.从数据中…...

从0-1搭建流媒体系统之live555 安装、运行、转发、拉流
流媒体开发系列文章 文章目录 流媒体开发系列文章前言一、环境准备?二、安装编译过程三、vscode调试代码四、代码分析总结前言 目前、比较有名的流媒体服务器有ZLMediaKit、srs、live555、eadydarwin等。因为srs是单线程服务、对于多核服务器的支持需要通过部署多个服务来充分…...
搭建个人博客保姆级教程(二)
文章目录一. Springboot项目打包成jar包二. mySql部署三. UI 项目部署一. Springboot项目打包成jar包 使用IDEA进行打包,当然也有其他部署方式,如使用maven进行打包,可自行查询资料。 1.打开项目,右击项目选中Open Module Settin…...

数字图像处理与Python实现-Pillow图像处理
Pillow图像处理 文章目录 Pillow图像处理1、Pillow介绍2、 Pillow 中的Image模块和Image类2.1 读取图像2.2 图像大小调整2.3 图像保存2.4 图像旋转2.5 图像储存模式与转换3、图像滤波处理3.1 使用卷积核进行滤波3.2 图像模糊、锐化和平滑3.3 边缘检测、边缘增强和浮雕效果3.4 图…...

HMM隐马尔可夫模型 | 关键原理+面试知识点
😄 HMM之前跟人生导师:李航学习过,这里结合自己的理解,精简一波HMM,总结一下面试中高频出现的要点。 文章目录 1、何为HMM?2、HMM三要素:3、HMM两大强假设4、HMM三个基本问题 :5、HMM中涉及的算法6、HMM缺点7、面试高频题7.1、HMM中为何引入维特比算法作为预测算法?…...

【Leedcode】数据结构中链表必备的面试题(第三期)
【Leedcode】数据结构中链表必备的面试题(第三期) 文章目录【Leedcode】数据结构中链表必备的面试题(第三期)一、第一题1.题目2.思路3.源代码二、第二题1.题目2.思路(1)第一种情况:偶数个链表(2)第二种情况:…...
【数学,二分,暴力,思维】)
D1.Chopping Carrots (Easy Version)【数学,二分,暴力,思维】
链接 理论基础 已知正整数a,v,求证m⌊av⌋是满足⌊am⌋⩾v的最大的m,其中x是正整数已知正整数a,v,求证m\lfloor \frac {a}{v} \rfloor是满足\lfloor \frac {a}{m} \rfloor \geqslant v的最大的m,其中x是正整数已知正整数a,v,求证m⌊va⌋是满足⌊ma⌋…...

19c补丁后oracle属主变化,导致不能识别磁盘组
补丁后服务器重启,数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后,存在与用户组权限相关的问题。具体表现为,Oracle 实例的运行用户(oracle)和集…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...
