[Machine learning][Part3] numpy 矢量矩阵操作的基础知识
很久不接触数学了,machine learning需要用到一些数学知识,这里在重温一下相关的数学基础知识
矢量
矢量是有序的数字数组。在表示法中,矢量用小写粗体字母表示。矢量的元素都是相同的类型。例如,矢量不包含字符和数字。数组中元素的数量通常被称为维度,数组中元素的数量通常被称为维度,可以使用索引引用矢量的元素。在数学设置中,索引通常从 1 到 n。在计算机科学和这些实验室中,索引通常从 0 运行到 n-1。下面是两个的对比,在计算机中我们使用的是左边code的那种方式,也就是0到n-1

Numpy中的阵列
NumPy 的基本数据结构是一个可索引的 n 维数组,其中包含相同类型 (dtype) 的元素。
一维向量的操作:
向量创建
创建一个指定shape的一维向量,参数可以是整数、元祖等等,参数表示要创建的序列的shape
a= np.zeros(4); print(f"np.zeros(4) : a = {a}, a shape = {a.shape}, a data type = {a.dtype}")
a= np.zeros((4,)); print(f"np.zeros(4,) : a = {a}, a shape = {a.shape}, a data type = {a.dtype}")
a= np.random.random_sample(4); print(f"np.random.random_sample(4): a = {a}, a shape = {a.shape}, a data type = {a.dtype}")创建一个不指定shape的一维向量
a = np.arange(4.); print(f"np.arange(4.): a = {a}, a shape = {a.shape}, a data type = {a.dtype}")
a = np.random.rand(4); print(f"np.random.rand(4): a = {a}, a shape = {a.shape}, a data type = {a.dtype}")创建指定值的一维向量
a = np.array([5, 4, 3, 2]); print(f"np.array([5,4,3,2]): a = {a}, a shape = {a.shape}, a data type = {a.dtype}")
a = np.array([5., 4, 3, 2]); print(f"np.array([5.,4,3,2]): a = {a}, a shape = {a.shape}, a data type = {a.dtype}")向量操作
获取向量元素:通过index和切片可以获得,这个和列表的操作相似。
-
通过index获得:
a = np.arange(10)
print(a)
# 获取Index = 2的元素
print(f"a[2].shape: {a[2].shape} a[2] = {a[2]}, Accessing an element returns a scalar")# 获取最后一个元素
print(f"a[-1]={a[-1]}")# index 必须在向量有效范围以内,否则会报错
try:c = a[10]
except Exception as e:print(e)- 切片获取元素
# 切片操作通过(start:stop:step)这个三个参数来控制要获取的元素,
# 切片操作是左闭右开,也就是包括index=start的值,但是不包括index=stop的值
# 向量切片操作
a = np.arange(10)
print(f"a = {a}")#获取向量中的从index=2开始到Index=7结束的5个元素, 第三个参数1表示step=1,代表连续取值 (start:stop:step)
c = a[2:7:1]; print("a[2:7:1] = ", c)# 获取向量中的从index=2开始到Index=7结束的元素, 第三个参数1表示step=2,代表隔一个index取一个值 (start:stop:step)
c = a[2:7:2]; print("a[2:7:2] = ", c)# 取index 大于3的所有值
c = a[3:]; print("a[3:] = ", c)# 取index小于3的所有值
c = a[:3]; print("a[:3] = ", c)# 取所有的值
c = a[:]; print("a[:] = ", c)- 单个向量的操作
a = np.array([1, 2, 3, 4])
print(f"a: {a}")
# 将向量中的元素全部变为相反数
b = -a
print(f"b: {b}")
# 计算向量中所有元素的和并返回一个和的标量
b = np.sum(a)
print(f"b = np.sum(a) : {b}")
# 求向量的平均值
b = np.mean(a)
print(f"b = np.mean(a): {b}")
# 对向量中每个元素求平法
b = a**2
print(f"b = a**2 : {b}")- 对向量元素的操作,numpy很多对数字的操作也都是用于向量的
# 向量a+向量b, 两个向量长度必须相同,不然会报error
a = np.array([1, 2, 3, 4])
b= np.array([-1, -2, 3, 4])print(f"Binary operators work element wise: {a + b}")# 标量和向量的操作a = np.array([1, 2, 3, 4])
b = 5 * a
print(f"b = 5 * a : {b}")- 向量与向量的点积

自定义一个实现点积的方法:
def my_dot(a,b):"""Compute the dot product of two vectorsArgs:a (ndarray (n,)): input vectorb (ndarray (n,)): input vector with same dimension as aReturns:x (scalar):"""x = 0for i in range(a.shape[0]):x= x+a[i]*b[i]return x# test my_dot()a = np.array([1,2,3,4])
b = np.array([-1, 4, 3, 2])print(f"my_dot(a, b) = {my_dot(a, b)}")使用Numpy中的点积方法:
# 使用numpy中的dot来计算点积,返回一个标量
a = np.array([1, 2, 3, 4])
b = np.array([-1, 4, 3, 2])
c = np.dot(a, b)
print(f"NumPy 1-D np.dot(a, b) = {c}, np.dot(a, b).shape = {c.shape} ")
c = np.dot(b, a)
print(f"NumPy 1-D np.dot(b, a) = {c}, np.dot(a, b).shape = {c.shape} ")然后对上面两种计算点积的方法做个效率上的对比
# 对比一下numpy 的dot和自己写的my_dot的效率如何,可以看出numpy中的效率要高很多
np.random.seed(1)
a = np.random.rand(10000000) # very large arrays
b = np.random.rand(10000000)tic = time.time() # capture start time
c = np.dot(a, b)
toc = time.time() # capture end timeprint(f"np.dot(a, b) = {c:.4f}")
print(f"Vectorized version duration: {1000*(toc-tic):.4f} ms ")tic = time.time() # capture start time
c = my_dot(a,b)
toc = time.time() # capture end timeprint(f"my_dot(a, b) = {c:.4f}")
print(f"loop version duration: {1000*(toc-tic):.4f} ms ")del(a);del(b) #remove these big arrays from memory运行结果为:可以看到numpy的耗时要少很多
my_dot(a, b) = 24
NumPy 1-D np.dot(a, b) = 24, np.dot(a, b).shape = ()
NumPy 1-D np.dot(b, a) = 24, np.dot(a, b).shape = ()
np.dot(a, b) = 2501072.5817
Vectorized version duration: 6.5184 ms
my_dot(a, b) = 2501072.5817
loop version duration: 2430.3420 ms 矩阵
矩阵是一个二维阵列,里面的元素都是同一类型的。一般用大写黑体字母表示。用两个下标m,n表示,m表示行数,n表示列数。通过两个下标可以访问指定的元素
矩阵操作
创建矩阵
与创建向量的方法一样,只是这里的参数要换成元祖
a = np.zeros((1, 5))
print(f"a shape = {a.shape}, a = {a}")a = np.zeros((2, 1))
print(f"a shape = {a.shape}, a = {a}")a = np.random.random_sample((1, 1))
print(f"a shape = {a.shape}, a = {a}")# 2.创建指定元素的矩阵
a= np.array([[5],[4],[3]])
print(f" a shape = {a.shape}, np.array: a = {a}")
矩阵的操作
# 3.矩阵的操作
# 3.1 下标访问
# reshape 是一种比较方便的方法创建矩阵,
a = np.arange(6).reshape(-1, 2) #reshape(-1,2) 表示生成一个6/2行,2列的矩阵,也就是3行两列的矩阵
print(f"a.shape:{a.shape},\na={a}")
# 访问一个元素
print(f"\na[2.0].shape:{a[2:0].shape},a[2,0]={a[2:0]}, type(a[2,0])={type(a[2,0])} Accessing an element returns a scalar\n")
# 访问一行
print(f"a[2].shape:{a[2].shape},a[2] = {a[2]},type(a[2]) = {type(a[2])}")# 3.2切片访问
a = np.arange(20).reshape(-1, 10)
print(f"a=\n{a}")# 访问一行中5个连续的元素(start:stop:step)
print("a[0,2:7:1]=",a[0, 2:7:1], "a[0,2:7:1].shape=", a[0, 2:7:1].shape, "a-1D array")# 访问两行中5个连续的元素(start:stop:step)
print("a[:, 2:7:1] = \n", a[:, 2:7:1], ", a[:, 2:7:1].shape =", a[:, 2:7:1].shape, "a 2-D array")# 访问矩阵所有元素
print("a[:,:] = \n", a[:,:], ", a[:,:].shape =", a[:,:].shape)# 访问一行中的所有元素,方法1
print("a[1,:] = ", a[1,:], ", a[1,:].shape =", a[1,:].shape, "a 1-D array")
# 访问一行中的所有元素,方法2
print("a[1] = ", a[1], ", a[1].shape =", a[1].shape, "a 1-D array")相关文章:

[Machine learning][Part3] numpy 矢量矩阵操作的基础知识
很久不接触数学了,machine learning需要用到一些数学知识,这里在重温一下相关的数学基础知识 矢量 矢量是有序的数字数组。在表示法中,矢量用小写粗体字母表示。矢量的元素都是相同的类型。例如,矢量不包含字符和数字。数组中元…...

【中秋国庆不断更】HarmonyOS对通知类消息的管理与发布通知(上)
一、通知概述 通知简介 应用可以通过通知接口发送通知消息,终端用户可以通过通知栏查看通知内容,也可以点击通知来打开应用。 通知常见的使用场景: 显示接收到的短消息、即时消息等。显示应用的推送消息,如广告、版本更新等。显示…...

喜讯 | 怿星科技获评SAE“优秀核心零部件企业”,测试软件平台工具广受赞誉
2023年9月22日-23日,SAE 2023汽车智能与网联技术国际学术会议成功举行。此次学术会议由SAE International与南昌智能新能源汽车研究院联合主办,大会汇聚了来自国内外智能网联领域的顶尖专家和学者。大会同期颁布的奖项旨在向行业推选出更多新时代涌现的杰…...

基于Java的医院预约挂号系统设计与实现(源码+lw+部署文档+讲解等)
文章目录 前言具体实现截图论文参考详细视频演示为什么选择我自己的网站自己的小程序(小蔡coding)有保障的售后福利 代码参考源码获取 前言 💗博主介绍:✌全网粉丝10W,CSDN特邀作者、博客专家、CSDN新星计划导师、全栈领域优质创作…...
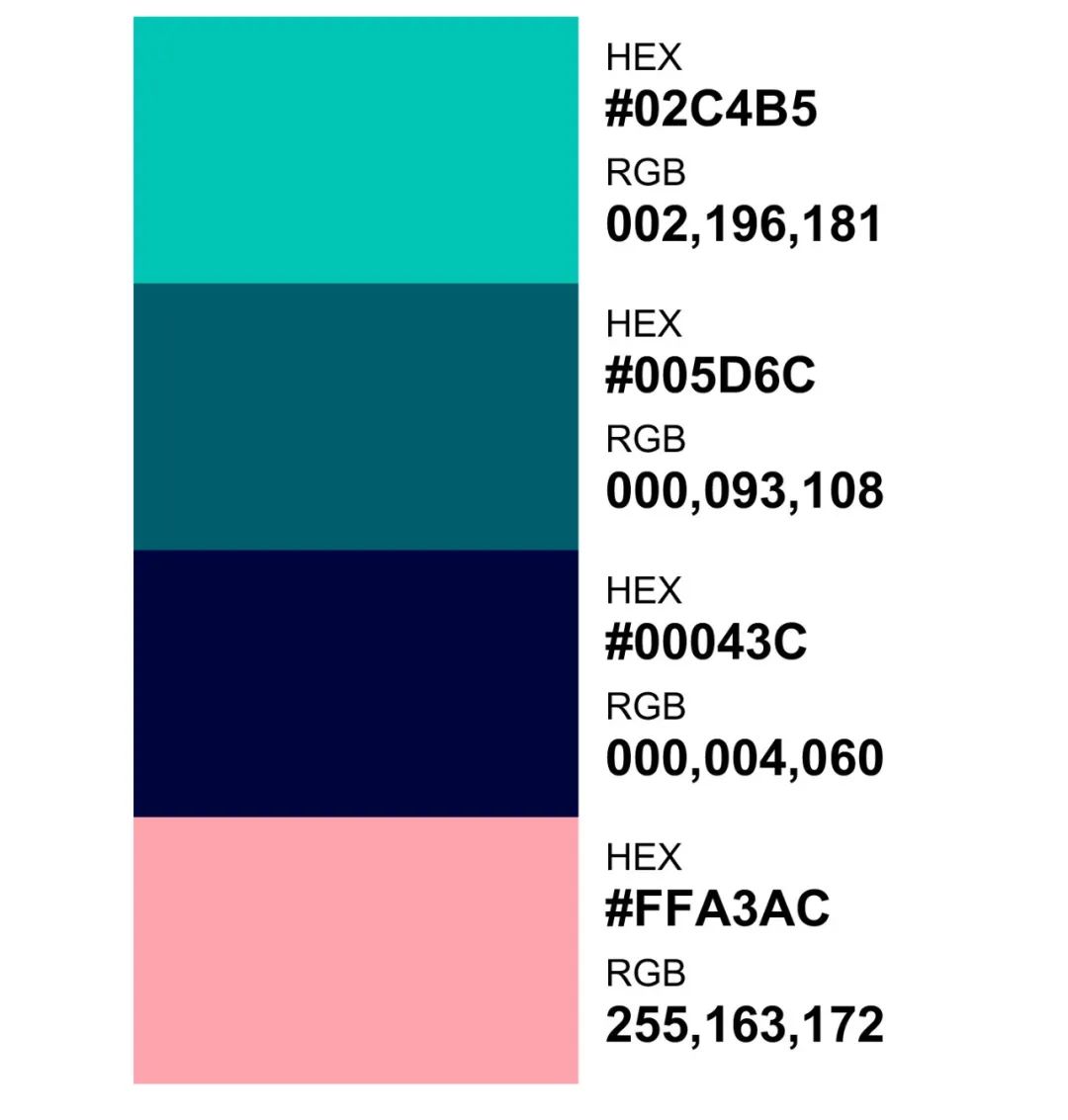
福利!这两款我自制的免费配色工具你领到了吗?
前两天刚入职,还没干过啥活儿,就迎来了中秋3天国庆7天总共8天的假期,美滋滋。 在这么喜庆的日子里,我觉得大家应该也无心科研,所以不如给大家发点儿福利,继续乐呵乐呵。 当然,说是福利&…...

Docker 网桥、docker0 网桥和 --net host:平台差异、使用方式和场景介绍简介:
Docker 是一个流行的容器化平台,它提供了不同的网络配置选项。其中,Docker 网桥、docker0 网桥和 --net host 是常见的网络部署方式。本文将介绍这些网络选项的平台差异、使用方式以及适用的场景。 Docker 网桥 (Bridge Networking):Docker 网桥是 Docker 默认的网络模式。在…...

【深度学习】系统架构工具链的学习笔记
1. 数据管理 数据版本控制和数据包管理:Activeloop Note: Scale Nucleus:其GitHub(nucleus-python-client)的stars数量少于 Deep Lake。Quilt:其GitHub(quilt)的stars数量少于 Deep Lake。...

Linux 网络编程
套接字(Socket): 通过网络实现跨机通信 作用:一种文件描述符传输层的文件描述符 整个编程中,需要着重注意htonl/htons、ntohl/ntohs、inet_addr等 TCP的C/S实现 循环服务器模型 TCP服务器实现过程 1.创建套接字&a…...
SpringBoot读取配置的方式
在 Spring Boot 应用中,我们通常需要一些配置信息来指导应用的运行。这些配置信息可以包括如下内容:端口号、数据库连接信息、日志配置、缓存配置、认证配置、等等。Spring Boot 提供了多种方式来读取这些配置信息。读取配置的目的是为了在程序中使用这些…...

c# winform程序,DispatcherTimer被调用延迟,响应间隔长
c# winform程序,DispatcherTimer被调用延迟,响应间隔长 最近修改的问题,winform界面上两个控件的数据刷新,用DispatcherTimer定时刷新,但是在某些机器上的实际刷新时间间隔远远大于设置时间。 既然MSDN已经说了&…...
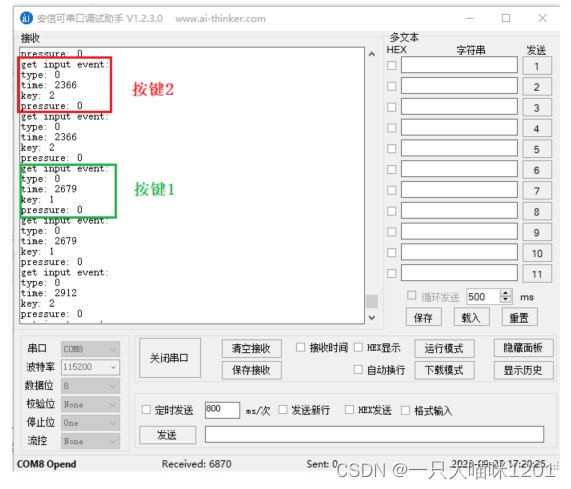
【智能家居项目】裸机版本——项目介绍 | 输入子系统(按键) | 单元测试
🐱作者:一只大喵咪1201 🐱专栏:《智能家居项目》 🔥格言:你只管努力,剩下的交给时间! 目录 🏀项目简介🏀输入子系统(按键)⚽应用层⚽设备层⚽ 内核层抽象层⚽…...

算法练习8——有序三元组中的最大值
LeetCode 100088 有序三元组中的最大值 I LeetCode 100086 有序三元组中的最大值 II 给你一个下标从 0 开始的整数数组 nums 。 请你从所有满足 i < j < k 的下标三元组 (i, j, k) 中,找出并返回下标三元组的最大值。如果所有满足条件的三元组的值都是负数&am…...

git创建
问: git remote add origin https://github.com//blog.git fatal: not a git repository (or any of the parent directories): .git 回答: 这个错误提示指出当前目录或其父目录中不存在.git文件夹,因此无法执行git相关操作。请确保你是在一个已经初始化为git仓库…...

yolov8 opencv模型部署(python版)
yolov8 opencv模型部署(python版) 使用opencv推理yolov8模型,以yolov8n为例子,一共几十行代码,没有废话,给出了注释,从今天起,少写一行代码,少掉一根头发。测试数据有需…...
Simulink仿真封装中的参数个对话框设置
目录 参数和对话框窗格 初始化窗格 文档窗格 为了更加直观和清晰的分析仿真,会将多个元件实现的一个功能封装在一起,通过参数对话框窗格,可以使用参数、显示和动作选项板中的对话框控制设计封装对话框。如图所示: 参数和对话框…...
重载iostream运算符)
【C++】class的设计与使用(十)重载iostream运算符
希望对某个类对象进行读写操作,直接cout<<类对象<<endl;或cin>>类对象;编译器会报错,所以我们必须提供一份重载的input/output运算符: 重载ostream运算符 ostream& operator<<(ostream &os, const Triangu…...

Java使用Scanner类实现用户输入与交互
概述: Scanner类是Java中的一个重要工具类,用于读取用户的输入。它提供了一系列的方法,可以方便地读取不同类型的数据,如整数、浮点数、字符串等。在本文中,我们将详细介绍Scanner类的使用方法,并通过两个…...

FFmpeg 命令:从入门到精通 | ffppeg 命令参数说明
FFmpeg 命令:从入门到精通 | ffmpeg 命令参数说明 FFmpeg 命令:从入门到精通 | ffmpeg 命令参数说明主要参数音频参数视频参数更多参考 FFmpeg 命令:从入门到精通 | ffmpeg 命令参数说明 本节主要介绍了 ffmpeg 命令的常用参数。 主要参数 …...
Chrome(谷歌浏览器)如何关闭搜索栏历史记录
目录 问题描述解决方法插件解决(亲测有效)自带设置解决步骤首先打开 地址 输入:chrome://flags关闭浏览器,重新打开Chrome 发现 已经正常 问题描述 Chrome是大家熟知的浏览器,但是搜索栏的历史记录如何自己一条条的删…...

基于Java的宠物医院管理系统设计与实现(源码+lw+部署文档+讲解等)
文章目录 前言具体实现截图论文参考详细视频演示为什么选择我自己的网站自己的小程序(小蔡coding)有保障的售后福利 代码参考源码获取 前言 💗博主介绍:✌全网粉丝10W,CSDN特邀作者、博客专家、CSDN新星计划导师、全栈领域优质创作…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

在 Spring Boot 项目里,MYSQL中json类型字段使用
前言: 因为程序特殊需求导致,需要mysql数据库存储json类型数据,因此记录一下使用流程 1.java实体中新增字段 private List<User> users 2.增加mybatis-plus注解 TableField(typeHandler FastjsonTypeHandler.class) private Lis…...

前端中slice和splic的区别
1. slice slice 用于从数组中提取一部分元素,返回一个新的数组。 特点: 不修改原数组:slice 不会改变原数组,而是返回一个新的数组。提取数组的部分:slice 会根据指定的开始索引和结束索引提取数组的一部分。不包含…...

渗透实战PortSwigger靶场:lab13存储型DOM XSS详解
进来是需要留言的,先用做简单的 html 标签测试 发现面的</h1>不见了 数据包中找到了一个loadCommentsWithVulnerableEscapeHtml.js 他是把用户输入的<>进行 html 编码,输入的<>当成字符串处理回显到页面中,看来只是把用户输…...

机器学习的数学基础:线性模型
线性模型 线性模型的基本形式为: f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法,得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...

2025年- H71-Lc179--39.组合总和(回溯,组合)--Java版
1.题目描述 2.思路 当前的元素可以重复使用。 (1)确定回溯算法函数的参数和返回值(一般是void类型) (2)因为是用递归实现的,所以我们要确定终止条件 (3)单层搜索逻辑 二…...
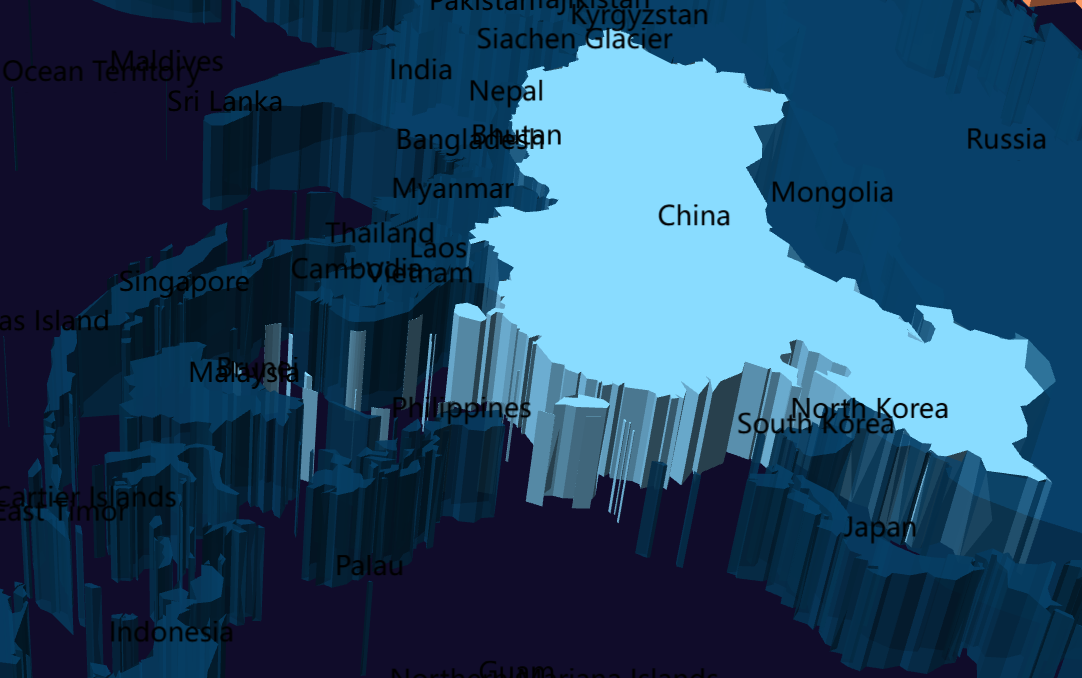
数据可视化交互
目录 【实验目的】 【实验原理】 【实验环境】 【实验步骤】 一、安装 pyecharts 二、下载数据 三、实验任务 实验 1:AQI 横向对比条形图 代码说明: 运行结果: 实验 2:AQI 等级分布饼图 实验 3:多城市 AQI…...
