leetcode之打家劫舍
leetcode 198 打家劫舍
leetcode 213 打家劫舍 II
leetcode 337. 打家劫舍 III
你是一个专业的小偷,计划偷窃沿街的房屋,每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈 ,这意味着第一个房屋和最后一个房屋是紧挨着的。同时,相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警 。
给定一个代表每个房屋存放金额的非负整数数组,计算你 在不触动警报装置的情况下 ,今晚能够偷窃到的最高金额。
示例 1:
输入:nums = [2,3,2]
输出:3
解释:你不能先偷窃 1 号房屋(金额 = 2),然后偷窃 3 号房屋(金额 = 2), 因为他们是相邻的。
示例 2:
输入:nums = [1,2,3,1]
输出:4
解释:你可以先偷窃 1 号房屋(金额 = 1),然后偷窃 3 号房屋(金额 = 3)。
偷窃到的最高金额 = 1 + 3 = 4 。
示例 3:
输入:nums = [1,2,3]
输出:3
提示:
1 <= nums.length <= 100
0 <= nums[i] <= 1000
思路,对于打家劫舍 I, 可以转化成动态规划问题求解,对于打家劫舍 II ,首尾认为是相邻,可以转换成调用 打家劫舍 I 中的问题两次,
class Solution:def maxMoney(self, nums):## dp[i][0] 表示到第 i 位置为止,不偷 i 的最大金额,dp[i][1] 表示偷 i 的最大金额dp = [[0, 0] for i in range(len(nums))]dp[0][1] = nums[0]for i in range(1, len(nums)):dp[i][0] = max(dp[i-1][0], dp[i-1][1])dp[i][1] = dp[i-1][0]+nums[i]return max(dp[-1][0], dp[-1][1])def rob(self, nums: List[int]) -> int:if len(nums) == 1:return nums[0]return max(self.maxMoney(nums[:-1]), self.maxMoney(nums[1:]))
打家劫舍 III, 定义字段 a 和 b,分表表示 盗取(不盗取) 以 当前 root 节点为根节点的最大金额,这样递归就能求解出来。
# Definition for a binary tree node.
# class TreeNode:
# def __init__(self, val=0, left=None, right=None):
# self.val = val
# self.left = left
# self.right = right
class Solution:def __init__(self):self.a = dict() ## 存放以某个节点为根节点能盗取的最高金额(偷根节点)self.b = dict() ## 存放以某个节点为根节点能盗取的最高金额(不偷根节点)## f 为 1 时, 表示偷 root 节点, 为 0 表示不偷def dfs(self, root, f):if root == None:return 0res = 0left_0 = self.b[root.left] if root.left in self.b else self.dfs(root.left, 0)right_0 = self.b[root.right] if root.right in self.b else self.dfs(root.right, 0)left_1 = self.a[root.left] if root.left in self.a else self.dfs(root.left, 1)right_1 = self.a[root.right] if root.right in self.a else self.dfs(root.right, 1)res_0 = max(left_0, left_1) + max(right_0, right_1) ## 不偷 root 节点res_1 = root.val + left_0 + right_0 ## 偷 root 节点self.a[root] = res_1self.b[root] = res_0if f == 1:return res_1else:return res_0def rob(self, root: Optional[TreeNode]) -> int:return max(self.dfs(root, 0), self.dfs(root, 1))相关文章:

leetcode之打家劫舍
leetcode 198 打家劫舍 leetcode 213 打家劫舍 II leetcode 337. 打家劫舍 III 你是一个专业的小偷,计划偷窃沿街的房屋,每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈 ,这意味着第一个房屋和最后一个房屋是紧挨着的。同时&#…...

走进Spring的世界 —— Spring底层核心原理解析(一)
文章目录 前言一、Spring中是如何创建一个对象二、Bean的创建过程三、推断构造方法四、AOP大致流程五、Spring事务 前言 ClassPathXmlApplicationContext context new ClassPathXmlApplicationContext("config.xml"); UserService userService (UserService) cont…...
快看看你的手机有没有:谷歌Android全面封杀此类软件!
谷歌坐不住了,因为Android应用商店中,充斥着大量可窃取用户数据的应用,所以必然要出手整治了。 一款名叫“SonicSpy”软件是整个事情的导火索,而该应用是典型的窃取用户数据的应用,其除了可以从手机中提取个人数据外&…...
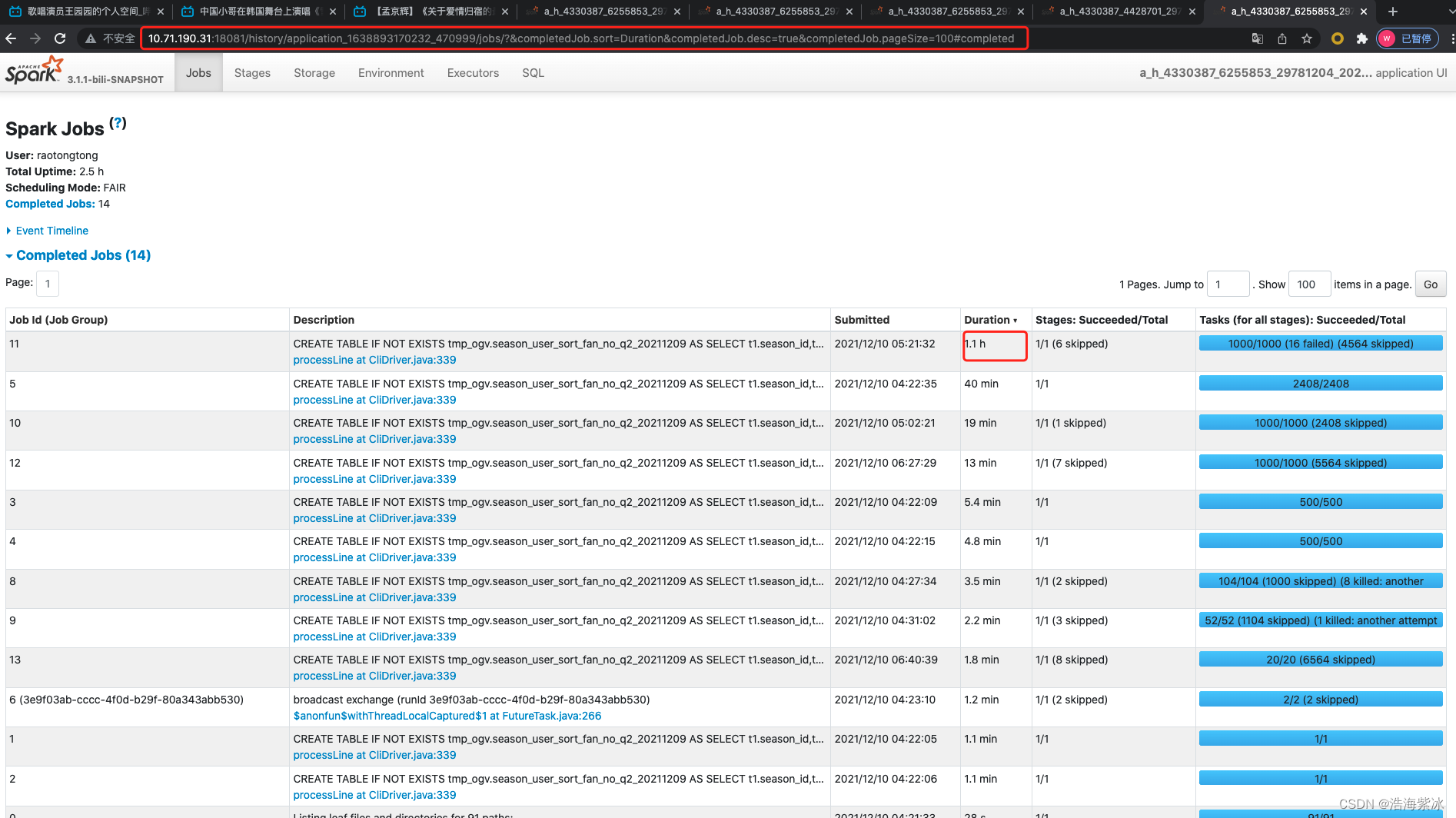
spark ui 指南
spark ui 指南 1.sparkUI 基本介绍2.jobs页面3.stages 页面4.storage 页面5.environment 页面6.ececutor 页面7 sql 页面 spark ui 是反应一个spark 作业执行情况的页面,通过查看作业的执行情况,分析作业运行的状态. 1.sparkUI 基本介绍 进入运行主页面如下,主要有6各部…...
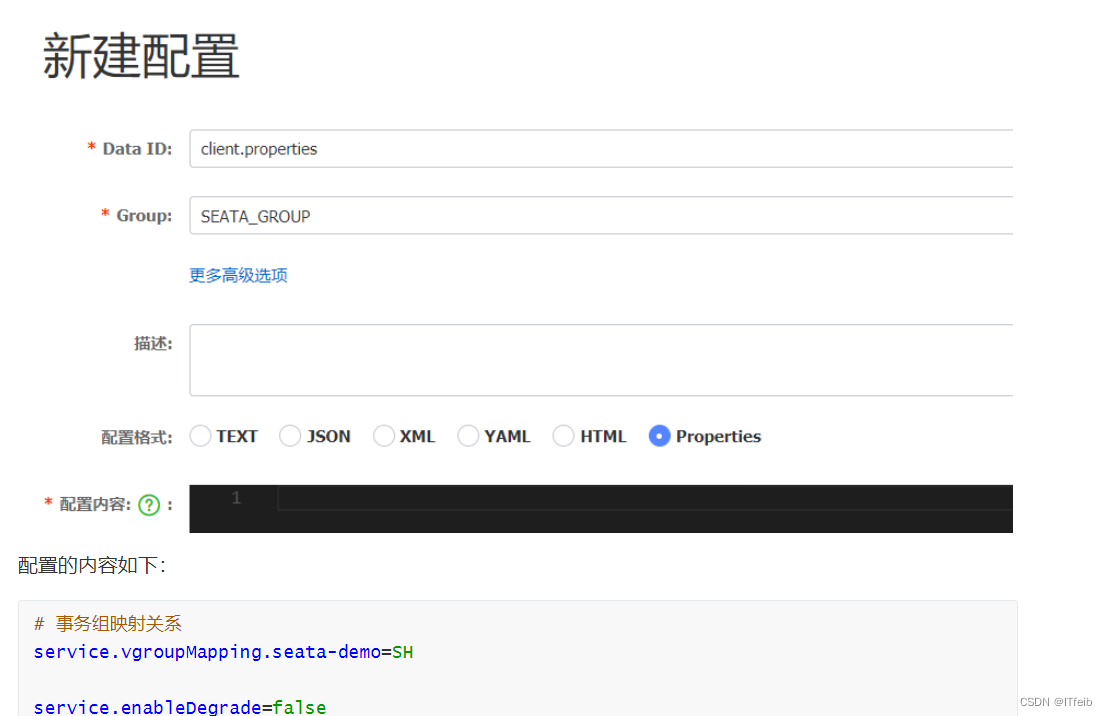
【分布式事务】
文章目录 解决分布式事务的思路seata四种模式1. XA模式2. AT模式AT模式与XA模式的区别是什么?脏写问题 3. TCC模式事务悬挂和空回滚 4. SAGA模式 四种模式对比口述AT模式与TCC模式高可用 什么是分布式事务? 分布式事务,就是指不是在单个服务或…...
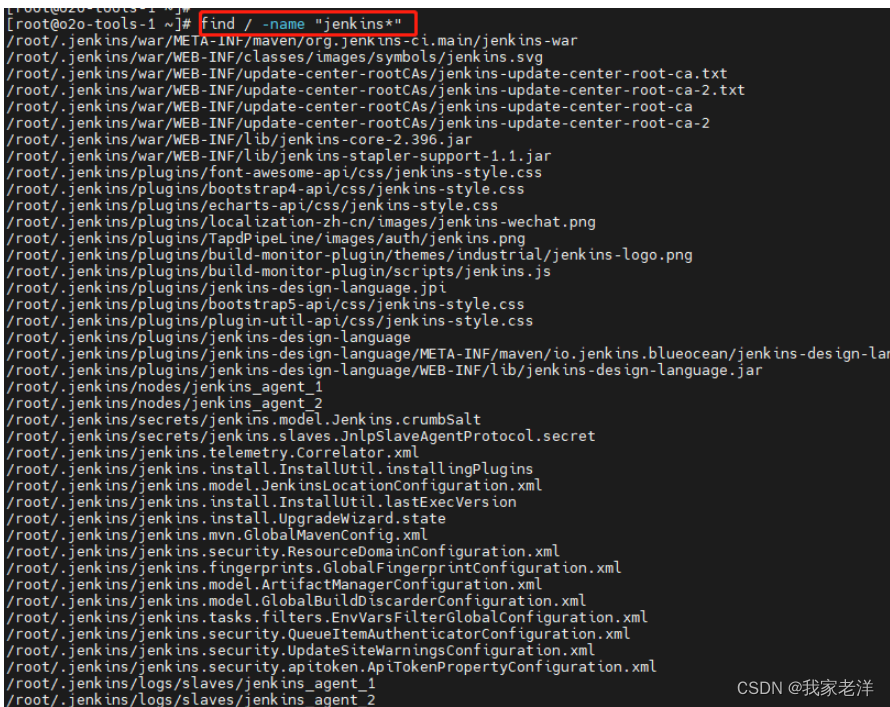
linux 清除卸载jenkins
1、停服务进程 查看jenkins服务是否在运行,如果在运行,停掉 查看服务 ps -ef|grep jenkins 停掉进程 kill -9 XXX2、查找安装目录 find / -name "jenkins*"3、删掉相关目录 删掉相关安装目录 rm -rf /root/.jenkins/# 删掉war包 rm -rf /…...
番外4:VMware安装
step4: 安装过程中,有些选项不需要点(安装地址建议选C盘或默认,装载在其他盘后续会报错),如: may error(本人猜测安装虚拟机完整版需要C盘的一些桥插件支持): step5: 安装虚拟机成功…...

Oracle 19.20 patch 注意事项
1. 打patch 用root 打 /u01/app/19.0.0/grid/OPatch/opatchauto apply /u01/app/patch/35319490 2.打patch 之前 所有NODE上OPatch 版本要一样 3. OPatch 目录不要是root权限 4.打一台,一台自动重启。 有几个node 在几个node 打。patch 都要传到不同的node上 …...
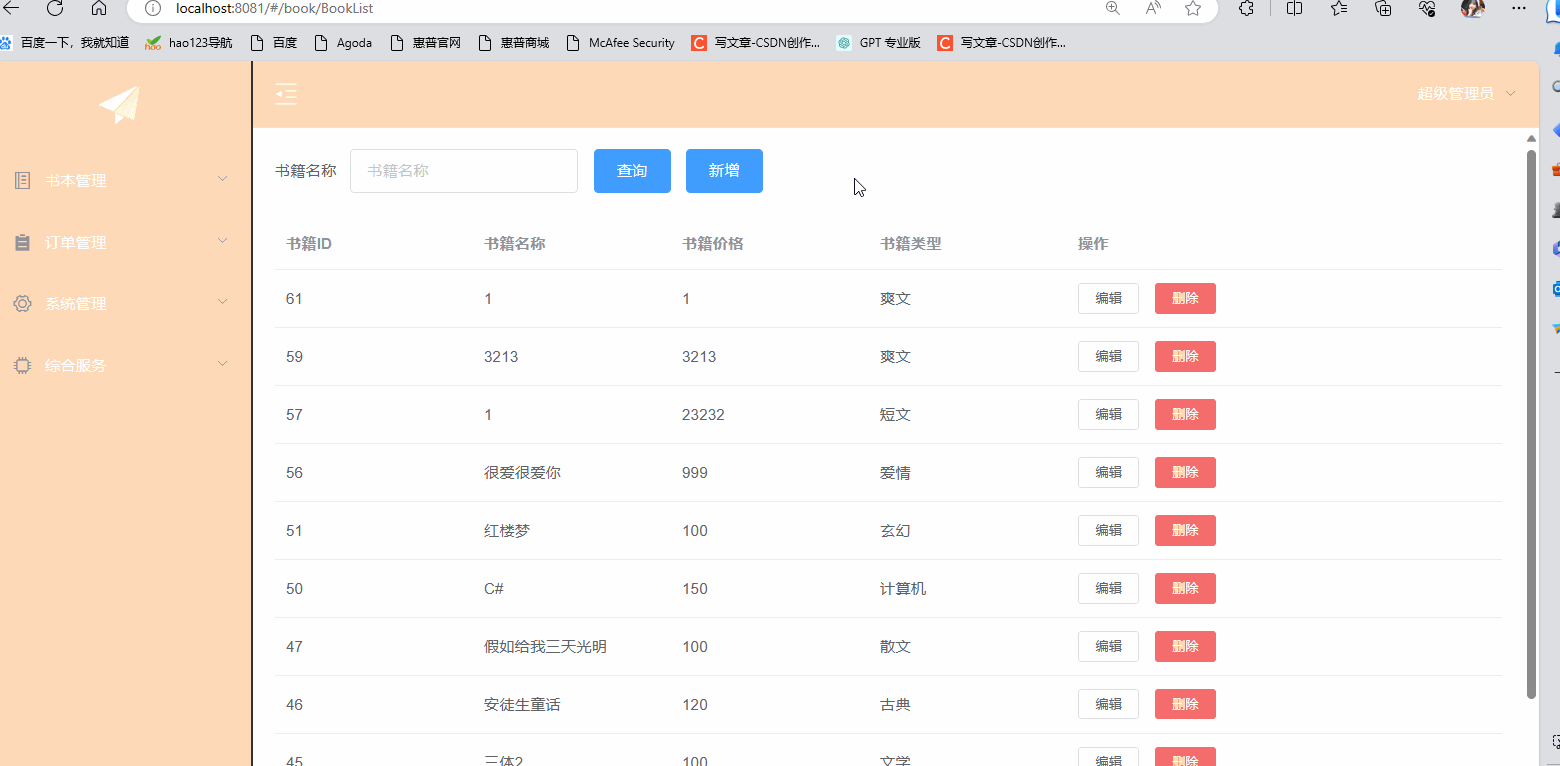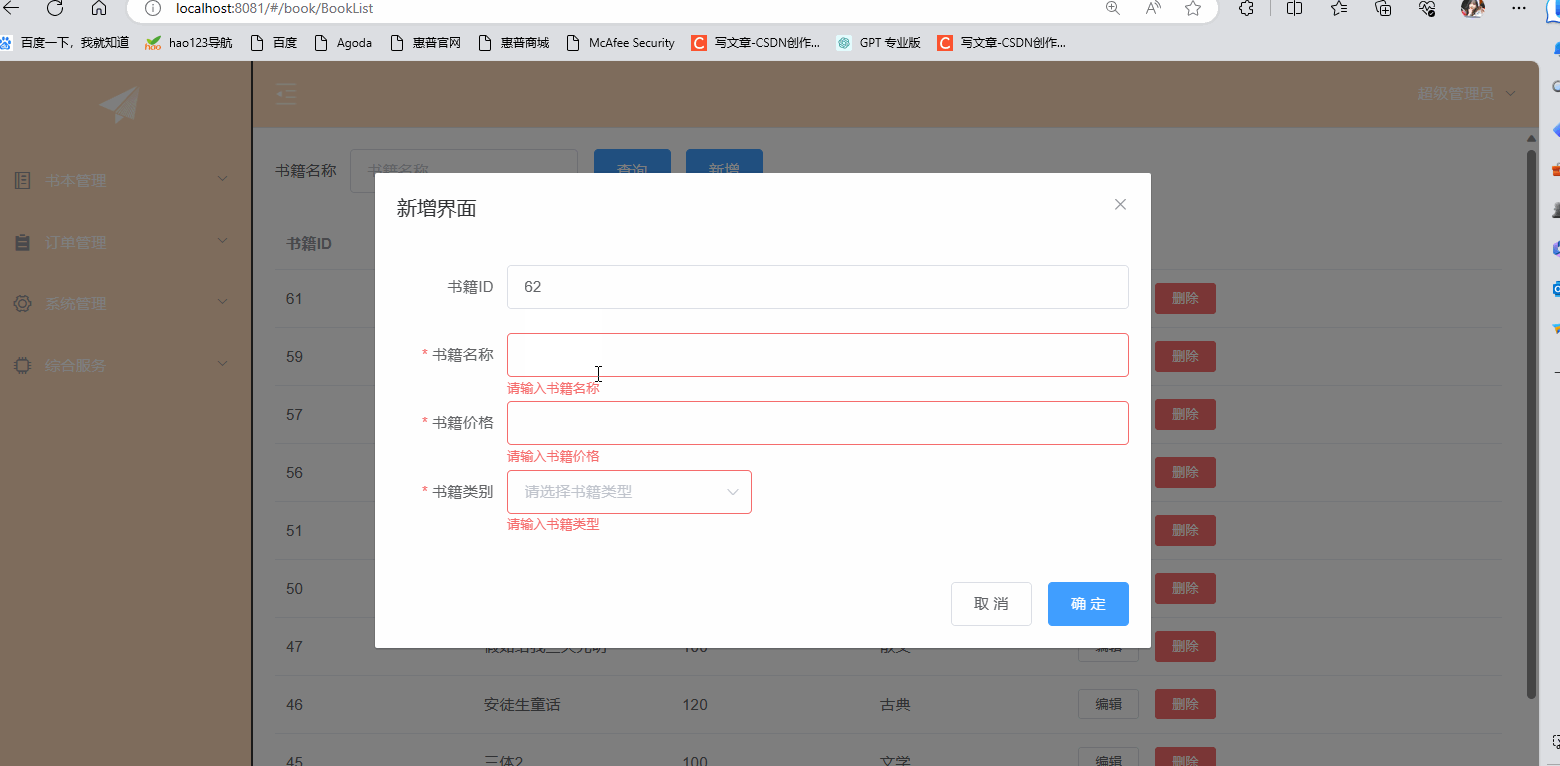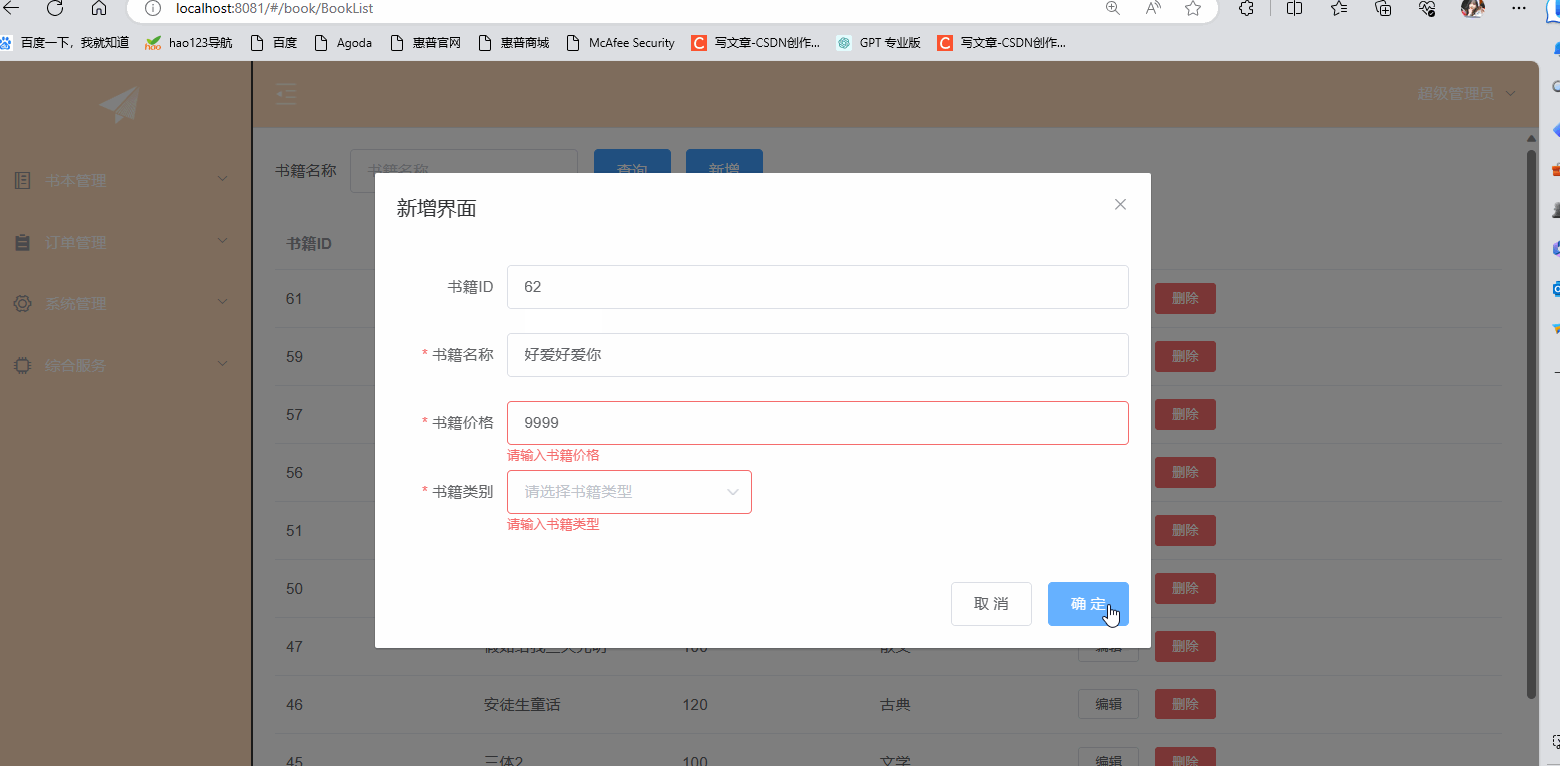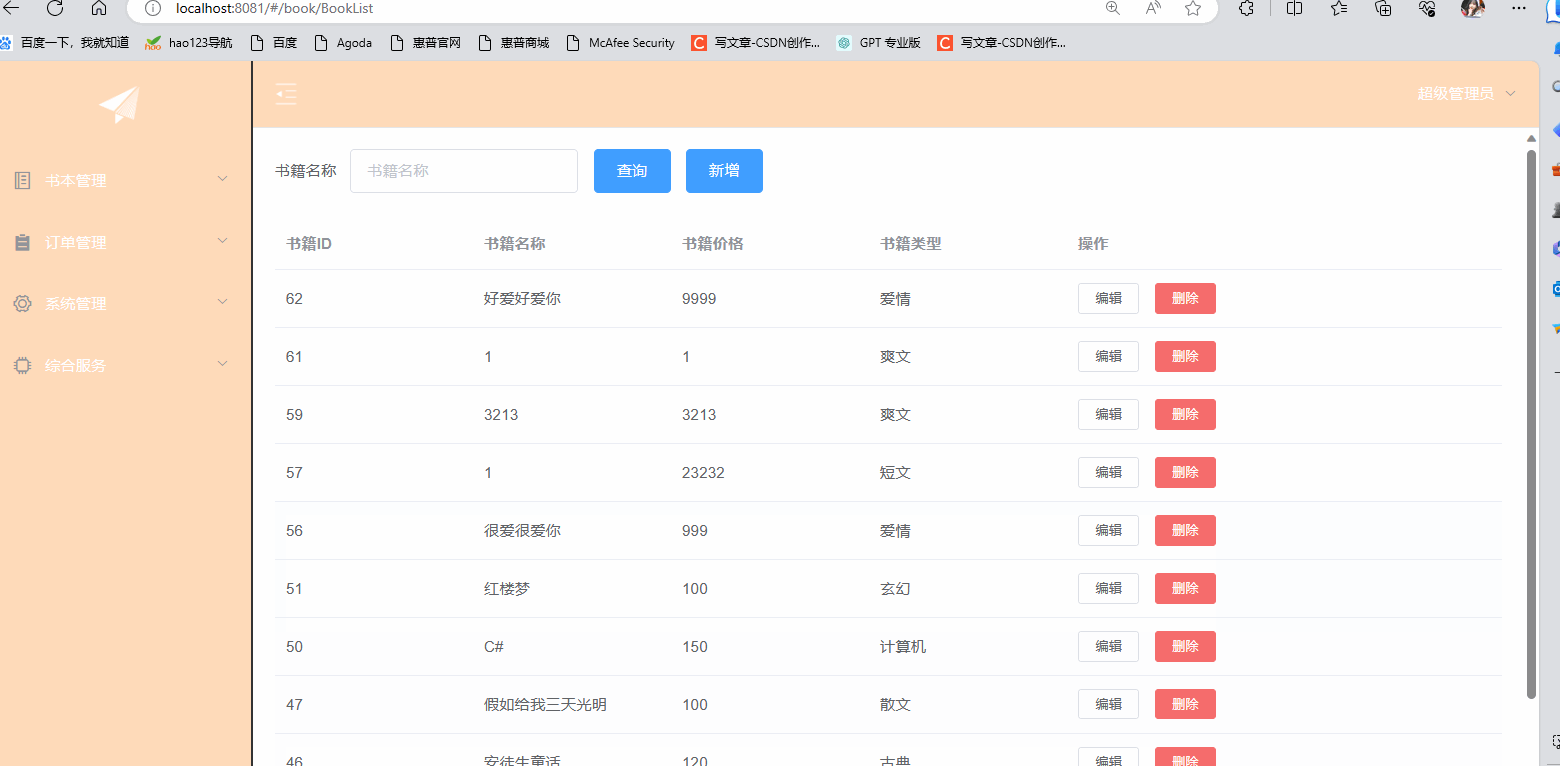
ElementUI之增删改及表单验证
⭐⭐本文章收录与ElementUI原创专栏:ElementUI专栏 ⭐⭐ ElementUI的官网:ElementUI官网 目录 一.前言 二.使用ElementUI完成增删改 2.1 后台代码 2.2 前端代码 三.使用ElementUI完成表单验证 一.前言 本章是继上一篇的基础之上在做完善࿰…...

【Java 进阶篇】深入理解 JDBC:Java 数据库连接详解
数据库是现代应用程序的核心组成部分之一。无论是 Web 应用、移动应用还是桌面应用,几乎都需要与数据库交互以存储和检索数据。Java 提供了一种强大的方式来实现与数据库的交互,即 JDBC(Java 数据库连接)。本文将深入探讨 JDBC 的…...

Web开发-session介绍
目录 session介绍session使用场景session具体使用需要注意的是 session介绍 session 可以被看作是一种缓冲区,用于在多个请求之间存储和传递用户数据。在 Web 应用程序中,session 通常用于存储用户登录信息、购物车数据、用户偏好设置等。当用户在应用程…...

基于Qt Creator开发的坦克大战小游戏
目录 介绍开发环境技术介绍安装说明项目目录设计思想项目介绍运行演示知识点记录Gitee源码链接 介绍 !!!资源图片是从网上免费下载,源码都是原创,供个人学习使用,非盈利!!ÿ…...
小说推文和短剧推广以及电影达人带货电影票
小说推文、短剧推广、电影达人(带或电影票)都可以通过“巨量推文“进行申请授权 小说推文和短剧推广是什么? 小说推文和短剧推广的逻辑其实一样,分为cpa拉新和cps分成的推广形式 cpa拉新是你推广的用户必须为新用户,…...
:数据挖掘十大算法之一)
朴素贝叶斯分类(下):数据挖掘十大算法之一
⭐️⭐️⭐️⭐️⭐️欢迎来到我的博客⭐️⭐️⭐️⭐️⭐️ 🐴作者:秋无之地 🐴简介:CSDN爬虫、后端、大数据领域创作者。目前从事python爬虫、后端和大数据等相关工作,主要擅长领域有:爬虫、后端、大数据开发、数据分析等。 🐴欢迎小伙伴们点赞👍🏻、收藏⭐️、…...

9.30作业
C语言基础考题(40) 选择题 20分每题2分 1、已知字母A的ASCII码为十进制数值65,且S为字符型,则执行语句SA6-3;后S中的值为 ( ) A.D B.68 C.不确定的值 D.C 2、若有定义语句:int a12;,则执…...

[GWCTF 2019]枯燥的抽奖
参考 https://www.cnblogs.com/AikN/p/15764428.html [GWCTF 2019]枯燥的抽奖-CSDN博客 打开环境 笑死我了,怎么那么像我高中校长 查看源代码 看到check.php,去访问一下 ok看到源代码了 因为上次做过,看到这个我就想到用php_mt_seed逆推…...

vue3中sync修饰符的使用
props是子组件与父组件进行通信的常用方式,使用步骤主要有以下几个: 1. 在子组件中定义props要从父组件接收的变量(变量的类型必须写明,默认值可选) // 这里以 document.vue 子组件为例 // 通过 defineProps 宏的方…...

Qt全屏显示与退出
仿照 按Escape键退出程序中的实现,我们在程序开始的时候全屏显示,按esc键的时候退出全屏。 showFullScreen 全屏显示只需要调用QWidget类(QMainWindow也是一个QWidget类)的 showFullScreen() 成员函数即可。 退出全屏&#x…...

OpenCV之直线曲线拟合
直线拟合fitLine void fitLine( InputArray points, OutputArray line, int distType,double param, double reps, double aeps ); points:二维点的数组或vector line:输出直线,Vec4f (2d)或Vec6f (3d)的vector distType:距离类型 param:距离参数 reps:径向的精度参数 a…...

2023年哪款PDF虚拟打印机好用?
PDF文档想必大家都不陌生,在工作中经常会用到该格式的文档,那么有哪些方法能制作PDF文档呢?一般都是借助PDF虚拟打印机的,那么有哪些好用的软件呢? pdfFactory不仅为用户提供了丰富的PDF文档生成、打印功能࿰…...

HTML 语义化
目录 HTML 语义化HTML5 新特性HTML 语义化的好处语义化标签的使用场景最佳实践 HTML 语义化 HTML5 新特性 标准答案: 语义化标签: <header>:页头<nav>:导航<main>:主要内容<article>&#x…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

2.Vue编写一个app
1.src中重要的组成 1.1main.ts // 引入createApp用于创建应用 import { createApp } from "vue"; // 引用App根组件 import App from ./App.vue;createApp(App).mount(#app)1.2 App.vue 其中要写三种标签 <template> <!--html--> </template>…...
)
postgresql|数据库|只读用户的创建和删除(备忘)
CREATE USER read_only WITH PASSWORD 密码 -- 连接到xxx数据库 \c xxx -- 授予对xxx数据库的只读权限 GRANT CONNECT ON DATABASE xxx TO read_only; GRANT USAGE ON SCHEMA public TO read_only; GRANT SELECT ON ALL TABLES IN SCHEMA public TO read_only; GRANT EXECUTE O…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...

nnUNet V2修改网络——暴力替换网络为UNet++
更换前,要用nnUNet V2跑通所用数据集,证明nnUNet V2、数据集、运行环境等没有问题 阅读nnU-Net V2 的 U-Net结构,初步了解要修改的网络,知己知彼,修改起来才能游刃有余。 U-Net存在两个局限,一是网络的最佳深度因应用场景而异,这取决于任务的难度和可用于训练的标注数…...
