思维模型 周期
本系列文章 主要是 分享 思维模型,涉及各个领域,重在提升认知。周期是一个看似极为简单,但背后却蕴藏着大智慧的模型,了解周期,对于了解王朝更替,数学之美,经济运转等都有帮助。
1 周期的应用
1.1 生活中常见的周期
- 日夜周期:地球的自转导致了白天和黑夜的交替。
- 四季周期:地球绕太阳公转导致了春、夏、秋、冬四季的交替。
- 月相周期:月球围绕地球运转,导致了月相的变化,如新月、上弦月、满月和下弦月。
- 潮汐周期:潮汐是由太阳和月球的引力引起的,导致海水的周期性上升和下降。
- 生命周期:生物有自己的生命周期,包括出生、成长、繁殖和死亡阶段。
- 经济周期:经济领域存在周期性的繁荣、衰退、复苏和衰退阶段。
- 社会周期:社会变迁和文化发展也有自己的周期,如时代的交替和文化的变革。
- 人类生活周期:个体人的生命周期包括婴儿、儿童、青少年、成年人和老年人阶段。
- 天文周期:天文学中存在各种周期性事件,如彗星的周期性出现、行星的合和分等。
- 自然生态周期:生态系统中存在各种生态周期,如植物的生长季节、动物的迁徙季节等。
- 王朝的更替:比如当一个朝代达到鼎盛时,政治稳定、社会繁荣;但随着时间的推移,一定会出现统治者的腐败、民生困苦、外敌入侵等问题,最后导致朝代衰落和灭亡。
这些是生活中一些常见的周期,每个周期都有其独特的特征和影响。周期性的事件和现象在我们的日常生活中起着重要的作用,帮助我们理解和适应自然和社会环境的变化。
1.2 数学中的周期函数
周期函数是数学中的一个概念,它是指具有重复性或周期性的特性的函数。这意味着在函数图像上可以找到一个或多个周期,通过这些周期,函数的值会重复出现。周期函数的主要特点包括:
- 周期:周期函数具有一个或多个周期,这是函数值以相同或相似的方式重复的时间或空间间隔。周期通常表示为T。
- 周期性:函数在每个周期内的行为是相似的。这意味着,如果你在一个周期内观察函数的值和图像,然后在下一个周期内进行相同的观察,你会看到相似的模式。
- 正周期函数和负周期函数:如果函数在周期T内重复,那么它是正周期函数。如果函数在周期-T内重复,那么它是负周期函数。
- 周期性函数的例子:正弦函数(sine function)和余弦函数(cosine function)是最常见的周期函数。它们在周期2π内重复。
- 正弦函数:f(x) = sin(x),其周期是2π。
- 余弦函数:f(x) = cos(x),其周期也是2π。
- 周期延伸:某些周期函数可以在一个周期内延伸到更长的时间或更广的空间范围。这可以通过改变函数的振幅、频率或相位来实现。
周期函数在数学、物理、工程等领域中具有广泛的应用。它们用于描述许多周期性现象,如声波、电信号、天文运动、机械振动等。通过研究周期函数的性质,我们可以更好地理解和预测这些现象。
1.3 软件开发中的周期
软件开发周期是指将一个软件项目从概念到最终交付和维护的整个过程,它通常包括以下基本阶段:
- 需求分析:在这个阶段,开发团队与客户或用户合作,收集并明确定义软件项目的需求和目标。这包括确定系统功能、性能、安全性、用户体验等方面的要求。
- 设计:在需求分析的基础上,开发团队制定软件系统的设计方案。这包括定义系统架构、数据库设计、用户界面设计和数据流程等。设计文档通常会详细描述软件的结构和组成部分。
- 开发:一旦设计完成,开发团队开始编写实际的代码,实现软件系统的各个组件和功能。这是将概念转化为实际软件的阶段。
- 测试:在开发完成后,软件需要经过一系列的测试,包括单元测试、集成测试和系统测试,以确保其功能正常运作、性能满足要求,并且没有明显的错误或问题。
- 部署:在经过测试和验收后,软件准备好部署到生产环境中。这包括安装、配置和确保软件在用户环境中正常运行。
- 维护和支持:软件部署后并不意味着开发结束。开发团队需要继续监控软件的性能、稳定性,并解决可能出现的问题、错误或漏洞。此外,还需要对软件进行定期的更新和维护,以适应新的需求或技术变化。
- 文档和管理:在整个开发周期中,项目管理、文档编写和团队协作也是关键的。管理团队负责项目的进度和资源分配,而文档用于记录需求、设计、测试结果以及用户手册等。
- 交付和验收:最终,软件项目交付给客户或用户,经过验收测试以确保其符合预期的质量标准和功能需求。
软件开发周期可以采用不同的方法和模型,如瀑布模型、敏捷开发、迭代开发等,每种模型都可能会对生命周期的阶段和顺序进行不同的调整。选择适合项目需求和团队的开发方法是非常重要的,以确保项目的成功。
特殊说明:流程图中有 顺序、选择、循环单个基石,循环的本质即为事物周期规律的呈现。
1.4 统计学中的季节因素
统计学中的季节因素是指随着时间的推移,数据中出现的重复性和周期性变化。这种变化通常与季节、月份、星期几或其他时间单位有关。季节因素在统计分析中很重要,因为它们可以揭示出数据中与时间相关的趋势和模式,有助于更好地理解数据并做出合适的预测或决策。这里以一种形象的方式解读,以帮助理解统计学中的季节因素:假设一家卖冰淇淋的小商店。这家商店记录了每天的销售额,然后将这些数据进行分析。在数据中,他们可能会观察到以下情况:
- 季节性增长:在夏季,冰淇淋销售额显著增加,而在冬季则下降。这是因为夏季天气炎热,人们更愿意购买冰淇淋,而冬季则相反。
- 每周周期性变化:销售额在周末可能比工作日更高。这是因为人们通常在周末休闲时间更多,更有可能去购买冰淇淋。
- 每月周期性变化:每个月的销售额也可能有所不同,可能在月底支付工资时更高,而月初则相对较低。
这些季节性的变化形成了数据中的周期性模式。统计学家可以使用时间序列分析方法来检测和量化这些季节因素,以便更好地预测未来销售额,制定库存策略,或做其他经营决策。
总之,统计学中的季节因素是一种周期性的数据模式,它们帮助我们理解与时间相关的趋势,这对于许多不同领域的数据分析和决策制定都至关重要。
1.5 经济学中的周期
按照周期的长短,经济周期理论可以划分为:
- 短周期(库存周期):英国经济学家基钦提出的一种为期3-4年的经济周期。1923年英国经济学家基钦提出的一种为期3-4年的经济周期。基钦周期也叫库存周期,基钦根据美国和英国1890年到1922年的利率、物价、生产和就业等统计资料从厂商生产过多时就会形成存货、从而减少生产的现象出发,把这种2一4年的短期调整称为“存货”周期,在40个月中出现了有规则的上下波动发现了这种短周期。。
- 中周期,法国经济学家朱格拉提出来的一种9~10年的经济周期。1860年法国经济学家朱格拉提出的一种为期10年左右的经济周期。该周期是以国民收入、失业率和大多数经济部门的生产、利润和价格的波动为标志加以划分的。朱格拉认为,存在着危机或恐慌并不是一种独立的现象,而是社会经济运动三个阶段中的一个,这三个阶段是繁荣、危机与萧条。三个阶段的反复出现就形成了周期现象。
- 长周期,就是康德拉季耶夫提出来的一种50~60年的经济周期,是1926年俄国经济学家康德拉季耶夫提出的一种为期50-60年的经济周期。康波理论即康德拉季耶夫长波周期理论的缩写。也称康波周期。康波的核心观点就是全世界的资源商品和金融市场会按照50-60年为周期进行波动,一个大波里面有4个小波:繁荣、衰退、萧条、回升,也就是美林时钟的理论基础。
- 建筑周期,美国经济学家库涅茨提出来的一种20年左右的经济周期。是1930年美国经济学家库涅茨提出的一种为期15-25年,平均长度为20年左右的经济周期。由于该周期主要是以建筑业的兴旺和衰落这一周期性波动现象为标志加以划分的,所以也被称为“建筑周期”。在全球房地产商品化程度提升之后,房地产业对于库兹涅茨周期影响更大。
2 思维模型 周期
2.1 周期是什么?
周期是指事件、现象、变化或重复出现的模式在一段时间或空间内反复发生的规律。在周期性现象中,某一特定情况或状态以一定的频率重复,然后再次出现,形成可识别的模式。
举例来说,地球绕太阳公转的周期大约是365.25天,这导致了四季的交替。这意味着每年都会经历春、夏、秋、冬四个季节,然后再次回到春季,形成一个年度周期。
周期在许多领域都有重要应用,包括自然科学、数学、经济学和社会科学。通过研究和理解周期性现象,我们可以更好地预测未来事件,制定合理的计划,以及更好地理解世界中的各种变化和规律。
2.2 为什么会有周期现象?
周期现象之所以存在,是因为许多自然和物理过程受到一系列相互关联的因素和力量的影响,这些因素和力量在一段时间或空间内以固定的频率或规律性方式交互作用,导致了周期性变化。以下是一些常见的原因和机制,解释为什么会出现周期现象:
- 自然力和物理定律:许多周期性现象是由自然力和物理定律所驱动的。例如,地球绕太阳的周期是由万有引力定律和牛顿的运动定律所决定的。
- 振动和波动:振动和波动是一种常见的周期性现象。例如,声波是由物体的振动引起的,光波是由电场和磁场的振动引起的。
- 化学反应:某些化学反应具有周期性特性。例如,化学钟反应中,颜色的变化以一定的周期性重复。
- 天文现象:天文现象如日食、月食、星座的位置等都具有周期性。这是因为行星、卫星和恒星的运动是有规律的,它们的位置和相对位置会周期性地变化。
- 气候和季节:气候和季节变化是地球轨道和自转的结果。这些周期性变化导致了四季的交替。
- 人类活动和社会因素:某些周期性现象是由人类活动和社会因素引起的。例如,经济周期受到市场供需、政策和商业活动的影响,导致经济增长和衰退的周期性。
总之,周期现象的存在通常是由于复杂的相互作用和规律性的因素所导致。这些周期性现象在自然界和人类社会中普遍存在,科学家和研究人员研究它们以更好地理解和预测世界中的变化和规律。
3 模型简图

相关文章:

思维模型 周期
本系列文章 主要是 分享 思维模型,涉及各个领域,重在提升认知。周期是一个看似极为简单,但背后却蕴藏着大智慧的模型,了解周期,对于了解王朝更替,数学之美,经济运转等都有帮助。 1 周期的应用 …...

从 0 到 1 ,手把手教你编写《消息队列》项目(Java实现) —— 介绍项目/ 需求分析
文章目录 一、消息队列是什么?二、需求分析结构解析功能解析规则解析绑定关系交换机类型消息应答 三、持久化存储四、网络通信提供的API复用TCP连接 五、消息队列概念图 一、消息队列是什么? 消息队列 (Message Queue, MQ)就是将阻塞队列这一数据结构提取…...
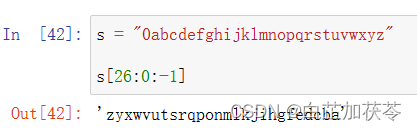
Python学习之索引与切片
Python学习之索引与切片 s “0abcdefghijklmnopqrstuvwxyz”,第一个元素‘0’,索引号为0,最后一个元素‘z’,索引号为26 1. s[0]获取索引号为0的元素 2. s[1:3]获取索引号为1的元素,直到但不包括索引号为3的元素。即…...

编程每日一练(多语言实现)基础篇:满足abcd=(ab+cd)^2的数 (增加Go语言实现)
文章目录 一、实例描述二、技术要点三、代码实现3.1 C 语言实现3.2 Python 语言实现3.3 Java 语言实现3.4 JavaScript 语言实现3.5 Go 语言实现 一、实例描述 假设 abcd 是一个四位整数,将它分成两段,即 ab 和 cd,使之相加求和后再平方。求满…...

LeetCode 热题 HOT 100:回溯专题
LeetCode 热题 HOT 100:https://leetcode.cn/problem-list/2cktkvj/ 文章目录 17. 电话号码的字母组合22. 括号生成39. 组合总和46. 全排列补充:47. 全排列 II (待优化)78. 子集79. 单词搜索124. 二叉树中的最大路径和200. 岛屿数量437. 路径…...

喝健康白酒 有益生心健康
中国的制酒史源远流长,酒渗透在中华五千年的文化中。酒与烟不同,烟对人体有百害而无一利,而对于酒,若掌握好饮酒的度,对人体有一定的养生作用,所以我们通常会说“戒烟限酒”。 据一些专家研究,…...

动态规划:两个数组的dp问题(C++)
动态规划:两个数组的dp问题 前言两个数组的dp问题1.最长公共子序列(中等)2.不同的子序列(困难)3.通配符匹配(困难)4.正则表达式(困难)5.交错字符串(中等&…...

BASH shell脚本篇2——条件命令
这篇文章介绍下BASH shell中的条件相关的命令,包括:if, case, while, until, for, break, continue。之前有介绍过shell的其它基本命令,请参考:BASH shell脚本篇1——基本命令 1. If语句 if语句用于在顺序执行语句的流程中执行条…...

【图论C++】Floyd算法(多源最短路径长 及 完整路径)
>>>竞赛算法 /*** file * author jUicE_g2R(qq:3406291309)————彬(bin-必应)* 一个某双流一大学通信与信息专业大二在读 * * brief 一直在算法竞赛学习的路上* * copyright 2023.9* COPYRIGHT 原创技术笔记ÿ…...
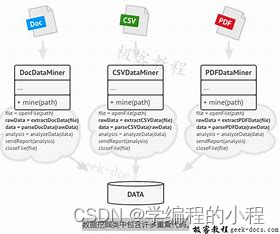
小谈设计模式(11)—模板方法模式
小谈设计模式(11)—模板方法模式 专栏介绍专栏地址专栏介绍 模板方法模式角色分类抽象类(Abstract Class)具体子类(Concrete Class)抽象方法(Abstract Method)具体方法(C…...
C#程序中很多ntdll.dll、clr.dll的线程
如下图 需要“右键工程——调试——取消勾选‘启用本地代码调试’”即可。...

低代码工作流程管理系统:提升企业运营效率的利器
业务运营状况是否良好,除了人员需要配合以外,真正发挥作用的是背后的工作流程。将重复的工作进行自动化处理,确保这些流程最终指向同一个目标、实现一致的运营结果。而设计和实施不佳的工作流程则产生相反的效果——导致处理时间延长、运营成…...

HIVE SQL regexp_extract和regexp_replace配合使用正则提取多个符合条件的值
《平凡的世界》评分不错,《巴黎圣母院》改变成的电影不错,还有<<1984>>也蛮好看。 如何使用regexp_extract®exp_replace函数将以上文本中所有书籍名称都提取出来? select substr(regexp_replace(regexp_extract(regexp_…...

debian 安装matlab2022b报错解决方法与问题解决思路
报错 terminate called after throwing an instance of ‘std::runtime_error’ 在安装目录执行 ./bin/glnxa64/MATLABWindow通过执行以上命令发现是和libharfbuzz库有关。 该库在调用freetype库时,有方法找不到。 偿试remove freetype库,发现该库有大…...

Jenkins集成AppScan实现
一、Jenkins上安装插件 在Jenkins里安装以下插件 ibm-security-appscanstandard-scanner 二、打开AppScan 1、配置需要扫描的地址 配置需要扫描的地址 2、记录好要扫描的URL登录序列 记录好要扫描的URL登录序列 3、导出要扫描的URL登录序列设置 导出要扫描的URL登录序列设置 三…...

10.1 File类
前言: java.io包中的File类是唯一一个可以代表磁盘文件的对象,它定义了一些用于操作文件的方法。通过调用File类提供的各种方法,可以创建、删除或者重命名文件,判断硬盘上某个文件是否存在,查询文件最后修改时间&…...

[论文笔记]UNILM
引言 今天带来论文Unified Language Model Pre-training for Natural Language Understanding and Generation的笔记,论文标题是 统一预训练语言模型用于自然语言理解和生成。 本篇工作提出了一个新的统一预训练语言模型(Unifield pre-trained Language Model,UniLM),可以同…...
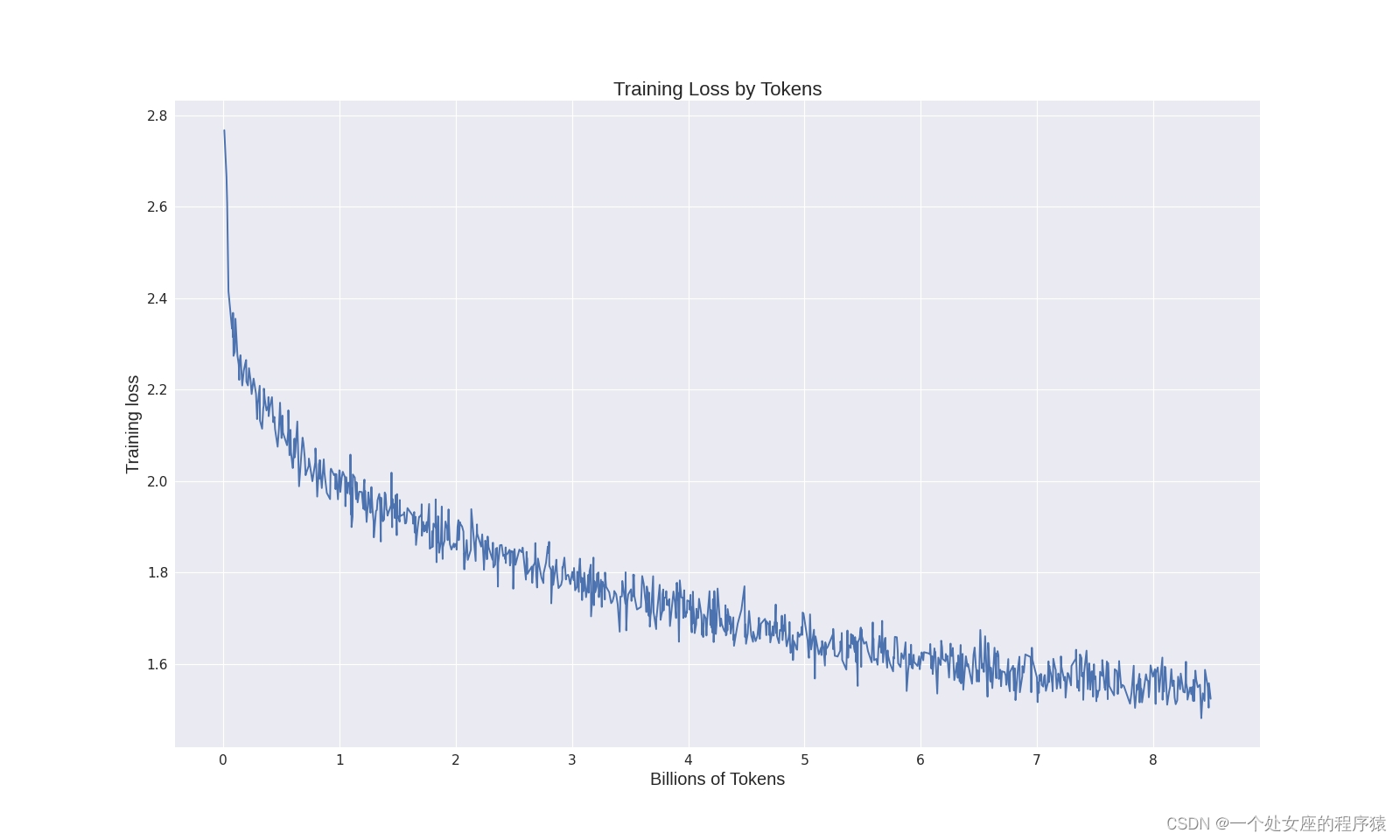
LLM之Colossal-LLaMA-2:Colossal-LLaMA-2的简介、安装、使用方法之详细攻略
LLM之Colossal-LLaMA-2:Colossal-LLaMA-2的简介、安装、使用方法之详细攻略 导读:2023年9月25日,Colossal-AI团队推出了开源模型Colossal-LLaMA-2-7B-base。Colossal-LLaMA-2项目的技术细节,主要核心要点总结如下: >> 数据处…...
国庆作业2
select实现服务器并发 代码: #include <myhead.h>#define ERR_MSG(msg) do{\printf("%d\n",__LINE__);\perror(msg);\ }while(0)#define PORT 8888#define IP "192.168.1.5"int main(int argc, const char *argv[]) {//创建流式套接字…...

fork仓库的代码如何同步主仓库代码
1.背景 我fork了一份 jekyll-theme-chirpy 仓库的代码(基于 jekyll 的自建博客仓库,可以免服务器),我需要在上面更新我的博客文章,但是我又想一直同步 jekyll-theme-chirpy 仓库的新功能,这样我可以更新自己的博客功能。所以我就…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
智慧工地云平台源码,基于微服务架构+Java+Spring Cloud +UniApp +MySql
智慧工地管理云平台系统,智慧工地全套源码,java版智慧工地源码,支持PC端、大屏端、移动端。 智慧工地聚焦建筑行业的市场需求,提供“平台网络终端”的整体解决方案,提供劳务管理、视频管理、智能监测、绿色施工、安全管…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...
