【图论C++】Floyd算法(多源最短路径长 及 完整路径)
>>>竞赛算法
/*** @file * @author jUicE_g2R(qq:3406291309)————彬(bin-必应)* 一个某双流一大学通信与信息专业大二在读 * * @brief 一直在算法竞赛学习的路上* * @copyright 2023.9* @COPYRIGHT 原创技术笔记:转载需获得博主本人同意,且需标明转载源** @language C++* @Version 1.0还在学习中 */
- UpData Log👆 2023.9.29 更新进行中
- Statement0🥇 一起进步
- Statement1💯 有些描述可能不够标准,但能达其意
文章目录
- >>>竞赛算法
- 21 Floyd算法
- 21-1 比较几种求解 最短路径 的算法
- 21-2 孕育出 Floyd算法 的 原因
- 21-3 Floyd算法 的 实现
- 就纯一暴力法,没什么说的
21 Floyd算法
21-1 比较几种求解 最短路径 的算法
- 常见的有:
DJ算法、Floyd算法、A*算法、Bellman-Ford 算法、SPFA算法
其中 A*算法 是 DJ算法 的plus版,SPFA算法 是 Bellman-Ford 算法的plus版
| 算法名称 | DJ算法 | Floyd算法 | SPFA算法 | A*算法 |
|---|---|---|---|---|
| 单/多源 | 单源 | 多源 | 单源 | |
| 可否求负权值图 | 否 | 可 | 否 | |
| 效率 | 较高 | 较低 | 很高 | |
| 思想 | 贪心 | 动规DP,松弛 | 松弛 | 启发式搜索,估值函数 |
| 解的最优性 | 最优 | 最优 | 相对最优 |
- 单源指的是:一个起点,到其他所有点
21-2 孕育出 Floyd算法 的 原因
求 n个端点的图 的 多源最短路径,可以将 Dijkstra算法 执行 n次,但这样时间复杂度也上去了 O ( n 2 ∗ n ) O(n^2*n) O(n2∗n),而且代码也很臃肿,此时就需要针对这类问题单独设计一种算法解决 代码量大 的问题——就产生了Floyd算法 。
虽然 Floyd算法 的效率相对较低 1 ^1 1且不适合处理数据量过大 2 ^2 2的图 ,但是它处理 稠密图 3 ^3 3 时效率是高于 Dijkstra算法的,而且 floyd算法 的代码量极小 4 ^4 4,实现也很简单!!!
1 ^1 1:时间复杂度为 O ( n 3 ) O(n^3) O(n3)。
2 ^2 2:空间复杂度为 O ( n 2 ) O(n^2) O(n2):,使用的是邻接矩阵(直接开辟二维数组)。在处理
稠密图时格外浪费空间。3 ^3 3:由于三重循环结构紧凑
4 ^4 4:
Dijkstra算法的思想上是很容易接受的,但是实现上其实是非常麻烦的
21-3 Floyd算法 的 实现
- 第一步:存储图:使用的是领接矩阵

- 第二步:三重循环
设 m m m 为中介点、 i i i 为起点、 j j j 为终点,这一点很像 A*算法。
判断由 起点 i 起点i 起点i 直接到 终点 j 终点j 终点j 的代价值 是否大于 起点 i 起点i 起点i 经由 中介点 m 中介点m 中介点m 到 终点 j 终点j 终点j 的代价值(即判断 d p [ i ] [ j ] > d p [ i ] [ m ] + d p [ m ] [ j ] dp[i][j]>dp[i][m]+dp[m][j] dp[i][j]>dp[i][m]+dp[m][j]),若大于(判断成立)则将从 起点 i 起点i 起点i 直接到 终点 j 终点j 终点j 的代价值 更新为 d p [ i ] [ j ] = d p [ i ] [ m ] + d p [ m ] [ j ] dp[i][j]=dp[i][m]+dp[m][j] dp[i][j]=dp[i][m]+dp[m][j]
//法一:三目运算符直接搞定
dp[i][j] = dp[i][j] > (dp[i][m]+dp[m][j]) ? (dp[i][m]+dp[m][j]) : dp[i][j];
//法二:调用函数
dp[i][j] = min(dp[i][j], (dp[i][m]+dp[m][j]));
三重循环结束后,路径规划结束。

#include<bits/stdc++.h>
using namespace std;
const int INF=0x3f3f3f3f;
int dp[6][6]={{ 0, 2, 3, 6, INF, INF}, { 2, 0, INF, INF, 4, 6}, { 3, INF, 0, 2, INF, INF}, { 6, INF, 2, 0, 1, 3}, {INF, 4, INF, 1, 0, INF}, {INF, 6, INF, 3, INF, 0}
};
vector<vector<int>> Mid(6,vector<int>(6,INF));
char ch[6]={'A','B','C','D','E','F'};
void Floyd(int n){int m,i,j;for(m=0; m<n; m++) //k为中介点for(i=0; i<n;i++) //i为起点for(j=0; j<n;j++){ //j为终点if(dp[i][j] > (dp[i][m]+dp[m][j])){ //松弛操作dp[i][j] = (dp[i][m]+dp[m][j]);Mid[i][j]=m; //记录中介点}}
}
void Find_Path(int i, int j){if(Mid[i][j]==INF)cout<< ch[i];else{Find_Path(i, Mid[i][j]);i=Mid[i][j];while(Mid[i][j]!=INF){cout<< "->" << ch[ Mid[i][j] ] ;i=Mid[i][j];}}cout<< "->" << ch[j] <<endl;
}
int main(void){int n=6;Floyd(n);for(int i=0; i<n; i++){for(int j=0; j<n; j++){cout<< "结点" << ch[i] << "到结点" << ch[j] <<"的最短路径长为:" << dp[i][j] << ",";cout<<"最短路径为:";Find_Path(i,j);}cout<<endl;}return 0;
}
就纯一暴力法,没什么说的
相关文章:

【图论C++】Floyd算法(多源最短路径长 及 完整路径)
>>>竞赛算法 /*** file * author jUicE_g2R(qq:3406291309)————彬(bin-必应)* 一个某双流一大学通信与信息专业大二在读 * * brief 一直在算法竞赛学习的路上* * copyright 2023.9* COPYRIGHT 原创技术笔记ÿ…...
小谈设计模式(11)—模板方法模式
小谈设计模式(11)—模板方法模式 专栏介绍专栏地址专栏介绍 模板方法模式角色分类抽象类(Abstract Class)具体子类(Concrete Class)抽象方法(Abstract Method)具体方法(C…...
C#程序中很多ntdll.dll、clr.dll的线程
如下图 需要“右键工程——调试——取消勾选‘启用本地代码调试’”即可。...

低代码工作流程管理系统:提升企业运营效率的利器
业务运营状况是否良好,除了人员需要配合以外,真正发挥作用的是背后的工作流程。将重复的工作进行自动化处理,确保这些流程最终指向同一个目标、实现一致的运营结果。而设计和实施不佳的工作流程则产生相反的效果——导致处理时间延长、运营成…...

HIVE SQL regexp_extract和regexp_replace配合使用正则提取多个符合条件的值
《平凡的世界》评分不错,《巴黎圣母院》改变成的电影不错,还有<<1984>>也蛮好看。 如何使用regexp_extract®exp_replace函数将以上文本中所有书籍名称都提取出来? select substr(regexp_replace(regexp_extract(regexp_…...

debian 安装matlab2022b报错解决方法与问题解决思路
报错 terminate called after throwing an instance of ‘std::runtime_error’ 在安装目录执行 ./bin/glnxa64/MATLABWindow通过执行以上命令发现是和libharfbuzz库有关。 该库在调用freetype库时,有方法找不到。 偿试remove freetype库,发现该库有大…...

Jenkins集成AppScan实现
一、Jenkins上安装插件 在Jenkins里安装以下插件 ibm-security-appscanstandard-scanner 二、打开AppScan 1、配置需要扫描的地址 配置需要扫描的地址 2、记录好要扫描的URL登录序列 记录好要扫描的URL登录序列 3、导出要扫描的URL登录序列设置 导出要扫描的URL登录序列设置 三…...

10.1 File类
前言: java.io包中的File类是唯一一个可以代表磁盘文件的对象,它定义了一些用于操作文件的方法。通过调用File类提供的各种方法,可以创建、删除或者重命名文件,判断硬盘上某个文件是否存在,查询文件最后修改时间&…...

[论文笔记]UNILM
引言 今天带来论文Unified Language Model Pre-training for Natural Language Understanding and Generation的笔记,论文标题是 统一预训练语言模型用于自然语言理解和生成。 本篇工作提出了一个新的统一预训练语言模型(Unifield pre-trained Language Model,UniLM),可以同…...
LLM之Colossal-LLaMA-2:Colossal-LLaMA-2的简介、安装、使用方法之详细攻略
LLM之Colossal-LLaMA-2:Colossal-LLaMA-2的简介、安装、使用方法之详细攻略 导读:2023年9月25日,Colossal-AI团队推出了开源模型Colossal-LLaMA-2-7B-base。Colossal-LLaMA-2项目的技术细节,主要核心要点总结如下: >> 数据处…...
国庆作业2
select实现服务器并发 代码: #include <myhead.h>#define ERR_MSG(msg) do{\printf("%d\n",__LINE__);\perror(msg);\ }while(0)#define PORT 8888#define IP "192.168.1.5"int main(int argc, const char *argv[]) {//创建流式套接字…...

fork仓库的代码如何同步主仓库代码
1.背景 我fork了一份 jekyll-theme-chirpy 仓库的代码(基于 jekyll 的自建博客仓库,可以免服务器),我需要在上面更新我的博客文章,但是我又想一直同步 jekyll-theme-chirpy 仓库的新功能,这样我可以更新自己的博客功能。所以我就…...

【Axure】元件库和母版、常见的原型规范、静态原型页面制作
添加现有元件库 点击元件库——载入 当然也可以创建元件库,自己画自己保存 建立京东秒杀母版 静态原型页面的制作 框架 选择以iphone8的界面大小为例,顶部状态栏高度为20 左侧类似于标尺,因为图标、文字离最左侧的间距是不一样的 信…...

在设备树中描述中断
参考文档: 内核 Documentation\devicetree\bindings\interrupt-controller\interrupts.txt 在设备树中,中断控制器节点中必须有一个属性: interrupt-controller,表明它是“中断控制器”。 还必须有一个属性: #interru…...
ccf_csp第一题汇总
ccf_csp第一题汇总 printf()输出格式大全(附 - 示例代码)现值计算AcWing 4699. 如此编码AcWing 4509. 归一化处理(小数位数根号函数)AcWing 4454. 未初始化警告AcWing 4280. 序列查询AcWing 4006. 数组推导(小陷阱)AcWing 3292. 称检测点查询AcWing 3287…...
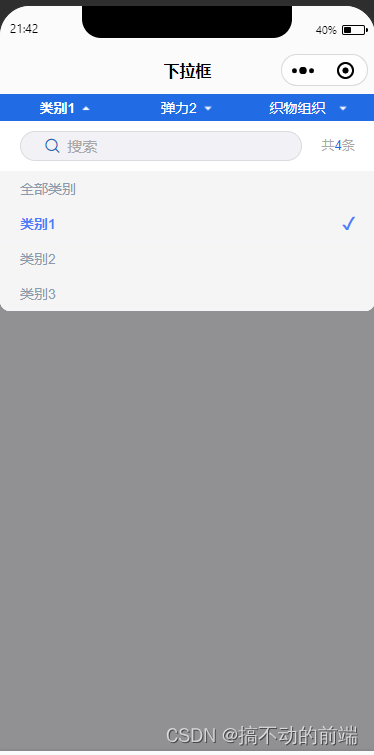
uniapp 实现下拉筛选框 二次开发定制
前言 最近又收到了一个需求,需要在uniapp 小程序上做一个下拉筛选框,然后找了一下插件市场,确实有找到,但不过他不支持搜索,于是乎,我就自动动手,进行了二开定制,站在巨人的肩膀上&…...
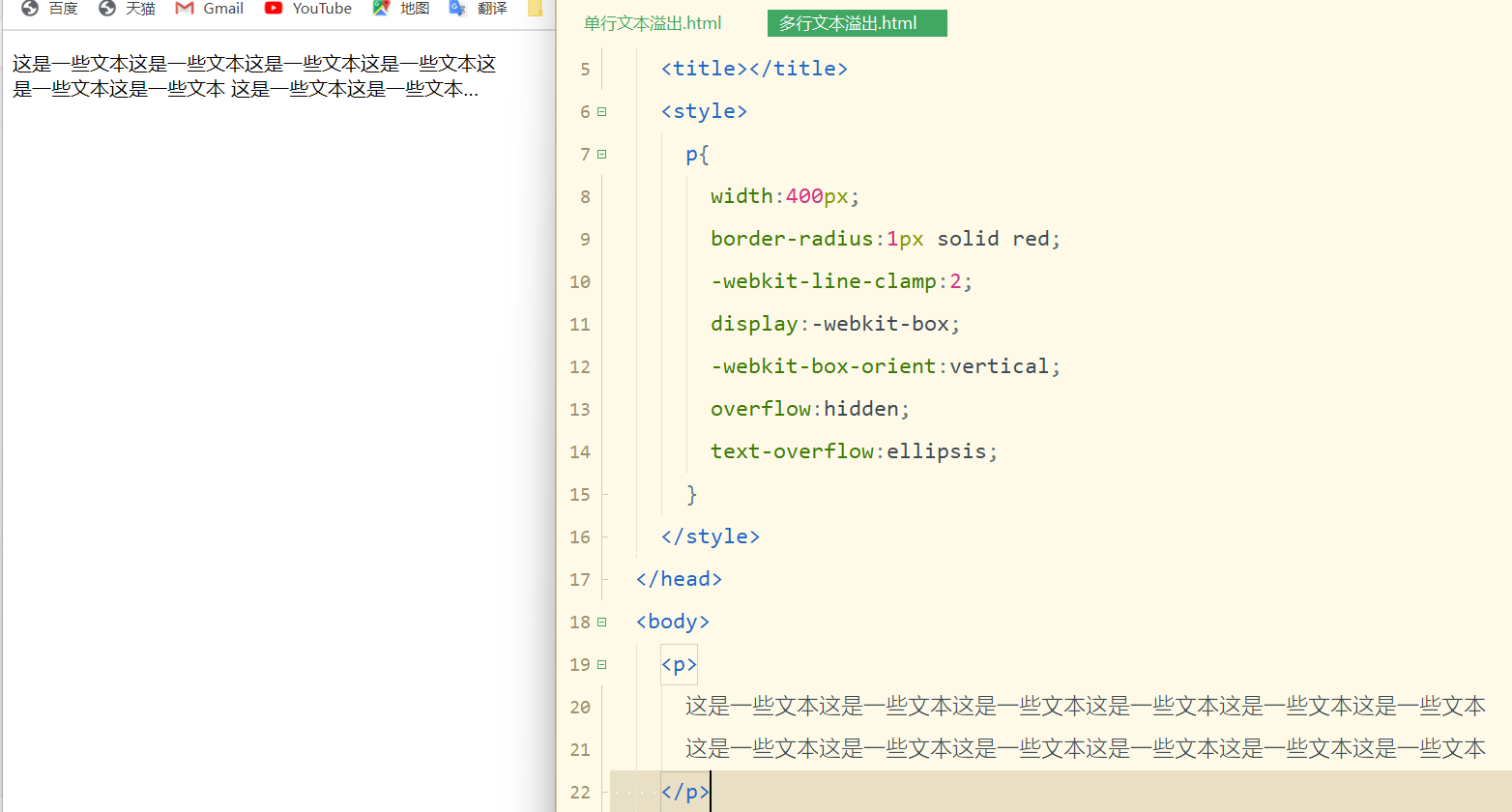
实现单行/多行文本溢出
在日常开发展示页面,如果一段文本的数量过长,受制于元素宽度的因素,有可能不能完全显示,为了提高用户的使用体验,这个时候就需要我们把溢出的文本显示成省略号。 一. 单行文本溢出 即文本在一行内显示,超出…...

Spring Boot中的Binder类
介绍 Spring Boot中的Binder类是一个用于绑定属性的工具类。它可以将配置文件中的属性值绑定到Java对象中,从而方便地进行配置管理。 简单示例 import org.springframework.boot.context.properties.bind.Binder; import org.springframework.core.env.Environmen…...

leetcode之打家劫舍
leetcode 198 打家劫舍 leetcode 213 打家劫舍 II leetcode 337. 打家劫舍 III 你是一个专业的小偷,计划偷窃沿街的房屋,每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈 ,这意味着第一个房屋和最后一个房屋是紧挨着的。同时&#…...

走进Spring的世界 —— Spring底层核心原理解析(一)
文章目录 前言一、Spring中是如何创建一个对象二、Bean的创建过程三、推断构造方法四、AOP大致流程五、Spring事务 前言 ClassPathXmlApplicationContext context new ClassPathXmlApplicationContext("config.xml"); UserService userService (UserService) cont…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...

MinIO Docker 部署:仅开放一个端口
MinIO Docker 部署:仅开放一个端口 在实际的服务器部署中,出于安全和管理的考虑,我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务,支持 Docker 部署,但默认情况下它需要两个端口:一个是 API 端口(用于存储和访问数据),另一个是控制台端口(用于管理界面…...

tomcat入门
1 tomcat 是什么 apache开发的web服务器可以为java web程序提供运行环境tomcat是一款高效,稳定,易于使用的web服务器tomcathttp服务器Servlet服务器 2 tomcat 目录介绍 -bin #存放tomcat的脚本 -conf #存放tomcat的配置文件 ---catalina.policy #to…...
