【剑指Offer】4.二维数组中的查找
题目
在一个二维数组array中(每个一维数组的长度相同),每一行都按照从左到右递增的顺序排序,每一列都按照从上到下递增的顺序排序。请完成一个函数,输入这样的一个二维数组和一个整数,判断数组中是否含有该整数。
[
[1,2,8,9],
[2,4,9,12],
[4,7,10,13],
[6,8,11,15]
]
给定 target = 7,返回 true。
给定 target = 3,返回 false。
数据范围:矩阵的长宽满足 0≤n,m≤500 , 矩阵中的值满足 0≤val≤10^9
进阶:空间复杂度 O(1) ,时间复杂度 O(n+m)
示例1
输入:7,[[1,2,8,9],[2,4,9,12],[4,7,10,13],[6,8,11,15]]
返回值:true
说明:存在7,返回true
示例2
输入:1,[[2]]
返回值:false
示例3
输入:3,[[1,2,8,9],[2,4,9,12],[4,7,10,13],[6,8,11,15]]
返回值:false
说明:不存在3,返回false
解答
源代码
import java.util.*;public class Solution {/*** 代码中的类名、方法名、参数名已经指定,请勿修改,直接返回方法规定的值即可** * @param target int整型 * @param array int整型二维数组 * @return bool布尔型*/public boolean Find (int target, int[][] array) {// write code herereturn mySolution(target, array, 0, array[0].length - 1);}public boolean mySolution (int target, int[][] array, int m, int n) {if (m >= array.length || n < 0) {return false;}if (array[m][n] == target) {return true;}if (array[m][n] > target) {n--;} else {m++;}return mySolution(target, array, m, n);}
}总结
这道题和LeetCode240相同。
题解详见【LeetCode】240.搜索二维矩阵Ⅱ
相关文章:

【剑指Offer】4.二维数组中的查找
题目 在一个二维数组array中(每个一维数组的长度相同),每一行都按照从左到右递增的顺序排序,每一列都按照从上到下递增的顺序排序。请完成一个函数,输入这样的一个二维数组和一个整数,判断数组中是否含有该…...

独立按键控制LED亮灭、独立按键控制LED状态、独立按键控制LED显示二进制、独立按键控制LED移位——“51单片机”
各位CSDN的uu们你们好呀,今天依旧是小雅兰的51单片机的内容,内容主要是:独立按键控制LED亮灭、独立按键控制LED状态、独立按键控制LED显示二进制、独立按键控制LED移位,下面,让我们进入51单片机的世界吧!&a…...
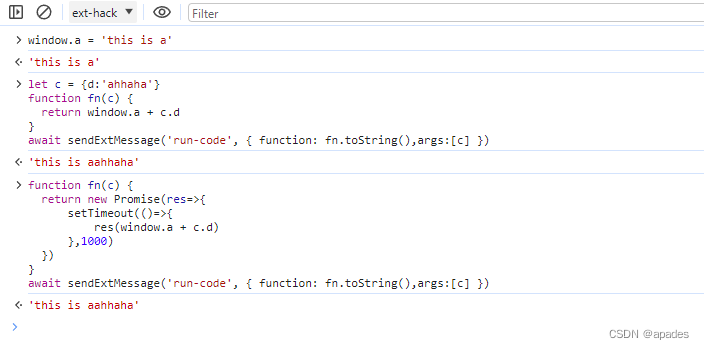
chrome extensions mv3通过content scripts注入/获取原网站的window数据
开发插件的都知道插件的content scripts和top window只共享Dom不共享window和其他数据,如果想拿挂载在window的数据还有点难度,下面会通过事件的方式传递cs和top window之间的数据写一个例子 代码 manifest.json 这里只搞了2个js,content.…...

震坤行API接口聚合解析,实现根据ID取商品详情
震坤行是一个工业品服务平台,提供了API接口供开发者使用。要根据ID获取商品详情,您需要使用震坤行API接口并进行相应的请求。 以下是使用震坤行API接口根据ID获取商品详情的示例代码(使用Python编写): import reques…...

mencpy和strcpy的区别?
今天刷题时遇到了这个问题,记录一下。 strcpy比较简单,就是拷贝字符串,遇到\0时结束拷贝。 memcpy用来做内存拷贝,可以拷贝任何数据类型的对象并指定拷贝数据的长度:char a[100],b[50]; memcpy(b, a, sizeof(b)); 总结…...
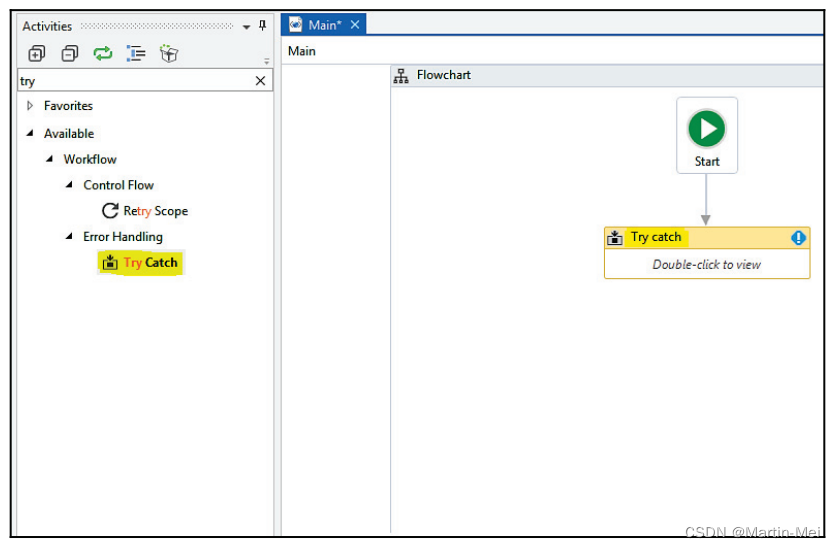
机器人过程自动化(RPA)入门 8. 异常处理、调试和日志记录
有时,自动化程序可能无法执行。为了处理此类情况,我们使用异常处理活动。在本章中,我们将从UiPath中可用的各种类型的异常处理方法、您可能遇到的异常以及如何处理它们开始。我们还将学习日志记录。本章涉及的一个重要主题是调试,以检查工作流是否正常工作,并更正任何错误…...

tomcat总结笔记
文章目录 Tomcat1、什么是tomcat?2、rpm安装jre环境3、源码安装jdk环境4、安装tomcat --源码安装5、相关目录文件webappsTomcat 配置文件目录介绍(conf)tomcat的相关管理命令在$prefix/bin目录下 实战1、:配置nginx动静分离实战2、配置基于t…...
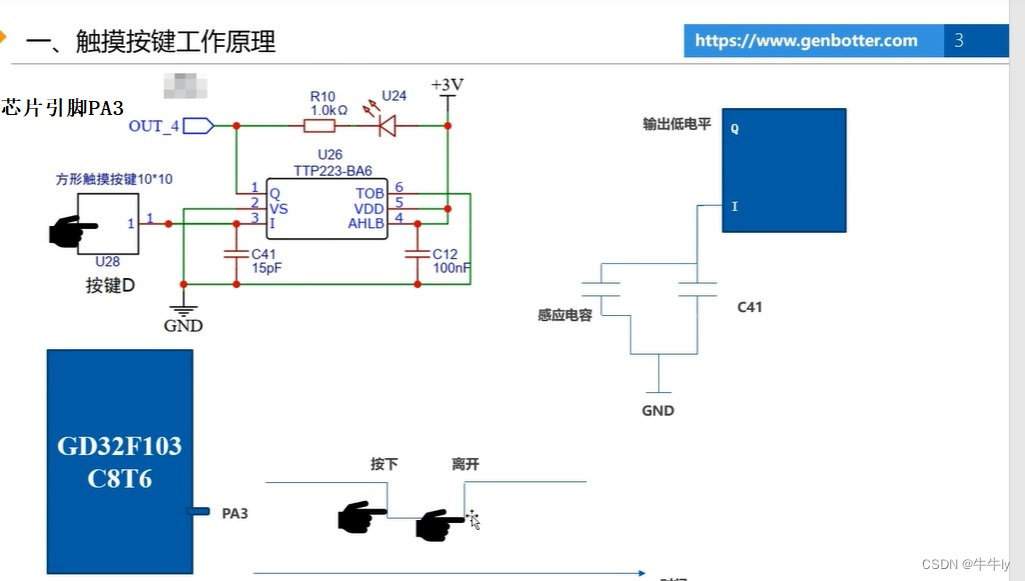
中断向量控制器(NVIC)
1. 什么是中断 在处理器中,中断是一个过程,即CPU在正常执行程序的过程中,遇到外部/内部的紧急事件需要处理,暂时中止当前程序的执行,转而去为处理紧急的事件,待处理完毕后再返回被打断的程序处继续往下执行…...
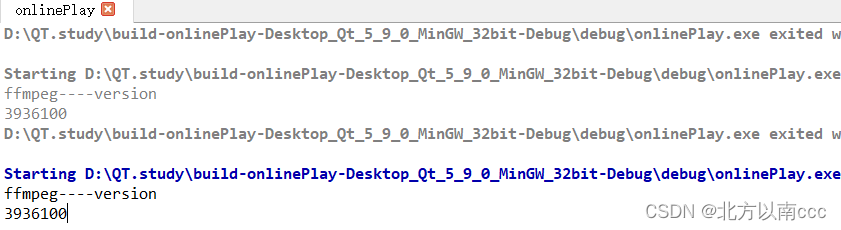
QT配置FFmpeg出现错误原因
文章目录 QT配置ffmpeg出现: undefined reference to "avcodec_version"没有配置环境变量QT和FFmpeg的版本不对应直接添加FFmpeg的头文件没有在.pro文件添加路径 QT 程序异常退出没有在debug文件里面存放dll库 QT配置ffmpeg出现: undefined re…...

列出使用Typescript的一些优点?
使用Typescript有以下优点: 类型安全:Typescript是一种静态类型语言,它要求在编码阶段明确定义变量和函数的类型。这种类型安全可以减少在运行时出现错误的可能性,并提高代码的可读性和可维护性。代码可读性和可维护性࿱…...
集成测试(Integration Testing, IT))
如何做好测试?(四)集成测试(Integration Testing, IT)
1. 集成测试的详细介绍: 集成测试(Integration Testing, IT),是一种软件测试方法,旨在验证不同组件、模块或子系统之间的交互和集成是否正常工作。它侧重于测试系统的组件之间的接口和数据传递,以确保它们…...
)
二叉树前序、中序、后序遍历(递归法、迭代法)
前序遍历:(练习题) 迭代法一: int TreeSize(struct TreeNode* root){return rootNULL?0:TreeSize(root->left)TreeSize(root->right)1; }int* preorderTraversal(struct TreeNode* root, int* returnSize){if(rootNULL){*…...

npm ,yarn 更换使用国内镜像源,淘宝源
背景 文章首发地址 在平时开发当中,我们经常会使用 Npm,yarn 来构建 web 项目。但是npm默认的源的服务器是在国外的,如果没有梯子的话。下载速度会特别慢。那有没有方法解决呢? 其实是有的,设置国内镜像即可&#x…...
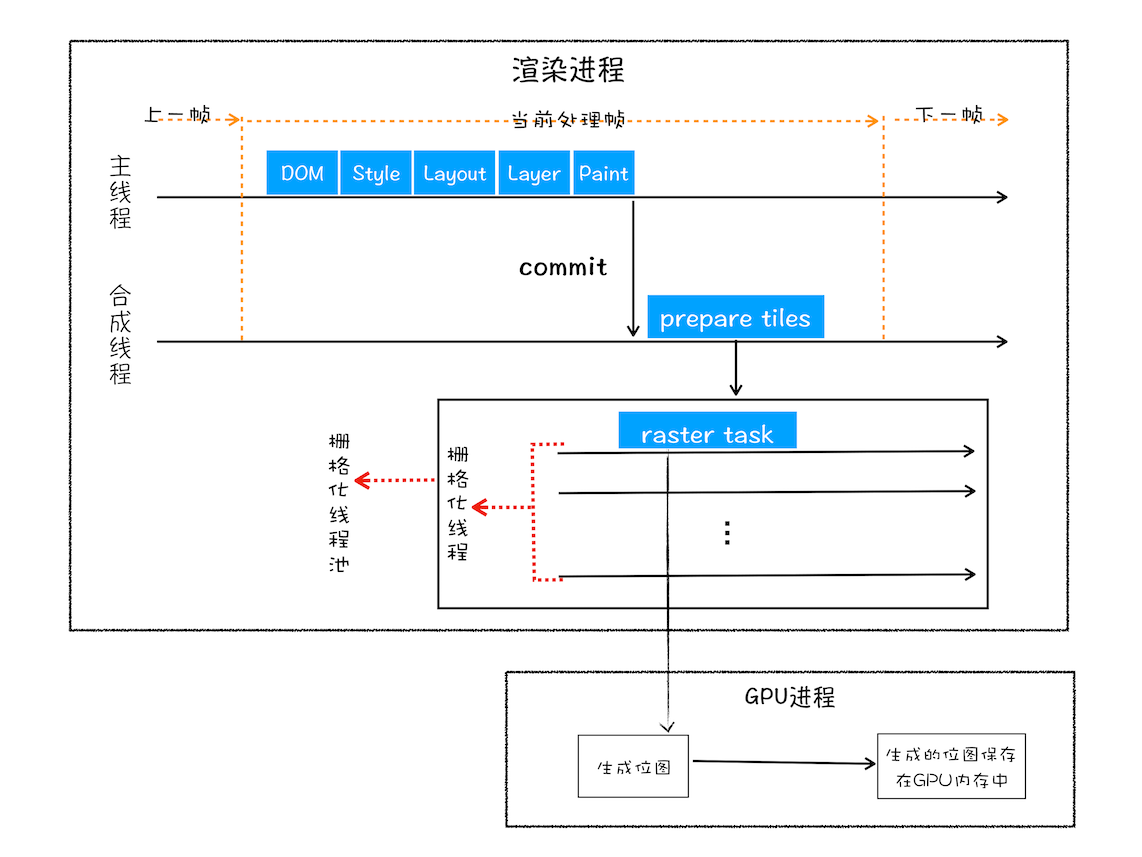
真正理解浏览器渲染更新流程
浏览器渲染更新过程 文章目录 浏览器渲染更新过程帧维度解释帧渲染过程一些名词解释Renderer进程GPU进程rendering(渲染) vs painting(绘制)⭐位图纹理Rasterize(光栅化) 1. 浏览器的某一帧开始:vsync2. Input event handlers3. requestAnimationFrame4. 强制重排(可…...

市场调研的步骤与技巧:助你了解市场需求
在当今快速发展的市场中,进行有效的市场研究对于了解消费者的行为、偏好和趋势至关重要。适当的市场研究可以帮助公司获得对目标受众的有价值的见解,创造更好的产品和服务,并提高客户满意度。今天,小编和大家一起讨论一下怎么做市…...

ansible的个人笔记使用记录-个人心得总结
1.shell模块使用,shell模块------执行命令,支持特殊符 ansible all -m shell -a yum -y install nginx ansible all -m shell -a systemctl restart nginx ansible all -m shell -a systemctl stop nginx && yum -y remove nginx2. file模块…...
相机数据恢复!详细步骤解析(2023新版)
和朋友在外面旅游用相机拍了好多有意义的照片和视频,但是导入电脑后不知道是被我删除了还是什么原因,这些照片都不见了,请问有方法恢复吗?” 在数字摄影时代,我们依赖相机记录珍贵的瞬间。然而,相机数据丢失…...

LNK2001: unresolved external symbol __imp___std_init_once_begin_initialize 问题解决
LNK2001: unresolved external symbol __imp___std_init_once_begin_initialize 解决 文章目录 问题背景方法一:使用预编译指令方法二:使用相同的环境 参考链接附录 问题背景 Visual Studio 2019 对 CMakeLists.txt 的支持不是很好,使用 “文…...
修改switch Nand无线区码 以支持高频5G 信道
环境:NS switch 问题:日版,港版无法连接大于44信道的5G WIFI 解决办法:修改PRODINFO.dec的WIFI 区域码 背景:我的switch是最早买的港版的一批,WIFI 只能连接日本的信道,家里的路由器是国行的&am…...
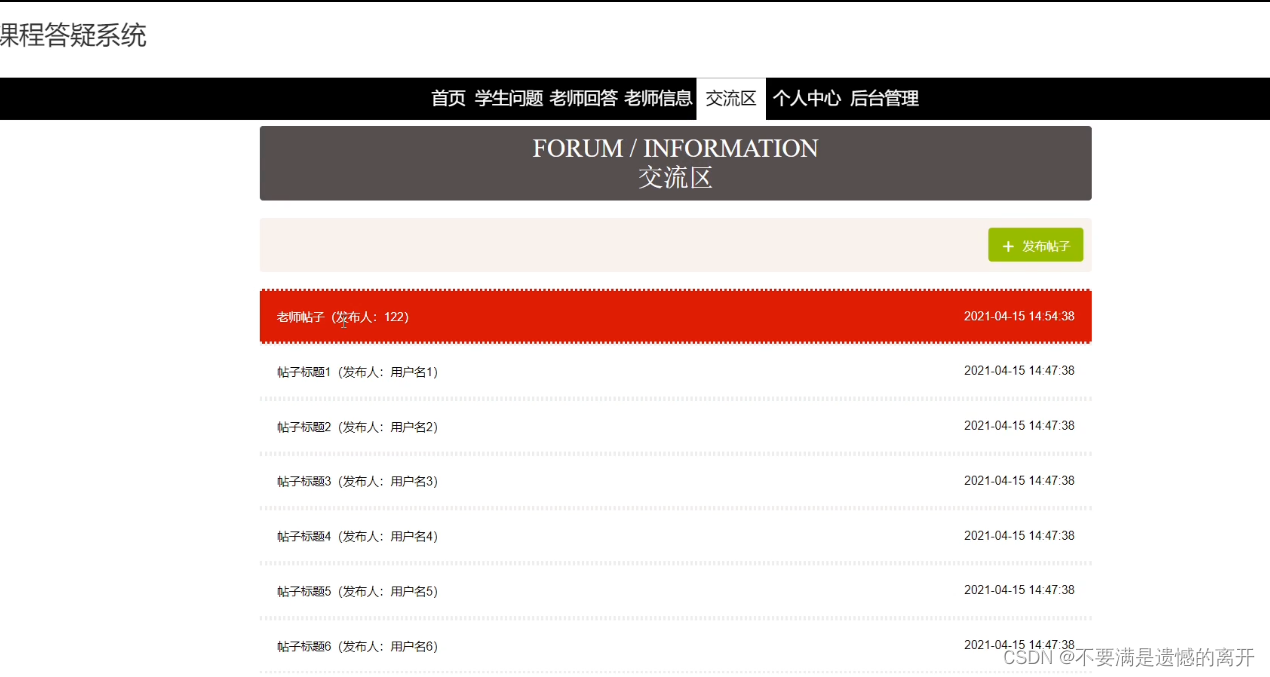
基于SpringBoot的课程答疑系统
目录 前言 一、技术栈 二、系统功能介绍 学生信息管理 科目类型管理 老师回答管理 我的收藏管理 学生问题 留言反馈 交流区 三、核心代码 1、登录模块 2、文件上传模块 3、代码封装 前言 随着信息互联网信息的飞速发展,无纸化作业变成了一种趋势&#x…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

初学 pytest 记录
安装 pip install pytest用例可以是函数也可以是类中的方法 def test_func():print()class TestAdd: # def __init__(self): 在 pytest 中不可以使用__init__方法 # self.cc 12345 pytest.mark.api def test_str(self):res add(1, 2)assert res 12def test_int(self):r…...

技术栈RabbitMq的介绍和使用
目录 1. 什么是消息队列?2. 消息队列的优点3. RabbitMQ 消息队列概述4. RabbitMQ 安装5. Exchange 四种类型5.1 direct 精准匹配5.2 fanout 广播5.3 topic 正则匹配 6. RabbitMQ 队列模式6.1 简单队列模式6.2 工作队列模式6.3 发布/订阅模式6.4 路由模式6.5 主题模式…...
