Shapiro-Wilk正态性检验(Shapiro和Wilk于1965年提出)
Shapiro-Wilk正态性检验是一种用于确定数据集是否服从正态分布的统计方法。它基于Shapiro和Wilk于1965年提出的检验统计量。以下是其基本原理和用途:
基本原理:
-
零假设(Null Hypothesis):Shapiro-Wilk检验的零假设是数据集来自于正态分布。这意味着,如果数据确实服从正态分布,则零假设成立。
-
计算Shapiro-Wilk统计量:检验首先计算Shapiro-Wilk统计量,这是一个衡量数据与正态分布拟合的度量。该统计量基于数据的观察值和正态分布的期望值之间的差异。
-
与临界值比较:接下来,Shapiro-Wilk统计量与临界值进行比较。临界值是根据所选的显著性水平(通常为5%)和数据集的大小计算得出的。如果Shapiro-Wilk统计量小于临界值,就意味着数据不太可能来自于正态分布。
-
做出决策:根据统计量与临界值的比较,可以决定是否拒绝零假设。如果统计量足够小,小于临界值,通常会拒绝零假设,这意味着数据不服从正态分布。否则,不能拒绝零假设,这表示数据可能服从正态分布。
用途:
-
数据分布检查:Shapiro-Wilk检验可用于验证数据是否符合正态分布的假设。这对于许多统计分析和模型建立的前提非常重要,因为许多统计方法都要求数据服从正态分布。
-
质量控制:在制造业和质量控制中,Shapiro-Wilk检验可以用来检查生产过程是否产生了正态分布的输出。如果不是,可能需要采取措施来改进过程。
-
金融分析:在金融领域,正态分布假设经常用于分析资产价格变动。Shapiro-Wilk检验可以用来验证这种假设的有效性。
-
生物统计学:在生物统计学中,研究人员可能使用Shapiro-Wilk检验来确定生物数据是否遵循正态分布,例如基因表达数据或生物测量数据。
总之,Shapiro-Wilk正态性检验是一种常用的统计工具,可用于验证数据是否符合正态分布的假设,从而支持各种领域的分析和决策。它在小样本情况下的效力较高,适用于许多统计问题。
from scipy import stats
import numpy as np# 创建一个示例数据集(这里使用正态分布数据)
data = np.random.normal(0, 1, 100)# 执行Shapiro-Wilk正态性检验
statistic, p_value = stats.shapiro(data)# 输出检验结果
print("Shapiro-Wilk统计量:", statistic)
print("p-value:", p_value)# 根据p-value做出决策
alpha = 0.05 # 显著性水平
if p_value > alpha:print("不能拒绝零假设,数据可能服从正态分布")
else:print("拒绝零假设,数据不服从正态分布")
Shapiro-Wilk正态性检验对检验样本大小有一定的要求。具体来说,Shapiro-Wilk检验在样本大小较小(通常小于大约50-200,具体取决于不同文献和实践)时可能不太适用,并且在这种情况下其效力可能会降低。这是由于统计检验的性质和假设。
主要的考虑因素包括:
-
统计性能:Shapiro-Wilk检验在大样本下通常具有较好的统计性能,可以较好地检测到数据的偏离正态分布的情况。但是在小样本下,其性能可能较差,可能无法可靠地识别非正态性。
-
假设的严格性:Shapiro-Wilk检验对于样本大小的要求与其检验假设的严格性有关。较小的样本容易受到偶然因素的影响,从而影响检验的结果。
-
显著性水平:样本大小较小时,为了达到一定的显著性水平,需要更大的统计效力。这可能需要更严格的判定标准,从而增加了拒绝零假设的难度。
如果你的样本较小,而且需要进行正态性检验,可以考虑使用其他方法,如观察Q-Q图、直方图、小样本正态性检验(如Shapiro-Francia检验),或者考虑非参数统计方法,这些方法在小样本情况下可能更适合。此外,正态性检验通常应与领域知识和问题的背景结合使用,而不应仅仅依赖于统计检验的结果。
相关文章:
)
Shapiro-Wilk正态性检验(Shapiro和Wilk于1965年提出)
Shapiro-Wilk正态性检验是一种用于确定数据集是否服从正态分布的统计方法。它基于Shapiro和Wilk于1965年提出的检验统计量。以下是其基本原理和用途: 基本原理: 零假设(Null Hypothesis):Shapiro-Wilk检验的零假设是数…...
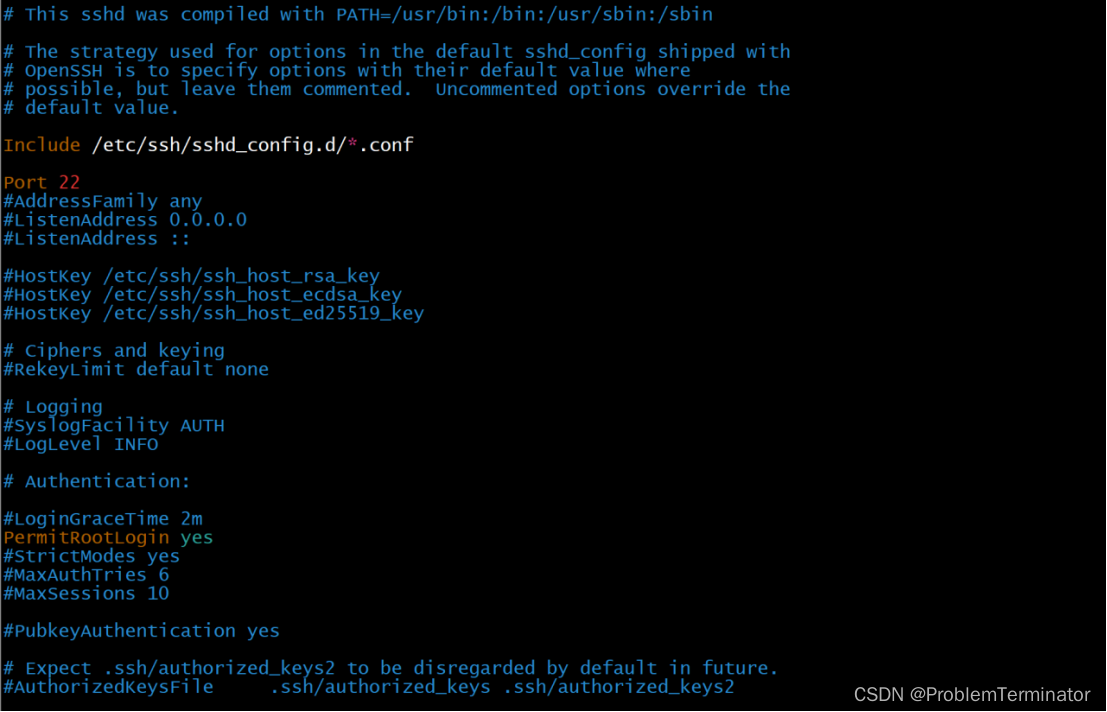
debian设置允许ssh连接
解决新debian系统安装后不能通过ssh连接的问题。 默认情况下,Debian系统不开启SSH远程登录,需要手动安装SSH软件包并设置开机启动。 > 设置允许root登录传送门:debian设置允许root登录 首先检查/etc/ssh/sshd_config文件是否存在。 注意…...

【C语言经典100例题-66】(用指针解决)输入3个数a,b,c,按大小顺序输出。
代码: #include<stdio.h> #define _CRT_SECURE_NO_WARNINGS 1//VS编译器使用scanf函数时会报错,所以添加宏定义 swap(p1, p2) int* p1, * p2; {int p;p *p1;*p1 *p2;*p2 p; } int main() {int n1, n2, n3;int* pointer1, * pointer2, * point…...

【STM32 CubeMX】移植u8g2(一次成功)
文章目录 前言一、下载u8g2源文件二、复制和更改文件2.1 复制文件2.2 修改文件u8g2_d_setup文件u8g2_d_memory 三、编写oled.c和oled.h文件3.1 CubeMX配置I2C3.2 编写文件oled.holed.c 四、测试代码main函数测试代码 总结 前言 在本文中,我们将介绍如何在STM32上成…...

华为云智能化组装式交付方案 ——金融级PaaS业务洞察及Web3实践的卓越贡献
伴随信息技术与金融业务加速的融合,企业应用服务平台(PaaS)已从幕后走向台前,成为推动行业数字化转型的关键力量。此背景下,华为云PaaS智能化组装式交付方案闪耀全场,在近日结束的华为全联接大会 2023上倍受…...
)
Halcon Image相关算子(二)
(1) dyn_threshold(OrigImage, ThresholdImage : RegionDynThresh : Offset, LightDark : ) 功能:从输入图像中选择像素满足阈值条件的那些区域。 图形输入参数:OrigImage:原始图像; 图形输入参数:ThresholdImage&a…...

Rust 多线程编程
一个进程一定有一个主线程,主线程之外创建出来的线程称为子线程 多线程编程,其实就是在主线程之外创建子线程,让子线程和主线程并发运行,完成各自的任务。 Rust语言支持多线程编程。 Rust语言标准库中的 std::thread 模块用于多线…...

JavaScript高阶班之ES6 → ES11(八)
JavaScript高阶班之ES6 → ES11 1、ES6新特性1.1、let 关键字1.2、const关键字1.3、变量的解构赋值1.3.1、数组的解构赋值1.3.2、对象的解构赋值 1.4、模板字符串1.5、简化对象写法1.6、箭头函数1.7、函数参数默认值1.8、rest参数1.9、spread扩展运算符1.9.1、数组合并1.9.2、数…...

网页中嵌套网页制作方法
<!DOCTYPE html> <html> <head> <meta name"viewport" content"widthdevice-width, initial-scale1.0"> <meta charset"UTF-8"> <title>网页搜索</title> <style> body { ba…...
)
系统集成项目管理总结(笔记)
系统集成项目管理总结 基础知识 第一章 信息化知识 第二章 信息系统服务管理 第三章 系统集成专业技术 第四章 项目管理一般知识 第五章 立项管理 第六章 整体管理 第七章 范围管理 第八章 进度管理 第九章 成本管理 第十章 质量管理 第十一章 人力资源管理 第十二…...

如何给Nginx配置访问IP白名单
一、Nginx配置访问IP白名单 有时部署的应用需要只允许某些特定的IP能够访问,其他IP不允许访问,这时,就要设置访问白名单; 设置访问白名单有多种方式: 1.通过网络防火墙配置,例如阿里云/华为云管理平台 2.…...

【VIM】VIM配合使用的工具
6-1 课程总结-vim虐我千百遍,我待 vim 如初恋_哔哩哔哩_bilibili...
git你学“废”了吗?——git本地仓库的创建
git你学“废”了吗?——git本地仓库的创建😎 前言🙌初识gitgit 本地仓库的创建1、基于centos7环境下 git的下载2、设置自己的用户名和邮箱 查看.git中的结构区分清楚版本库和工作区 查看git中的相关内容查看仓库的状态 总结撒花💞…...
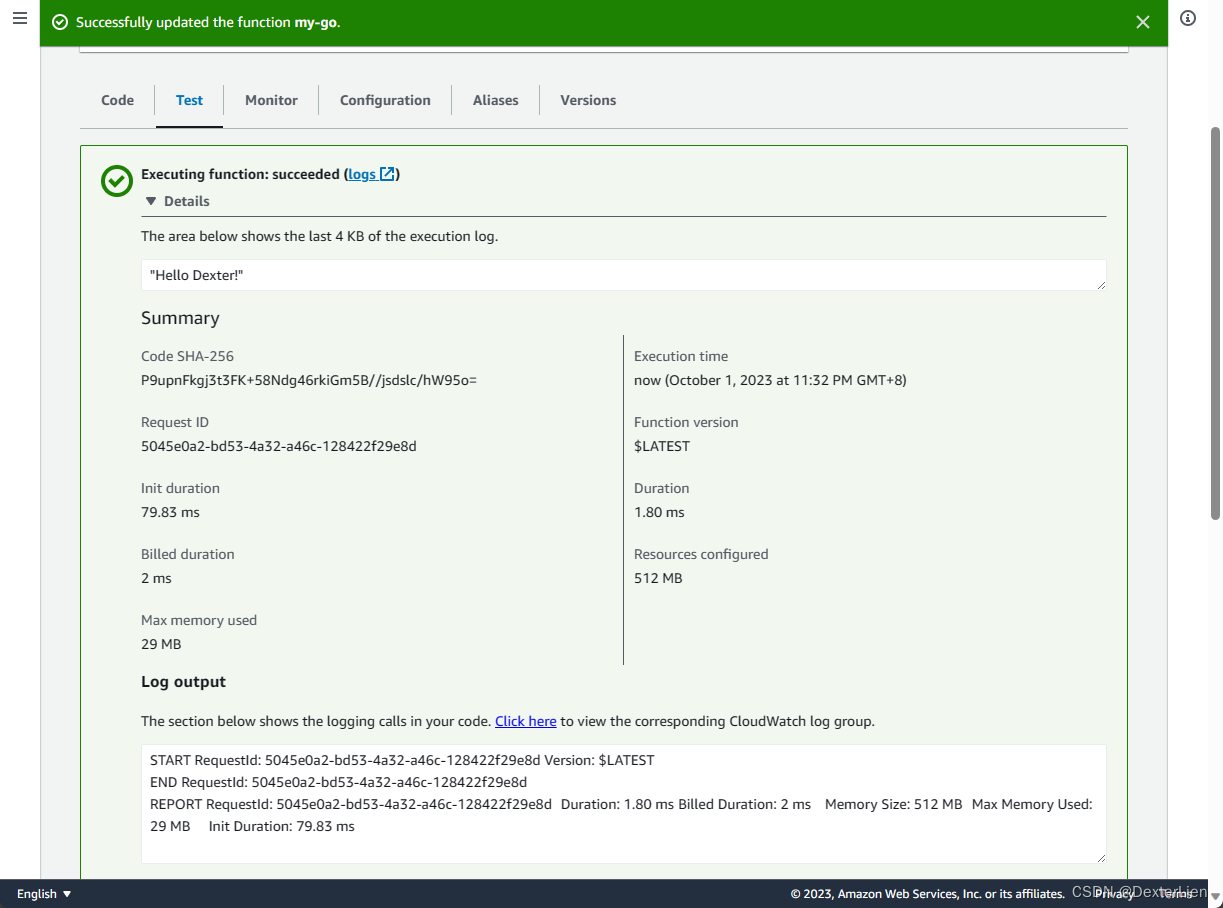
AWS Lambda Golang HelloWorld 快速入门
操作步骤 以下测试基于 WSL2 Ubuntu 22.04 环境 # 下载最新 golang wget https://golang.google.cn/dl/go1.21.1.linux-amd64.tar.gz# 解压 tar -C ~/.local/ -xzf go1.21.1.linux-amd64.tar.gz# 配置环境变量 PATH echo export PATH$PATH:~/.local/go/bin >> ~/.bashrc …...

【C++】单例模式
文章目录 一. 介绍二. 饿汉模式三. 懒汉模式四. 饿汉模式和懒汉模式对比 一. 介绍 单例模式是属于设计模式的一种,那什么是设计模式呢? 设计模式(Design Pattern)是一套被反复使用、多数人知晓的、经过分类的、代码设计经验的总…...

【kubernetes】使用luakube访问kubernetes api
文章目录 1 kubernetes client2 luakube初体验3 luakube代码分析4 luakube包的调用5 lua相关5.1 self5.2 metatable5.2.1 使用metatable对table新增操作符5.2.2 使用metatable对table新增方法5.2.3 再探luakube 6 参考文档 1 kubernetes client 客户端列出了各种语言对应的访问…...
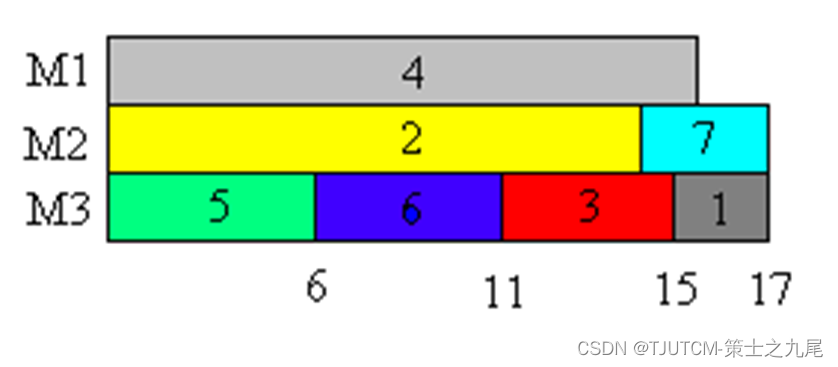
【算法分析与设计】贪心算法(下)
目录 一、单源最短路径1.1 算法基本思想1.2 算法设计思想1.3 算法的正确性和计算复杂性1.4 归纳证明思路1.5 归纳步骤证明 二、最小生成树2.1 最小生成树性质2.1.1 生成树的性质2.1.2 生成树性质的应用 2.2 Prim算法2.2.1 正确性证明2.2.2 归纳基础2.2.3 归纳步骤2.3 Kruskal算…...
Arm Cache学习资料大汇总
关键词:cache学习、mmu学习、cache资料、mmu资料、arm资料、armv8资料、armv9资料、 trustzone视频、tee视频、ATF视频、secureboot视频、安全启动视频、selinux视频,cache视频、mmu视频,armv8视频、armv9视频、FF-A视频、密码学视频、RME/CC…...
—— Dockerfile 编写技巧总结)
Docker 学习总结(79)—— Dockerfile 编写技巧总结
目标 更快的构建速度 更小的 Docker 镜像大小 更少的 Docker 镜像层 充分利用镜像缓存 增加 Dockerfile 可读性 让 Docker 容器使用起来更简单 总结 编写 .dockerignore 文件 容器只运行单个应用 将多个 RUN 指令合并为一个 基础镜像的标签不要用 latest 每个 RUN 指令后删除多…...

链表经典面试题(二)
返回中间结点 1.中间结点的题目2.中间结点的图文分析3.中间结点的基本代码4.中间结点的优化代码 1.中间结点的题目 2.中间结点的图文分析 方法1:先求整体长度,再除以2,所得到的就是中间结点 方法2:双指针法,快指针走两…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

Redis:现代应用开发的高效内存数据存储利器
一、Redis的起源与发展 Redis最初由意大利程序员Salvatore Sanfilippo在2009年开发,其初衷是为了满足他自己的一个项目需求,即需要一个高性能的键值存储系统来解决传统数据库在高并发场景下的性能瓶颈。随着项目的开源,Redis凭借其简单易用、…...

2025年- H71-Lc179--39.组合总和(回溯,组合)--Java版
1.题目描述 2.思路 当前的元素可以重复使用。 (1)确定回溯算法函数的参数和返回值(一般是void类型) (2)因为是用递归实现的,所以我们要确定终止条件 (3)单层搜索逻辑 二…...
