Leetcode 69.x的平方根

给你一个非负整数 x ,计算并返回 x 的 算术平方根 。
由于返回类型是整数,结果只保留 整数部分 ,小数部分将被 舍去 。
注意:不允许使用任何内置指数函数和算符,例如 pow(x, 0.5) 或者 x ** 0.5 。
示例 1:
输入:x = 4 输出:2
示例 2:
输入:x = 8 输出:2 解释:8 的算术平方根是 2.82842..., 由于返回类型是整数,小数部分将被舍去。
提示:
0 <= x <= 231 - 1
一、信息
1.给我的是非负整数x
2.计算x的算术平方根
3.返回类型是整型
二、分析
条件1:告诉我不用考虑输入为负数
条件2:告诉我两点。第一点就是告诉我是算术平方根如果只是普通的平方根输出的时候还要输出正负两个答案。第二点就是告诉我此次的目的。
条件3 告诉我函数的返回值类型。
三、算法步骤:
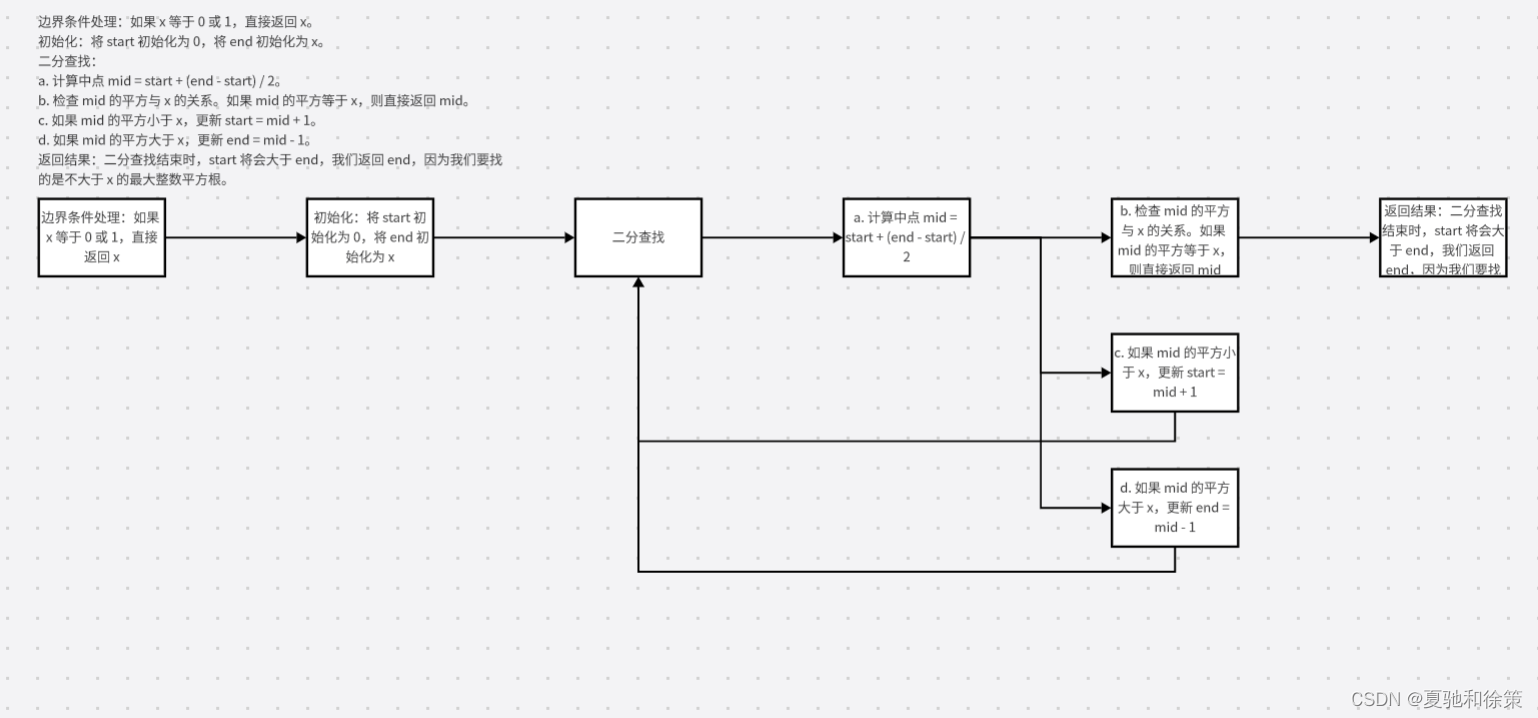
流程图:
四、问题出现
问题1.该如何实现开方呢?
我的思路:
我看到了在我面前有两条路。
第一条:遍历
我们设x为目标y为被开方的数,我们假设存在0<x<y使得x*x=y,我们只需要再y中一遍一遍试就行。这样的话时间复杂度应该为O(n).
第二条:遍历后用二分法提高查找效率。
更正后的思考过程
一、信息
我们要实现一个函数,这个函数接收一个非负整数 `x` ,计算并返回 `x` 的算术平方根的整数部分。我们不能使用内置的指数函数和算符,例如 `pow(x, 0.5)` 或者 `x ** 0.5`。
二、分析
初始思考:
一开始,我思考的是如何在没有使用平方根函数的情况下得到一个数的平方根。考虑到平方根的定义是,对于一个非负数 `x` ,其平方根是另一个非负数,这个数的平方等于 `x`。于是我们需要找到一个数,使其平方最接近且不大于 `x`。
#### 遇到的问题:
1. 我们不能直接计算平方根,所以我们需要使用一些间接的方法来找到这个数。
2. 我们需要考虑效率问题。例如,我们可以从 `0` 开始,一点一点地增加,直到我们找到这个数。但是这种方法效率很低,特别是当 `x` 很大时。
#### 解决方案:
考虑到效率问题,我们可以使用二分查找法。我们知道,对于一个非负整数 `x` ,其平方根不会大于 `x/2 + 1`。所以我们可以在 `0` 到 `x/2 + 1` 之间进行二分查找。这将大大减少我们需要检查的数字的数量,从而提高效率。
三、算法步骤
1. **边界条件处理**:如果 `x` 等于 `0` 或 `1`,直接返回 `x`。
2. **初始化**:将 `start` 初始化为 `0`,将 `end` 初始化为 `x`。
3. **二分查找**:
a. 计算中点 `mid = start + (end - start) / 2`。
b. 检查 `mid` 的平方与 `x` 的关系。如果 `mid` 的平方等于 `x`,则直接返回 `mid`。
c. 如果 `mid` 的平方小于 `x`,更新 `start = mid + 1`。
d. 如果 `mid` 的平方大于 `x`,更新 `end = mid - 1`。
4. **返回结果**:二分查找结束时,`start` 将会大于 `end`,我们返回 `end`,因为我们要找的是不大于 `x` 的最大整数平方根。
通过这个方法,我们可以高效地找到一个数的平方根的整数部分,而无需使用任何内置的平方根函数或算符。
五、实现
我的答案:
C语言版本:
#include <stdio.h>int mySqrt(int x) {if (x == 0 || x == 1) return x;long long start = 0;long long end = x;while (start <= end) {long long mid = start + (end - start) / 2;if (mid * mid == x) return mid; // 找到了精确的平方根if (mid * mid < x) {start = mid + 1;} else {end = mid - 1;}}// 由于题目要求返回整数部分,所以返回endreturn end;
}int main() {int x1 = 4;int x2 = 8;printf("The square root of %d is %d\n", x1, mySqrt(x1)); // 输出:2printf("The square root of %d is %d\n", x2, mySqrt(x2)); // 输出:2return 0;
}
C++版本:
#include <iostream>class Solution {
public:int mySqrt(int x) {if (x == 0 || x == 1) return x;long long start = 0, end = x;while (start <= end) {long long mid = start + (end - start) / 2;if (mid * mid == x) return mid; // 找到了精确的平方根if (mid * mid < x) start = mid + 1;else end = mid - 1;}// 返回end,因为我们要返回的是不大于x的最大整数平方根return end;}
};int main() {Solution solution;std::cout << "The square root of 4 is " << solution.mySqrt(4) << std::endl; // 输出:2std::cout << "The square root of 8 is " << solution.mySqrt(8) << std::endl; // 输出:2return 0;
}
JAVA:
public class Solution {public int mySqrt(int x) {if (x == 0 || x == 1) return x;long start = 0, end = x;while (start <= end) {long mid = start + (end - start) / 2;if (mid * mid == x) return (int) mid; // 找到了精确的平方根if (mid * mid < x) start = mid + 1;else end = mid - 1;}// 返回end,因为我们要返回的是不大于x的最大整数平方根return (int) end;}public static void main(String[] args) {Solution solution = new Solution();System.out.println("The square root of 4 is " + solution.mySqrt(4)); // 输出:2System.out.println("The square root of 8 is " + solution.mySqrt(8)); // 输出:2}
}
Leetcode 题解:
方法三:牛顿迭代

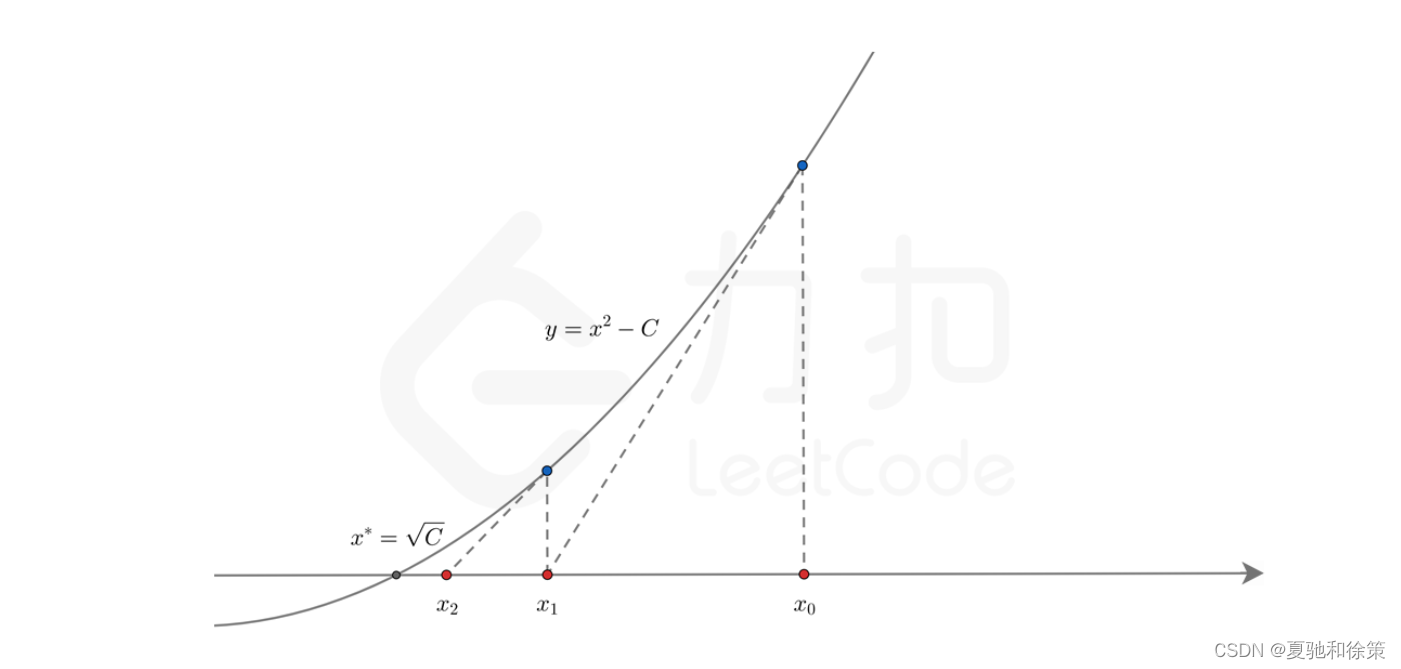


源代码:
class Solution {
public:int mySqrt(int x) {if (x == 0) {return 0;}double C = x, x0 = x;while (true) {double xi = 0.5 * (x0 + C / x0);if (fabs(x0 - xi) < 1e-7) {break;}x0 = xi;}return int(x0);}
};我的答案和Leetcode的答案的各自的优劣
二分查找法和牛顿迭代法都是有效的数值方法,用于求解平方根,它们各自有一些优劣势:
### 1. **二分查找法**:
#### 优势:
- **直观易懂**:二分查找法是一种非常直观且易于理解和实现的算法。
- **稳定性高**:由于算法逻辑简单,因此其在各种情况下都表现得很稳定。
- **适用性广**:二分查找法可以应用于任何有序序列,不仅仅局限于求平方根。
#### 劣势:
- **收敛速度**:相较于牛顿迭代法,二分查找法的收敛速度较慢,尤其是在求解较大的数的平方根时。
### 2. **牛顿迭代法**:
#### 优势:
- **收敛速度快**:牛顿迭代法是一种二次收敛的方法,每一次迭代都会使得结果的有效数字大约翻倍,因此通常会比二分查找法更快地收敛到实际的平方根。
- **适用性强**:牛顿迭代法可以用来求解各种非线性方程的根,适用性非常广泛。
#### 劣势:
- **实现复杂度**:相较于二分查找法,牛顿迭代法的实现略显复杂。
- **初始值选择**:牛顿迭代法的收敛性会受到初始值选择的影响,而选择合适的初始值有时并非易事。
### 综合比较:
对于求平方根这一特定问题而言,如果追求算法的简单和稳定,二分查找是一个很好的选择。而如果追求更高的收敛速度,尤其是在处理较大的数时,牛顿迭代法会是更优的选择。在实际应用中,可以根据问题的具体要求和约束来选择最合适的方法。
总结:
从这道题目中,我们能学到多方面的知识和技能:
### 1. **算法基础**
- **二分查找**:学会使用二分查找来求解有序序列中的问题,理解其工作原理和实现方法。
- **牛顿迭代**:学会使用牛顿迭代法来快速求解非线性方程的根,理解其收敛性和收敛速度。
### 2. **编程实践**
- **实现方法**:学会如何将算法用代码实现,例如C++或Java中如何实现二分查找和牛顿迭代法。
- **调试和优化**:通过实践,学会如何调试代码,优化算法性能,如何选择合适的初始值和终止条件等。
### 3. **数学知识**
- **函数和图像理解**:通过牛顿迭代法,加深对函数、导数和图像的理解,学习如何通过图像直观理解算法过程。
- **收敛性理解**:通过对比不同方法,理解算法的收敛性和收敛速度,学会如何评估算法的性能。
### 4. **问题解决技能**
- **多种解决方案**:学会对同一问题采用不同的解决方案,并能够分析各种方案的优劣,从而选择最合适的一种。
- **分析和评估**:学会分析问题的需求和限制,评估不同方案的适用性,做出合理的决策。
### 5. **实际应用**
- **实际问题中的应用**:学会如何将学到的算法和知识应用到实际问题中,例如在没有开方运算的环境中求解平方根。
- **性能优化**:了解在实际应用中如何优化算法,提高算法的运行效率,满足实际需求。
总之,这道题目不仅可以加深对基础算法和编程的理解,而且可以提高数学理论和问题解决能力,具有很高的学习价值。

相关文章:

Leetcode 69.x的平方根
给你一个非负整数 x ,计算并返回 x 的 算术平方根 。 由于返回类型是整数,结果只保留 整数部分 ,小数部分将被 舍去 。 注意:不允许使用任何内置指数函数和算符,例如 pow(x, 0.5) 或者 x ** 0.5 。 示例 1࿱…...

Node18.x基础使用总结(二)
Node18.x基础使用总结 1、Node.js模块化1.1、模块暴露数据1.2、引入模块 2、包管理工具2.1、npm2.2、npm的安装2.3、npm基本使用2.4、搜索包2.5、下载安装包2.6、生产环境与开发环境2.7、生产依赖与开发依赖2.8、全局安装2.9、修改windows执行策略2.10、安装包依赖2.11、安装指…...

LCD 的RGB接口(SYNC Mode/ SYNC-DE Mode/ DE Mode)
1、 SYNC Mode Timing Diagram 2、 SYNC-DE Mode Timing Diagram 3、 DE Mode Timing Diagram RGB接口(SYNC Mode/ SYNC-DE Mode/ DE Mode)-CSDN博客...

flink生成水位线记录方式--周期性水位线生成器
背景 在flink基于事件的时间处理中,水位线记录的生成是一个很重要的环节,本文就来记录下几种水位线记录的生成方式的其中一种:周期性水位线生成器 周期性水位线生成器 1.1 BoundedOutOfOrdernessTimeStampExtractor 他会接收一个表示最大延…...
百度资源搜索平台出现:You do not have the proper credential to access this page.怎么办?
Forbidden site not allowed You do not have the proper credential to access this page. If you think this is a server error, please contact the webmaster. 如果你的百度资源平台,点进去出现这个提示,说明您的网站已经被百度清退了。如果你的网站…...
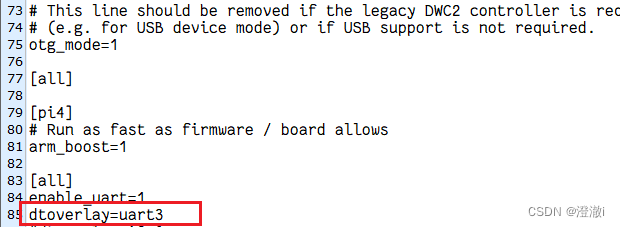
树莓派CM4开启I2C与UART串口登录同时serial0映射到ttyS0 开启多串口
文章目录 前言1. 树莓派开启I2C与UART串口登录2. 开启多串口总结: 前言 最近用CM4的时候使用到了I2C以及多个UART的情况。 同时配置端口映射也存在部分问题。 这里集中记录一下。 1. 树莓派开启I2C与UART串口登录 输入指令sudo raspi-config 跳转到如下界面&#…...

【租车骑绿道】python实现-附ChatGPT解析
1.题目 租车骑绿道 时间限制:1s 空间限制:256MB 限定语言:不限 题目描述: 部门组织绿道骑行团建活动。租用公共双人自行车骑行,每辆自行车最多坐两人、做大载重M。 给出部门每个人的体重,请问最多需要租用多少双人自行车 输入描述 第一行两个数字m、n,自行车限重m,代表部门总…...
【ONE·Linux || 多线程(一)】
总言 多线程:进程线程基本概念、线程控制、互斥与同步。 文章目录 总言1、基本概念1.1、补充知识1.1.1、堆区细粒度划分1.1.2、虚拟地址到物理空间的转化 1.2、如何理解线程、进程1.2.1、如何理解线程?1.2.2、如何理解进程? 1.3、实践操作1.…...

华为智能企业上网行为管理安全解决方案(1)
华为智能企业上网行为管理安全解决方案(1) 课程地址方案背景需求分析企业上网行为概述企业上网行为安全风险分析企业上网行为管理需求分析 方案设计组网架构设备选型设备简介行为管理要点分析方案功能概述 课程地址 本方案相关课程资源已在华为O3社区发…...

Acwing 240. 食物链
Acwing 240. 食物链 题目描述思路讲解代码展示 题目描述 思路讲解 代码展示 #include <iostream>using namespace std;const int N 50010;int n, m; int p[N], d[N]; //p[]是并查集的father,d[]是距离int find(int x) {if (p[x] ! x) { //如果说x不是树根的话int t f…...

c++ 容器适配器
Container //创建一个命名空间,避免和库里的冲突 namespace chen {//写一个模版template<class T, class Container deque<T>>//开始写我们的类class stack{public:void push(const T& x){_con.push_back(x);}void pop(){_con.pop_back();}const …...

正则表达式的应用领域及基本语法解析
目录 一、正则表达式的应用领域 1. 文本搜索和替换 2. 表单验证 3. 数据提取和分析 4. 数据清洗和处理 5. URL路由和路由匹配 二、正则表达式的基本语法 1. 字符匹配 2. 元字符和字符类 3. 量词和边界 4. 分组和捕获 5. 转义字符 三、常见正则表达式示例 1. 邮箱…...
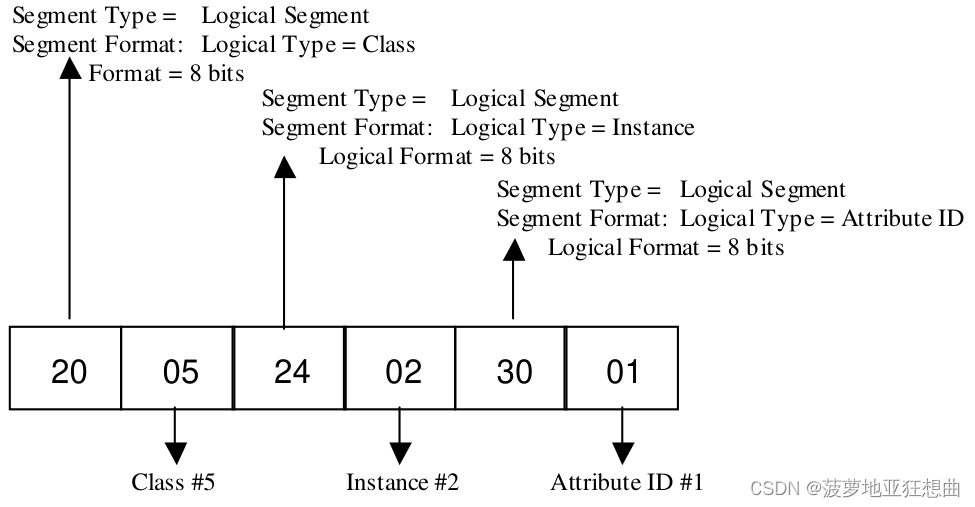
CIP或者EtherNET/IP中的PATH是什么含义?
目录 SegmentPATH举例 最近在学习EtherNET/IP,PATH不太明白,翻了翻规范,在这里记个笔记。下面的叙述可能是中英混合,有一些是规范中的原文我直接搬过来的。我翻译的不准确。 Segment PATH是CIP Segment中的一个分类。要了解PATH…...
)
使用lombok进行bulider之后调取HashMap的自定义方法进行对象操作报空指针异常(pojo也适用)
概论 这主要的问题就是bulider的特性的问题,就是他只能给你搭建了一个脚手架,里面的东西其实他没动你的,你得自己去给他实体化,如果你使用了类似HashMap等集合的话,你得自己去bulid一个在那个里面作为初始化对象你才可…...
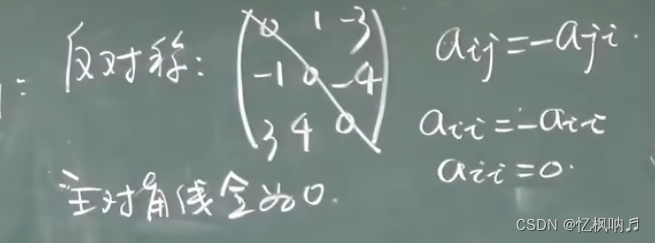
矩阵-day14
...

上古神器:十六位应用程序 Debug 的基本使用
文章目录 参考环境上古神器 DebugBug 与 DebuggingDebugDebug 应用程序淘汰原因使用限制 DOSBox学习 Debug 的必要性DOSBox-X Debug 的基本使用命令 R查看寄存器的状态修改寄存器的内容 命令 D显示内存中的数据指定起始内存空间地址指定内存空间的范围 命令 A使用命令语法错误查…...
[学习笔记]ARXML - Data Format
参考AUTOSAR文档: https://www.autosar.org/fileadmin/standards/R22-11/FO/AUTOSAR_TPS_ARXMLSerializationRules.pdfhttps://www.autosar.org/fileadmin/standards/R22-11/FO/AUTOSAR_TPS_ARXMLSerializationRules.pdf 编码 arxml只允许使用UTF-8编码ÿ…...
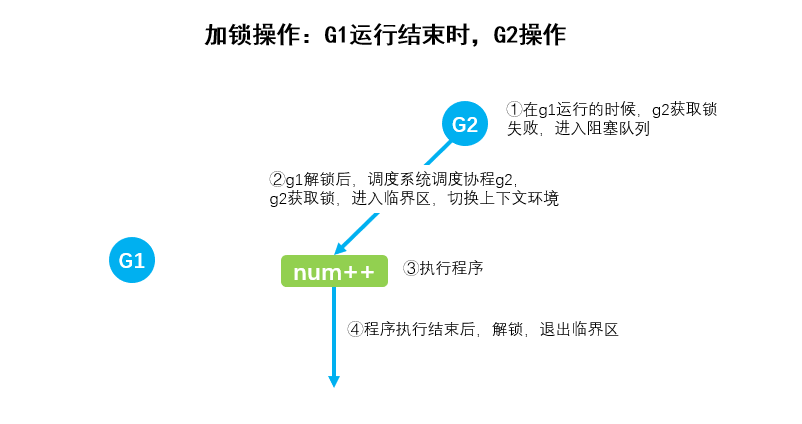
Go_原子操作和锁
原子操作和锁 本文先探究并发问题,再探究锁和原子操作解决问题的方式,最后进行对比。 并发问题 首先,我们看一下程序 num该程序表面看上去一步就可以运行完成,但是实际上,在计算机中是分三步运行的,如下…...

初识Java 12-1 流
目录 Java 8对流的支持 流的创建 随机数流 int类型的区间范围 generate() iterate() 流生成器 Arrays 正则表达式 本笔记参考自: 《On Java 中文版》 ||| 流的概念:流是一个与任何特定的存储机制都没有关系的元素序列。 流与对象的成批处理有关…...

【软件工程_UML—StartUML作图工具】startUML怎么画interface接口
StartUML作图工具怎么画interface接口 初试为圆形 ,点击该接口在右下角的设置中->Format->Stereotype Display->Label,即可切换到想要的样式 其他方式 在class diagram下,左侧有interface图标,先鼠标左键选择࿰…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

DeepSeek源码深度解析 × 华为仓颉语言编程精粹——从MoE架构到全场景开发生态
前言 在人工智能技术飞速发展的今天,深度学习与大模型技术已成为推动行业变革的核心驱动力,而高效、灵活的开发工具与编程语言则为技术创新提供了重要支撑。本书以两大前沿技术领域为核心,系统性地呈现了两部深度技术著作的精华:…...

Unity中的transform.up
2025年6月8日,周日下午 在Unity中,transform.up是Transform组件的一个属性,表示游戏对象在世界空间中的“上”方向(Y轴正方向),且会随对象旋转动态变化。以下是关键点解析: 基本定义 transfor…...

k8s从入门到放弃之HPA控制器
k8s从入门到放弃之HPA控制器 Kubernetes中的Horizontal Pod Autoscaler (HPA)控制器是一种用于自动扩展部署、副本集或复制控制器中Pod数量的机制。它可以根据观察到的CPU利用率(或其他自定义指标)来调整这些对象的规模,从而帮助应用程序在负…...

Xcode 16 集成 cocoapods 报错
基于 Xcode 16 新建工程项目,集成 cocoapods 执行 pod init 报错 ### Error RuntimeError - PBXGroup attempted to initialize an object with unknown ISA PBXFileSystemSynchronizedRootGroup from attributes: {"isa">"PBXFileSystemSynchro…...

用 Rust 重写 Linux 内核模块实战:迈向安全内核的新篇章
用 Rust 重写 Linux 内核模块实战:迈向安全内核的新篇章 摘要: 操作系统内核的安全性、稳定性至关重要。传统 Linux 内核模块开发长期依赖于 C 语言,受限于 C 语言本身的内存安全和并发安全问题,开发复杂模块极易引入难以…...
