【数据结构】堆的应用-----TopK问题
目录
一、前言
二、Top-k问题
💦解法一:暴力排序
💦解法二:建立N个数的堆
💦解法三:建立K个数的堆(最优解)
三、完整代码和视图
四、共勉
一、前言
在之前的文章中,已经详细的讲解了二叉树、堆、堆排序。那么关于堆还有一个比较有意思的题,就是TopK问题。
如果对堆和二叉树还不够了解的可以看看我之前的文章哦!!!
详解二叉树和堆
二、Top-k问题
Top-k问题:在 N 个数中,找出前 K 个(最大/最小)的元素,一般情况下数据量 N 都远大于 k。
Top-k问题在生活中是非常的常见,比如游戏中某个大区某个英雄熟练度最高的前10个玩家的排名,我们就要根据每个玩家对该英雄的熟练度进行排序,可能有200万个玩家,但我只想选出前10个,要对所有人去排个序吗?显然没这个必要。
再比如:专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。
💦解法一:暴力排序
对于Top-K问题,首先想到的最简单直接的方式就是排序。
我们用堆排序,其时间复杂度为:O(N*log2N)。
但是:如果数据量非常大,排序就不太可取了(可能数据都不能一下子全部加载到内存中)。
💦解法二:建立N个数的堆
建一个 N 个数的堆(C++中可用优先级队列priority_queue),不断的选数,选出前 k 个。
时间复杂度:建N个数的堆为O(N),获取堆顶元素 (也即是最值) 并删除掉堆顶元素为O(log2N),上述操作重复 k 次,所以时间复杂度为O(N+k*log2N)。
【思考】
能否再优化一下呢?假设 N 是 10 亿数,内存中放不下,是放在文件中的。前面两个方法都不能用了。
💦解法三:建立K个数的堆(最优解)
✨基本思想:
用数据集合中前K个元素来建堆。
找前 k 个最大的元素,则建小堆
找前 k 个最小的元素,则建大堆
用剩余的 N-K 个元素依次与堆顶元素来比较,不满足则删除堆顶元素,再插入。
找前 k 个最大的元素,大于堆顶元素,则删除堆顶元素,再插入
找前 k 个最小的元素,小于堆顶元素,则删除堆顶元素,再插入
将剩余的 N-K 个元素依次与堆顶元素比完之后,堆中剩余的K个元素就是所求的前K个最小或者最大的元素。
✨时间复杂度:▶ 建 k 个元素的堆为O(K);
▶ 遍历剩余的 N-K 个元素的时间代价为O(N-K),假设运气很差,每次遍历都入堆调整;
▶ 入堆调整:删除堆顶元素和插入元素都为O(log2K);
▶ 所以时间复杂度为O(k + (N-K)log2K)。当 N 远大于 K 时,为O(N*log2K),这种解法更优。
✨假如要找出最大的前 10 个数:
▶ 建立 10 个元素的小堆,数据集合中前 10 个元素依次放入小堆,此时的堆顶元素是堆中最小的元素,也是堆里面第 10 个最小的元素,
▶ 然后把数据集合中剩下的元素与堆顶比较,若大于堆顶则去掉堆顶,再将其插入,
▶ 这样一来,堆里面存放的就是数据集合中的前 10 个最大元素,
此时小堆的堆顶元素也就是堆中的第 10 个最大的元素
✨思考:为什么找出最大的前10个数,不能建大堆呢?
如果你建的10个元素的大堆,堆顶元素恰好是数据集合中最大的那个,那第2大的数、第3大的数不就能找不到了。
三、完整代码和视图
以从1w个数里找出最大的前10个数为例:
#include <stdio.h> #include <stdlib.h> #include <assert.h> #include <stdbool.h>typedef int HPDatatype; void Swap(HPDatatype* x, HPDatatype* y) {HPDatatype temp = 0;temp = *x;*x = *y;*y = temp; }void AdjustDown(HPDatatype* a,int n,int parent) {// 左孩子int child = parent * 2 + 1;// 防止越界while (child < n){//小堆if (child + 1 < n && a[child] > a[child + 1]){child++;}// 开始向下调整if (a[child] < a[parent]){Swap(&a[child], &a[parent]);parent = child;child = parent * 2 + 1;}else{break;}} }void TopK(HPDatatype* a, int n, int k) {HPDatatype* kminHeap = (HPDatatype*)malloc(sizeof(HPDatatype) * k);assert(kminHeap);// 1. 建堆----用a中前k个元素建堆for (int i = 0; i < k; i++){kminHeap[i] = a[i];}// 建小堆for (int j = ((n - 1) - 1) / 2; j >= 0; j--){// 从倒数第一个非叶子节点开始AdjustDown(kminHeap, k, j);}// 2. 将剩余n-k个元素依次与堆顶的元素交换,比堆顶大,交换for (int i = k; i < n; i++){if (a[i] > kminHeap[0]){kminHeap[0] = a[i];//如果比堆顶大,就替换AdjustDown(kminHeap, k, 0);//向下调整确保为堆}}for (int j = 0; j < k; j++){printf("%d ", kminHeap[j]);}printf("\n");free(kminHeap); }int main() {int n = 10000;int* a = (int*)malloc(sizeof(int) * n);srand(time(0));for (int i = 0; i < n; ++i){a[i] = rand() % 1000000; //产生一个随机数,数值均小于100万}a[5] = 1000000 + 1;a[1231] = 1000000 + 2;a[531] = 1000000 + 3;a[5121] = 1000000 + 4;a[115] = 1000000 + 5;a[2335] = 1000000 + 6;a[9999] = 1000000 + 7;a[76] = 1000000 + 8;a[423] = 1000000 + 9;a[3144] = 1000000 + 10;TopK(a, n, 10);return 0; }
四、共勉
以下就是我对数据结构---堆排序的理解,如果有不懂和发现问题的小伙伴,请在评论区说出来哦,同时我还会继续更新对数据结构-------链式二叉树,请持续关注我哦!!!!

相关文章:

【数据结构】堆的应用-----TopK问题
目录 一、前言 二、Top-k问题 💦解法一:暴力排序 💦解法二:建立N个数的堆 💦解法三:建立K个数的堆(最优解) 三、完整代码和视图 四、共勉 一、前言 在之前的文章中ÿ…...

QT之xml文件的读写
QT之xml文件的读写 简介用法举例 简介 QT的QDomDocument、QDomElement、QDomNode是Qt XML模块中的三个类,用于解析和操作XML文档。 1)QDomDocument类: QDomDocument类表示整个XML文档。它提供了解析XML文档的方法,如setContent(…...

C语言中的异常处理机制是什么?
C语言中的异常处理机制 C语言是一门强大而灵活的编程语言,它为程序员提供了广泛的控制权和自由度。然而,C语言本身并不提供像其他高级语言一样的内置异常处理机制,如Java中的try-catch或Python中的异常处理。因此,C语言程序员需要…...

Java中的并发编程模型和常用工具类
本文主要介绍了Java中的并发编程模型和常用工具类,首先阐述了并发编程的概念及其重要性,然后详细介绍了线程的基本概念、生命周期和状态转换、同步与互斥、死锁问题以及线程池的使用和实现原理。接着介绍了synchronized关键字和Lock接口的使用、原子变量…...
第10章 MySQL(一)
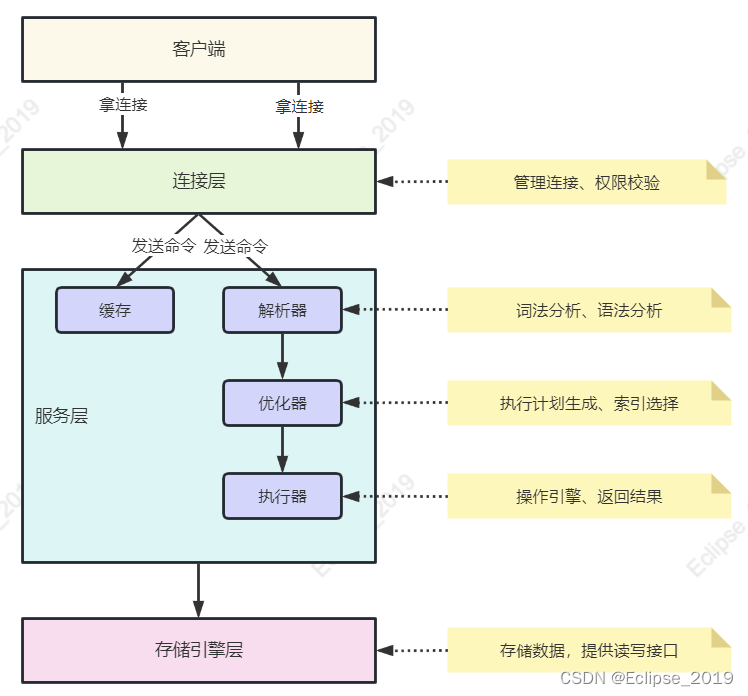
10.1 谈谈MySQL的架构 难度:★★ 重点:★ 白话解析 要想彻底的理解MySQL,它的架构一定要先弄清楚,当Java程序员通过JDBC或者Mybatis去执行一条SQL的时候,到底经历了什么。下边先看一幅图: 户端:Java程序员通过JDBC或者Mybatis去拿MySQL的驱动程序,实际上就是拿客户端。…...
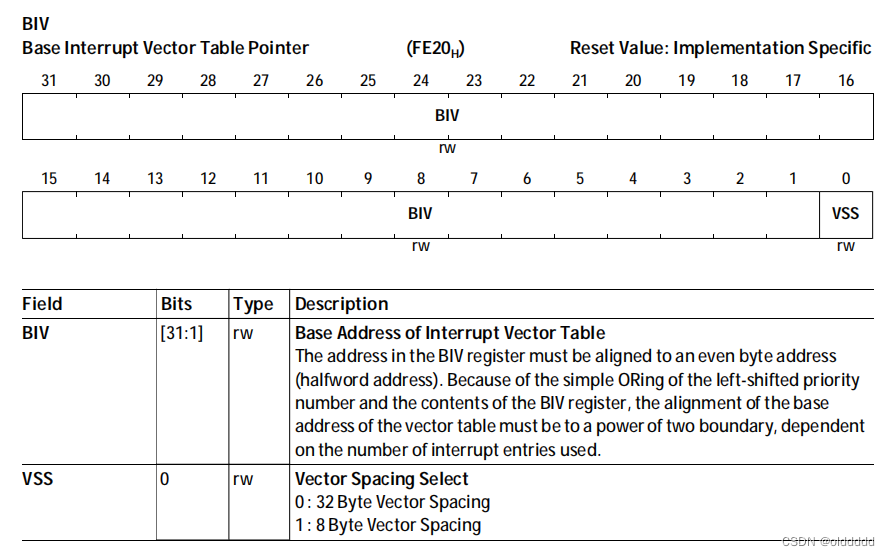
英飞凌 Tricore 架构中断系统详解
本文以TC3系列MCU为例,先来了解中断源是如何产生的,再看一下CPU是如何处理中断源的。 AURIX TC3XX的中断路由模块 Interrupt Router (IR) 在TC3中,中断既可以被CPU处理,也可以被DMA处理,所以手册中不再把中断称为中断…...

单例模式:饿汉式
单例模式全局仅一个实例,用于获取公共的内容 头文件mglobalinfomgr.h class MGlobalInfoMgr {MGlobalInfoMgr();~MGlobalInfoMgr(); public:static MGlobalInfoMgr* GetInstance(); private:static MGlobalInfoMgr* _instance; }; 源文件mglobalinfomgr.cpp MGl…...

什么是视图
目录 一、什么是视图 二、视图的作用 三、创建视图 四、使用视图 1.使用视图查询员工信息 五、注意事项 六、补充 一、什么是视图 视图是基于查询的虚拟表,是一个逻辑表,本身并不包含数据。同真实的表一样,视图包含一系列带有名称的列…...
C++——list(2)
作者:几冬雪来 时间:2023年9月28日 内容:C——list内容讲解 目录 前言: list的const迭代器: const的iterator: const迭代器: operator->: 拷贝构造: 迭代器接口补充&…...

Django基础讲解-路由控制器和视图(Django-02)
一 路由控制器 参考链接: Django源码阅读:路由(二) - 知乎 Route路由, 是一种映射关系!路由是把客户端请求的 url路径与视图进行绑定 映射的一种关系。 这个/timer通过路由控制器最终匹配到myapp.views中的视图函数 …...

【算法题】2873. 有序三元组中的最大值 I
题目: 给你一个下标从 0 开始的整数数组 nums 。 请你从所有满足 i < j < k 的下标三元组 (i, j, k) 中,找出并返回下标三元组的最大值。如果所有满足条件的三元组的值都是负数,则返回 0 。 下标三元组 (i, j, k) 的值等于 (nums[i]…...

HTML5 跨屏前端框架 Amaze UI
Amaze UI采用国际最前沿的“组件式开发”以及“移动优先”的设计理念,基于其丰富的组件,开发者可通过简单拼装即可快速构建出HTML5网页应用,上线仅半年,Amaze UI就成为了国内最流行的前端框架,目前在Github上收获Star数…...
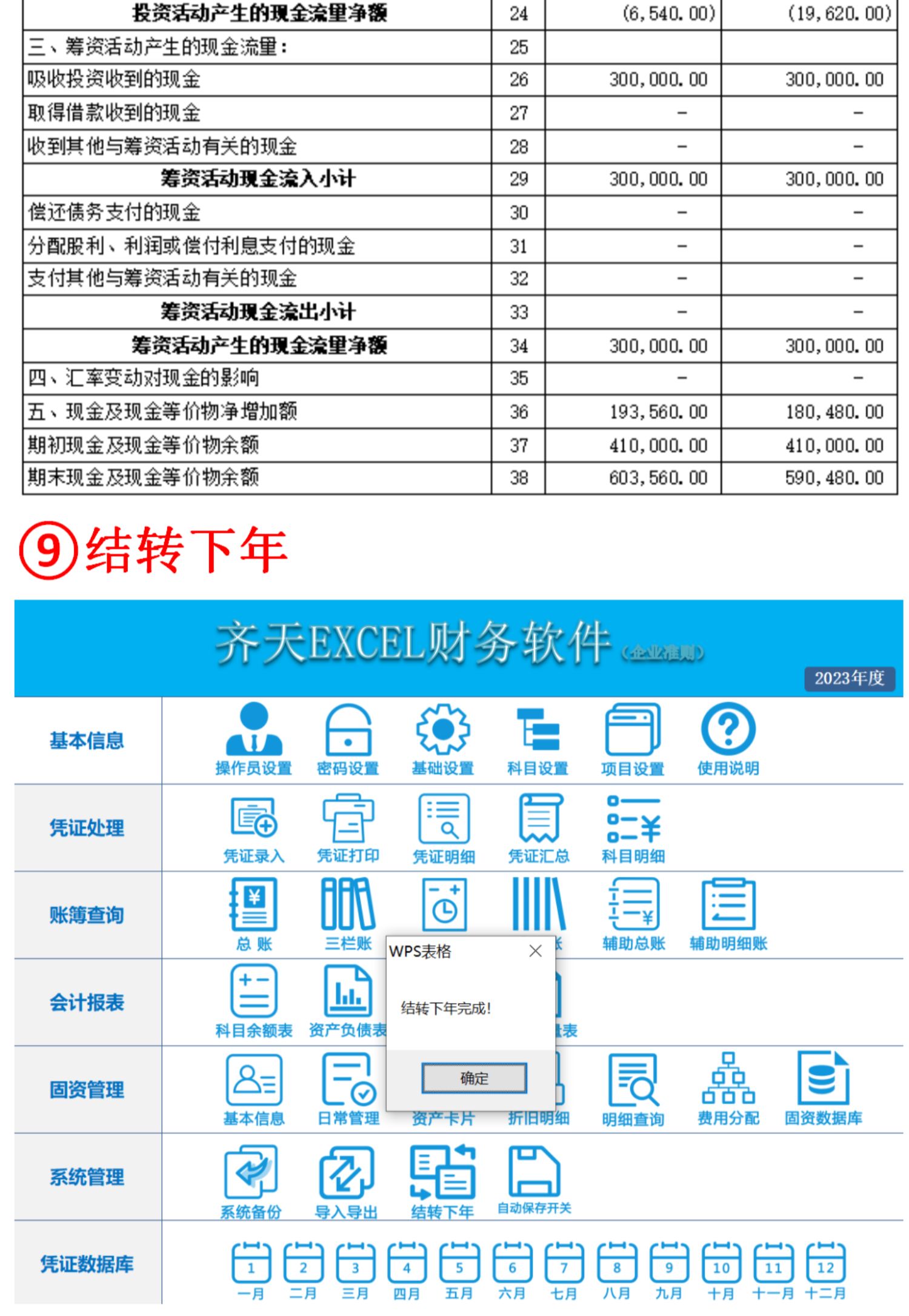
EXCEL会计记账报表财务软件企业公司做账系统凭证自动生成报表
本系统基于VBA编程设计,具有界面简洁美观,操作方便快捷,功能完备实用的特点,系统分为基本信息、凭证处理、账簿查询、会计报表、固定资产管理、系统管理、凭证数据库七大模块,您只需要录入记账凭证,就可以自…...

Can‘t pickle <class ‘__main__.Test‘>: it‘s not the same object as __main__.Test
目录 原因1 类名重复了 案例1 变量名和类名重复 原因1 类名重复了 检查项目代码,是不是其他地方有同名类。 案例1 变量名和类名重复 转自:python3报错Cant pickle <class __main__.Test>: its not the same object as __main__.Test解决 - 知乎…...

第九章 动态规划 part14 1143. 最长公共子序列 1035. 不相交的线 53. 最大子序和
第五十六天| 第九章 动态规划 part14 1143. 最长公共子序列 1035. 不相交的线 53. 最大子序和 一、1143. 最长公共子序列 题目链接: 题目介绍: 思路: 本题和“最长重复子数组”区别在于**这里不要求是连续的了,但要有相对顺序*…...
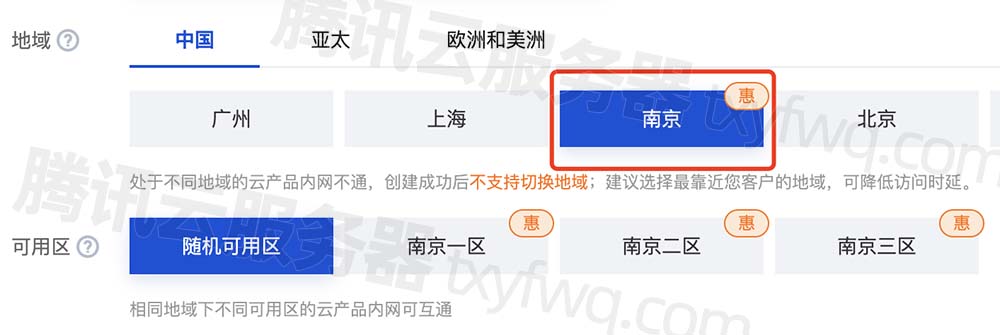
腾讯云服务器南京地域详细介绍、测试IP和Ping值测速
腾讯云服务器南京地域怎么样?南京地域很不错,正好处于中间的位置,南方北方用户均可以选择,网络延迟更低速度更快,并且目前南京地域有活动,南京地域可用区可选南京一区、南京二区和南京三区,腾讯…...

理解CSS的层叠性和继承性
CSS的层叠性(cascading)指的是在同一元素上应用多个样式时,不同样式之间的优先级别以及如何进行组合和冲突解决的规则。具体来说,CSS采用的是“选择器优先级”规则来判断哪个样式优先级更高,如果多个样式的优先级相同&…...
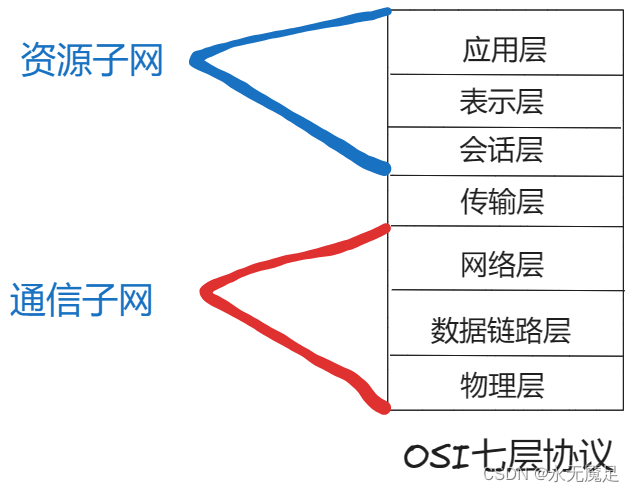
OSI体系结构和TCP/IP体系结构
在第一章( 计网第一章 )的时候,曾经提到过OSI体系结构和TCP/IP体系结构,并对它们进行了简单的对比。这篇博客在其基础上进行更深层次的理解。 一.OSI体系结构: 通信子网: 计算机网络在逻辑功能上可以分为…...

侯捷 C++ STL标准库和泛型编程 —— 8 适配器
8 适配器 适配器 Adapter 只是一个小变化,比如改个接口,函数名称等等其出现在三个地方:仿函数适配器,迭代器适配器,容器适配器可以使用继承 / 复合的两种方式实现,STL中都用复合 其思想就是将该记的东西记…...
)
每日一题 416 分割等和子集(01背包)
题目 分割等和子集 给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。 示例 1: 输入:nums [1,5,11,5] 输出:true 解释:数组可以分割成 [1, 5, 5] …...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...

快速排序算法改进:随机快排-荷兰国旗划分详解
随机快速排序-荷兰国旗划分算法详解 一、基础知识回顾1.1 快速排序简介1.2 荷兰国旗问题 二、随机快排 - 荷兰国旗划分原理2.1 随机化枢轴选择2.2 荷兰国旗划分过程2.3 结合随机快排与荷兰国旗划分 三、代码实现3.1 Python实现3.2 Java实现3.3 C实现 四、性能分析4.1 时间复杂度…...

内窥镜检查中基于提示的息肉分割|文献速递-深度学习医疗AI最新文献
Title 题目 Prompt-based polyp segmentation during endoscopy 内窥镜检查中基于提示的息肉分割 01 文献速递介绍 以下是对这段英文内容的中文翻译: ### 胃肠道癌症的发病率呈上升趋势,且有年轻化倾向(Bray等人,2018&#x…...

深入理解 React 样式方案
React 的样式方案较多,在应用开发初期,开发者需要根据项目业务具体情况选择对应样式方案。React 样式方案主要有: 1. 内联样式 2. module css 3. css in js 4. tailwind css 这些方案中,均有各自的优势和缺点。 1. 方案优劣势 1. 内联样式: 简单直观,适合动态样式和…...

