第九章 动态规划 part14 1143. 最长公共子序列 1035. 不相交的线 53. 最大子序和
第五十六天| 第九章 动态规划 part14 1143. 最长公共子序列 1035. 不相交的线 53. 最大子序和
一、1143. 最长公共子序列
-
题目链接:
-
题目介绍:
-
思路:
-
本题和“最长重复子数组”区别在于**这里不要求是连续的了,但要有相对顺序**,即:“ace” 是 “abcde” 的子序列,但 “aec” 不是 “abcde” 的子序列。
-
dp五部曲:
-
(1)确定dp数组及下标含义:
-
dp[i][j]:表示的是以下标i-1为结尾的text1和以下标j-1为结尾的text2的最长公共子序列的长度
-
-
(2)确定递推公式:
-
本题不再要求连续,因此dp[i][j]可以由三个方向推出 -
如果text1[i - 1] 与 text2[j - 1]相同,那么找到了一个公共元素,所以dp[i][j] = dp[i - 1][j - 1] + 1;如果text1[i - 1] 与 text2[j - 1]不相同,那就看看text1[0, i - 2]与text2[0, j - 1]的最长公共子序列 和 text1[0, i - 1]与text2[0, j - 2]的最长公共子序列,取最大的。即:dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]); -

-
-
(3)初始化dp数组:
-
根据dp数组的含义,char1[0, i-1]和空数组的公共子序列长度为0;同理,char2[0, j-1]和空数组的公共子序列长度也为0。因此,dp[i][0] = 0,dp[0][j] = 0。其他位置在后续均可以覆盖,因此都初始化为0。
-
-
(4)确定遍历顺序:
- 根据递推公式可知是正序
-
-
和重复子数组(连续公共子序列)不同,本题的最终结果是在二维dp数组的最右下角,因为根据递推公式,如果不相同还是会根据左边的和上边的推导出来。
-
-
代码:
class Solution {public int longestCommonSubsequence(String text1, String text2) {char[] char1 = text1.toCharArray();char[] char2 = text2.toCharArray();// (1)确定dp数组及下标含义// dp[i][j]:表示的是以下标i-1为结尾的text1和以下标j-1为结尾的text2的最长公共子序列的长度int[][] dp = new int[char1.length + 1][char2.length + 1];// (3)初始化dp数组// 根据dp数组的含义,char1[0, i-1]和空数组的公共子序列长度为0;同理,char2[0, j-1]和空数组的公共子序列长度也为0。因此,dp[i][0] = 0,dp[0][j] = 0。其他位置在后续均可以覆盖,因此都初始化为0。// (4)确定遍历顺序// 根据递推公式可知是正序for (int i = 1; i <= char1.length; i++) {for (int j = 1; j <= char2.length; j++) {// (2)确定递推公式// 本题不再要求连续,因此dp[i][j]可以由三个方向推出if (char1[i-1] == char2[j-1]) {dp[i][j] = dp[i-1][j-1] + 1;} else {dp[i][j] = Math.max(dp[i-1][j], dp[i][j-1]);}}}// 和重复子数组(连续公共子序列)不同,本题的最终结果是在二维dp数组的最右下角,因为根据递推公式,如果不相同还是会根据左边的和上边的推导出来。return dp[char1.length][char2.length];}
}
二、1035. 不相交的线
-
题目链接:https://leetcode.cn/problems/uncrossed-lines/
-
题目介绍:
-
在两条独立的水平线上按给定的顺序写下
nums1和nums2中的整数。现在,可以绘制一些连接两个数字
nums1[i]和nums2[j]的直线,这些直线需要同时满足满足:nums1[i] == nums2[j]- 且绘制的直线不与任何其他连线(非水平线)相交。
请注意,连线即使在端点也不能相交:每个数字只能属于一条连线。
以这种方法绘制线条,并返回可以绘制的最大连线数。
示例 1:

输入:nums1 = [1,4,2], nums2 = [1,2,4] 输出:2 解释:可以画出两条不交叉的线,如上图所示。 但无法画出第三条不相交的直线,因为从 nums1[1]=4 到 nums2[2]=4 的直线将与从 nums1[2]=2 到 nums2[1]=2 的直线相交。
-
-
思路:
- 套壳的“最长公共子序列”
- 思路和解法与上道题目是一样的
-
代码:
class Solution {public int maxUncrossedLines(int[] nums1, int[] nums2) {int[][] dp = new int[nums1.length + 1][nums2.length + 1];for (int i = 1; i <= nums1.length; i++) {for (int j = 1; j <= nums2.length; j++) {if (nums1[i-1] == nums2[j-1]) {dp[i][j] = dp[i-1][j-1] + 1;} else {dp[i][j] = Math.max(dp[i-1][j], dp[i][j-1]);}}}return dp[nums1.length][nums2.length];}
}
三、53. 最大子序和
-
题目链接:https://leetcode.cn/problems/maximum-subarray
-
题目介绍:
-
相关企业
给你一个整数数组
nums,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。子数组 是数组中的一个连续部分。
示例 1:
输入:nums = [-2,1,-3,4,-1,2,1,-5,4] 输出:6 解释:连续子数组 [4,-1,2,1] 的和最大,为 6 。
-
-
思路:
-
dp五部曲:
-
(1)确定dp数组及下标含义
-
dp[i]:表示的是以nums[i]为结尾的最大连续子序列之和
-
-
(2)确定递推公式
-
dp[i]只能由两个方向推出来:一个是:因为是连续的所以是dp[i-1] + nums[i]另一个是:当前nums[i]
-
-
(3)初始化dp数组
-
dp[0]:表示的是以nums[0]为结尾的最大连续子序列的和,所以dp[0] = nums[0]
-
-
(4)遍历顺序:正序
-
-
-
代码:
class Solution {public int maxSubArray(int[] nums) {if (nums == null || nums.length == 0) return 0;int result = nums[0];// (1)确定dp数组及下标含义// dp[i]:表示的是以nums[i]为结尾的最大连续子序列之和int[] dp = new int[nums.length];// (3)初始化dp数组// dp[0]:表示的是以nums[0]为结尾的最大连续子序列的和,所以dp[0] = nums[0].dp[0] = nums[0];// (4)遍历顺序:正序for (int i = 1; i < nums.length; i++) {// (2)确定递推公式// dp[i]只能由两个方向推出来:// 一个是:因为是连续的所以是dp[i-1] + nums[i]// 另一个是:当前nums[i]dp[i] = Math.max(dp[i-1] + nums[i], nums[i]);if (dp[i] > result) result = dp[i];}return result;}
}
总结:
- 子数组:求解的就是**连续子序列**
- 子序列:没有强调的连续,只要是子序列即可
相关文章:

第九章 动态规划 part14 1143. 最长公共子序列 1035. 不相交的线 53. 最大子序和
第五十六天| 第九章 动态规划 part14 1143. 最长公共子序列 1035. 不相交的线 53. 最大子序和 一、1143. 最长公共子序列 题目链接: 题目介绍: 思路: 本题和“最长重复子数组”区别在于**这里不要求是连续的了,但要有相对顺序*…...
腾讯云服务器南京地域详细介绍、测试IP和Ping值测速
腾讯云服务器南京地域怎么样?南京地域很不错,正好处于中间的位置,南方北方用户均可以选择,网络延迟更低速度更快,并且目前南京地域有活动,南京地域可用区可选南京一区、南京二区和南京三区,腾讯…...

理解CSS的层叠性和继承性
CSS的层叠性(cascading)指的是在同一元素上应用多个样式时,不同样式之间的优先级别以及如何进行组合和冲突解决的规则。具体来说,CSS采用的是“选择器优先级”规则来判断哪个样式优先级更高,如果多个样式的优先级相同&…...
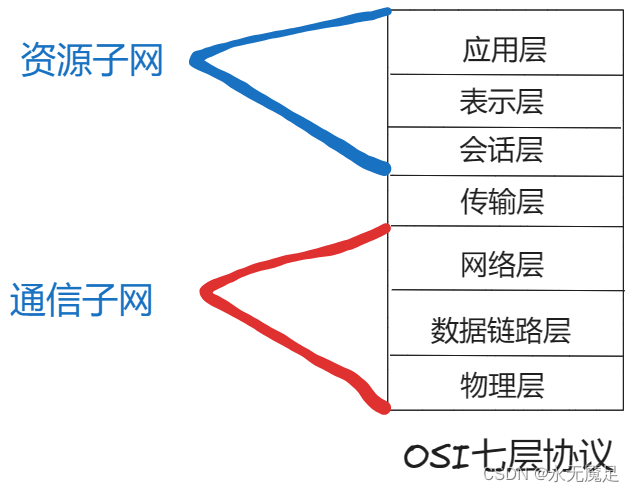
OSI体系结构和TCP/IP体系结构
在第一章( 计网第一章 )的时候,曾经提到过OSI体系结构和TCP/IP体系结构,并对它们进行了简单的对比。这篇博客在其基础上进行更深层次的理解。 一.OSI体系结构: 通信子网: 计算机网络在逻辑功能上可以分为…...

侯捷 C++ STL标准库和泛型编程 —— 8 适配器
8 适配器 适配器 Adapter 只是一个小变化,比如改个接口,函数名称等等其出现在三个地方:仿函数适配器,迭代器适配器,容器适配器可以使用继承 / 复合的两种方式实现,STL中都用复合 其思想就是将该记的东西记…...
)
每日一题 416 分割等和子集(01背包)
题目 分割等和子集 给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。 示例 1: 输入:nums [1,5,11,5] 输出:true 解释:数组可以分割成 [1, 5, 5] …...
U盘插上就显示让格式化是坏了吗?
U盘以其体积小巧、存储容量大、读写速度快的特点,在各种工作和个人使用场合中得到了广泛应用,因此深得用户好评。然而,在日常使用U盘的过程中,经常会遇到一些问题和挑战。今天,我将为大家详细解释U盘出现要求格式化的现…...
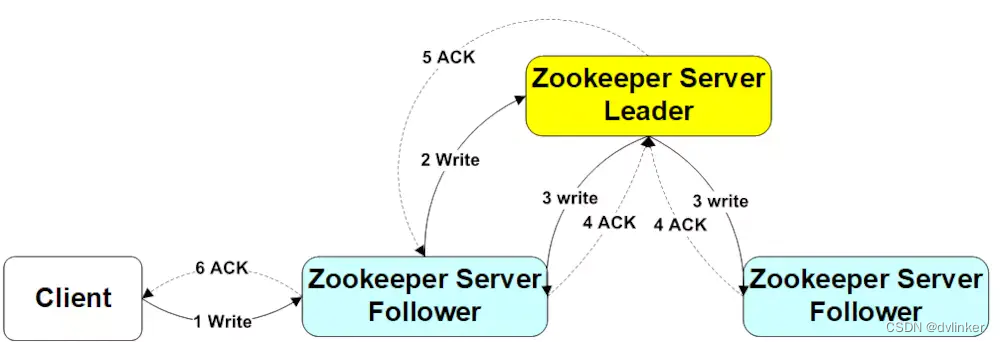
分布式应用程序协调服务 ZooKeeper 详解
目录 1、ZooKeeper简介 2、ZooKeeper的使用场景 3、ZooKeeper设计目的 4、ZooKeeper数据模型 5、ZooKeeper几个重要概念 5.1、ZooKeeper Session 5.2、ZooKeeper Watch 5.3、Consistency Guarantees 6、ZooKeeper的工作原理 6.1、Leader Election 6.2、Leader工作流…...
)
Anniversary party(树形dp 基础题)
1.题目大意 There is going to be a party to celebrate the 80-th Anniversary of the Ural State University. The University has a hierarchical structure of employees. It means that the supervisor relation forms a tree rooted at the rector V. E. Tretyakov. In …...
Junit的常用操作
注:本篇文章讲解的是junit5 目录 Juint是什么 Juint需要导入的依赖 Juint常用注解 Junit执行顺序 参数化 断言 测试套件 Juint是什么 Juint 是 Java 的一个单元测试框架. 也是回归测试框架. 使用 Junit 能让我们快速的完成单元测试。 注意:Junit 测试也是程序…...
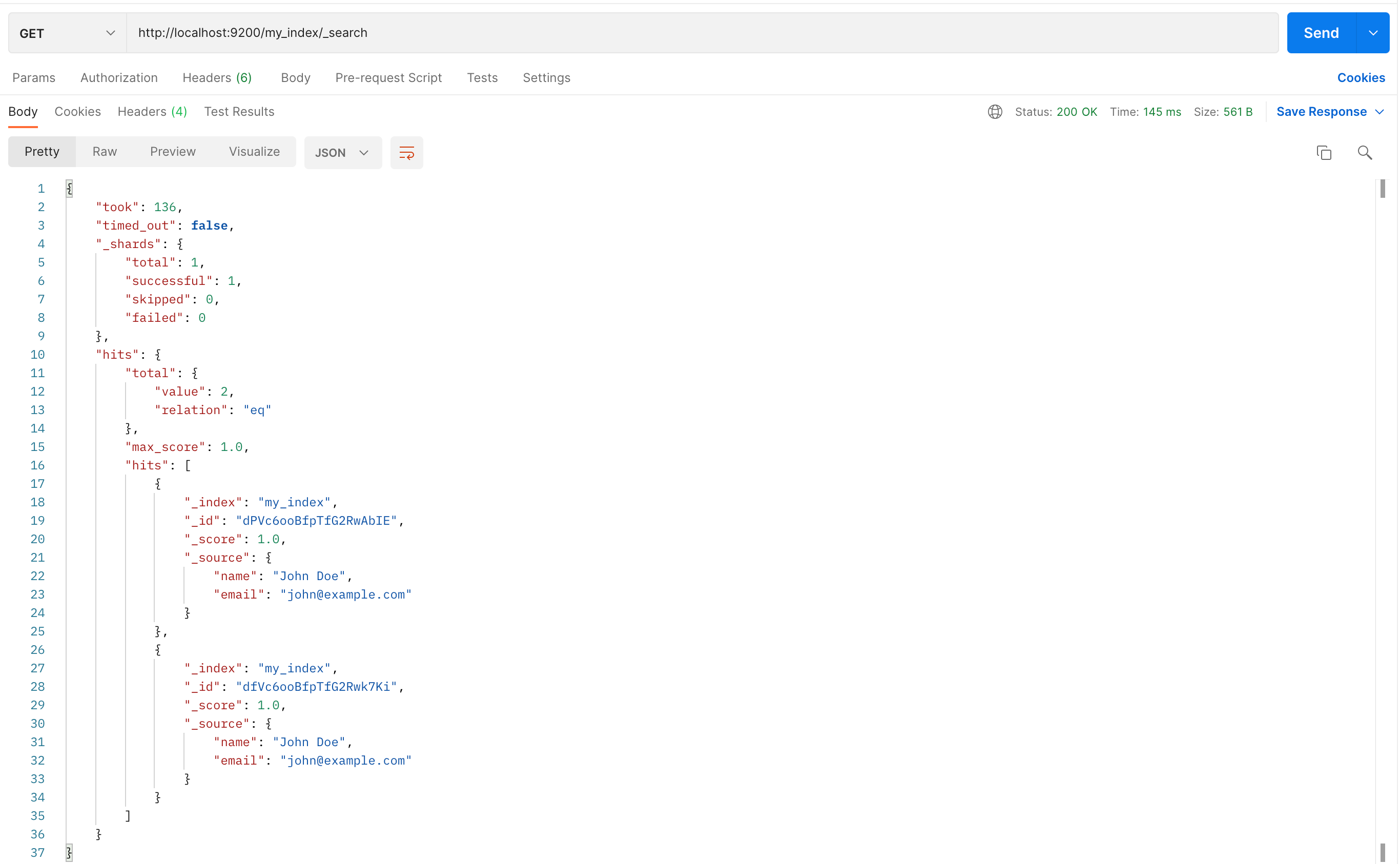
Elasticsearch安装并使用Postman访问
Elasticsearch,一个强大的开源搜索和分析引擎,已经在全球范围内被广泛应用于各种场景,包括网站搜索、日志分析、实时应用等。由于其强大的功能和灵活性,Elasticsearch 已经成为大数据处理的重要工具。然而,对于许多初次…...

Pytorch深度学习训练模型保存问题,找不到保存路径
执行torch.save(net.state_dict(), save_path_pth)报错: RuntimeError: Parent directory D:\xxxxxxxxxxx\weights does not exist. 将文件路径的中文改成全英文就可以了。 注意:这个代码在torch1.7版本无报错,但是在1.13.1版本报错。在linu…...
)
数据结构与算法之堆: Leetcode 23. 合并 K 个升序链表 (Typescript版)
合并 K 个升序链表 https://leetcode.cn/problems/merge-k-sorted-lists/ 描述 给你一个链表数组,每个链表都已经按升序排列请你将所有链表合并到一个升序链表中,返回合并后的链表 示例 1 输入:lists [[1,4,5],[1,3,4],[2,6]] 输出&…...
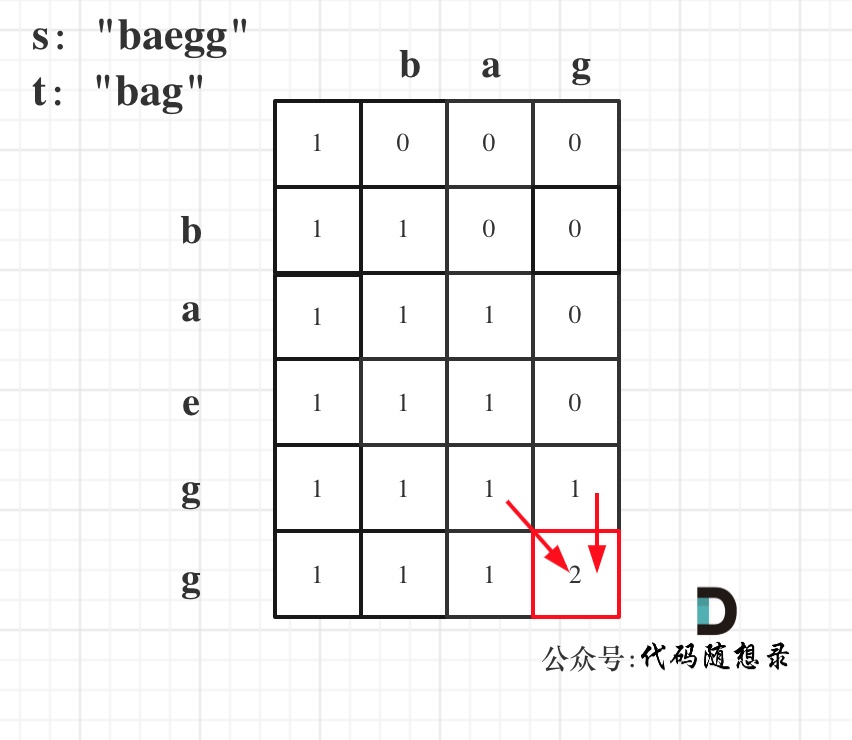
代码随想录算法训练营第五十七天 | 392.判断子序列 115.不同的子序列
1. 判断子序列 392. 判断子序列 - 力扣(LeetCode) dp[i][j] 表示以下标i-1为结尾的字符串s,和以下标j-1为结尾的字符串t,相同子序列的长度。 class Solution {public boolean isSubsequence(String s, String t) {//dp[i][j] 表示…...
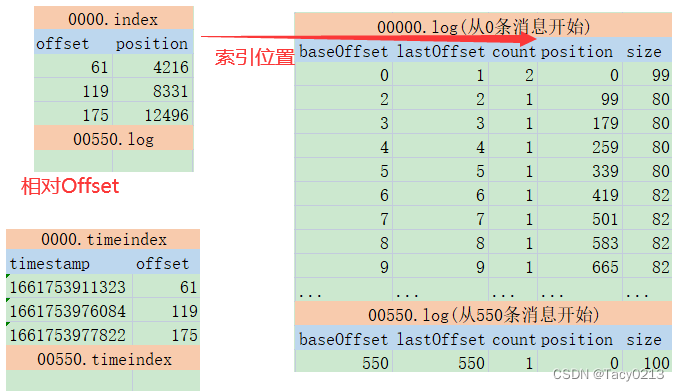
Kafka日志索引详解以及生产常见问题分析与总结
文章目录 1、Kafka的Log日志梳理1.1、Topic下的消息是如何存储的?1.1.1、 log文件追加记录所有消息1.1.2、 index和timeindex加速读取log消息日志。 1.2、文件清理机制1.2.1、如何判断哪些日志文件过期了1.2.2、过期的日志文件如何处理 1.3、Kafka的文件高效读写机制…...

vue中 css scoped原理
Vue中css的逻辑是先放子组件,然后放父组件,所以同样的css类名,子组件会被父组件覆盖 html 如下 子被父覆盖 scoped是通过给组件加hash值,锁定组件。 父子组件均scoped的情况下,子仍会覆盖 还是被覆盖了 如何避免被…...
)
tf.compat.v1.global_variables()
tf.global_variables tf.global_variables() 是 TensorFlow 1.x 中的一个函数,它返回图中所有的全局变量。在 TensorFlow 2.x 中,这个函数已经被移除了,取而代之的是 tf.compat.v1.global_variables()。 然而,在 TensorFlow 2.x …...

登录注册实现
一、前端页面注册到Vue 1.创建登录和注册组件 <template><div>login</div></template><script> export default {name: HomeView,data() {return {}},methods: {}, } </script><template><div>register</div></tem…...

Push rejected: Push to origin/master was rejected
Push rejected: Push to origin/master was rejected 原因:推拒绝:推送到起源/主人被拒绝 解决方案如下: 方案1: 1.在Idea打开终端 方案2: 1、在对应项目文件里打开 Git Bash 然后依次输入: git pull …...

在线OJ项目核心思路
文章目录 在线OJ项目核心思路1. 项目介绍2.预备知识理解多进程编程为啥采用多进程而不使用多线程?标准输入&标准输出&标准错误 3.项目实现题目API实现相关实体类定义新增/修改题目获取题目列表 编译运行编译运行流程 4.统一功能处理 在线OJ项目核心思路 1. 项目介绍 …...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

C# 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...

android RelativeLayout布局
<?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...
