AtCoder Beginner Contest 233 (A-Ex)
A.根据题意模拟即可
B.根据题意模拟即可
C.直接用map 进行dp即可
D.用前缀和进行模拟,用map统计前缀和,每次计算当前前缀和-k的个数就是以当前点为右端点答案。
E - Σ[k=0..10^100]floor(X/10^k) (atcoder.jp)
(1)题意

(2)思路
手动推一下这个东西就会发现,其实每一位上的贡献等于这一位后面的所有数加起来,因此做一个后缀和即可。
(3)代码
#include <bits/stdc++.h>
#define rep(i,z,n) for(int i = z;i <= n; i++)
#define per(i,n,z) for(int i = n;i >= z; i--)
#define PII pair<int,int>
#define fi first
#define se second
#define vi vector<int>
#define vl vector<ll>
#define pb push_back
#define sz(x) (int)x.size()
#define all(x) (x).begin(),(x).end()
using namespace std;
using ll = long long;
const int N = 5e5 + 10;
ll Ans[N],suf[N];
void solve()
{string x;cin >> x;reverse(all(x));for(int i = sz(x) - 1;i >= 0;i --) suf[i] = suf[i + 1] + (x[i] - '0');for(int i = 0;i < sz(x);i ++) {Ans[i] = suf[i]; } for(int i = 0;i < 500001;i ++) {Ans[i + 1] += Ans[i] / 10;Ans[i] %= 10;}int r = 500001;while(Ans[r] == 0) r --;while(r >= 0) cout << Ans[r --];
}
int main()
{ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);int T = 1;// cin >> T;while(T --) solve();return 0;
}F - Swap and Sort (atcoder.jp)
(1)题意
有一个排列P,给出M组交换关系,第i组swap(Pai,Pbi),问是否有可能可以使P不降。
(2)思路
首先,若i和P[i]不在一个连通块,则一定不会交换成功,然后考虑如何交换,对于度数为1的点说明我们此时交换掉他并且不会影响后继,因此满足拓扑排序,那么我们直接根据拓扑排序进行交换即可。
(3)代码
#include <bits/stdc++.h>
#define rep(i,z,n) for(int i = z;i <= n; i++)
#define per(i,n,z) for(int i = n;i >= z; i--)
#define PII pair<int,int>
#define fi first
#define se second
#define vi vector<int>
#define vl vector<ll>
#define pb push_back
#define sz(x) (int)x.size()
#define all(x) (x).begin(),(x).end()
using namespace std;
using ll = long long;
const int N = 2e5 + 10;
struct DSU {vector<int> f,siz;int n;DSU(int _n) {n = _n;f.resize(n + 1);siz.resize(n + 1,1);iota(f.begin(),f.end(),0);}inline int find(int x) {if(x == f[x]) return x;return f[x] = find(f[x]);}inline bool same(int x,int y) {x = find(x),y = find(y);return x == y;}inline void merge(int x,int y) {if(same(x,y)) return ;x = find(x),y = find(y);siz[y] += siz[x];f[x] = y;}//目前连通块个数inline int connect() {int res = 0;for(int i = 1;i <= n;i ++) {res += (i == find(i));}return res;}//求某一个联通块得大小inline int count(int x) {x = find(x);return siz[x];}
};
int p[N],deg[N];
vector<PII> e[N];
vector<int> ans;
inline bool dfs(int u,int f,int tar)
{if(u == tar) return true;for(auto [v,id]: e[u]) {if(v == f) continue;if(dfs(v,u,tar)) {swap(p[u],p[v]);ans.pb(id);return true;}}return false;
}
void solve()
{int n;cin >> n;rep(i,1,n) cin >> p[i];DSU dsu(n);int m;cin >> m;rep(i,1,m) {int u,v;cin >> u >> v;if(!dsu.same(u,v)) {dsu.merge(u,v);e[u].pb({v,i});e[v].pb({u,i});deg[u] ++,deg[v] ++;}}queue<int> q;rep(i,1,n) {if(!dsu.same(i,p[i])) {cout << -1 << '\n';return;}if(deg[i] == 1) q.push(i);}while(!q.empty()) {int v = q.front();q.pop();int tar = 0;for(int i = 1;i <= n;i ++) {if(p[i] == v) {tar = i;break;}}if(!dfs(v,0,tar)) {cout << -1 << '\n';return;}for(auto [u,id]: e[v]) {if(-- deg[u] == 1) q.push(u);}}cout << sz(ans) << '\n';for(auto x : ans) cout << x << ' ';
}
int main()
{ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);int T = 1;// cin >> T;while(T --) solve();return 0;
}G - Strongest Takahashi (atcoder.jp)
(1)题意
给你一个N*N的矩形,里面#代表的是障碍,.不是障碍,你每次可以选择一个D*D的矩形把里面的障碍清除掉会花费D,问你把N*N的障碍全部清除掉的最小花费是多少。
(2)思路
很明显的一个思路是,这个可以分治进行dp,考虑dp[l1][r1][l2][r2]表示消除[l1-l2][r1-r2]这个矩形的最小花费,我们每一次可以枚举横着切下去还是竖着切下去就行,或者整个是正方形也可以直接清除,取个最小花费即可。
(3)代码
#include <bits/stdc++.h>
#define rep(i,z,n) for(int i = z;i <= n; i++)
#define per(i,n,z) for(int i = n;i >= z; i--)
#define PII pair<int,int>
#define fi first
#define se second
#define vi vector<int>
#define vl vector<ll>
#define pb push_back
#define sz(x) (int)x.size()
#define all(x) (x).begin(),(x).end()
using namespace std;
using ll = long long;
const int N = 55;
int dp[N][N][N][N],s[N][N];
string mp[N];
const int inf = 0x3f3f3f3f;
int get(int x1,int y1,int x2,int y2)
{return s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1];
}
inline int dfs(int x1,int y1,int x2,int y2)
{if(dp[x1][y1][x2][y2] != -1) return dp[x1][y1][x2][y2];if(get(x1,y1,x2,y2) == 0) return dp[x1][y1][x2][y2] = 0;int mi = inf;for(int i = x1 + 1;i <= x2;i ++) {mi = min(mi,dfs(x1,y1,i - 1,y2) + dfs(i,y1,x2,y2));}for(int i = y1 + 1;i <= y2;i ++) {mi = min(mi,dfs(x1,y1,x2,i - 1) + dfs(x1,i,x2,y2));}if(x2 - x1 == y2 - y1) mi = min(mi,x2 - x1 + 1);return dp[x1][y1][x2][y2] = mi;
}
void solve()
{int n;cin >> n;memset(dp,-1,sizeof(dp));rep(i,1,n) {cin >> mp[i];mp[i] = " " + mp[i];rep(j,1,n) s[i][j] = s[i - 1][j] + s[i][j - 1] + (mp[i][j] == '#') - s[i - 1][j - 1];}cout << dfs(1,1,n,n);
}
int main()
{ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);int T = 1;// cin >> T;while(T --) solve();return 0;
}Ex - Manhattan Christmas Tree (atcoder.jp)
(1)题意
二维平面上有N棵圣诞树,第i棵位于[xi,yi],要回答一下Q个问题,第i个问题是,以曼哈顿距离为单位,(ai,bi)和距离该点最近的Ki棵圣诞树之间的距离是多少?
(2)思路
考虑曼哈顿距离不好进行计算,因此转换成切比雪夫距离,源坐标系上(x,y)的曼哈顿距离等价于新坐标系上(x+y,x-y)的切比雪夫距离,(补充:源坐标系上(x,y)的切比雪夫距离等价于新坐标系上(,
)的曼哈顿距离)看着切比雪夫距离,我们很容易想到直接二分距离,问题转变这个矩形平面内有多少点,也就是二维数点问题,因为点不是很稠密,我们考虑直接动态开点二维树状数组。
(3)代码
#include <bits/stdc++.h>
#define rep(i,z,n) for(int i = z;i <= n; i++)
#define per(i,n,z) for(int i = n;i >= z; i--)
#define PII pair<int,int>
#define fi first
#define se second
#define vi vector<int>
#define vl vector<ll>
#define pb push_back
#define sz(x) (int)x.size()
#define all(x) (x).begin(),(x).end()
using namespace std;
using ll = long long;
const int N = 5e5 + 10;
vector<int> ver[N << 1];
inline int lowbit(int x)
{return x & (-x);
}
inline void add(int x,int y)
{x += N,y += N;if(!y) y = 1;while(y < 2 * N) {ver[y].pb(x);y += lowbit(y);}
}
inline int get(int y,int x1,int x2)
{int Ans = 0;y += N,x1 += N,x2 += N;if(y >= 2 * N) y = 2 * N - 1;while(y > 0) {Ans += upper_bound(all(ver[y]),x2) - lower_bound(all(ver[y]),x1);y -= lowbit(y);}return Ans;
}
inline int query(int x1,int y1,int x2,int y2)
{return get(y2,x1,x2) - get(y1 - 1,x1,x2);
}
void solve()
{vector<PII> point;int n;cin >> n;rep(i,1,n) {int x,y;cin >> x >> y;point.pb({x + y,x - y});}sort(all(point));for(auto [x,y]: point) add(x,y);int q;cin >> q;while(q --) {int x,y,k;cin >> x >> y >> k;int z = x;x = z + y,y = z - y;int l = 0,r = N;while(l <= r) {int m = (l + r) >> 1;if(query(x - m,y - m,x + m,y + m) < k) l = m + 1;else r = m - 1;}cout << l << '\n';}
}
int main()
{ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);int T = 1;// cin >> T;while(T --) solve();return 0;
}相关文章:
AtCoder Beginner Contest 233 (A-Ex)
A.根据题意模拟即可 B.根据题意模拟即可 C.直接用map 进行dp即可 D.用前缀和进行模拟,用map统计前缀和,每次计算当前前缀和-k的个数就是以当前点为右端点答案。 E - Σ[k0..10^100]floor(X/10^k) (atcoder.jp) (1)…...

解决caffe中的python环境安装的问题
由于caffe(GitHub - BVLC/caffe: Caffe: a fast open framework for deep learning.)使用的python版本是2.7,而非python3,所以安装的时候使用命令:sudo apt install python2.7进行安装。 而在安装python的各种包时&am…...
专业图像处理软件DxO PhotoLab 7 mac中文特点和功能
DxO PhotoLab 7 mac是一款专业的图像处理软件,它为摄影师和摄影爱好者提供了强大而全面的照片处理和编辑功能。 DxO PhotoLab 7 mac软件特点和功能 强大的RAW和JPEG格式处理能力:DxO PhotoLab 7可以处理来自各种相机的RAW格式图像,包括佳能、…...
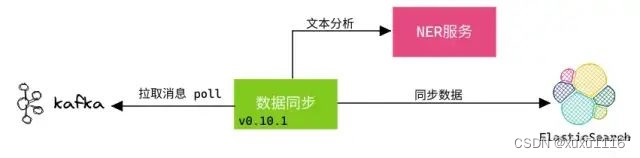
面试题:Kafka 为什么会丢消息?
文章目录 1、如何知道有消息丢失?2、哪些环节可能丢消息?3、如何确保消息不丢失? 引入 MQ 消息中间件最直接的目的:系统解耦以及流量控制(削峰填谷) 系统解耦: 上下游系统之间的通信相互依赖&a…...
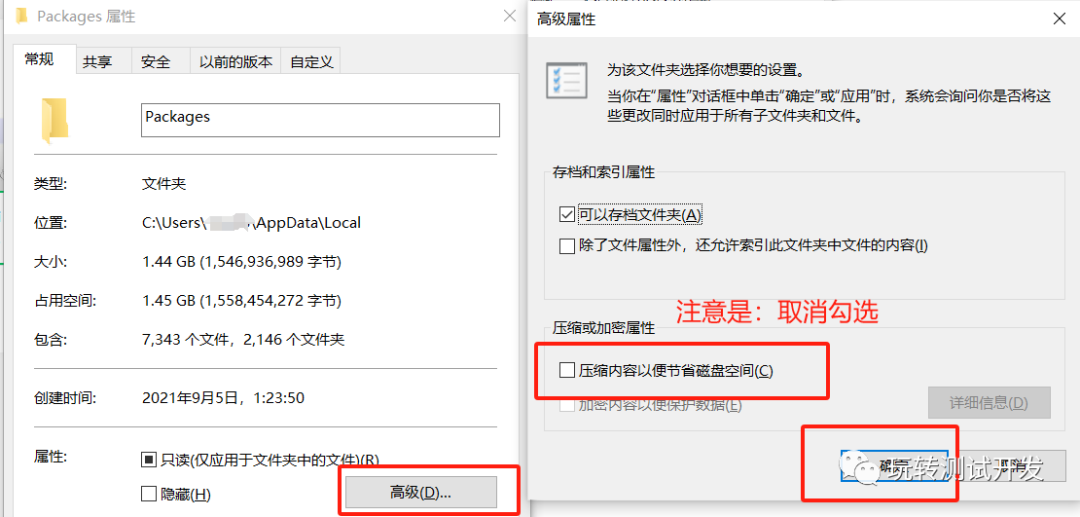
WSL安装异常:WslRegisterDistribution failed with error: 0xc03a001a
简介:如果文件夹右上角是否都有两个相对的蓝色箭头,在进行安装wsl时,设置就会抛出 Installing WslRegisterDistribution failed with error: 0xc03a001a的异常 历史攻略: 卸载WSL WSL:运行Linux文件 WSL࿱…...

【C语言 模拟实现strcmp函数】
C语言程序设计笔记---025 C语言之模拟实现strcmp函数1、介绍strcmp函数2、模拟实现strcmp函数3、结语 C语言之模拟实现strcmp函数 前言: 通过C语言字符串函数的知识,这篇将对strcmp函数进行深入学习底层原理的知识,并模拟实现对应功能。 /知…...

maven 依赖版本冲突异常
maven 依赖版本冲突异常 好巧不巧,前几天刚刚复习完 maven 的内容今天就碰到 maven 报错。 起因是这样的,项目马上快要上线了,在上线之前需要跑一些 audit 去检查项目是否安全(这里主要是 outdated 的依赖检查)。总体…...
11.5-LE Audio 笔记之Context Type)
蓝牙核心规范(V5.4)11.5-LE Audio 笔记之Context Type
专栏汇总网址:蓝牙篇之蓝牙核心规范学习笔记(V5.4)汇总_蓝牙核心规范中文版_心跳包的博客-CSDN博客 爬虫网站无德,任何非CSDN看到的这篇文章都是盗版网站,你也看不全。认准原始网址。!!! 蓝牙中的上下文类型(Context Type)是用于描述音频流当前使用情况或相关使用情…...
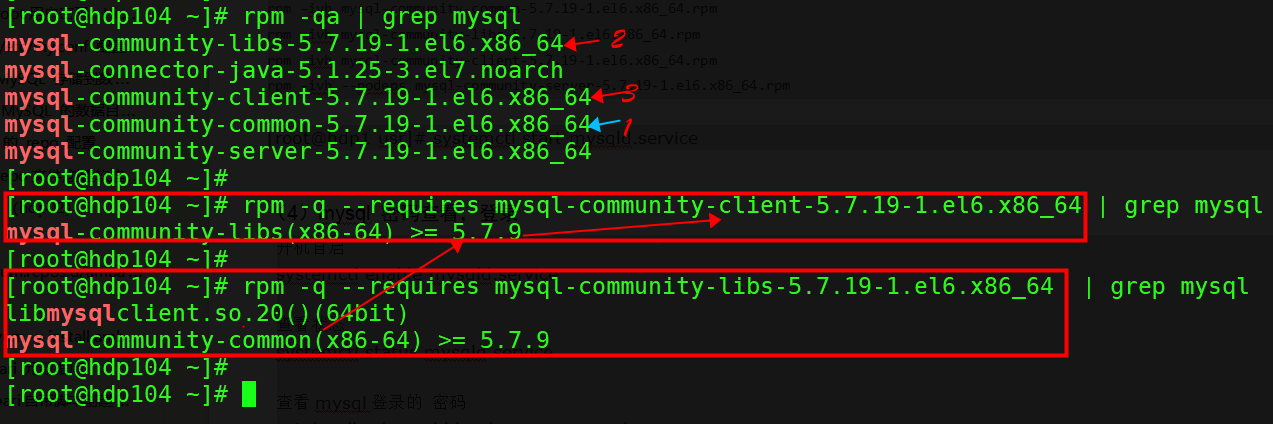
【Linux】RPM包使用详解
🍁 博主 "开着拖拉机回家"带您 Go to New World.✨🍁 🦄 个人主页——🎐开着拖拉机回家_大数据运维-CSDN博客 🎐✨🍁 🪁🍁 希望本文能够给您带来一定的帮助🌸文…...

勒索病毒最新变种.Elbie勒索病毒来袭,如何恢复受感染的数据?
引言: 网络犯罪正变得越来越隐秘和危险。其中,.Elbie勒索病毒作为数字犯罪的一部分,以其阴险和复杂性而备受关注。本文将带您深入探索.Elbie勒索病毒的工作原理和如何应对这一数字迷宫。如果受感染的数据确实有恢复的价值与必要性࿰…...

ArduPilot开源飞控之AP_Mission
ArduPilot开源飞控之AP_Mission 1. 源由2. AP_Mission类3 简令结构3.1 导航相关3.1.1 jump command3.1.2 condition delay command3.1.3 condition distance command3.1.4 condition yaw command3.1.5 change speed command3.1.6 nav guided command3.1.7 do VTOL transition3.…...

JVM111
JVM1 字节码与多语言混合编程 字节码 我们平时说的java字节码, 指的是用java语言编译成的字节码。准确的说任何能在jvm平台上执行的字节码格式都是一样的。所以应该统称为:jvm字节码。不同的编译器,可以编译出相同的字节码文件,字节码文件…...

排序篇(三)----交换排序
排序篇(三)----交换排序 1.冒泡排序 基本思想: 通过不断地比较相邻的元素,将较大的元素往后移动,从而实现排序的目的。 具体的步骤如下: 从待排序的数组中选择相邻的两个元素进行比较,如果前一个元素大于后一个元素&#…...

React antd Table点击下一页后selectedRows丢失之前页选择内容的问题
一、问题 使用了React antd 的<Table>标签,是这样记录选中的行id与行内容的: <TabledataSource{data.list}rowSelection{{selectedRowKeys: selectedIdsInSearchTab,onChange: this.onSelectChange,}} // 表格是否可复选,加 type: …...
11.4-LE Audio 笔记之音频模型)
蓝牙核心规范(V5.4)11.4-LE Audio 笔记之音频模型
专栏汇总网址:蓝牙篇之蓝牙核心规范学习笔记(V5.4)汇总_蓝牙核心规范中文版_心跳包的博客-CSDN博客 爬虫网站无德,任何非CSDN看到的这篇文章都是盗版网站,你也看不全。认准原始网址。!!! 从一开始,蓝牙低功耗(Bluetooth Low Energy,BLE)音频的开发就秉持着“以设…...

Spring Boot:利用JPA进行数据库的查删
目录标题 DAO 、Service 、 Controller 层控制器文件示例代码-单个查找查找成功示例代码-列表查找查找成功示例代码-删除删除成功 DAO 、Service 、 Controller 层 DAO 层负责数据库访问,它封装了对数据库的访问操作,例如查询、插入、更新和删除等。 Q…...

1711: 【穷举】满足条件的整数
题目描述 假设a、b、c均为整数(1<a,b,c<100),同时a<b,找出所有符合条件:a2 b2 n*c3的整数组。 按a从小到大的顺序输出所有满足条件的整数组(若a相同,则按b从小到大的顺序输出) 输入…...

【数据结构】堆的应用-----TopK问题
目录 一、前言 二、Top-k问题 💦解法一:暴力排序 💦解法二:建立N个数的堆 💦解法三:建立K个数的堆(最优解) 三、完整代码和视图 四、共勉 一、前言 在之前的文章中ÿ…...

QT之xml文件的读写
QT之xml文件的读写 简介用法举例 简介 QT的QDomDocument、QDomElement、QDomNode是Qt XML模块中的三个类,用于解析和操作XML文档。 1)QDomDocument类: QDomDocument类表示整个XML文档。它提供了解析XML文档的方法,如setContent(…...

C语言中的异常处理机制是什么?
C语言中的异常处理机制 C语言是一门强大而灵活的编程语言,它为程序员提供了广泛的控制权和自由度。然而,C语言本身并不提供像其他高级语言一样的内置异常处理机制,如Java中的try-catch或Python中的异常处理。因此,C语言程序员需要…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器
拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件: 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...

水泥厂自动化升级利器:Devicenet转Modbus rtu协议转换网关
在水泥厂的生产流程中,工业自动化网关起着至关重要的作用,尤其是JH-DVN-RTU疆鸿智能Devicenet转Modbus rtu协议转换网关,为水泥厂实现高效生产与精准控制提供了有力支持。 水泥厂设备众多,其中不少设备采用Devicenet协议。Devicen…...

ubuntu系统文件误删(/lib/x86_64-linux-gnu/libc.so.6)修复方案 [成功解决]
报错信息:libc.so.6: cannot open shared object file: No such file or directory: #ls, ln, sudo...命令都不能用 error while loading shared libraries: libc.so.6: cannot open shared object file: No such file or directory重启后报错信息&…...

何谓AI编程【02】AI编程官网以优雅草星云智控为例建设实践-完善顶部-建立各项子页-调整排版-优雅草卓伊凡
何谓AI编程【02】AI编程官网以优雅草星云智控为例建设实践-完善顶部-建立各项子页-调整排版-优雅草卓伊凡 背景 我们以建设星云智控官网来做AI编程实践,很多人以为AI已经强大到不需要程序员了,其实不是,AI更加需要程序员,普通人…...
