机器学习7:逻辑回归

一、说明
逻辑回归模型是处理分类问题的最常见机器学习模型之一。二项式逻辑回归只是逻辑回归模型的一种类型。它指的是两个变量的分类,其中概率用于确定二元结果,因此“二项式”中的“bi”。结果为真或假 — 0 或 1。
二项式逻辑回归的一个例子是预测人群中 COVID-19 的可能性。一个人要么感染了COVID-19,要么没有,必须建立一个阈值以尽可能准确地区分这些结果。
二、sigmoid函数
这些预测不适合一条线,就像线性回归模型一样。相反,逻辑回归模型拟合到右侧所示的 sigmoid 函数。
对于每个 x,生成的 y 值表示结果为 True 的概率。在 COVID-19 示例中,这表示医生对某人感染病毒的信心。在右图中,阴性结果为蓝色,阳性结果为红色。
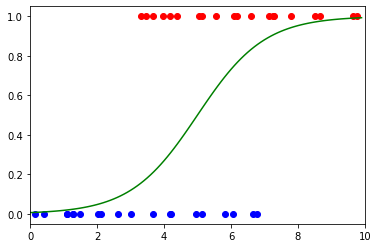
图片来源:作者
三、过程
要进行二项式逻辑回归,我们需要做各种事情:
- 创建训练数据集。
- 使用 PyTorch 创建我们的模型。
- 将我们的数据拟合到模型中。
逻辑回归问题的第一步是创建训练数据集。首先,我们应该设置一个种子来确保我们的随机数据的可重复性。
import numpy as np
import matplotlib.pyplot as plt
import torch
import torch.nn as nn
from torch.nn import Lineartorch.manual_seed(42) # set a random seed我们必须使用 PyTorch 的线性模型,因为我们正在处理一个输入 x 和一个输出 y。因此,我们的模型是线性的。为此,我们将使用 PyTorch 的函数:Linear
model = Linear(in_features=1, out_features=1) # use a linear model接下来,我们必须生成蓝色 X 和红色 X 数据,确保将它们从行向量重塑为列向量。蓝色的在 0 到 7 之间,红色的在 7 到 10 之间。对于 y 值,蓝点表示 COVID-19 测试阴性,因此它们都将是
- 对于红点,它们代表 COVID-19 测试呈阳性,因此它们将为 1。下面是代码及其输出:
blue_x = (torch.rand(20) * 7).reshape(-1,1) # random floats between 0 and 7
blue_y = torch.zeros(20).reshape(-1,1)red_x = (torch.rand(20) * 7+3).reshape(-1,1) # random floats between 3 and 10
red_y = torch.ones(20).reshape(-1,1)X = torch.vstack([blue_x, red_x]) # matrix of x values
Y = torch.vstack([blue_y, red_y]) # matrix of y values现在,我们的代码应如下所示:
import numpy as np
import matplotlib.pyplot as plt
import torch
import torch.nn as nn
from torch.nn import Lineartorch.manual_seed(42) # set a random seedmodel = Linear(in_features=1, out_features=1) # use a linear modelblue_x = (torch.rand(20) * 7).reshape(-1,1) # random floats between 0 and 7
blue_y = torch.zeros(20).reshape(-1,1)red_x = (torch.rand(20) * 7+3).reshape(-1,1) # random floats between 3 and 10
red_y = torch.ones(20).reshape(-1,1)X = torch.vstack([blue_x, red_x]) # matrix of x values
Y = torch.vstack([blue_y, red_y]) # matrix of y values四、优化
我们将使用梯度下降过程来优化 S 形函数的损失。损失是根据函数拟合数据的优度计算的,数据由 S 形曲线的斜率和截距控制。我们需要梯度下降来找到最佳斜率和截距。
我们还将使用二进制交叉熵(BCE)作为我们的损失函数,或对数损失函数。对于一般的逻辑回归,不包含对数的损失函数将不起作用。
为了实现BCE作为我们的损失函数,我们将它设置为我们的标准,并将随机梯度下降作为我们优化它的手段。由于这是我们将要优化的函数,我们需要传入模型参数和学习率。
epochs = 2000 # run 2000 iterations
criterion = nn.BCELoss() # implement binary cross entropy loss functionoptimizer = torch.optim.SGD(model.parameters(), lr = .1) # stochastic gradient descent现在,我们准备开始梯度下降以优化我们的损失。我们必须将梯度归零,通过将我们的数据插入 sigmoid 函数来找到 y-hat 值,计算损失,并找到损失函数的梯度。然后,我们必须迈出一步,确保存储我们的新斜率并为下一次迭代进行拦截。
optimizer.zero_grad()
Yhat = torch.sigmoid(model(X))
loss = criterion(Yhat,Y)
loss.backward()
optimizer.step() 五、收尾
为了找到最佳斜率和截距,我们本质上是在训练我们的模型。我们必须对多次迭代或纪元应用梯度下降。在此示例中,我们将使用 2,000 个纪元进行演示。
epochs = 2000 # run 2000 iterations
criterion = nn.BCELoss() # implement binary cross entropy loss functionoptimizer = torch.optim.SGD(model.parameters(), lr = .1) # stochastic gradient descentfor i in range(epochs):optimizer.zero_grad()Yhat = torch.sigmoid(model(X))loss = criterion(Yhat,Y)loss.backward()optimizer.step()print(f"epoch: {i+1}")print(f"loss: {loss: .5f}")print(f"slope: {model.weight.item(): .5f}")print(f"intercept: {model.bias.item(): .5f}")print()将所有代码片段放在一起,我们应该得到以下代码:
import numpy as np
import matplotlib.pyplot as plt
import torch
import torch.nn as nn
from torch.nn import Lineartorch.manual_seed(42) # set a random seedmodel = Linear(in_features=1, out_features=1) # use a linear modelblue_x = (torch.rand(20) * 7).reshape(-1,1) # random floats between 0 and 7
blue_y = torch.zeros(20).reshape(-1,1)red_x = (torch.rand(20) * 7+3).reshape(-1,1) # random floats between 3 and 10
red_y = torch.ones(20).reshape(-1,1)X = torch.vstack([blue_x, red_x]) # matrix of x values
Y = torch.vstack([blue_y, red_y]) # matrix of y valuesepochs = 2000 # run 2000 iterations
criterion = nn.BCELoss() # implement binary cross entropy loss functionoptimizer = torch.optim.SGD(model.parameters(), lr = .1) # stochastic gradient descentfor i in range(epochs):optimizer.zero_grad()Yhat = torch.sigmoid(model(X))loss = criterion(Yhat,Y)loss.backward()optimizer.step()print(f"epoch: {i+1}")print(f"loss: {loss: .5f}")print(f"slope: {model.weight.item(): .5f}")print(f"intercept: {model.bias.item(): .5f}")print()
两千个时期后的最终输出:epoch: 2000
loss: 0.53861
slope: 0.61276
intercept: -3.17314两千个时期后的最终输出:
epoch: 2000
loss: 0.53861
slope: 0.61276
intercept: -3.17314 六、可视化
最后,我们可以将数据与 sigmoid 函数一起绘制,以获得以下可视化效果:
x = np.arange(0,10,.1)
y = model.weight.item()*x + model.bias.item()plt.plot(x, 1/(1 + np.exp(-y)), color="green")plt.xlim(0,10)
plt.scatter(blue_x, blue_y, color="blue")
plt.scatter(red_x, red_y, color="red")plt.show()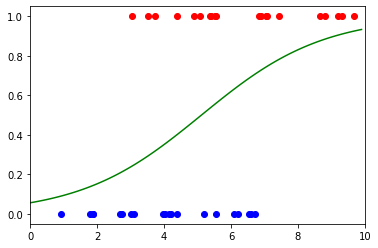
图片来源:作者
七、局限性
二元分类的最大问题之一是需要阈值。在逻辑回归的情况下,此阈值应为 x 值,其中 y 为 50%。我们试图回答的问题是将阈值放在哪里?
在 COVID-19 测试的情况下,原始示例说明了这种困境。如果我们将阈值设置为 x=5,我们可以清楚地看到应该是红色的蓝点和应该是蓝色的红点。
悬垂的红点称为误报,即模型错误地预测正类的区域。悬垂的蓝点称为假阴性 - 模型错误地预测负类的区域。
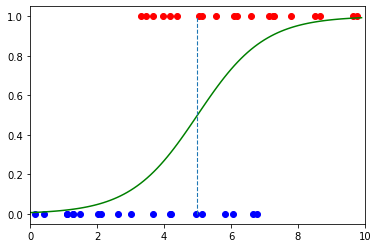
八、结论
成功的二项式逻辑回归模型将减少假阴性的数量,因为这些假阴性通常会导致最大的危险。患有COVID-19但检测呈阴性对他人的健康和安全构成严重风险。
通过对可用数据使用二项式逻辑回归,我们可以确定放置阈值的最佳位置,从而有助于减少不确定性并做出更明智的决策。
相关文章:

机器学习7:逻辑回归
一、说明 逻辑回归模型是处理分类问题的最常见机器学习模型之一。二项式逻辑回归只是逻辑回归模型的一种类型。它指的是两个变量的分类,其中概率用于确定二元结果,因此“二项式”中的“bi”。结果为真或假 — 0 或 1。 二项式逻辑回归的一个例子是预测人…...

生活小记-纸张尺寸
A系列纸张: A0:841 x 1189 毫米A1:594 x 841 毫米A2:420 x 594 毫米A3:297 x 420 毫米A4:210 x 297 毫米A5:148 x 210 毫米A6:105 x 148 毫米A7:74 x 105 毫米A8…...
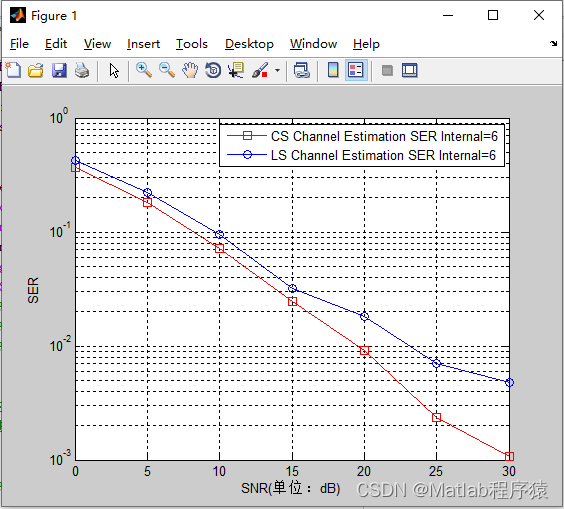
【MATLAB源码-第41期】基于压缩感知算法的OFDM系统信道估计和LS算法对比仿真。
操作环境: MATLAB 2013b 1、算法描述 压缩感知(Compressed Sensing, CS)是一种从稀疏或可压缩信号中重构完整信号的数学理论和技术。下面详细介绍压缩感知和它在OFDM信道估计中的应用。 1. 压缩感知基本概念 在传统采样理论中࿰…...

优思学院|六西格玛将烹饪和美味提升至极致
最近,我们曾提到一个美国男子如何利用六西格玛来控制糖尿病。这表明六西格玛逐渐被认为是一个不仅可以在工作场所之外使用,尤其不仅限于制造业的系统。 六西格玛的核心理念是改进过程的质量,从而改善最终结果。如果你做了晚餐或尝试了一道新…...

git stash
git stash 是 Git 中一个非常有用的命令,用于临时保存当前工作目录中的修改,以便你可以切换到其他分支或处理其他任务而不丢失你的修改。它的主要用途是: 保存未提交的修改:你可以使用 git stash 命令将未提交的修改(包…...

Flink Data Source
Flink Data Source 一、内置 Data Source Flink Data Source 用于定义 Flink 程序的数据来源,Flink 官方提供了多种数据获取方法,用于帮助开发者简单快速地构建输入流,具体如下: 1.1 基于文件构建 1. readTextFile(path):按照 TextInputFormat 格式读取文本文件,并将…...
怒刷LeetCode的第23天(Java版)
目录 第一题 题目来源 题目内容 解决方法 方法一:贪心算法 方法二:动态规划 方法三:回溯算法 方法四:并查集 第二题 题目来源 题目内容 解决方法 方法一:排序和遍历 方法二:扫描线算法 方法…...

Golang 中的调试技巧
掌握有效的策略和工具,实现顺畅的开发 调试是每位开发人员都必须掌握的关键技能。它是识别、隔离和解决代码库中问题的过程。在 Golang 的世界中,掌握有效的调试技巧可以显著提升您的开发工作流程,并帮助您创建更可靠和健壮的应用程序。在本…...

linux 监控内存利用率
监控内存利用率 使用free来分析CPU使用信息 #!/bin/bashDATE$(date %F" "%H:%M)IP$(ifconfig eth0 |awk -F [ :] /inet addr/{print $4}) MAIL"examplemail.com"TOTAL$(free -m |awk /Mem/{print $2})USE$(free -m |awk /Mem/{print $3-$6-$7})FREE$(($TO…...
43 验证二叉搜索树
验证二叉搜索树 理解题意:验证搜索二叉树:中序遍历是升序题解1 递归(学习学习!)题解2 中序遍历(保持升序) 给你一个二叉树的根节点 root ,判断其是否是一个 有效的二叉搜索树。 有…...
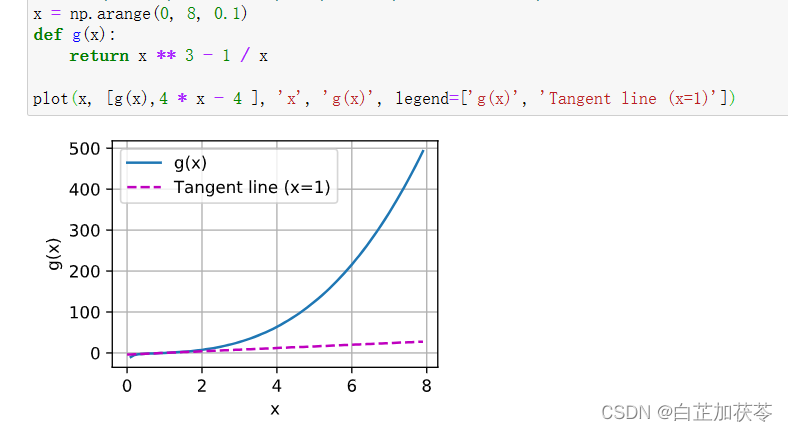
深度学习笔记之微积分及绘图
深度学习笔记之微积分及绘图 学习资料来源:微积分 %matplotlib inline from matplotlib_inline import backend_inline from mxnet import np, npx from d2l import mxnet as d2lnpx.set_np()def f(x):return 3 * x ** 2 - 4 * xdef numerical_lim(f, x, h):retur…...
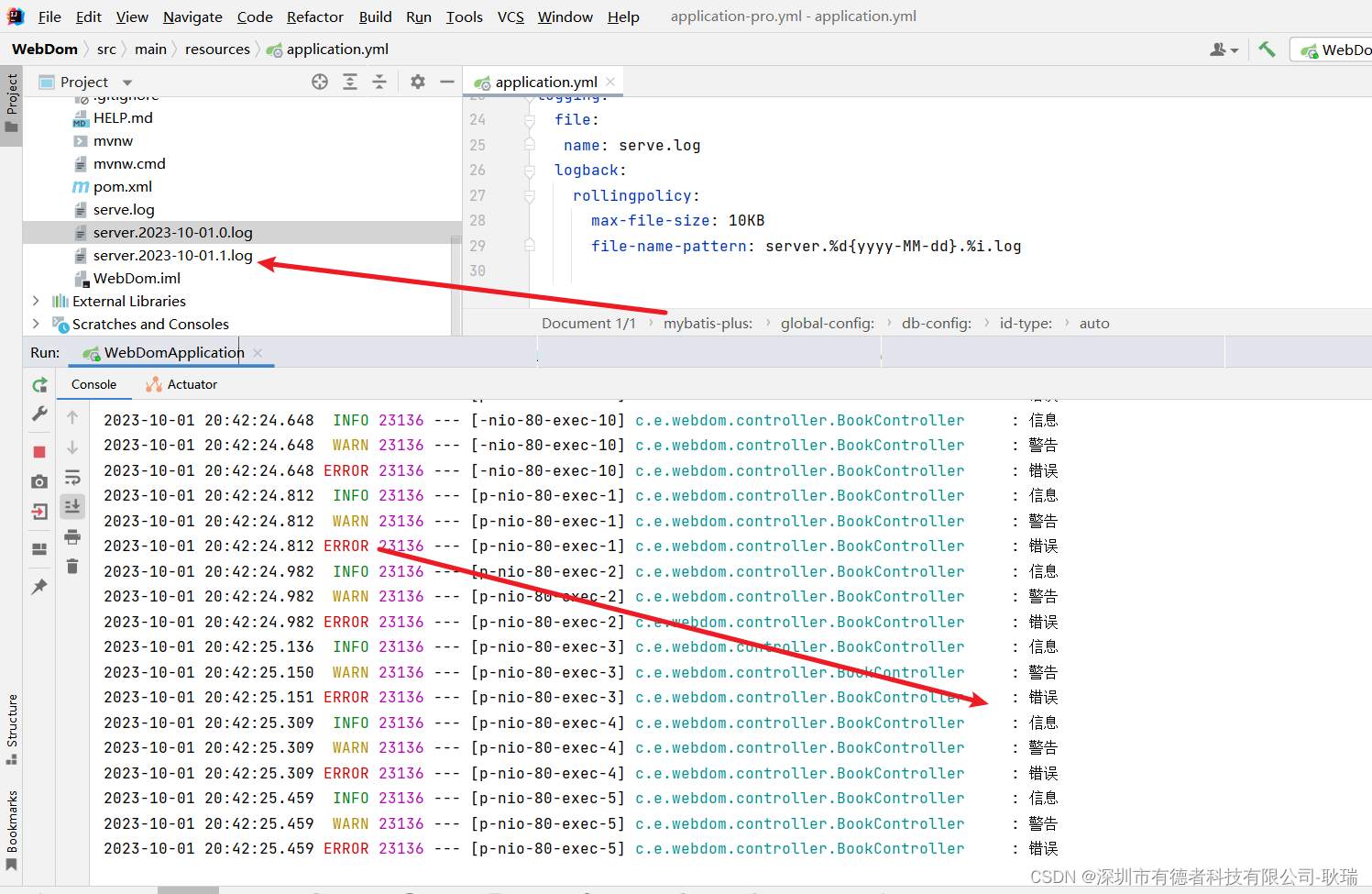
java Spring Boot按日期 限制大小分文件记录日志
上文 java Spring Boot 将日志写入文件中记录 中 我们实现另一个将控制台日志写入到 项目本地文件的效果 但是 这里有个问题 比如 我项目是个大体量的企业项目 每天会有一百万用户访问 那我每天的日志都记载同一个文件上 那不跟没记没什么区别吗? 东西怎么找&#x…...

CSS 语法
CSS 实例 CSS 规则由两个主要的部分构成:选择器,以及一条或多条声明: 选择器通常是您需要改变样式的 HTML 元素。 每条声明由一个属性和一个值组成。 属性(property)是您希望设置的样式属性(style attribute&#x…...
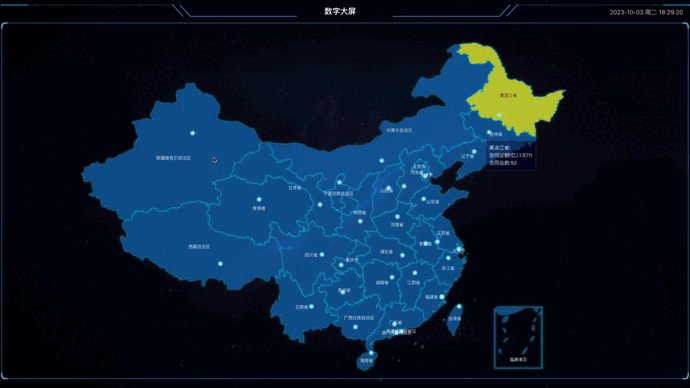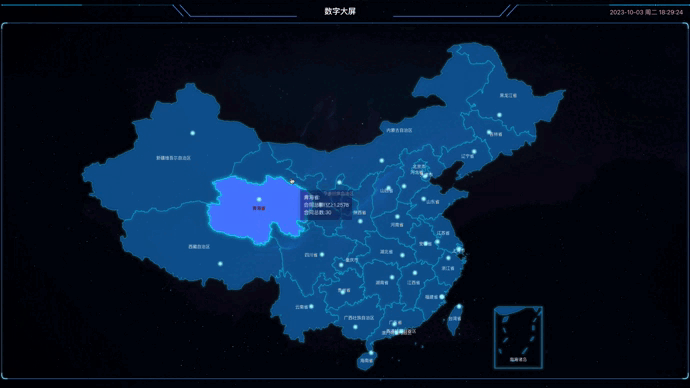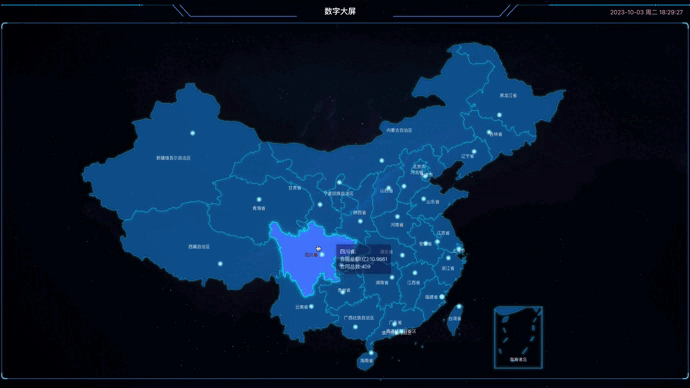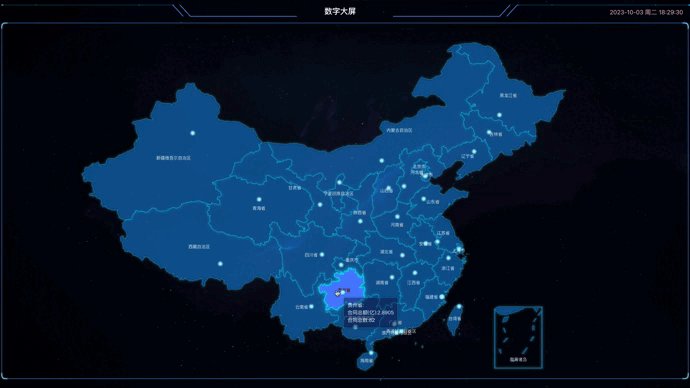
Vue3+TS+ECharts5实现中国地图数据信息显示
1.引言 最近在做一个管理系统,主要技术栈使用的是Vue3TSViteElementPlus,主要参考项目是yudao-ui-admin-vue3,其中用到ECharts5做数字大屏,展示中国地图相关信息,以此基础做一个分享,写下这篇文章。 &quo…...

PowerShell 内网不能直接安装SqlServer模块的处理办法
PowerShell 内网不能直接安装SqlServer模块的处理办法 文章目录 下载sqlserver module安装sqlserver module导入和验证sqlserver 模块推荐阅读 下载sqlserver module 首先先将sqlserver.nupkg下载到本地,我是放到了C:\windows\system32目录下。 PowerShell Galler…...

Git使用【下】
欢迎来到Cefler的博客😁 🕌博客主页:那个传说中的man的主页 🏠个人专栏:题目解析 🌎推荐文章:题目大解析(3) 目录 👉🏻标签管理理解标签标签运用 …...
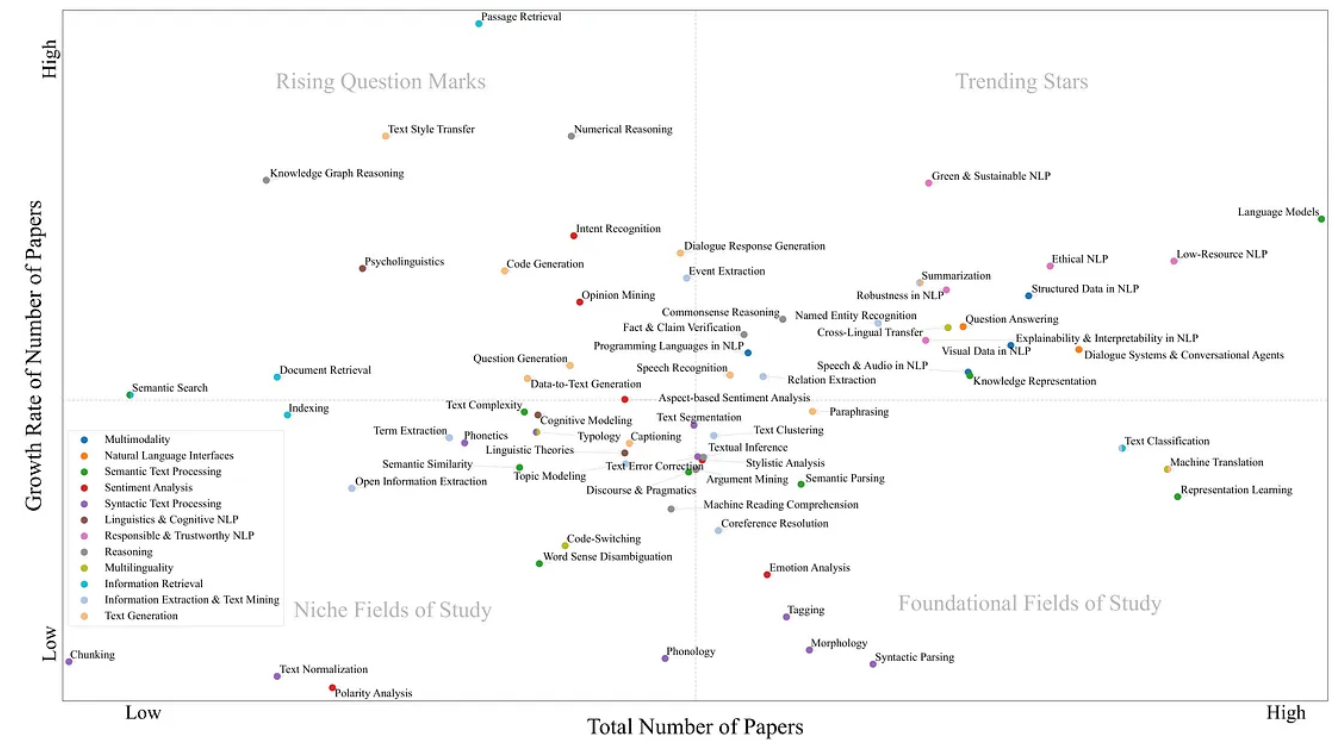
自然语言处理的分类
动动发财的小手,点个赞吧! 简介 作为理解、生成和处理自然语言文本的有效方法,自然语言处理(NLP)的研究近年来呈现出快速传播和广泛采用。鉴于 NLP 的快速发展,获得该领域的概述并对其进行维护是很困难的。…...
Flutter笔记:手写并发布一个人机滑动验证码插件
Flutter笔记 手写一个人机滑块验证码 作者:李俊才 (jcLee95):https://blog.csdn.net/qq_28550263 邮箱 :291148484163.com 本文地址:https://blog.csdn.net/qq_28550263/article/details/133529459 写 Flut…...
RabbitMQ安装与简单使用
安装 下载资源 可以访问官网查看下载信息rabbitmq官网 选择合适的版本,注意:rabbitmq需要下载一个Erlang才能使用 我自己是在一下两个连接中下载的 rabbitmq 3.8.8 erlang 21.3.8.15 需要下载其他版本的同学注意erlang版本是否匹配,可以访…...

不做静态化,当部署到服务器上的项目刷新出现404【已解决】
当线上项目刷新出现404页面解决方法: 在nginx配置里加入这样一段代码 try_files $uri $uri/ /index.html; 它的作用是尝试按照给定的顺序访问文件 变量解释 try_files 固定语法 $uri 指代home文件(ip地址后面的路径,假如是127.0.0.1/index/a.png&…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...
