机器学习(监督学习)笔记
目录
- 总览
- 笔记内容
- 线性回归
- 梯度下降
- 特征缩放
- 多输出线性回归
- 逻辑回归
- 二分类与逻辑回归
- 分类任务的性能指标(召回率,精度,F1分数等)
- 支持向量机SVM
- K近邻
- 朴素贝叶斯分类器
- 朴素贝叶斯分类器进阶
- 多分类逻辑回归
- 二分类神经网络
- 多分类神经网络
- 代码部分
- 实验一代码(批梯度,小批度,随机批度下降手撸)
- 实验二 线性回归代码手撸(批梯度)
- 实验三 线性回归代码手撸(随机批度)
- 实验四 线性回归代码手撸(小批度)
- 实验五 特征缩放手撸(标准化,归一化)
- 实验八 线性回归二分类
- 实验九 均方差(MSE)-逻辑回归模型
- 实验九 均方差(MSE)-逻辑回归模型3D版本
- 实验十 交叉熵-逻辑回归模型(R,P,F1)
- 实验十一 scikit-learn SVM
- 实验十二 SVM(错误率随C值变化)
- 实验十三 K交叉验证-SVM
- 实验十四 K近邻(K变化)-K交叉验证
- 实验十五 宏F1值,马修斯相关系数
- 实验十六 高斯朴素贝叶斯分类器
- 实验十七 多分类逻辑回归
- 二分类逻辑回归的不足
- 二分类逻辑回归强化
- 实验十八 二分类神经网络
- 实验十九 多分类神经网络
- 资源地址
- 项目地址
- 总结
总览
本文是机器学习的学习笔记(监督学习部分),全手撸了课程这部分的代码。
教材是《机器学习原理与实践》微课版,作者陈喆。
笔记内容
线性回归

梯度下降






特征缩放

多输出线性回归



逻辑回归
二分类与逻辑回归





分类任务的性能指标(召回率,精度,F1分数等)



支持向量机SVM






K近邻


朴素贝叶斯分类器

朴素贝叶斯分类器进阶



多分类逻辑回归





二分类神经网络







多分类神经网络


代码部分
实验一代码(批梯度,小批度,随机批度下降手撸)
# 实验2-1
# 批梯度下降
import pandas as pd
import numpy as np
import random as rd
import matplotlib.pyplot as plt
# load dataset
df = pd.read_csv('temperature_dataset.csv')
data = np.array(df)
y0 = np.array([i[0] for i in data]) # 第一列作为样本标注
y14 = np.array([i[1:] for i in data])#2-5 作为四维输出特征
xuexi = 0.0001 # 学习率
ep = 20
epoch = [ep] # 遍历次数
m = np.size(data,0) # 获取样本长度 m
alls = [i for i in range(m)]
trainsyo = [] # 训练集标注
testyo = [] # 测试集标注
trainsy14 = [] # 训练集输入特征
testy14 = [] # 测试集输入特征
tra = int(m * 0.8) # 训练集长度
tes = m - tra # 测试集长度
for i in range(tra): # 获取训练集a = rd.choice(alls) # 从alls中随机选取一个trainsyo.append(y0[a]) # 增加训练集标注trainsy14.append(y14[a])# 增加训练集输入特征alls.remove(a)
trainsy14 = np.array(trainsy14) # 训练集list转变array
trainsyo = np.array(trainsyo) # 训练集list转变array
for a in alls: # 获取测试集
# global y0
# global y14testyo.append(y0[a])# 增加测试集标注testy14.append(y14[a]) # 增加测试集输入特征
w = np.array([rd.random() for i in range(4)]) # 初次随机获取权重w
# print(w)
b = [rd.random()] # 初次随机获取偏差b
RMSE = [] # 均方根误差
RMSE2 = [] # 训练集
while(epoch[0]): # 开始遍历epoch[0] -= 1 # 设置的超参数epoch -1e =np.dot(testy14,w.transpose()) + b[0] - testyoRMSE.append((np.dot(e,e.transpose())/tes)**0.5)e = np.dot(trainsy14,w.transpose()) + b[0] - trainsyo # n*1RMSE2.append((np.dot(e,e.transpose())/tra)**0.5)b[0] -= 2*xuexi*np.dot(np.ones(tra),e)/traw -= 2*xuexi*np.dot(e.transpose(),trainsy14)/tra
# 绘图部分
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
x = [i+1 for i in range(ep)] # 设置x坐标
print(min(RMSE),min(RMSE2))
ymax = max(RMSE) + 1
plt.xlabel('epoch') # 设置x坐标名称
plt.ylabel('RMSE') # 设置y坐标名称
plt.title('训练情况') # 设置标题
plt.plot(x,RMSE,color='r',marker='o',linestyle='dashed')
# plt.plot(x,RMSE,color='r') # 设置绘图的基本参数
plt.axis([0,ep+ 1,0,ymax]) # 设置xy的取值范围
plt.show() # 展示图片实验二 线性回归代码手撸(批梯度)
# 2-2
import pandas as pd
import numpy as np
import random as rd
import matplotlib.pyplot as plt
# load dataset
df = pd.read_csv('temperature_dataset.csv')
data = np.array(df)
y0 = np.array([i[0] for i in data]) # 第一列作为样本标注
y14 = np.array([i[3] for i in data])# 选第三维作为输入特征
xuexi = 0.0001 # 学习率
ep = 20
epoch = [ep] # 遍历次数
m = np.size(data,0) # 获取样本长度 m
alls = [i for i in range(m)]
trainsyo = [] # 训练集标注
testyo = [] # 测试集标注
trainsy14 = [] # 训练集输入特征
testy14 = [] # 测试集输入特征
tra = int(m * 0.8) # 训练集长度
tes = m - tra # 测试集长度
allw = [] # 训练过程中的全部的w
allb = [] # 训练过程中的全部的b
for i in range(tra): # 获取训练集a = rd.choice(alls) # 从alls中随机选取一个trainsyo.append(y0[a]) # 增加训练集标注trainsy14.append(y14[a])# 增加训练集输入特征alls.remove(a)
trainsy14 = np.array(trainsy14) # 训练集list转变array
trainsyo = np.array(trainsyo) # 训练集list转变array
for a in alls: # 获取测试集
# global y0
# global y14testyo.append(y0[a])# 增加测试集标注testy14.append(y14[a]) # 增加测试集输入特征
w = np.array([rd.random() for i in range(1)]) # 初次随机获取权重w
# print(w)
b = [rd.random()] # 初次随机获取偏差b
RMSE = [] # 均方根误差
while(epoch[0]): # 开始遍历epoch[0] -= 1 # 设置的超参数epoch -1newb = 0 # 求解的b的值newW = int() # 求解的w的值for i in range(tra): # 遍历全部的训练集a = np.dot(w,trainsy14[i].transpose()) + b[0] - trainsyo[i] # 计算(W*xT + b - y )newb += float(a) # 累加if type(newW) == int: newW = trainsy14[i].transpose()*float(a) # 初次赋值else:newW += trainsy14[i].transpose()*float(a) # 累加ww -= xuexi*newW * (2/tra) # 更新wb[0] -= xuexi*newb *2 / tra # 更新ballw.append(w[0])allb.append(b[0])
yall = []
xs= [-5,-3,--1,0,1,3,5] # x 轴模板
xall = [xs for i in range(ep)]
ymax = 0
ymin = 30
for i in range(ep):yall.append([allw[i]*t + allb[i] for t in xs])ymax = max(ymax,max(yall[i]))ymin = min(ymin,min(yall[i]))
#绘图部分
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
x = [i+1 for i in range(ep)] # 设置x坐标
plt.xlabel('x') # 设置x坐标名称
plt.ylabel('y') # 设置y坐标名称
plt.title('拟合直线变化') # 设置标题
plots = []
for i in range(ep):c='r'if i == 0:c = 'b'elif i == ep -1:c = 'k'p, = plt.plot(xall[i],yall[i],color=c,marker='o',linestyle='dashed')plots.append(p)
# plt.plot(x,RMSE,color='r') # 设置绘图的基本参数
plt.legend((plots[0],plots[-1]),['start','end'])
plt.axis([-6,6,ymin-1,ymax+1]) # 设置xy的取值范围
plt.show() # 展示图片
实验三 线性回归代码手撸(随机批度)
# 2-3
# 随机梯度下降
import pandas as pd
import numpy as np
import random as rd
import matplotlib.pyplot as plt
# load dataset
np.random.seed(100)
rng = np.random.default_rng()
df = pd.read_csv('temperature_dataset.csv')
data = np.array(df)
y0 = np.array([i[0] for i in data]) # 第一列作为样本标注
y14 = np.array([i[1:] for i in data])#2-5 作为四维输出特征
xuexi = 0.0001 # 学习率
ep = 200
epoch = [ep] # 遍历次数
m = np.size(data,0) # 获取样本长度 m
alls = [i for i in range(m)]
trainsyo = [] # 训练集标注
testyo = [] # 测试集标注
trainsy14 = [] # 训练集输入特征
testy14 = [] # 测试集输入特征
tra = int(m * 0.8) # 训练集长度
tes = m - tra # 测试集长度
for i in range(tra): # 获取训练集a = rd.choice(alls) # 从alls中随机选取一个trainsyo.append(y0[a]) # 增加训练集标注trainsy14.append(y14[a])# 增加训练集输入特征alls.remove(a)
trainsy14 = np.array(trainsy14) # 训练集list转变array
trainsyo = np.array(trainsyo) # 训练集list转变array
for a in alls: # 获取测试集
# global y0
# global y14testyo.append(y0[a])# 增加测试集标注testy14.append(y14[a]) # 增加测试集输入特征
w = np.array([rd.random() for i in range(4)]) # 初次随机获取权重w
# print(w)
b = [rd.random()] # 初次随机获取偏差b
RMSE = [] # 均方根误差
while(epoch[0]): # 开始遍历epoch[0] -= 1 # 设置的超参数epoch -1newtra = [i for i in range(tra)]rd.shuffle(newtra)i = rd.choice(newtra)a = np.dot(w,trainsy14[i].transpose()) + b[0] - trainsyo[i] # 计算(W*xT + b - y )b[0] -= 2*xuexi*aw -= 2*xuexi*trainsy14[i].transpose()*a # 初次赋值y = 0 # 中间变量用于存储RMSE每一轮的for i in range(tes): # y += (np.dot(w,testy14[i].transpose()) + b[0] - testyo[i])**2 # 计算均方根误差,并累加 RMSE.append((y/tes)**0.5)
# 绘图部分
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
x = [i+1 for i in range(ep)] # 设置x坐标
print(min(RMSE))
ymax = max(RMSE) + 1
plt.xlabel('epoch') # 设置x坐标名称
plt.ylabel('RMSE') # 设置y坐标名称
plt.title('训练情况') # 设置标题
plt.plot(x,RMSE,color='r',marker='o',linestyle='dashed')
# plt.plot(x,RMSE,color='r') # 设置绘图的基本参数
plt.axis([0,ep+ 1,0,ymax]) # 设置xy的取值范围
plt.show() # 展示图片实验四 线性回归代码手撸(小批度)
# 2-4
# 小批梯度下降
import pandas as pd
import numpy as np
import random as rd
import matplotlib.pyplot as plt
# load dataset
df = pd.read_csv('temperature_dataset.csv')
data = np.array(df)
y0 = np.array([i[0] for i in data]) # 第一列作为样本标注
y14 = np.array([i[1:] for i in data])#2-5 作为四维输出特征
xuexi = 0.0001 # 学习率
batch = 30 # 设置批长度
ep = 20 # 设置遍历次数
epoch = [ep] # 遍历次数
m = np.size(data,0) # 获取样本长度 m
alls = [i for i in range(m)]
trainsyo = [] # 训练集标注
testyo = [] # 测试集标注
trainsy14 = [] # 训练集输入特征
testy14 = [] # 测试集输入特征
tra = int(m * 0.8) # 训练集长度
tes = m - tra # 测试集长度
for i in range(tra): # 获取训练集a = rd.choice(alls) # 从alls中随机选取一个trainsyo.append(y0[a]) # 增加训练集标注trainsy14.append(y14[a])# 增加训练集输入特征alls.remove(a)
trainsy14 = np.array(trainsy14) # 训练集list转变array
trainsyo = np.array(trainsyo) # 训练集list转变array
for a in alls: # 获取测试集
# global y0
# global y14testyo.append(y0[a])# 增加测试集标注testy14.append(y14[a]) # 增加测试集输入特征
w = np.array([rd.random() for i in range(4)]) # 初次随机获取权重w
# print(w)
b = [rd.random()] # 初次随机获取偏差b
RMSE2 = []
RMSE = [] # 均方根误差
while(epoch[0]): # 开始遍历epoch[0] -= 1 # 设置的超参数epoch -1if not batch:breaktimes = tra // batchif tra % batch:times += 1for _ in range(times):starts = _*batchends = (_+1)*batchif (_+1)*batch >= tra:ends = trabatch = tra%batchif(not batch):breake =np.dot(testy14,w.transpose()) + b[0] - testyoRMSE.append((np.dot(e,e.transpose())/tes)**0.5)e = np.dot(trainsy14[starts:ends],w.transpose()) + b[0] - trainsyo[starts:ends] # n*1RMSE2.append((np.dot(e,e.transpose())/batch)**0.5)b[0] -= 2*xuexi*np.dot(np.ones(batch),e)/batchw -= 2*xuexi*np.dot(e.transpose(),trainsy14[starts:ends])/batch
# 绘图部分
print(min(RMSE))
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
x = [i+1 for i in range(20)] # 设置x坐标
RMSE = RMSE[:20]
ymax = max(RMSE[:20]) + 1
plt.xlabel('epoch') # 设置x坐标名称
plt.ylabel('RMSE') # 设置y坐标名称
plt.title('训练情况') # 设置标题
plt.plot(x,RMSE,color='r',marker='o',linestyle='dashed')
# plt.plot(x,RMSE,color='r') # 设置绘图的基本参数
plt.axis([-2,len(RMSE)+ 6,0,ymax+3]) # 设置xy的取值范围
plt.show() # 展示图片
实验五 特征缩放手撸(标准化,归一化)
#2-5
# 各种标准化
import pandas as pd
import numpy as np
import random as rd
import matplotlib.pyplot as plt
# load dataset
df = pd.read_csv('temperature_dataset.csv')
data = np.array(df)
y0 = np.array([i[0] for i in data]) # 第一列作为样本标注
y14 = np.array([i[1:] for i in data])#2-5 作为四维输出特征
# 标准化
# mean = np.mean(y14,0) # 平均值
# stds = np.std(y14,0,ddof=1)
# y14 = (y14-mean)/stds
# 最小最大归一化
# maxs = np.amax(y14,0)
# mins = np.amin(y14,0)
# y14 = (y14 - mins)/(maxs-mins)
# 均值归一化
mean = np.mean(y14,0) # 平均值
maxs = np.amax(y14,0)
mins = np.amin(y14,0)
y14 = (y14-mean)/(maxs - mins)
xuexi = 0.1 # 学习率
ep = 2000
epoch = [ep] # 遍历次数
m = np.size(data,0) # 获取样本长度 m
alls = [i for i in range(m)]
trainsyo = [] # 训练集标注
testyo = [] # 测试集标注
trainsy14 = [] # 训练集输入特征
testy14 = [] # 测试集输入特征
tra = int(m * 0.8) # 训练集长度
tes = m - tra # 测试集长度
for i in range(tra): # 获取训练集a = rd.choice(alls) # 从alls中随机选取一个trainsyo.append(y0[a]) # 增加训练集标注trainsy14.append(y14[a])# 增加训练集输入特征alls.remove(a)
trainsy14 = np.array(trainsy14) # 训练集list转变array
trainsyo = np.array(trainsyo) # 训练集list转变array
for a in alls: # 获取测试集testyo.append(y0[a])# 增加测试集标注testy14.append(y14[a]) # 增加测试集输入特征
# w = np.array([rd.random() for i in range(4)]) # 初次随机获取权重w
w =np.array([0.,0.,0.,0.])
# print(w)
# b = [rd.random()] # 初次随机获取偏差b
b = [0.]
RMSE = [] # 均方根误差
RMSE2 = [] # 训练集均方根误差
while(epoch[0]): # 开始遍历epoch[0] -= 1 # 设置的超参数epoch -1e =np.dot(testy14,w.transpose()) + b[0] - testyoRMSE.append((np.dot(e,e.transpose())/tes)**0.5)e = np.dot(trainsy14,w.transpose()) + b[0] - trainsyo # n*1RMSE2.append((np.dot(e,e.transpose())/tra)**0.5)b[0] -= 2*xuexi*np.dot(np.ones(tra),e)/traw -= 2*xuexi*np.dot(e.transpose(),trainsy14)/tra
# 绘图部分
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
x = [i+1 for i in range(ep)] # 设置x坐标
print(min(RMSE),min(RMSE2))
ymax = max(RMSE) + 1
plt.xlabel('epoch') # 设置x坐标名称
plt.ylabel('RMSE') # 设置y坐标名称
plt.title('训练情况') # 设置标题
plt.plot(x,RMSE,color='r',linestyle='dashed')
plt.plot(x,RMSE2,color='k',linestyle='dashed')
# plt.plot(x,RMSE,color='r') # 设置绘图的基本参数
plt.axis([0,ep+ 1,0,ymax]) # 设置xy的取值范围
plt.show() # 展示图片
实验八 线性回归二分类
# 2-8
# 线性回归对百分制成绩进行二分类
import numpy as np
import matplotlib.pyplot as plt
import random as rd
# parameters
dataset = 2 # index of training dataset
epoch = 2000
sdy = 0.0001
# datasets for training
if dataset == 1: # balanced datasetx_train = np.array([50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70]).reshape((1, -1))y_train = np.array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]).reshape((1, -1))
elif dataset == 2: # unbalanced dataset 1x_train = np.array([0, 5, 10, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70]).reshape((1, -1))y_train = np.array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]).reshape((1, -1))
elif dataset == 3: # unbalanced dataset 2x_train = np.array([0, 5, 10, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73]).reshape((1, -1))y_train = np.array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]).reshape((1, -1))
m_train = x_train.size # number of training examples
w = np.array([0.]).reshape((1, -1))# 权重
b = np.array([0.])# 偏差
# 批梯度下降
for _ in range(epoch):e = np.dot(w,x_train) + b - y_train
# print(e)b -= 2*sdy*np.dot(e,np.ones(m_train))/m_trainw -= 2*sdy*np.dot(x_train,e.transpose())/m_train
# 画图部分
yc = []
yy = []
lines = w[0][0]*60 + b[0]
for i in x_train[0]:datas = w[0][0]*i + b[0]yy.append(datas)yc.append( 1 if datas >= lines else 0)
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
plt.xlabel('分数')
plt.ylabel('结果')
plt.plot(x_train[0],yy)
plt.scatter(x_train[0],yc)
plt.show()实验九 均方差(MSE)-逻辑回归模型
# 2-9
# 均方误差代价函数->逻辑回归模型
import matplotlib.pyplot as plt
import pandas
import numpy as np
import random as rd
# load dataset
df = pandas.read_csv('alcohol_dataset.csv')
data = np.array(df)
y4 = np.array([i[5:] for i in data]) # 标注
y03 = np.array([i[:5] for i in data]) # 4维输入特征
# 标准化
mean = np.mean(y03,0) # 平均值
stds = np.std(y03,0,ddof=1) # 标准差
y03 = (y03-mean)/stds# 标准化完成
# 学习率
xuexi = 0.1
# 训练次数
epoch = 30000
# 区分训练集和测试集
m = len(data) # 样本总长度
__ = [i for i in range(m)]
tram = int(m*0.7) # 训练集长度
tesm = m - tram # 测试集长度
trainx = [] # 训练集输入特征
trainy = [] # 训练集标注
testx = [] # 测试集输入特征
testy = [] # 测试集标注
# 开始随机筛选训练集
for i in range(tram):_ = rd.choice(__)trainx.append(y03[_])trainy.append(y4[_])__.remove(_)
# 剩下的样本就是 测试集合
for i in __:testx.append(y03[i])testy.append(y4[i])
trainx,trainy,testx,testy= np.array(trainx),np.array(trainy),np.array(testx),np.array(testy) # list => np.array
# 设置权重w,和偏差b
w = np.array([0.,0.,0.,0.,0.]).reshape(1,-1)
b = np.array([0.]).reshape(1,-1)
REMS = []
for _ in range(epoch):y = -(np.dot(w,trainx.transpose()) + b) # -wTx + b,1*ny = 1/(1 + np.exp(y)) # 计算1/(1+e(-(wTx+b)))1*n e = y - trainy.transpose() # 计算 e 1*nw -= 2*xuexi*np.dot((y*(1-y)*e),trainx)/tram # 1*4 # 更新wb -= 2*xuexi*np.dot((y*(1-y)),e.transpose()) / tram # 更新b# 测试集REMS 计算y = -(np.dot(w,testx.transpose()) + b) # -wTx + b,1*n y = 1/(1 + np.exp(y)) # 1*n e = y - testy.transpose() # 1*na = np.dot(e,e.transpose())[0][0]/tesmREMS.append(a**0.5)# 绘图部分
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
x = [i for i in range(epoch)]
print(min(REMS))
plt.plot(x,REMS,color='b',linestyle='dashed')
plt.xlabel('epoch')
plt.ylabel('REMS')
plt.title('训练情况')
plt.show()实验九 均方差(MSE)-逻辑回归模型3D版本
# 3D图像展示2-9
import matplotlib.pyplot as plt
import pandas
import numpy as np
import random as rd
# load dataset
df = pandas.read_csv('alcohol_dataset.csv')
data = np.array(df)
y4 = np.array([i[5:] for i in data]) # 标注
y03 = np.array([i[:1] for i in data]) # 1维输入特征
# 标准化
mean = np.mean(y03,0) # 平均值
stds = np.std(y03,0,ddof=1) # 标准差
y03 = (y03-mean)/stds# 标准化完成
# 学习率
xuexi = 0.1
# 训练次数
epoch = 1000
# 区分训练集和测试集
m = len(data) # 样本总长度
__ = [i for i in range(m)]
tram = int(m*0.7) # 训练集长度
tesm = m - tram # 测试集长度
trainx = [] # 训练集输入特征
trainy = [] # 训练集标注
testx = [] # 测试集输入特征
testy = [] # 测试集标注
# 开始随机筛选训练集
for i in range(tram):_ = rd.choice(__)trainx.append(y03[_])trainy.append(y4[_])__.remove(_)
# 剩下的样本就是 测试集合
for i in __:testx.append(y03[i])testy.append(y4[i])
trainx,trainy,testx,testy= np.array(trainx),np.array(trainy),np.array(testx),np.array(testy) # list => np.array
# 设置权重w,和偏差b
w = np.array([10.]).reshape(1,-1)
b = np.array([0.]).reshape(1,-1)
REMS = []
Wchange=[] # w的变化过程
Bchange=[] # B的变化过程
for _ in range(epoch):y = -(np.dot(w,trainx.transpose()) + b) # -wTx + b,1*ny = 1/(1 + np.exp(y)) # 计算1/(1+e(-(wTx+b)))1*n e = y - trainy.transpose() # 计算 e 1*nw -= 2*xuexi*np.dot((y*(1-y)*e),trainx)/tram # 1*4 # 更新wb -= 2*xuexi*np.dot((y*(1-y)),e.transpose()) / tram # 更新b# 测试集REMS 计算y = -(np.dot(w,testx.transpose()) + b) # -wTx + b,1*n y = 1/(1 + np.exp(y)) # 1*n e = y - testy.transpose() # 1*na = np.dot(e,e.transpose())[0][0]/tesmREMS.append(a**0.5)Wchange.append(w[0][0])Bchange.append(b[0][0])# 绘图部分
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
Wchange, Bchange=np.meshgrid(Wchange,Bchange)
_ = REMS[:]
REMS = np.array([_ for i in range(epoch)])
# 绘制3D曲面图
ax.plot_surface(Bchange, Wchange, REMS, cmap='viridis')# 设置图形属性
ax.set_xlabel('X Label')
ax.set_ylabel('Y Label')
ax.set_zlabel('Z Label')
ax.set_title('3D Surface Plot')# 显示图形
plt.show()实验十 交叉熵-逻辑回归模型(R,P,F1)
# 实验2-10
# 交叉熵代价函数
import matplotlib.pyplot as plt
import pandas
import numpy as np
import random as rd
# 基本参数确定
epoch = 10000
xuexi = 0.1
# 加载数据
df = pandas.read_csv('alcohol_dataset.csv')
data = np.array(df)
rng = np.random.default_rng(1)
rng.shuffle(data)
# 训练集和测试集长度确定
split_rate = 0.7
train_m = int(len(data)*split_rate)
test_m = len(data) - train_m
d = len(data[0])-1 # 输入特征维度(从0开始计数)
# 标准化
mean = np.mean(data[:train_m,0:d],0) # 平均值
stds = np.std(data[:train_m,0:d],0,ddof=1)# 标准差
data[:,0:d] = (data[:,0:d]-mean)/stds
# 制作训练集和测试集
print(type(data))
train_X,train_Y, test_X,test_Y= data[:train_m,0:d],data[:train_m,d:],data[train_m:,0:d], data[train_m:,d:]
print(data[:train_m,0:d].shape)
# 初始化权重w和偏差b
w ,b= np.random.rand(1,d),np.random.rand(1,1)
Data = []
def Confusion_matrix(a,b): # 计算召回率,精度,F!分数的函数b = b > 0.5allp = np.sum(b)c = a*bTP = np.sum(c)FP = np.sum(a*(1-c))
# FN = np.sum(b*(1-c))
# TN = train_m - FP-allpR = TP/allpP = TP/(FP+TP)return R,P,2/(1/R + 1/P)
for _A_ in range(epoch):# 利用代价函数更新 w和 be = -(np.dot(w,train_X.transpose())+ b)e = 1/(1 + np.exp(e)) e -= train_Y.transpose() # 1*train_mw -= xuexi*np.dot(e,train_X)/train_mb -= xuexi*np.dot(e,np.ones(train_m).transpose())/train_m# 计算交叉熵和召回率,精度以及F1分数# 训练集e = -(np.dot(w,train_X.transpose())+ b)N_Y = 1/(1 + np.exp(e))J = np.dot(np.log(N_Y),train_Y) +np.dot(np.log(1-N_Y),(1-train_Y)) R,P,F1 = Confusion_matrix(N_Y>=0.5,train_Y[:].transpose())_ = {"R":R,"P":P,"F1":F1,'J1':-J[0][0]/train_m}# 测试集e = -(np.dot(w,test_X.transpose())+ b)N_Y = 1/(1 + np.exp(e))J = np.dot(np.log(N_Y),test_Y) +np.dot(np.log(1-N_Y),(1-test_Y))_['J2'] = -J[0][0]/test_m_['R1'],_['P1'],_['F11'] = Confusion_matrix(N_Y>=0.5,test_Y[:].transpose())Data.append(_)
# 绘图部分
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
fig, axes = plt.subplots(2, 2)
x = [i for i in range(epoch)]
axes[0][0].plot(x,[i['J1'] for i in Data],color='r',linestyle='dashed',label='train')
axes[0][0].plot(x,[i['J2'] for i in Data],color='b',linestyle='dashed',label='test')
axes[0][0].legend()
axes[0][0].set_title('交叉熵')
axes[0][1].plot(x,[i['P'] for i in Data],color='r',linestyle='dashed',label='train')
axes[0][1].plot(x,[i['P1'] for i in Data],color='b',linestyle='dashed',label='test')
axes[0][1].legend()
axes[0][1].set_title('精度')
axes[1][0].plot(x,[i['F1'] for i in Data],color='r',linestyle='dashed',label='train')
axes[1][0].plot(x,[i['F11'] for i in Data],color='b',linestyle='dashed',label='test')
axes[1][0].set_title('F1分数')
axes[1][0].legend()
axes[1][1].plot(x,[i['R'] for i in Data],color='r',linestyle='dashed',label='train')
axes[1][1].plot(x,[i['R1'] for i in Data],color='b',linestyle='dashed',label='test')
axes[1][1].set_title('召回率')
axes[1][1].legend()
plt.tight_layout()
plt.show()实验十一 scikit-learn SVM
# 2-11
# scikit-learn支持向量机
import matplotlib.pyplot as plt
import pandas
import numpy as np
import random as rd
from sklearn import svm
# 基本参数确定
epoch = 10000
xuexi = 0.1
# 加载数据
df = pandas.read_csv('alcohol_dataset.csv')
data = np.array(df)
rng = np.random.default_rng(1)
rng.shuffle(data)
# 训练集和测试集长度确定
split_rate = 0.7
train_m = int(len(data)*split_rate)
test_m = len(data) - train_m
d = len(data[0])-1 # 输入特征维度(从0开始计数)
# 标准化
mean = np.mean(data[:train_m,0:d],0) # 平均值
stds = np.std(data[:train_m,0:d],0,ddof=1)# 标准差
data[:,0:d] = (data[:,0:d]-mean)/stds
data[:,d:] = data[:,d:]+(data[:,d:]-1) # 将标注0改为1
# 制作训练集和测试集
train_X,train_Y, test_X,test_Y= data[:train_m,0:d],data[:train_m,d:],data[train_m:,0:d], data[train_m:,d:]
Call = [0.1,1,10,100,1000]
kernels = ['linear','poly','rbf']
data=[["线性核"],["多项式核"],["高斯核"]]
for i in Call:for j in kernels:clf = svm.SVC(C=i, kernel=j) #linear 线性核函数 poly 多项式核函数,rbf高斯径向基核函数(默认)clf.fit(train_X, train_Y.ravel())te = clf.predict(test_X)-test_Y.ravel()ta = clf.predict(train_X)-train_Y.ravel()te*=teta*=tate = int(np.sum(te))//4ta = int(np.sum(ta))//4data[kernels.index(j)].append("%d(%d+%d)"%(te+ta,ta,te))
# print("C=%f 核函数:%s %d(%d+%d)"%(i,j,te+ta,ta,te))
# 表格绘制
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
# print(data)
fig, ax = plt.subplots()
ax.axis('off') # 隐藏坐标轴# 创建表格,设置文本居中
table = ax.table(cellText=data, colLabels=['核函数', 'C=0.1', 'C=1', 'C=10', 'C=100', 'C=1000'], cellLoc='center', loc='center')# 设置表格样式
table.auto_set_font_size(False)
table.set_fontsize(14)
table.scale(1.2, 1.2) # 放大表格plt.show()实验十二 SVM(错误率随C值变化)
# 2-12
# 错误随c的变化
import matplotlib.pyplot as plt
import pandas
import numpy as np
import random as rd
from sklearn import svm
# 基本参数确定
epoch = 10000
xuexi = 0.1
# 加载数据
df = pandas.read_csv('alcohol_dataset.csv')
data = np.array(df)
rng = np.random.default_rng(1)
rng.shuffle(data)
# 训练集和测试集长度确定
split_rate = 0.7
train_m = int(len(data)*split_rate)
test_m = len(data) - train_m
d = len(data[0])-1 # 输入特征维度(从0开始计数)
# 标准化
mean = np.mean(data[:train_m,0:d],0) # 平均值
stds = np.std(data[:train_m,0:d],0,ddof=1)# 标准差
data[:,0:d] = (data[:,0:d]-mean)/stds
data[:,d:] = data[:,d:]+(data[:,d:]-1) # 将标注0改为1
# 制作训练集和测试集
train_X,train_Y, test_X,test_Y= data[:train_m,0:d],data[:train_m,d:],data[train_m:,0:d], data[train_m:,d:]
Call =list(np.random.uniform(0.1, 16, 150))
Call.sort()
kernels = ['linear','poly','rbf']
tadata=[[],[],[]]
tedata=[[],[],[]]
for i in Call:for j in kernels:clf = svm.SVC(C=i, kernel=j) #linear 线性核函数 poly 多项式核函数,rbf高斯径向基核函数(默认)clf.fit(train_X, train_Y.ravel())te = clf.predict(test_X)-test_Y.ravel()ta = clf.predict(train_X)-train_Y.ravel()te*=teta*=tate = int(np.sum(te))//4ta = int(np.sum(ta))//4tadata[kernels.index(j)].append(ta)tedata[kernels.index(j)].append(te)
# 绘图部分
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
fig, axes = plt.subplots(2, 2)
x =Call
axes[0][0].plot(x,tadata[0],color='r',label='train',marker='x')
axes[0][0].plot(x,tedata[0],color='b',label='test',marker='o')
axes[0][0].legend()
axes[0][0].set_title('线性核')
axes[0][1].plot(x,tadata[1],color='r',label='train',marker='x')
axes[0][1].plot(x,tedata[1],color='b',label='test',marker='o')
axes[0][1].legend()
axes[0][1].set_title('多项式核')
axes[1][0].plot(x,tadata[2],color='r',label='train',marker='x')
axes[1][0].plot(x,tedata[2],color='b',label='test',marker='o')
axes[1][0].legend()
axes[1][0].set_title('高斯核心')
axes[1, 1].axis('off')# 隐蔽第四个
plt.tight_layout()
plt.show()实验十三 K交叉验证-SVM
# 2-13
# k交叉验证 错误随c的变化
import matplotlib.pyplot as plt
import pandas
import numpy as np
import random as rd
from sklearn import svm
# 基本参数确定
epoch = 10000
xuexi = 0.1
k = 4 # 重交叉验证k的值
# 加载数据
df = pandas.read_csv('alcohol_dataset.csv')
data = np.array(df)
rng = np.random.default_rng(100)
rng.shuffle(data)
# 训练集和测试集长度确定
split_rate = 0.7
alllines = len(data)
train_m = int(alllines*((k-1)/k))
test_m = alllines - train_m
d = len(data[0])-1 # 输入特征维度(从0开始计数)
# 标准化
mean = np.mean(data[:train_m,0:d],0) # 平均值
stds = np.std(data[:train_m,0:d],0,ddof=1)# 标准差
data[:,0:d] = (data[:,0:d]-mean)/stds
data[:,d:] = data[:,d:]+(data[:,d:]-1) # 将标注0改为1
# 制作训练集和测试集
# train_X,train_Y, test_X,test_Y= data[:train_m,0:d],data[:train_m,d:],data[train_m:,0:d], data[train_m:,d:]
Call =list(np.random.uniform(0.1, 10, 25))
Call.sort()
kernels = ['linear','poly','rbf']
tadata=[[],[],[]]
tedata=[[],[],[]]
for i in Call:for j in kernels:tadata1=[]tedata1=[]id = kernels.index(j)for t in range(k):start = t*test_mends = (t+1)*test_m if ((t+1)*test_m ) <= alllines else alllinesif t == 0:train_X,train_Y= data[ends:alllines,0:d],data[ends:alllines,d:]elif t == 3:train_X,train_Y= data[0:start,0:d],data[0:start,d:]else:train_X,train_Y= np.concatenate((data[0:start,0:d],data[ends:alllines,0:d]),0),np.concatenate((data[0:start,d:],data[ends:alllines,d:]),0)test_X,test_Y=data[start:ends,0:d], data[start:ends:,d:]clf = svm.SVC(C=i, kernel=j) #linear 线性核函数 poly 多项式核函数,rbf高斯径向基核函数(默认)clf.fit(train_X, train_Y.ravel())te = clf.predict(test_X)-test_Y.ravel()ta = clf.predict(train_X)-train_Y.ravel()te*=teta*=tate = int(np.sum(te))//4ta = int(np.sum(ta))//4tadata1.append(ta)tedata1.append(te)tadata[id].append(sum(tadata1)/k)tedata[id].append(sum(tedata1)/k)
# 绘图部分
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
fig, axes = plt.subplots(2, 2)
x =Call
axes[0][0].plot(x,tadata[0],color='r',label='train',marker='x')
axes[0][0].plot(x,tedata[0],color='b',label='test',marker='o')
axes[0][0].legend()
axes[0][0].set_title('线性核')
axes[0][1].plot(x,tadata[1],color='r',label='train',marker='x')
axes[0][1].plot(x,tedata[1],color='b',label='test',marker='o')
axes[0][1].legend()
axes[0][1].set_title('多项式核')
axes[1][0].plot(x,tadata[2],color='r',label='train',marker='x')
axes[1][0].plot(x,tedata[2],color='b',label='test',marker='o')
axes[1][0].legend()
axes[1][0].set_title('高斯核心')
axes[1, 1].axis('off')# 隐蔽第四个
plt.tight_layout()
plt.show()实验十四 K近邻(K变化)-K交叉验证
# 2-14
# 经典求解 k近邻
import matplotlib.pyplot as plt
import pandas
import numpy as np
from scipy import stats
# load dataset
df = pandas.read_csv('wheelchair_dataset.csv')
data = np.array(df)
data=data.astype(np.float64)
# 随机排序
rng = np.random.default_rng(400)
rng.shuffle(data)
# 输入特征维度
d = data.shape[1] - 1
# 数据最大最小归一化处理
maxs = np.amax(data[:,0:d],0)
mins = np.amin(data[:,0:d],0)
data[:,0:d] = (data[:,0:d] - mins) / (maxs - mins)
# 样本长度
lens = data.shape[0]
# 设置k交叉验证中 k的值
k = 4
# 测试集长度
test_m = lens // k
# k近邻分类 中的k值
kk = [i for i in range(1,21)]
Error = [[],[]]
for i in kk:ta = 0te = 0for j in range(k):# 区分训练集和测试集start = j*test_mends = (j+1)*test_m if (j != k-1) else lensif j == 0:train_x,train_y = data[ends:,0:d],data[ends:,d:]elif j == k -1:train_x,train_y = data[0:start,0:d],data[0:start,d:]else:train_x,train_y=np.concatenate((data[0:start,0:d],data[ends:,0:d]),0),np.concatenate((data[0:start,d:],data[ends:,d:]),0)test_x,test_y = data[start:ends,0:d],data[start:ends,d:]# 计算距离ans = 0 # 测试集错误率 for t in range(len(test_x)):_ = np.sum((train_x-test_x[t])*(train_x-test_x[t]),1)# 得到全部的距离__ = np.argsort(_) # 排序for h in range(i, len(_)):if _[__[h]] != _[__[h-1]]:break_ = [train_y[hh] for hh in __[:h]]if test_y[t] != stats.mode(_,keepdims=False)[0][0]:ans += 1te += ans
# print(ans)# 计算距离ans = 0 # 测试集错误率 for t in range(len(train_x)):_ = np.sum((train_x-train_x[t])*(train_x-train_x[t]),1)# 得到全部的距离__ = np.argsort(_)for h in range(i, len(_)):if _[__[h]] != _[__[h-1]]:break_ = [train_y[hh] for hh in __[:h]]if train_y[t] != stats.mode(_,keepdims=False)[0][0]:ans += 1ta += ansError[0].append(ta/k)Error[1].append(te/k)
# 绘图部分
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
plt.plot(kk,Error[0],color='r',marker='o',label='train')
plt.plot(kk,Error[1],color='b',marker='x',label='test')
plt.legend()
plt.show()实验十五 宏F1值,马修斯相关系数
# 2-15
# 马修斯相关系数计算 k近邻
# 1姿势正确,2坐姿偏右,3坐姿偏左,4坐姿前倾
import matplotlib.pyplot as plt
import pandas
import numpy as np
from scipy import stats
# load dataset
df = pandas.read_csv('wheelchair_dataset.csv')
data = np.array(df)
# 随机排序
rng = np.random.default_rng(100)
rng.shuffle(data)
data=data.astype(np.float64)
# 输入特征维度
d = data.shape[1] - 1
# 数据最大最小归一化处理
maxs = np.amax(data[:,0:d],0)
mins = np.amin(data[:,0:d],0)
data[:,0:d] = (data[:,0:d] - mins) / (maxs - mins)
# 样本长度
lens = data.shape[0]
# 设置k交叉验证中 k的值
k = 4
# 测试集长度
test_m = lens // k
# k近邻分类 中的k值
kk = [i for i in range(1,21)]
Error = [[],[],[],[]]
# 求宏平均F1分数
for i in kk:ta,te,tta,tte = 0.,0.,0.,0.for j in range(k):tag_= []teg_= []# 区分训练集和测试集start = j*test_mends = (j+1)*test_m if (j != k-1) else lensif j == 0:train_x,train_y = data[ends:,0:d],data[ends:,d:]elif j == k -1:train_x,train_y = data[0:start,0:d],data[0:start,d:]else:train_x,train_y=np.concatenate((data[0:start,0:d],data[ends:,0:d]),0),np.concatenate((data[0:start,d:],data[ends:,d:]),0)test_x,test_y = data[start:ends,0:d],data[start:ends,d:]# 计算距离for t in range(len(test_x)):_ = np.sum((train_x-test_x[t])*(train_x-test_x[t]),1)# 得到全部的距离__ = np.argsort(_) # 排序for h in range(i, len(_)):if _[__[h]] != _[__[h-1]]:break_ = [train_y[hh] for hh in __[:h]]teg_.append(int(stats.mode(_,keepdims=False)[0][0]))# 计算距离teg_ = np.array(teg_).reshape(1,-1)for t in range(len(train_x)):_ = np.sum((train_x-train_x[t])*(train_x-train_x[t]),1)# 得到全部的距离__ = np.argsort(_)for h in range(i, len(_)):if _[__[h]] != _[__[h-1]]:break_ = [train_y[hh] for hh in __[:h]]tag_.append(int(stats.mode(_,keepdims=False)[0][0]))# 计算F1分数# 计算方法就是 测试集和训练集分别一个宏均F1分数,# 其次采用了k交叉验证,最终的F1分数是这k次计算结果的宏均F1的平均值tag_ = np.array(tag_).reshape(1,-1)def G(a,b):allp = np.sum(b)c = a*bTP = np.sum(c)FP = np.sum(a*(1-c))if FP + TP == 0:return 0R = TP/allpP = TP/(FP+TP)if not P:return 0return 2/(1/R + 1/P)def getF1(li1,li2):a,b,c,d = li1==4,li1==3,li1==2,li1==1a1,b1,c1,d1 = li2==4.,li2==3.,li2==2.,li2==1.return (G(a,a1)+G(b,b1)+G(c,c1)+G(d,d1))/4te += getF1(teg_,test_y.transpose())ta += getF1(tag_,train_y.transpose())# 计算马修斯相关系数def getMCC(li1,li2):a,b,c,d = li1==4,li1==3,li1==2,li1==1a1,b1,c1,d1 = li2==4.,li2==3.,li2==2.,li2==1.A = len(li1[0])S = np.sum(a*a1)+np.sum(b*b1)+np.sum(c*c1)+np.sum(d*d1)h = np.array([np.sum(a) , np.sum(b) , np.sum(c) , np.sum(d)])l = np.array([np.sum(a1) , np.sum(b1),np.sum(c1) , np.sum(d1)])_ = A*S - np.sum(h*l)__ = ((A*A - np.sum(h*h))*(A*A-np.sum(l*l)))**0.5return _/__tte += getMCC(teg_,test_y.transpose())tta += getMCC(tag_,train_y.transpose())Error[0].append(ta/k)Error[1].append(te/k)Error[2].append(tta/k)Error[3].append(tte/k)
# 绘图部分
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
fig, axes = plt.subplots(nrows=1, ncols=2)
axes[0].plot(kk,Error[0],color='r',linestyle='dashed',label='train',marker='x')
axes[0].plot(kk,Error[1],color='b',linestyle='dashed',label='test',marker='o')
axes[0].legend()
axes[0].set_title('宏平均F1')
axes[1].plot(kk,Error[2],color='r',linestyle='dashed',label='train',marker='x')
axes[1].plot(kk,Error[3],color='b',linestyle='dashed',label='test',marker='o')
axes[1].legend()
axes[1].set_title('MCC')
plt.tight_layout()
plt.show()
实验十六 高斯朴素贝叶斯分类器
# 高斯朴素贝叶斯分类器 2-16
# 1姿势正确,2坐姿偏右,3坐姿偏左,4坐姿前倾
import matplotlib.pyplot as plt
import pandas
import numpy as np
from scipy import stats
# load dataset
df = pandas.read_csv('wheelchair_dataset.csv')
data = np.array(df)
# 随机排序
rng = np.random.default_rng(1)
rng.shuffle(data)
data=data.astype(np.float64)
# 输入特征维度
d = data.shape[1] - 1
# 样本长度
lens = data.shape[0]
# 设置k交叉验证中 k的值
k = 4
# 测试集长度
test_m = lens // k
# k近邻分类 中的k值
kk = [i for i in range(1,21)]
Error = [[],[],[],[]]
# 求宏平均F1分数
for i in kk:ta,te,tta,tte = 0.,0.,0.,0.for j in range(k):tag_= []teg_= []# 区分训练集和测试集start = j*test_mends = (j+1)*test_m if (j != k-1) else lensif j == 0:train_x,train_y = data[ends:,0:d],data[ends:,d:]elif j == k -1:train_x,train_y = data[0:start,0:d],data[0:start,d:]else:train_x,train_y=np.concatenate((data[0:start,0:d],data[ends:,0:d]),0),np.concatenate((data[0:start,d:],data[ends:,d:]),0)test_x,test_y = data[start:ends,0:d],data[start:ends,d:]# 高斯朴素贝叶斯# 计算ujk 和 pckdef getUjkAndPck(lia,lib):ujk = np.array([[0. for _ in range(4)] for __ in range(d)]) # d *4 的矩阵,输入特征维度*类别总数times = [0 for _ in range (4)]for tt in range(len(lib)):kk = int(lib[tt])-1 # 得到的是 类别ujk[:,kk] += lia[tt] # 注意横纵坐标的含义times[kk] += 1for _ in range(d):ujk[_] /= times return ujk,np.array(times)/len(lia)# 方差的无偏估计量def getOjk2(lia,lib,ujk):Ojk2 = np.array([[0. for _ in range(4)] for __ in range(d)])times = [0 for i in range(4)]for _ in range(len(lib)):kk = int(lib[_])-1Ojk2[:,kk] += (lia[_] - ujk[:,kk])**2 # 注意横纵坐标的含义times[kk] += 1times = np.array(times)-1for _ in range(d):Ojk2[_] /= timesreturn Ojk2**0.5ujk,pck = getUjkAndPck(train_x,train_y.transpose()[0])Ojk2 = getOjk2(train_x,train_y.transpose()[0],ujk)# 测试集for _ in test_x:__ = (ujk.transpose() - _)/Ojk2.transpose()__ = __**2__ = np.log(pck)-0.5*np.sum(__,1) -np.sum(np.log(Ojk2).transpose(),1)teg_.append(np.argmax(__)+1)teg_ = np.array(teg_).reshape(1,-1)# 训练集for _ in train_x:__ = (ujk.transpose() - _)/Ojk2.transpose()__ = __**2__ = np.log(pck)-0.5*np.sum(__,1) -np.sum(np.log(Ojk2).transpose(),1)tag_.append(np.argmax(__)+1)tag_ = np.array(tag_).reshape(1,-1)# 计算F1分数# 计算方法就是 测试集和训练集分别一个宏均F1分数,# 其次采用了k交叉验证,最终的F1分数是这k次计算结果的宏均F1的平均值def G(a,b):allp = np.sum(b)c = a*bTP = np.sum(c)FP = np.sum(a*(1-c))if FP + TP == 0:return 0R = TP/allpP = TP/(FP+TP)if not P:return 0return 2/(1/R + 1/P)def getF1(li1,li2):a,b,c,d = li1==4,li1==3,li1==2,li1==1a1,b1,c1,d1 = li2==4.,li2==3.,li2==2.,li2==1.return (G(a,a1)+G(b,b1)+G(c,c1)+G(d,d1))/4te += getF1(teg_,test_y.transpose())ta += getF1(tag_,train_y.transpose())# 计算马修斯相关系数def getMCC(li1,li2):a,b,c,d = li1==4,li1==3,li1==2,li1==1a1,b1,c1,d1 = li2==4.,li2==3.,li2==2.,li2==1.A = len(li1[0])S = np.sum(a*a1)+np.sum(b*b1)+np.sum(c*c1)+np.sum(d*d1)h = np.array([np.sum(a) , np.sum(b) , np.sum(c) , np.sum(d)])l = np.array([np.sum(a1) , np.sum(b1),np.sum(c1) , np.sum(d1)])_ = A*S - np.sum(h*l)__ = ((A*A - np.sum(h*h))*(A*A-np.sum(l*l)))**0.5return _/__tte += getMCC(teg_,test_y.transpose())tta += getMCC(tag_,train_y.transpose())Error[0].append(ta/k)Error[1].append(te/k)Error[2].append(tta/k)Error[3].append(tte/k)
# 绘图部分
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
fig, axes = plt.subplots(nrows=1, ncols=2)
axes[0].plot(kk,Error[0],color='r',linestyle='dashed',label='train',marker='x')
axes[0].plot(kk,Error[1],color='b',linestyle='dashed',label='test',marker='o')
axes[0].legend()
axes[0].set_title('宏平均F1')
axes[1].plot(kk,Error[2],color='r',linestyle='dashed',label='train',marker='x')
axes[1].plot(kk,Error[3],color='b',linestyle='dashed',label='test',marker='o')
axes[1].legend()
axes[1].set_title('MCC')
plt.tight_layout()
plt.show()
实验十七 多分类逻辑回归
# 多分类逻辑回归 2-17
# 1姿势正确,2坐姿偏右,3坐姿偏左,4坐姿前倾
import matplotlib.pyplot as plt
import pandas
import numpy as np
from scipy import stats
import random as rd
# load dataset
df = pandas.read_csv('wheelchair_dataset.csv')
data = np.array(df)
# 随机排序
rng = np.random.default_rng(1)
rng.shuffle(data)
data=data.astype(np.float64)
# 输入特征维度
d = data.shape[1] - 1
# 样本长度
lens = data.shape[0]
# 设置训练次数
epochs = 5000
# 设置学习率
xuexi = 0.1
# 标准化处理
mean = np.mean(data[:,:d],0)
stds = np.std(data[:,:d],0,ddof=1)
data[:,:d] = (data[:,:d]-mean)/stds
# 多分类逻辑回归
# 初始化 w,b
w = np.array([[rd.uniform(0,1) for __ in range(d)] for _ in range(4)]) # c * d
b = np.array([[rd.uniform(0,1) ] for _ in range(4)]) # c*1
# y-> one-hot
datay = np.array([[i==1.,i==2.,i==3.,i==4.] for i in data[:,d]])
# 划分数据集和测试集
train_m = int(lens*0.8)
test_m = lens - train_m
train_x,train_y,test_x,test_y = data[:train_m,:d],datay[:train_m],data[train_m:,:d],datay[train_m:]# x:m*d,y:m*c
Errors = [[],[],[],[]]
for _ in range(epochs):# 更新w,b# 第一步计算 ZZ = np.dot(w,train_x.transpose()) + np.dot(b,np.ones(train_m).reshape(1,-1))# 计算 Y^_ = np.random.rand(4,4)>0 # c*c矩阵Y_ = np.exp(Z)/np.dot(_,np.exp(Z)) # c*m# 计算 EE = Y_ - train_y.transpose() # c*m# 计算多类别逻辑回归交叉熵TaJwb = np.trace(np.dot(train_y,np.log(Y_)))/-train_mErrors[2].append(TaJwb)# 统计训练集出错_ = np.argmax(Y_,0) + 1_ = _.astype(np.float64)_ -= data[:train_m,d]taer = np.sum(_ > 0)taer += np.sum(_ < 0)Errors[0].append(taer)# 统计测试集出错# 第一步计算 ZZ = np.dot(w,test_x.transpose()) + np.dot(b,np.ones(test_m).reshape(1,-1))# 计算 Y^_ = np.random.rand(4,4)>0 # c*c矩阵Y_ = np.exp(Z)/np.dot(_,np.exp(Z)) # c*m_ = np.argmax(Y_,0) + 1_ = _.astype(np.float64)_ -= data[train_m:,d]teer = np.sum(_ > 0)teer += np.sum(_ < 0)Errors[1].append(teer)# 更新w,bb -= np.dot(E,np.ones(train_m).reshape(-1,1))/train_mw -= np.dot(E,train_x)/train_m
# 绘图部分
print(Errors[0][-1],Errors[1][-1],Errors[2][-1])
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
fig, axes = plt.subplots(nrows=1, ncols=2)
kk = [i for i in range(epochs)]
axes[0].plot(kk,Errors[0],color='r',linestyle='dashed',label='train',marker='x')
axes[0].plot(kk,Errors[1],color='b',linestyle='dashed',label='test',marker='x')
axes[0].legend()
axes[0].set_title('trainErrors')
axes[1].plot(kk,Errors[2],color='r',linestyle='dashed',label='train',marker='x')
axes[1].legend()
axes[1].set_title('交叉熵')
plt.tight_layout()
plt.show()二分类逻辑回归的不足
# 二分类逻辑回归对其进行预测
import numpy as np
import random as rd
x_train = np.array([0, 5, 10, 25, 30, 35, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73]).reshape((1, -1))
y_train = np.array([0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]).reshape((1, -1))
m_train = x_train.size # number of training examples
# 第一步随机排序 (这里感觉不用)
epoch = 30000 # 训练次数
xuexi = 0.0001 # 学习率
# 设置权重和偏差
w = 0.
b = 0.
for _ in range(epoch):# 第一步计算eY_ = 1/(1+np.exp(-(w*x_train + b)))e = Y_ - y_train# 更新 w,bb -= xuexi*np.dot(e,np.ones(m_train).transpose())/m_trainw -= xuexi*np.dot(x_train,e.transpose())/m_train
# 绘图部分
Y = 1/(1+np.exp(-(w*x_train + b)))
print(Y)
# lines = 60*w + b
Y_= Y >= 0.5
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号kk = [i for i in range(epochs)]
plt.plot(x_train[0],Y[0],color='k',linestyle='dashed',label='train')
plt.plot(x_train[0],Y_[0],color='r',linestyle='dashed',label='predict')
plt.scatter(x_train,y_train[0],color='b',label='原本',marker='x')
plt.legend()
plt.title('变化')
plt.tight_layout()
plt.show()二分类逻辑回归强化
# 二分类逻辑回归对其进行预测
# 强化
import matplotlib.pyplot as plt
import pandas
import numpy as np
from scipy import stats
import random as rd
x_train = np.array([0, 5, 10, 25, 30, 35, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73]).reshape((1, -1))
y_train = np.array([0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]).reshape((1, -1))
m_train = x_train.size # number of training examples
# 第一步随机排序 (这里感觉不用)
epoch = 30000 # 训练次数
xuexi = 0.001 # 学习率
# 设置权重和偏差
# 标准化
x_train=x_train.astype(np.float64)
mean = np.mean(x_train,1)
stds = np.std(x_train,1,ddof=1)
x_train = (x_train - mean)/stds
w0,w1,w2,w3 = 0.,0.,0.,0.
b0,b1,b2,b3 = 0.,0.,0.,0.
for _ in range(epoch):# 第一步计算e0Y_ = 1/(1+np.exp(-(w0*x_train + b0)))e = Y_ - y_train# 更新 w0,b0b0 -= xuexi*np.dot(e,np.ones(m_train).transpose())/m_trainw0 -= xuexi*np.dot(x_train,e.transpose())/m_train# 第一步计算e1Y_ = 1/(1+np.exp(-(w1*x_train + b1)+17.5))e = Y_ - y_train# 更新 w,bb1 -= xuexi*np.dot(e,np.ones(m_train).transpose())/m_trainw1 -= xuexi*np.dot(x_train,e.transpose())/m_train# 第一步计算e2Y_ = 1/(1+np.exp(-(w2*x_train + b2) - 42.5))e = Y_ - y_train# 更新 w,bb2 -= xuexi*np.dot(e,np.ones(m_train).transpose())/m_trainw2 -= xuexi*np.dot(x_train,e.transpose())/m_train# 第一步计算e3Y_ = 1/(1+np.exp(-(w3*x_train + b3) + 60))e = Y_ - y_train# 更新 w,bb3 -= xuexi*np.dot(e,np.ones(m_train).transpose())/m_trainw3 -= xuexi*np.dot(x_train,e.transpose())/m_train
# 绘图部分
Y0 = 1/(1+np.exp(-(w0*x_train + b0)))
Y1 = 1/(1+np.exp(-(w1*x_train + b1)+17.5))
Y2 = 1/(1+np.exp(-(w2*x_train + b2)-42.5))
Y3 = 1/(1+np.exp(-(w3*x_train + b3)+60))
Y_ = [-1 for i in range(m_train)]
Yx = Y1+Y2+Y3 -1
# lines = 60*w + b
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
plt.plot(x_train[0],Y0[0],color='k',linestyle='dashed',label='原本的',linewidth=3)
plt.plot(x_train[0],Y1[0],color='#ec2d7a',linestyle='dashdot',label='17.5',linewidth=3)
plt.plot(x_train[0],Y2[0],color='g',linestyle='solid',label='-42.5',linewidth=3)
plt.plot(x_train[0],Y3[0],color='darkviolet',linestyle=(2,(1,2,3,4,2,2)),label='+60',linewidth=3)
plt.plot(x_train[0],Y_,color='r',linestyle='solid',label='-1',linewidth=3)
plt.plot(x_train[0],Yx[0],color='springgreen',linestyle='dotted',label='混合',linewidth=3)
plt.scatter(x_train,y_train[0],color='b',label='原本',marker='x')
plt.legend()
plt.title('变化')
plt.tight_layout()
plt.show()实验十八 二分类神经网络
# 2-18
# 实现二分类神经网络
# 导入酒驾数据
# d = 5
import matplotlib.pyplot as plt
import pandas
import numpy as np
from scipy import stats
import random as rd
# load dataset
df = pandas.read_csv('alcohol_dataset.csv')
data = np.array(df)
# 随机排序
rng = np.random.default_rng(1)
rng.shuffle(data)
# 输入特征维度
d = data.shape[1] -1
# 训练次数
epoch = 300000
# 学习率
XX = 0.00001
# 最大最小归一化
maxs = np.max(data[:,:d],0)
mins = np.min(data[:,:d],0)data[:,:d] = (data[:,:d]-mins)/(maxs-mins)
# mean = np.mean(data[:,:d],0)
# stds = np.std(data[:,:d],0,ddof=1)
# data[:,:d] = (data[:,:d]-mean)/stds
# 训练集测试集划分
train_m = int(data.shape[0]*0.8)
test_m = data.shape[0] - train_m
train_x,train_y,test_x,test_y = data[:train_m,:d],data[:train_m,d:],data[train_m:,:d],data[train_m:,d:]
# train_x m*d, train_y m*1, test_x m*d
# 设置隐含层节点数
n = 2
# 初始化初始权重w1 d*n和偏差 b1 n*1
w1 = np.array([[rd.uniform(0,1) for _ in range(n)] for __ in range(d)])
b1 = np.array([rd.uniform(0,1) for i in range(n)]).reshape(-1,1)
# 初始化初始权重 w2 n*1 和偏差 b2 是常数
w2 = np.array([rd.uniform(0,1) for _ in range(n)]).reshape(-1,1)
b2 = rd.uniform(0,1)
# 存储错误
Errors = [[],[]]
# 激活函数
def ReLU(x):global nreturn np.maximum(0, x).reshape(n,-1)
# 训练
for _ in range(epoch):# 求训练集预测值部分# 第一步计算 Z1 n*mZ1 = np.dot(w1.transpose(),train_x.transpose()) + np.dot(b1,np.ones(train_m).reshape(1,-1))# 激活函数是ReLU 计算A1 n*mA1 = ReLU(Z1)# 计算Z2 1*mZ2 = np.dot(w2.transpose(),A1) + b2# 输出层使用的是sigmoid 激活函数 ,预测值为 predict_ypredict_y = 1/(1+np.exp(-Z2))# 更新权重部分# e 计算 m*1e = predict_y.transpose() - train_ypredict_y ,train_y= predict_y.transpose()>=0.5,train_y >= 0.5Errors[0].append(np.sum(predict_y^train_y))# 更新 b1b1 -= XX*w2*np.dot(A1,e)/train_m# 更新 w1w1 -= XX*np.dot(train_x.transpose(),((np.dot(w2,e.transpose()))*A1).transpose())# 更新b2b2 -= XX*np.dot(np.ones(train_m).reshape(1,-1),e)/train_m# 更新 w2w2 -= XX*np.dot(A1,e)/train_m# 求测试集预测值部分# 第一步计算 Z1 n*mZ1 = np.dot(w1.transpose(),test_x.transpose()) + np.dot(b1,np.ones(test_m).reshape(1,-1))# 激活函数是ReLU 计算A1 n*mA1 = ReLU(Z1)# 计算Z2 1*mZ2 = np.dot(w2.transpose(),A1) + b2# 输出层使用的是sigmoid 激活函数 ,预测值为 predict_ypredict_y = 1/(1+np.exp(-Z2))# 更新权重部分 predict_y ,test_y= predict_y.transpose()>=0.5,test_y >= 0.5Errors[1].append(np.sum(predict_y^test_y))# 绘图部分
print(min(Errors[0]),min(Errors[1]))
X = [i+1 for i in range(epoch)]
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
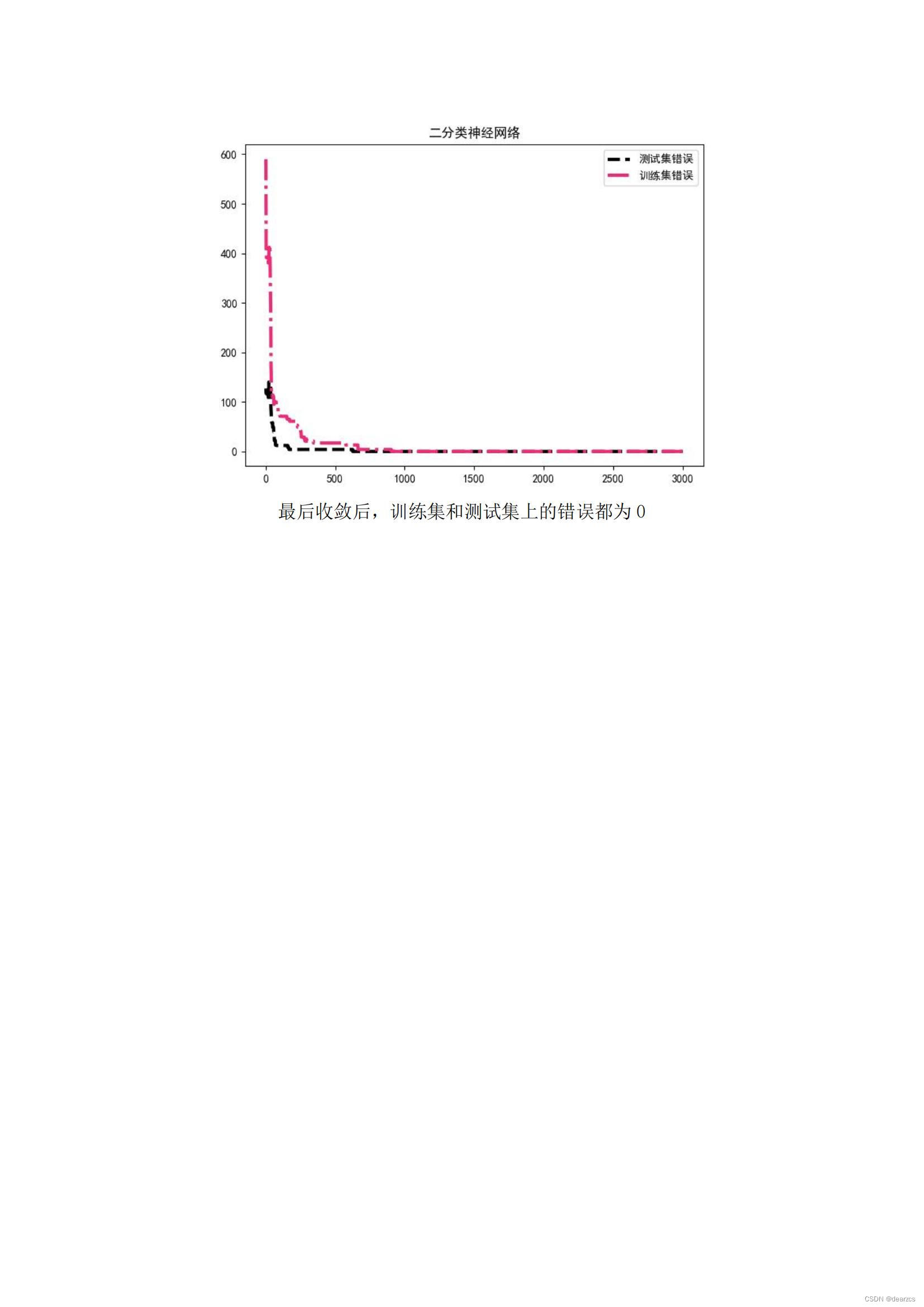
plt.plot(X,Errors[1],color='k',linestyle='dashed',label='测试集错误',linewidth=3)
plt.plot(X,Errors[0],color='#ec2d7a',linestyle='dashdot',label='训练集错误',linewidth=3)
plt.legend()
plt.title('二分类神经网络')
plt.tight_layout()
plt.show()实验十九 多分类神经网络
# 2-19
# 实现多分类神经网络
# 1姿势正确,2坐姿偏右,3坐姿偏左,4坐姿前倾
# d = 4
import matplotlib.pyplot as plt
import pandas
import numpy as np
from scipy import stats
import random as rd
# load dataset
df = pandas.read_csv('wheelchair_dataset.csv')
data = np.array(df)
data=data.astype(np.float64)
# 随机排序
rng = np.random.default_rng(1)
rng.shuffle(data)
# 输入特征维度
d = data.shape[1] -1
# 训练次数
epoch = 3000
# 学习率
XX = 0.1
# 最大最小归一化
# maxs = np.max(data[:,:d],0)
# mins = np.min(data[:,:d],0)
# data[:,:d] = (data[:,:d]-mins)/(maxs-mins)
mean = np.mean(data[:,:d],0)
stds = np.std(data[:,:d],0,ddof=1)
data[:,:d] = (data[:,:d]-mean)/stds
# 训练集测试集划分
train_m = int(data.shape[0]*0.8)
test_m = data.shape[0] - train_m
train_x,train_y,test_x,test_y = data[:train_m,:d],data[:train_m,d:],data[train_m:,:d],data[train_m:,d:]
train_y,test_y = train_y.transpose(),test_y.transpose()
train_y,test_y = np.array([train_y[0]==1.,train_y[0]==2.,train_y[0]==3.,train_y[0]==4.]),np.array([test_y[0]==1.,test_y[0]==2.,test_y[0]==3.,test_y[0]==4.])
# train_x m*d, train_y c*m, test_x m*d
# 设置隐含层节点数
n = 3
# 初始化初始权重w1 d*n和偏差 b1 n*1
w1 = np.array([[rd.uniform(0,1) for _ in range(n)] for __ in range(d)])
b1 = np.array([rd.uniform(0,1) for i in range(n)]).reshape(-1,1)
# 初始化初始权重 w2 n*c 和偏差 b2 c*1
w2 = np.array([[rd.uniform(0,1) for _ in range(4)] for __ in range(n)])
b2 = np.array([rd.uniform(0,1) for i in range(4)]).reshape(-1,1)
# 存储错误
Errors = [[],[]]
# 激活函数
def ReLU(x):global nreturn np.maximum(0, x).reshape(n,-1)
# 训练
for _ in range(epoch):# 求训练集预测值部分# 第一步计算 Z1 n*mZ1 = np.dot(w1.transpose(),train_x.transpose()) + np.dot(b1,np.ones(train_m).reshape(1,-1))# 激活函数是ReLU 计算A1 n*mA1 = ReLU(Z1)# 计算Z2 c*mZ2 = np.dot(w2.transpose(),A1) + np.dot(b2,np.ones(train_m).reshape(1,-1))# 输出层使用的是sigmoid 激活函数 ,预测值为 predict_ypredict_y = np.exp(Z2)/np.dot(np.ones(4*4).reshape(4,4),np.exp(Z2))# 更新权重部分# E 计算 c*mE = predict_y - train_y# 统计错误e = np.argmax(predict_y,0)-np.argmax(train_y,0)Errors[0].append(np.sum(e*e))# 更新 b1
# print('w2',w2.shape,'E',E.shape,'A1',A1.shape)b1 -= XX*np.dot(np.dot(w2,E)*A1,np.ones(train_m).reshape(-1,1))/train_m# 更新 w1w1 -= XX*np.dot(train_x.transpose(),(np.dot(w2,E)*A1).transpose())/train_m# 更新b2b2 -= XX*np.dot(E,np.ones(train_m).reshape(-1,1))/train_m# 更新 w2w2 -= XX*np.dot(A1,E.transpose())/train_m# 求测试集预测值部分Z1 = np.dot(w1.transpose(),test_x.transpose()) + np.dot(b1,np.ones(test_m).reshape(1,-1))# 激活函数是ReLU 计算A1 n*mA1 = ReLU(Z1)# 计算Z2 c*mZ2 = np.dot(w2.transpose(),A1) + np.dot(b2,np.ones(test_m).reshape(1,-1))# 输出层使用的是sigmoid 激活函数 ,预测值为 predict_ypredict_y = np.exp(Z2)/np.dot(np.ones(4*4).reshape(4,4),Z2)# 更新权重部分# 统计错误e = np.argmax(predict_y,0)-np.argmax(test_y,0)Errors[1].append(np.sum(e*e))# 绘图部分
print(min(Errors[0]),min(Errors[1]))
X = [i+1 for i in range(epoch)]
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
plt.plot(X,Errors[1],color='k',linestyle='dashed',label='测试集错误',linewidth=3)
plt.plot(X,Errors[0],color='#ec2d7a',linestyle='dashdot',label='训练集错误',linewidth=3)
plt.legend()
plt.title('多分类神经网络')
plt.tight_layout()
plt.show()资源地址
项目地址
gitee地址
总结
全文代码均手撸。
相关文章:

机器学习(监督学习)笔记
目录 总览笔记内容线性回归梯度下降特征缩放多输出线性回归 逻辑回归二分类与逻辑回归分类任务的性能指标(召回率,精度,F1分数等)支持向量机SVMK近邻朴素贝叶斯分类器朴素贝叶斯分类器进阶多分类逻辑回归二分类神经网络多分类神经…...
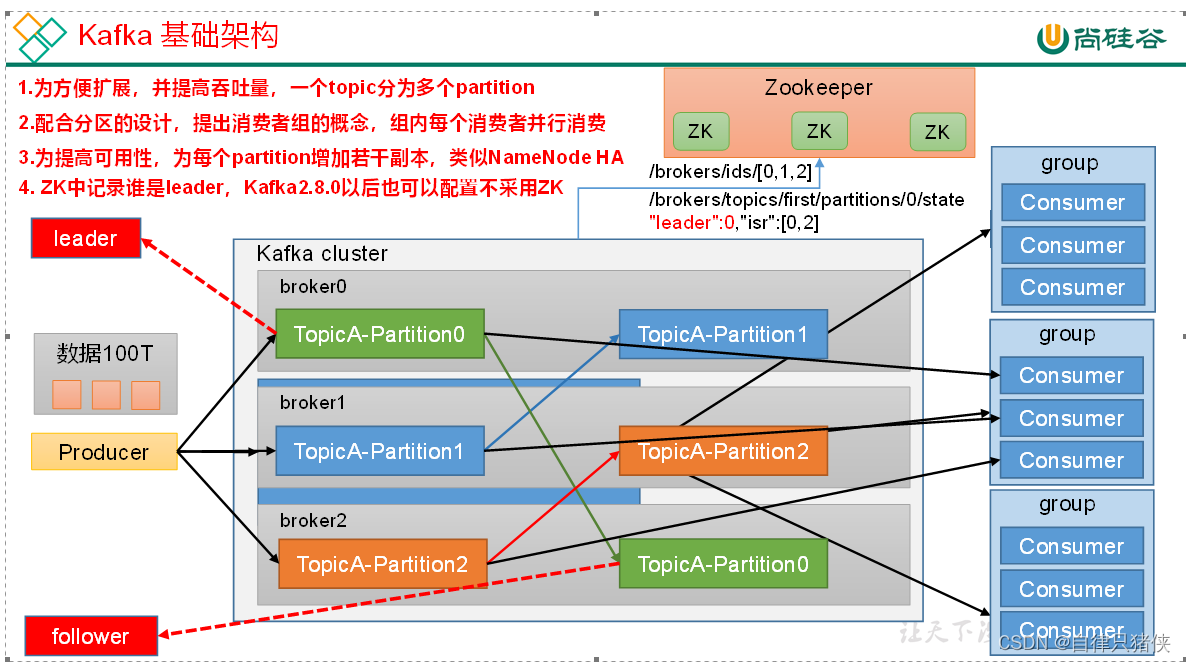
科普rabbitmq,rocketmq,kafka三者的架构比较
对比 架构对比 从架构可以看出三者有些类似,但是在细节上有很多不同。下面我们就从它们的各个组件,介绍它们: RabbitMQ,是一种开源的消息队列中间件。下面是RabbitMQ中与其相关的几个概念: 1.生产者(P…...
)
加密货币交易技巧——地利(二)
EMA指标 针对资金体量大的代币,做现货交易或低倍合约,可参考以下指标: 1.指标介绍:EMA,移动平均线指标,这里只分享中长线用法,非常实用且准确率超高 2.适用群体:适用于现货或低倍…...

服务网关Gateway_微服务中的应用
没有服务网关 问题: 地址太多安全性管理问题 为什么要使用服务网关 网关是微服务架构中不可或缺的部分。使用网关后,客户端和微服务之间的网络结构如下。 注意: 网关统一向外部系统(如访问者、服务)提供REST API。在Sp…...

2G大小的GPU对深度学习的加速效果如何?
训练数据情况 总共42776张224*224*3张图片 Found 42776 files belonging to 9 classes. Using 12833 files for training. 模型参数情况 Total params: 10,917,385 Trainable params: 10,860,745 Non-trainable params: 56,640 batch-size:12 GPU信息 NVIDIA GeForce GT 7…...

intel 一些偏门汇编指令总结
intel 汇编手册下载链接:https://www.intel.com/content/www/us/en/developer/articles/technical/intel-sdm.html LDS指令: 手册中可以找到 位于 3-588 根据手册内容猜测:lds r16 m16:16 的作用,是把位于 [m16:16] 内存地址的数…...

python 多个proto文件import引用时出现ModuleNotFoundError错误
问题描述 my_proto文件夹里有两个proto文件,book.proto想要引用person.proto文件中的Person,如下 book.proto syntax "proto2";import "person.proto"; // 导入person.proto文件message Book {optional string name 1;optional …...
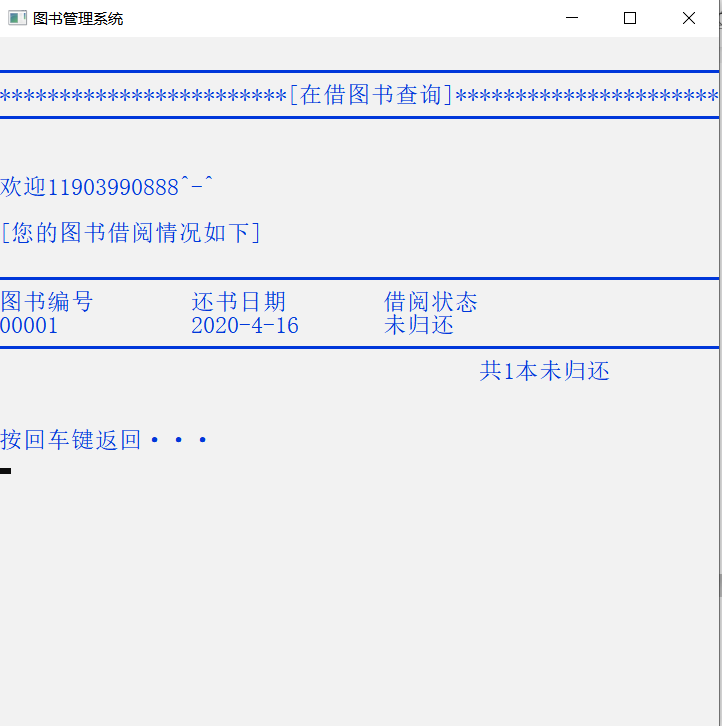
C语言图书管理系统
一、 系统概述 图书管理系统是一个用C语言编写的软件系统,旨在帮助图书馆或图书机构管理其图书馆藏书和读者信息。该系统提供了一套完整的功能,包括图书录入、借阅管理、归还管理、读者管理、图书查询、统计报表等。 二、 系统功能 2.1 图书录入 管理…...

归并排序及其非递归实现
个人主页:Lei宝啊 愿所有美好如期而遇 目录 归并排序递归实现 归并排序非递归实现 归并排序递归实现 图示: 代码: 先分再归并,像是后序一般。 //归并排序 void MergeSort(int* arr, int left, int right) {int* temp (int…...
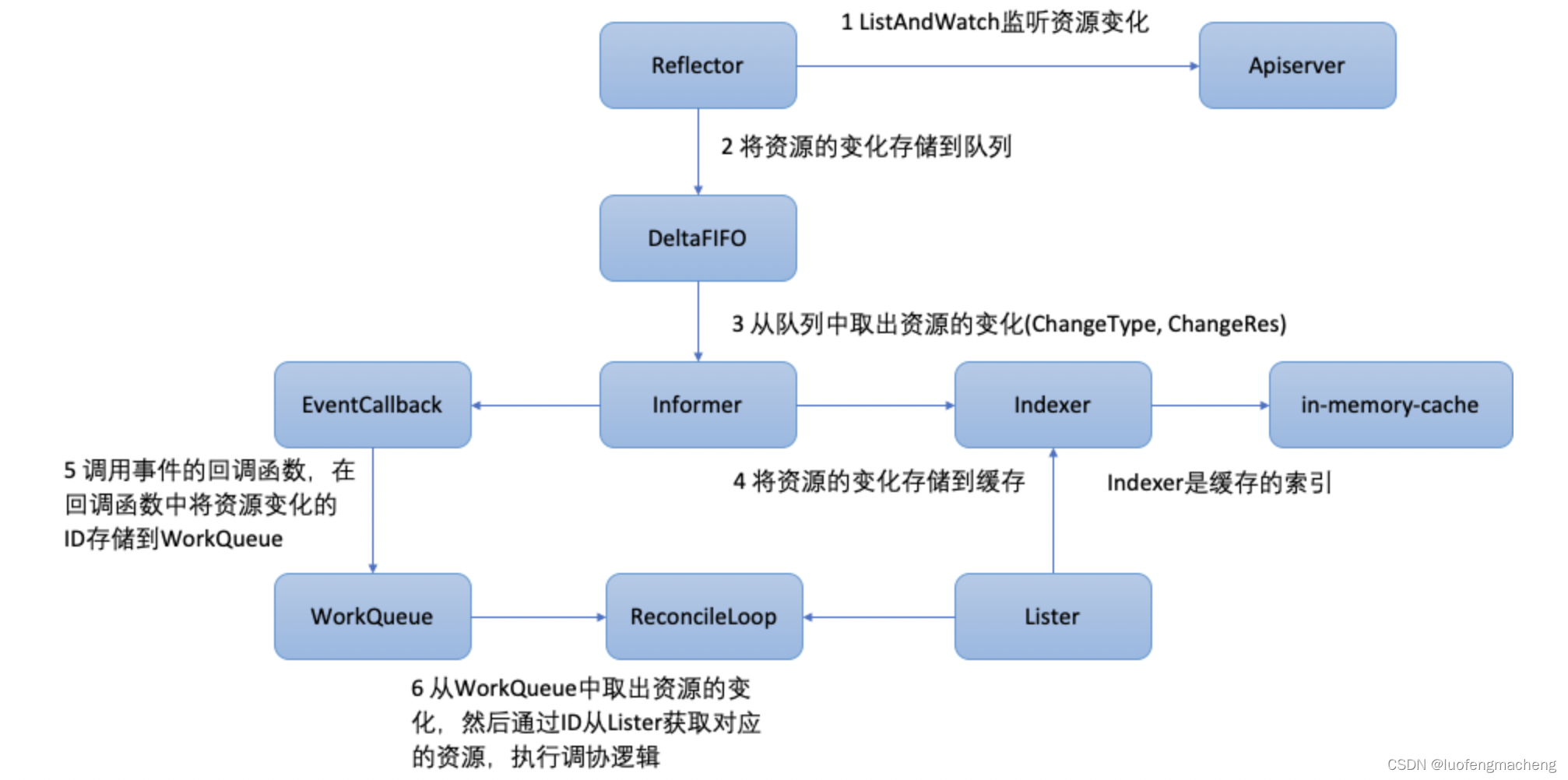
【kubernetes】kubernetes中的Controller
1 什么是Controller? kubernetes采用了声明式API,与声明式API相对应的是命令式API: 声明式API:用户只需要告诉期望达到的结果,系统自动去完成用户的期望命令式API:用户需要关注过程,通过命令一…...

RabbitMQ-死信队列
接上文 RabbitMQ-java使用消息队列 1 死信队列简介 死信队列模式实际上本质是一个死信交换机绑定的死信队列,当正常队列的消息被判定为死信时,会被发送到对应的死信交换机,然后再通过交换机发送到死信队列中,死信队列也有对应的消…...

ElasticSearch - 基于 DSL 、JavaRestClient 实现数据聚合
目录 一、数据聚合 1.1、基本概念 1.1.1、聚合分类 1.1.2、特点 1.2、DSL 实现 Bucket 聚合 1.2.1、Bucket 聚合基础语法 1.2.2、Bucket 聚合结果排序 1.2.3、Bucket 聚合限定范围 1.3、DSL 实现 Metrics 聚合 1.4、基于 JavaRestClient 实现聚合 1.4.1、组装请求 …...
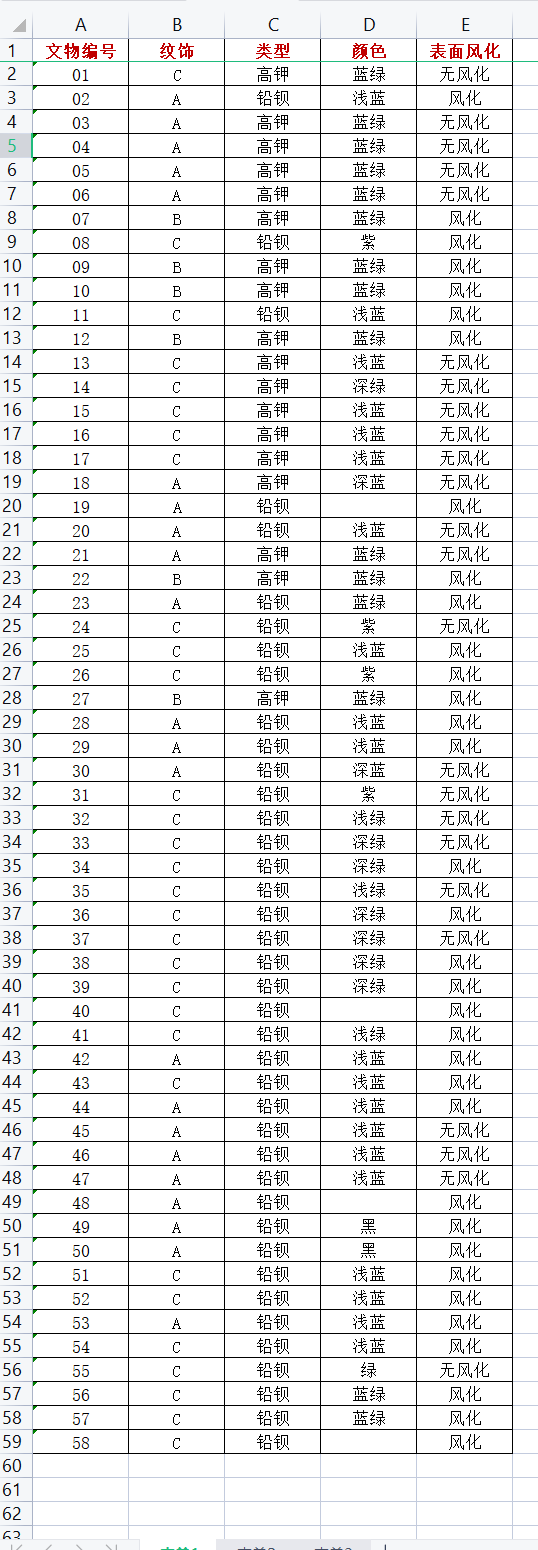
什么是数学建模(mooc笔记)
什么是数学建模 前提:我们数学建模国赛计划选择C题,故希望老师的教学中侧重与C题相关性大的模型及其思想进行培训。之后的学习内容中希望涉及以下知识点: logistic回归相关知识点。如:用法、适用、限制范围等。精学数学建模中常…...
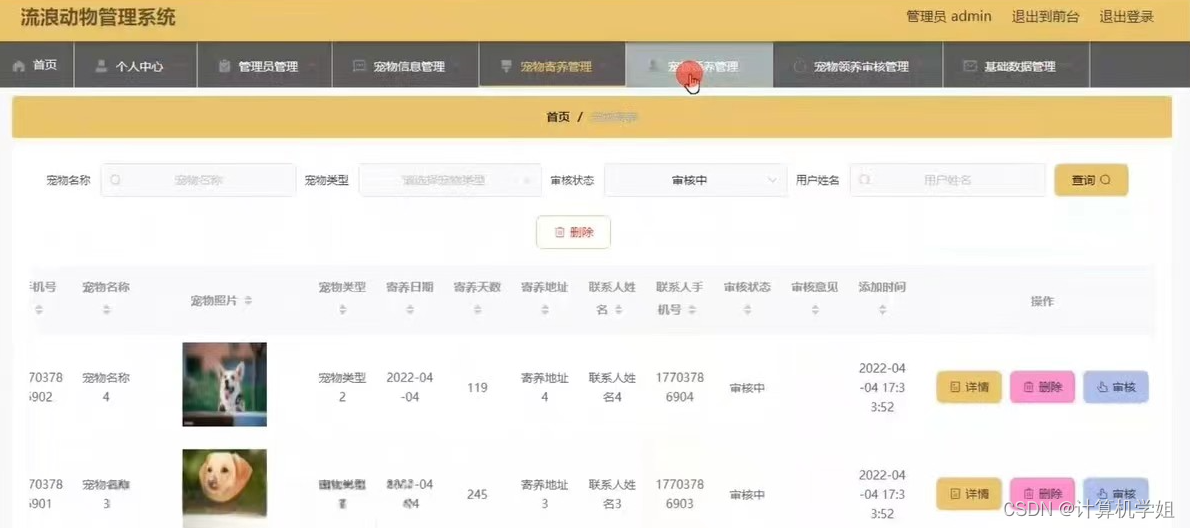
基于SpringBoot的流浪动物管理系
基于SpringBoot的流浪动物管理系的设计与实现,前后端分离 开发语言:Java数据库:MySQL技术:SpringBootMyBatisVue工具:IDEA/Ecilpse、Navicat、Maven 系统展示 首页 后台登陆界面 管理员界面 摘要 基于Spring Boot的…...
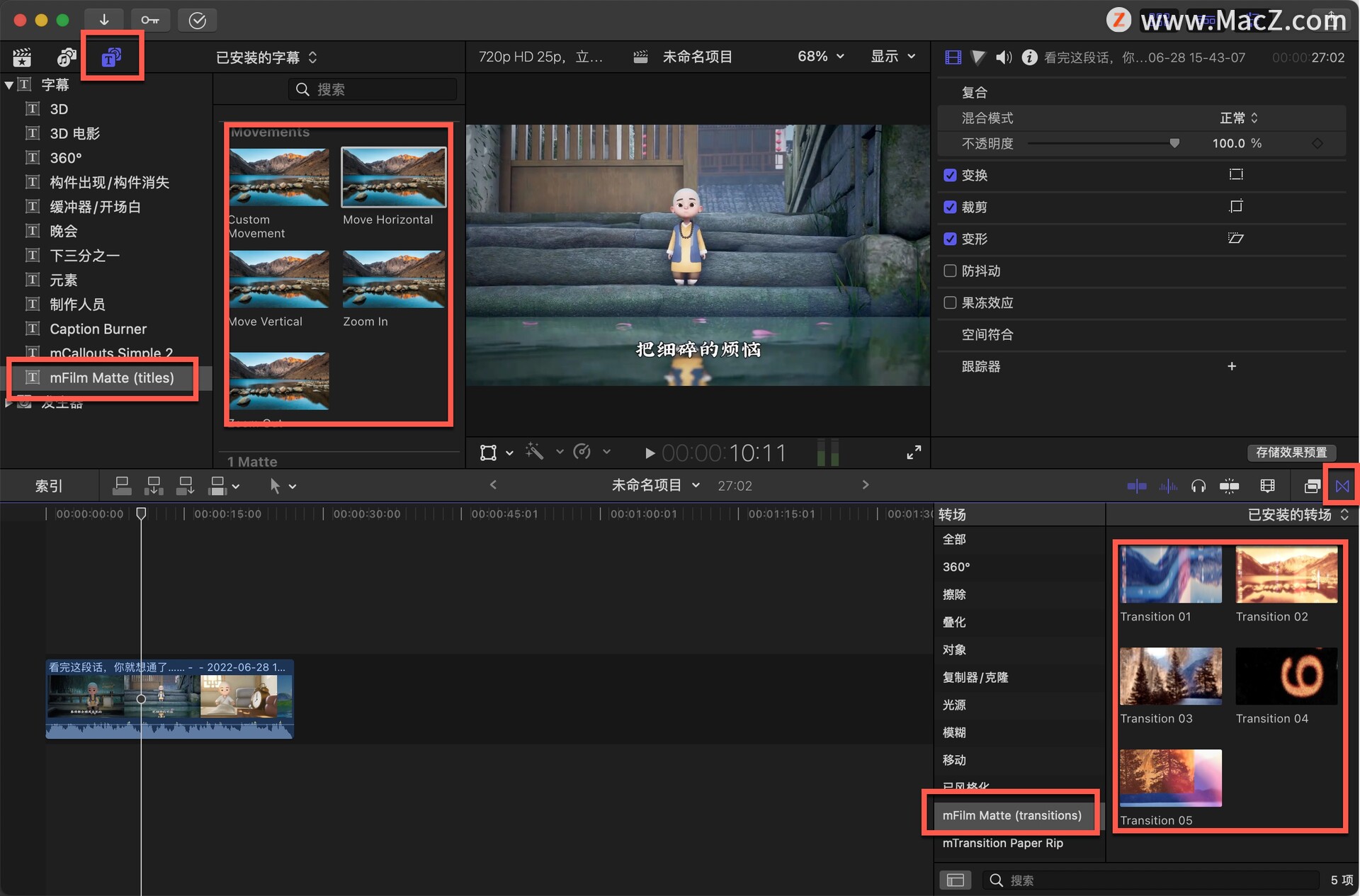
fcpx插件:82种复古电影胶卷框架和效果mFilm Matte
无论您是在制作音乐剪辑、私人假期视频还是大型广告活动,这个专业的插件都将帮助您为您的镜头赋予真正的电影角色。 复古效果在任何视频中都能立即识别出来,增添了感伤的复古氛围,并使镜头更具说服力。使用 mFilm Matte 轻松实现这些特征&…...
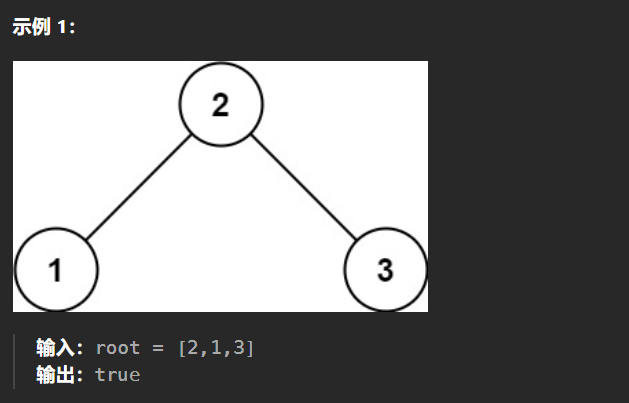
【LeetCode热题100】--98.验证二叉搜索树
98.验证二叉搜索树 给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。 有效 二叉搜索树定义如下: 节点的左子树只包含 小于 当前节点的数。节点的右子树只包含 大于 当前节点的数。所有左子树和右子树自身必须也是二叉搜索树。 由于二…...

wxpython:wx.grid 表格显示 Excel xlsx文件
pip install xlrd xlrd-1.2.0-py2.py3-none-any.whl (103 kB) 摘要: Library for developers to extract data from Microsoft Excel (tm) spreadsheet files pip install wxpython4.2 wxPython-4.2.0-cp37-cp37m-win_amd64.whl (18.0 MB) Successfully installed wxpython-4.…...

事件循环机制
eventLoop 事件循环(Event Loop)是用于管理和调度异步任务执行的一种机制,通常在浏览器中,也在其他 JavaScript 运行环境中存在。事件循环确保 JavaScript 单线程的执行模型下能够处理非阻塞的异步任务,以避免程序阻塞…...

苹果曾考虑基于定位控制AirPods Pro自适应音频
在一次最近的采访中,苹果公司的高管Ron Huang和Eric Treski透露,他们在开发AirPods Pro自适应音频功能时,曾考虑使用GPS信号来控制音频级别。这个有趣的细节打破了我们对AirPods Pro的固有认知,让我们对苹果的创新思维有了更深的…...

【代码阅读笔记】yolov5 rknn模型部署
一、main函数思路 二、值得学习的地方 1、关注yolov5检测流程 2、其中几个重要的结构体 typedef struct {int left;int right;int top;int bottom; } YOLOV5_BOX_RECT; // box坐标信息typedef struct {char name[YOLOV5_NAME_MAX_SIZE];int class_index;YOLOV5_BOX_RECT box…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

Java + Spring Boot + Mybatis 实现批量插入
在 Java 中使用 Spring Boot 和 MyBatis 实现批量插入可以通过以下步骤完成。这里提供两种常用方法:使用 MyBatis 的 <foreach> 标签和批处理模式(ExecutorType.BATCH)。 方法一:使用 XML 的 <foreach> 标签ÿ…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...

高考志愿填报管理系统---开发介绍
高考志愿填报管理系统是一款专为教育机构、学校和教师设计的学生信息管理和志愿填报辅助平台。系统基于Django框架开发,采用现代化的Web技术,为教育工作者提供高效、安全、便捷的学生管理解决方案。 ## 📋 系统概述 ### 🎯 系统定…...

绕过 Xcode?使用 Appuploader和主流工具实现 iOS 上架自动化
iOS 应用的发布流程一直是开发链路中最“苹果味”的环节:强依赖 Xcode、必须使用 macOS、各种证书和描述文件配置……对很多跨平台开发者来说,这一套流程并不友好。 特别是当你的项目主要在 Windows 或 Linux 下开发(例如 Flutter、React Na…...

规则与人性的天平——由高考迟到事件引发的思考
当那位身着校服的考生在考场关闭1分钟后狂奔而至,他涨红的脸上写满绝望。铁门内秒针划过的弧度,成为改变人生的残酷抛物线。家长声嘶力竭的哀求与考务人员机械的"这是规定",构成当代中国教育最尖锐的隐喻。 一、刚性规则的必要性 …...
