考研复试机试 | c++ | 王道复试班
目录
- n的阶乘 (清华上机)
- 题目描述
- 代码
- 汉诺塔问题
- 题目:
- 代码:
- Fibonacci数列 (上交复试)
- 题目
- 代码:
- 二叉树:
- 题目:
- 代码:
n的阶乘 (清华上机)
不敢相信这是清华上机
题目描述
输入一个整数n,输出n的阶乘
代码
递归写法:
#include <cstido>
Factorial(int n){if(n==1){return 1;}else{return Factorial(n-1)*n;}
} int main(){int n;scanf("%d",&n);printf("%d\n",Factorial(n));
}
循环写法
int main(){int n;int sum = 1;scanf("%d",&n);for(int i=1;i<=n;i++){sum = sum*i;}printf("%d",sum);
}
汉诺塔问题
题目:
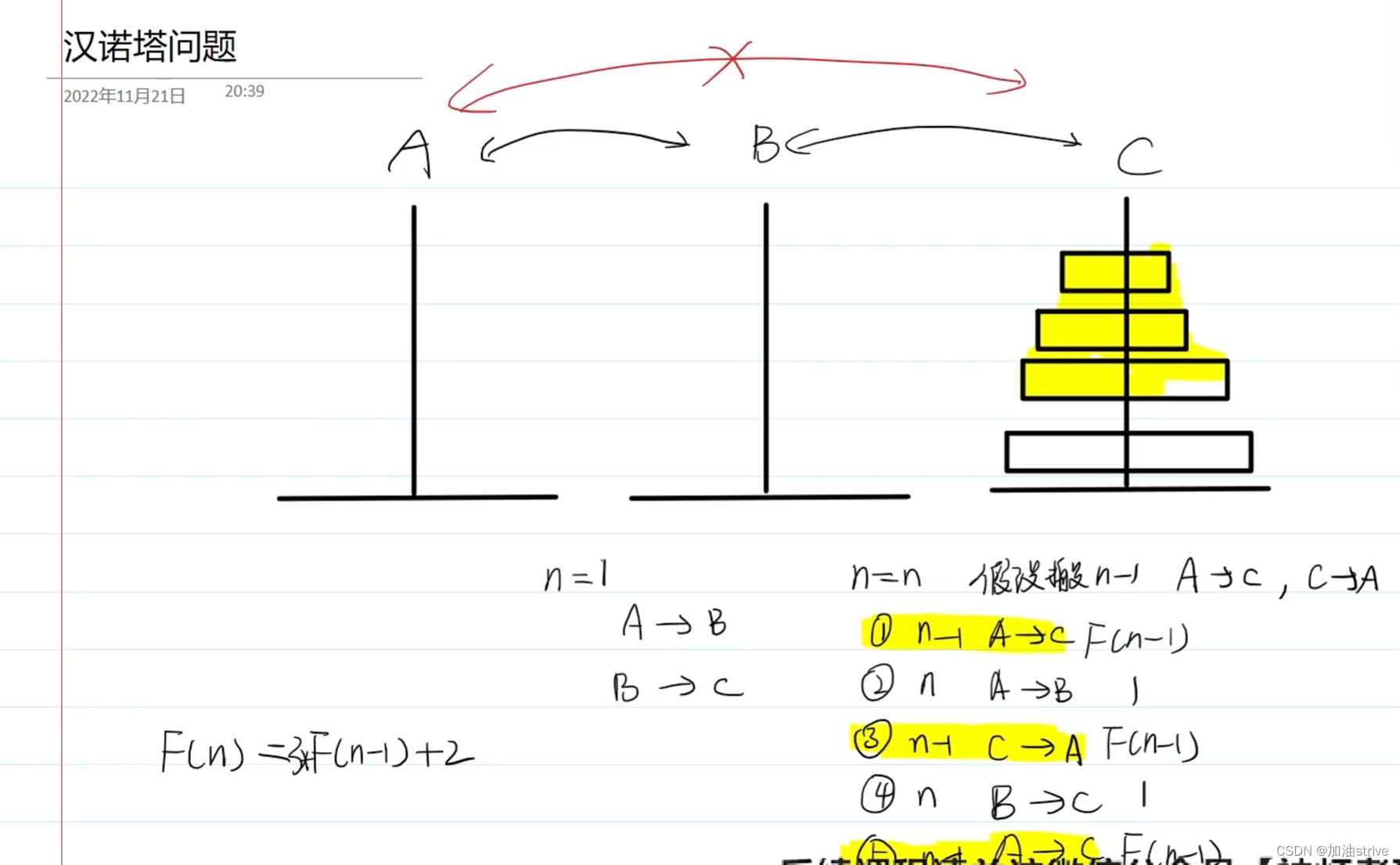
约19世纪末,在欧州的商店中出售一种智力玩具,在一块铜板上有三根杆,最左边的杆上自上而下、由小到大顺序串着由64个圆盘构成的塔。目的是将最左边杆上的盘全部移到右边的杆上,条件是一次只能移动一个盘,且不允许大盘放在小盘的上面。
现在我们改变游戏的玩法,不允许直接从最左(右)边移到最右(左)边(每次移动一定是移到中间杆或从中间移出),也不允许大盘放到下盘的上面。
Daisy已经做过原来的汉诺塔问题和汉诺塔II,但碰到这个问题时,她想了很久都不能解决,现在请你帮助她。现在有N个圆盘,她至少多少次移动才能把这些圆盘从最左边移到最右边?
Input
包含多组数据,每次输入一个N值(1<=N=35)。
Output
对于每组数据,输出移动最小的次数。
Sample Input
1
3
12
Sample Output
2
26
531440
代码:
#include <cstdio>
//现在有N个圆盘,她至少多少次移动才能把这些圆盘从最左边移到最右边?
long long hanoi(int n){if(n==1) return 2;else return 3*hanoi(n-1)+2;
}int main(){int n;while(scanf("%d",&n)!=EOF){printf("%lld",hanoi(n));}
}
Fibonacci数列 (上交复试)
题目
描述
The Fibonacci Numbers{0,1,1,2,3,5,8,13,21,34,55…} are defined by the recurrence: F0=0 F1=1 Fn=Fn-1+Fn-2,n>=2 Write a program to calculate the Fibonacci Numbers.
输入描述:
Each case contains a number n and you are expected to calculate Fn.(0<=n<=30) 。
输出描述:
For each case, print a number Fn on a separate line,which means the nth Fibonacci Number.
示例1
输入:
1
输出:
1
代码:
#include <cstdio>int Fibonacci(int n){if(n==1){return 1;}else if(n==0){return 0;}else{return Fibonacci(n-1)+Fibonacci(n-2);}
}//斐波那契数列
int main(){int n;while(scanf("%d",&n)!=EOF){printf("%d\n",Fibonacci(n));}
}
二叉树:
题目:
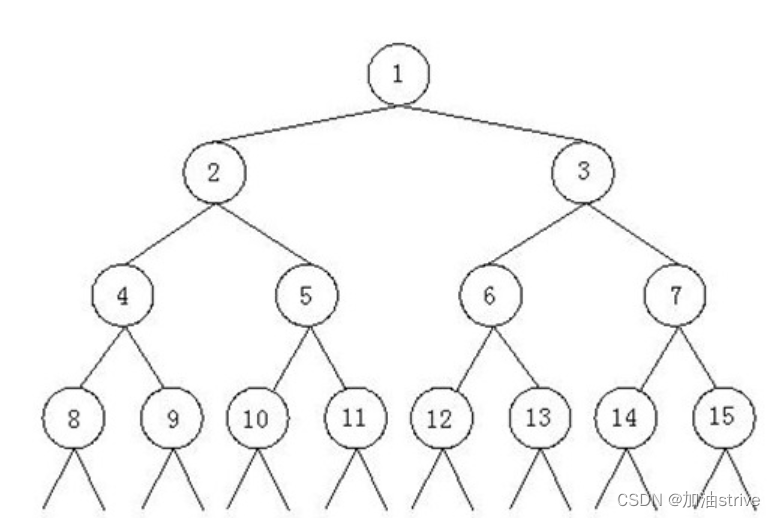
如上所示,由正整数1,2,3……组成了一颗特殊二叉树。我们已知这个二叉树的最后一个结点是n。现在的问题是,结点m所在的子树中一共包括多少个结点。 比如,n = 12,m = 3那么上图中的结点13,14,15以及后面的结点都是不存在的,结点m所在子树中包括的结点有3,6,7,12,因此结点m的所在子树中共有4个结点。
输入描述:
输入数据包括多行,每行给出一组测试数据,包括两个整数m,n (1 <= m <= n <= 1000000000)。
输出描述:
对于每一组测试数据,输出一行,该行包含一个整数,给出结点m所在子树中包括的结点的数目。
示例1
输入:
3 12
0 0
输出:
4
分析:
- 首先:该树是一颗完全二叉树,若root节点是数字p,那么左节点是数字2p
右节点是数字2p+1; - 如果子树存在 tree(m) = tree(2m)+tree(2m+1);
也就是说,该子树的节点数量= 左子树节点数量+右子树节点数量 +1(根节点) - 如果子树根不存在,则tree(m)为0;
代码:
#include <cstdio>// m表示当前节点 n表示节点总数
int tree(int m,int n){// 如果当前节点的序号大于节点总数 if(m > n){return 0;}else{return 1+tree(2*m,n)+tree(2*m+1,n);}
}int main(){int m,n;while(scanf("%d%d",&m,&n)!=EOF){if(m==0) break;printf("%d\n",tree(m,n));}
}相关文章:

考研复试机试 | c++ | 王道复试班
目录n的阶乘 (清华上机)题目描述代码汉诺塔问题题目:代码:Fibonacci数列 (上交复试)题目代码:二叉树:题目:代码:n的阶乘 (清华上机) …...

js闭包简单理解
js里面的闭包是一个难点也是它的一个特色,是我们必须掌握的js高级特性,那么什么是闭包呢?它又有什么作用呢? 1,提到闭包我们这里先讲解一下js作用域的问题 js的作用域分两种,全局和局部,基于我…...

「JVM 编译优化」编译器优化技术
后端编译(即时编译、提前编译)的目标时将字节码翻译成本地机器码,而难点是输出优化质量较高的机器码; 文章目录1. 优化技术概览2. 方法内联(Inlining)3. 逃逸分析(Escape Analysis)4…...
回溯问题(子集型回溯、组合型回溯、排列型回溯)【零神基础精讲】
来源0x3f:https://space.bilibili.com/206214 回溯分为【子集型回溯】【组合型回溯】【排列型回溯】 文章目录回溯基本概念[17. 电话号码的字母组合](https://leetcode.cn/problems/letter-combinations-of-a-phone-number/)子集型回溯(分割问题也可以看…...

源代码配置安装Apache
源代码配置安装Apache 📒博客主页: 微笑的段嘉许博客主页 💻微信公众号:微笑的段嘉许 🎉欢迎关注🔎点赞👍收藏⭐留言📝 📌本文由微笑的段嘉许原创! …...

css水平垂直居中各种方法实现方式
不定宽高水平垂直居中? 面试题回答方式: 通过display:flex;justify-content:center; align-items:center;就可以让子元素不定宽高水平垂直居中 也可以父display:flex;,子设置一个margin&#…...
PowerShell Install java 13
java 前言 Java具有大部分编程语言所共有的一些特征,被特意设计用于互联网的分布式环境。Java具有类似于C语言的形式和感觉,但它要比C语言更易于使用,而且在编程时彻底采用了一种以对象为导向的方式。 java download javadownloadPowersh…...
Python的PyQt框架的使用(汇总)
Python的PyQt框架的使用一、前言二、安装PyQt三、使用第三方开发工具四 、创建主窗体五、常用控件篇1.QLineEdit 文本框2.QPushButton按钮控件3.QRadioButton 单选按钮六、布局管理篇1.通过布局管理器布局2.绝对布局七、信号与槽的关联1.编辑信号/槽2.信号/槽编辑器八、资源文件…...

力扣热题100Day05:15.三数之和,17. 电话号码的字母组合,19. 删除链表的倒数第 N 个结点
15.三数之和 题目链接:15. 三数之和 - 力扣(Leetcode) 思路: (1)双指针,在外层for循环里加入两个指针,left和right (2)排序:为了更好地进行去…...

探索开源:获取完整的 GitHub 社区数据集
本篇文章聊聊 GitHub 开放数据集的获取和整理,分享一些数据整理的细节技巧,以及一些相对粗浅的数据背后的事情。 写在前面 分析 GitHub 上的项目和开发者获取是深入、真实的了解开源世界演进的方法之一。 在 GHArchive 项目中,我们能够看到…...
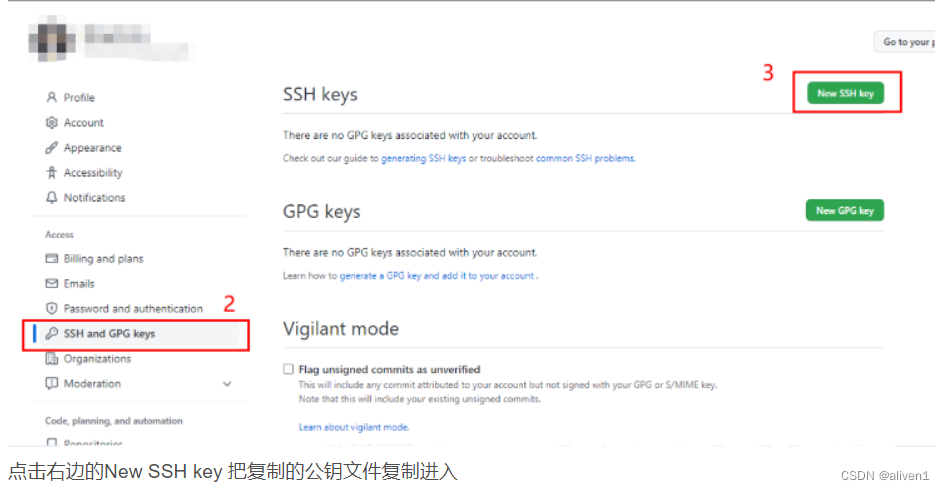
github ssh密钥配置,克隆远程仓库
GitHub的SSH配置 在往github上push项目的时候,如果走https的方式,每次都需要输入账号密码,非常麻烦。而采用ssh的方式,就不再需要输入,只需要在github自己账号下配置一个ssh key即可! 很多朋友在用github管…...

突破年薪百万难关!吃透这套Java真题合集
前言我相信大多 Java 开发的程序员或多或少经历过BAT一些大厂的面试,也清楚一线互联网大厂 Java 面试是有一定难度的,小编经历过多次面试,有满意的也有备受打击的。因此呢小编想把自己这么多次面试经历以及近期的面试真题来个汇总分析&#x…...
[黑马程序员SSM框架教程] Spring-11-setter注入
思考:向一个类中传递数据要几种? set方法构造方法 思考:依赖注入描述了在容器中建立bean与bean之间依赖关系的过程,如果bean运行需要数字或字符呢 引用类型简单类型(基本数据类型和字符串) 注入方式&#x…...
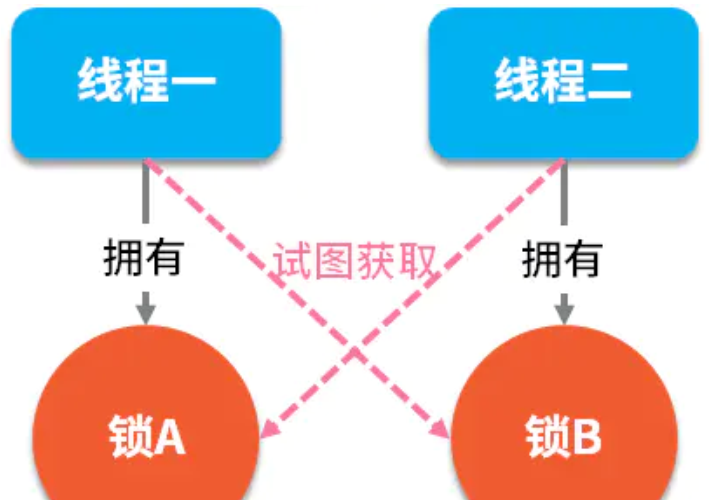
Java多线程(一)--多线程基础知识
1. 为什么要使用并发编程提升多核CPU的利用率:一般来说一台主机上的会有多个CPU核心,我们可以创建多个线程,理论上讲操作系统可以将多个线程分配给不同的CPU去执行,每个CPU执行一个线程,这样就提高了CPU的使用效率&…...

AutoDock, AutoDock-vina等对接工具安装
AutoDock, AutoDock-vina等对接工具安装 AutoDock-GPU安装 下载地址: https://autodock.scripps.edu/downloads/ 将压缩包传送至安装目录中,并解压到当前路径 unzip AutoDock-GPU-develop.zip 找到服务器的cuda的路径,cuda的路径一般默认…...
)
MySQL常见面试题(2023年最新)
目录1.char和varchar的区别2.数据库的三大范式3.索引是什么4.索引的优点和缺点5.索引怎么设计(优化)6.索引的类型7.索引的数据类型8.索引为什么使用树结构9.二叉查找树、B树、B树10.为什么使用B树不用B树11.最左匹配原则12.MylSAM和InnoDB的区别13.什么是事务14.事务的四大特性…...

C# 泛型详解
C# 泛型详解1、泛型概述2、定义泛型3、泛型的特性4、泛型委托5、泛型的优点在 C# 中,泛型(Generic)是一种规范,它允许我们使用占位符来定义类和方法,编译器会在编译时将这些占位符替换为指定的类型,利用泛型…...

数据仓库相关术语
数据仓库数据集市事实维度级别数据清洗数据采集数据转换联机分析处理(OLAP OnlineAnalytical Processing )切片切块星型模式雪花模式粒度度量度量值口径指标 原子指标:派生指标衍生指标标签自然键持久键代理键退化维度下钻上卷T0与T1数据挖掘数据科学家总线架构总线…...

【IDEA】常用快捷键
代码补全 快捷键说明sout快速输出System.out.println();psvm快速输出public static void main(String[] args) {}Ctrl Alt Space代码补全 编辑类 快捷键说明Shift Enter向下键入一行,并将光标移到下一行的开头Ctrl Alt Enter当前行上方生成空行,并…...

【调试】sysRq按键使用方法
SysRq键简介 SysRq键是一个魔术案件,只要在内核没有完全卡死的情况下,内核都会相应SysRq 键的输入,使用这些组合键都可以搜集包括系统内存使用、CPU任务处理、进程运行状态等系统运行信息。 配置 内核配置选项中要使能CONFIG_MAGIC_SYSRQ选…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

ios苹果系统,js 滑动屏幕、锚定无效
现象:window.addEventListener监听touch无效,划不动屏幕,但是代码逻辑都有执行到。 scrollIntoView也无效。 原因:这是因为 iOS 的触摸事件处理机制和 touch-action: none 的设置有关。ios有太多得交互动作,从而会影响…...

嵌入式常见 CPU 架构
架构类型架构厂商芯片厂商典型芯片特点与应用场景PICRISC (8/16 位)MicrochipMicrochipPIC16F877A、PIC18F4550简化指令集,单周期执行;低功耗、CIP 独立外设;用于家电、小电机控制、安防面板等嵌入式场景8051CISC (8 位)Intel(原始…...

Qt 事件处理中 return 的深入解析
Qt 事件处理中 return 的深入解析 在 Qt 事件处理中,return 语句的使用是另一个关键概念,它与 event->accept()/event->ignore() 密切相关但作用不同。让我们详细分析一下它们之间的关系和工作原理。 核心区别:不同层级的事件处理 方…...

9-Oracle 23 ai Vector Search 特性 知识准备
很多小伙伴是不是参加了 免费认证课程(限时至2025/5/15) Oracle AI Vector Search 1Z0-184-25考试,都顺利拿到certified了没。 各行各业的AI 大模型的到来,传统的数据库中的SQL还能不能打,结构化和非结构的话数据如何和…...

DiscuzX3.5发帖json api
参考文章:PHP实现独立Discuz站外发帖(直连操作数据库)_discuz 发帖api-CSDN博客 简单改造了一下,适配我自己的需求 有一个站点存在多个采集站,我想通过主站拿标题,采集站拿内容 使用到的sql如下 CREATE TABLE pre_forum_post_…...
