存在负权边的单源最短路径的原理和C++实现
负权图

此图用朴素迪氏或堆优化迪氏都会出错,floyd可以处理。
负环图
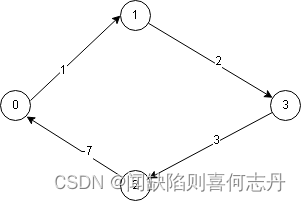
但floyd无法处理负权环,最短距离是无穷小。在环上不断循环。
经过k条边的最短距离(可能有负权变)
贝尔曼福特算法(bellman_ford)就是解决此问题的。
原理
循环k次,循环第i次时,m_vDis表示各点最多经过i-1条边的最短距离;vDis表示各点最多经过i条边的最短距离。
核心代码
template<const int INF=1000*1000*1000>
class CBellMan
{
public:
CBellMan(int n, const vector<vector<int>>& edges,int s , int k )
{
m_vDis.assign(n, INF);
m_vDis[s] = 0;
for (int i = 1; i <= k; i++)
{
vector<int> curDis = m_vDis;
for (const auto& v : edges)
{
if (INF == m_vDis[v[0]])
{
continue;
}
curDis[v[1]] = min(curDis[v[1]], m_vDis[v[0]] + v[2]);
}
m_vDis.swap(curDis);
}
}
vector<int> m_vDis;
};
测试样例
#include <vector>
#include<assert.h>
using namespace std;
int main()
{
const int INF = 1000 * 1000 * 1000;
vector<vector<int>> edges = { {0,1,1},{1,2,2},{2,3,3},{3,0,-7} };
vector<vector<int>> results = { {0,INF,INF,INF},{0,1,INF,INF},{0,1,3,INF},{0,1,3,6},{-1,1,3,6},{-1,0,3,6},{-1,0,2,6},{-1,0,2,5},{-2,0,2,5} };
for (int i = 0; i < results.size(); i++)
{
CBellMan<> bm(4, edges, 0, i);
for (int j = 0; j < 4; j++)
{
assert(bm.m_vDis[j] == results[i][j]);
}
}
}
最短路径
最短路径就是经过“点数-1”条边的最短路径。如果没环,这些边可以到达任意点。如果有正权环和0权环,则拿掉这个环。如果负权环,则最小距离是无穷小。下面来检测负权环。循环“点数-1”后,再循环一次,如果有点的最短距离变小,则一定有负权环;没负权环,不会变短。如果有负权环,则再循环一次,一定有点(任意负权环的负权边的终点)距离变短。假定此点是e,拿掉负权环上所有的边后,源点到e的最短路径为Path。不拿掉负权环,则e的最短路径为:Path+此负权环。
核心代码
template<const int INF=1000*1000*1000>
class CBellMan
{
public:
CBellMan(int n, const vector<vector<int>>& edges,int s , int k )
{
m_vDis.assign(n, INF);
m_vDis[s] = 0;
for (int i = 1; i <= k; i++)
{
vector<int> curDis = m_vDis;
Do(edges, curDis);
m_vDis.swap(curDis);
}
}
bool Check(const vector<vector<int>>& edges)
{
vector<int> curDis = m_vDis;
Do(edges, curDis);
for (int i = 0; i < curDis.size(); i++)
{
if (m_vDis[i] != curDis[i])
{
return true;
}
}
return false;
}
void Do(const std::vector<std::vector<int>>& edges, std::vector<int>& curDis)
{
for (const auto& v : edges)
{
if (INF == m_vDis[v[0]])
{
continue;
}
curDis[v[1]] = min(curDis[v[1]], m_vDis[v[0]] + v[2]);
}
}
vector<int> m_vDis;
};
测试样例
#include <vector>
#include<assert.h>
#include "BellMan.h"
using namespace std;
void Test1()
{
const int INF = 1000 * 1000 * 1000;
vector<vector<int>> edges = { { 0,1,1 },{ 1,2,2 },{ 2,3,3 },{ 3,0,-7 } };
vector<vector<int>> results = { { 0,INF,INF,INF },{ 0,1,INF,INF },{ 0,1,3,INF },{ 0,1,3,6 },{ -1,1,3,6 },{ -1,0,3,6 },{ -1,0,2,6 },{ -1,0,2,5 },{ -2,0,2,5 } };
for (int i = 0; i < results.size(); i++)
{
CBellMan<> bm(4, edges, 0, i);
for (int j = 0; j < 4; j++)
{
assert(bm.m_vDis[j] == results[i][j]);
}
}
}
void Test2()
{
const int INF = 1000 * 1000 * 1000;
vector<vector<int>> edges = { { 0,1,1 },{ 1,2,2 },{ 2,3,3 },{ 3,0,-7 } };
vector<int> results = { false,false,true };
for (int i = 0; i < 3; i++)
{
edges[3][2] = -5 - i;
CBellMan<> bm(4, edges, 0, 3);
assert(results[i] == bm.Check(edges));
}
}
int main()
{
Test1();
Test2();
}
其它
测试环境
win7 VS2019 C++17
相关下载
源码及测试用例:
https://download.csdn.net/download/he_zhidan/88393784
doc版文档,排版好
https://download.csdn.net/download/he_zhidan/88348653
相关文章:

存在负权边的单源最短路径的原理和C++实现
负权图 此图用朴素迪氏或堆优化迪氏都会出错,floyd可以处理。 负环图 但floyd无法处理负权环,最短距离是无穷小。在环上不断循环。 经过k条边的最短距离(可能有负权变) 贝尔曼福特算法(bellman_ford)就是解决此问题的。 原理 …...
15-自动化测试——理论知识
目录 1.什么是自动化测试? 2.常见的自动化测试分类 2.1.单元测试(Java、Python) 2.2.接口测试(Java、Python) 2.3.UI测试(移动端、网站) 3.如何实施自动化测试? 4.自动化测试…...
学信息系统项目管理师第4版系列17_干系人管理
1. 项目经理和团队管理干系人的能力决定着项目的成败 2. 干系人满意度应作为项目目标加以识别和管理 3. 发展趋势和新兴实践 3.1. 识别所有干系人,而非在限定范围内 3.2. 确保所有团队成员都涉及引导干系人参与的活 3.3. 定期审查干系人群体,可与单…...

专业PDF编辑阅读工具PDF Expert mac中文特点介绍
PDF Expert mac是一款专业的PDF编辑和阅读工具。它可以帮助用户在Mac、iPad和iPhone等设备上查看、注释、编辑、填写和签署PDF文档。 PDF Expert mac软件特点 PDF编辑:PDF Expert提供了丰富的PDF编辑功能,包括添加、删除、移动、旋转、缩放、裁剪等操作…...
处理机调度的概念,层次联系以及七状态模型
1.基本概念 当有一堆任务要处理,但由于资源有限,这些事情没法同时处理。 这就需要确定某种规则来决定处理这些任务的顺序,这就是“调度”研究的问题。 2. 三个层次 1.高级调度(作业调度) 高级调度(作业…...
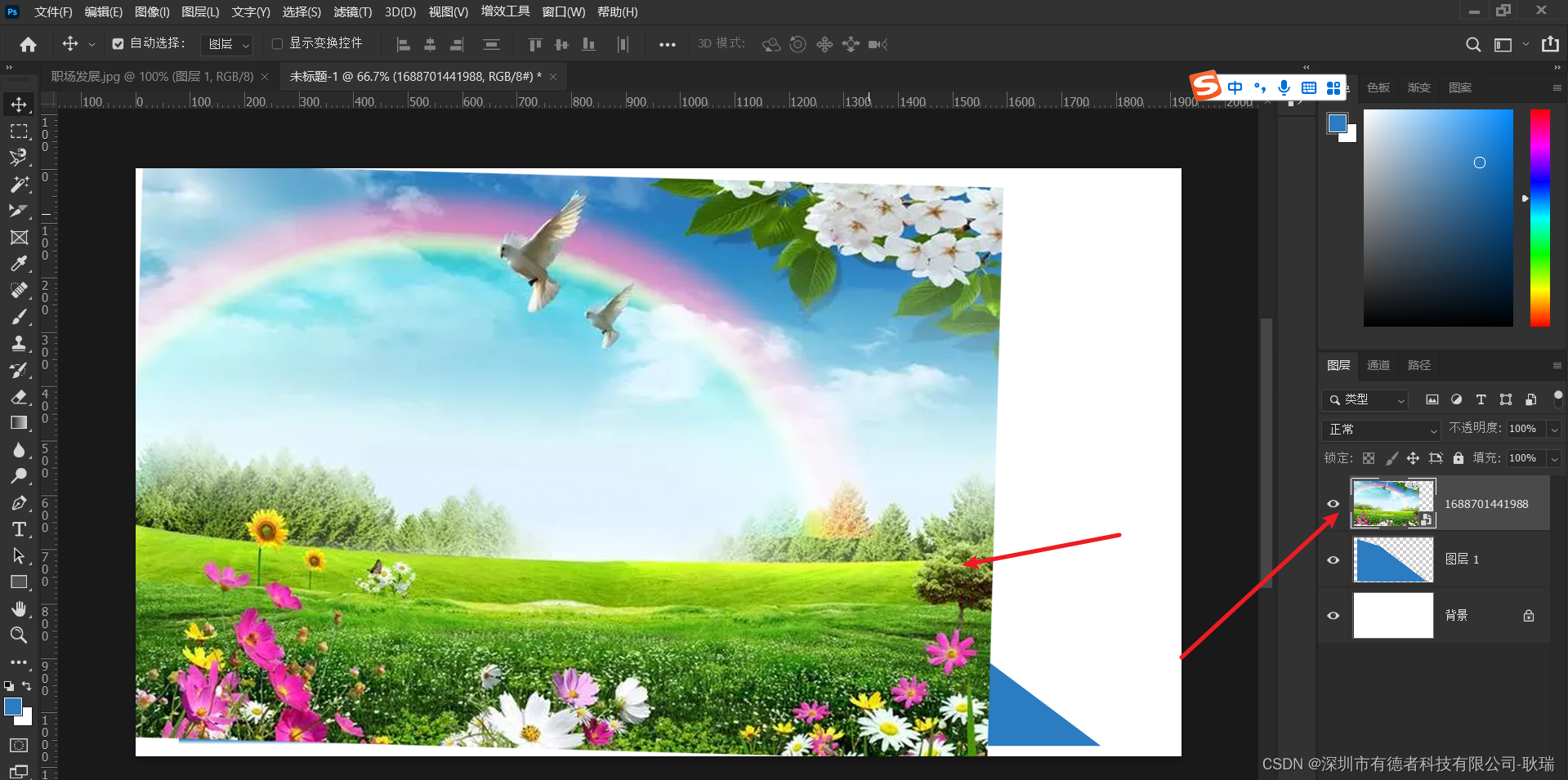
PS 图层剪贴蒙版使用方法
好 我们先打开PS软件 后面我们需要接触图框工具 在学习图框工具之前 先要掌握剪贴蒙版 这里 我们先点击左上角文件 然后选择新建 我们先新建一个画布出来 然后 我们点击 箭头指向处 新建一个空白图层 点击之后 会就多出一个空白图层 我们在这里 找到 矩形选框工具 然后 …...

总结1008
今日有些小摆烂,在家学习的日子,确实感觉不如在学校好,无论是在时间上,还是在效率上。在家复习效果因人而异吧,都到这个关键阶段了,可不能掉链子啊,明天势必要拿出100%的状态,心静不…...

软件工程从理论到实践客观题汇总(头歌第九章至第十七章)
九、软件体系结构设计 1、软件体系结构设计概述 2、软件体系结构模型的表示方法 3、软件体系结构设计过程 4、设计初步的软件体系结构 5、重用已有软件资源 6、精化软件体系结构 7、设计软件部署模型 8、文档化和评审软件体系结构设计 十、软件用户界面设计 1、用户界面设计概…...
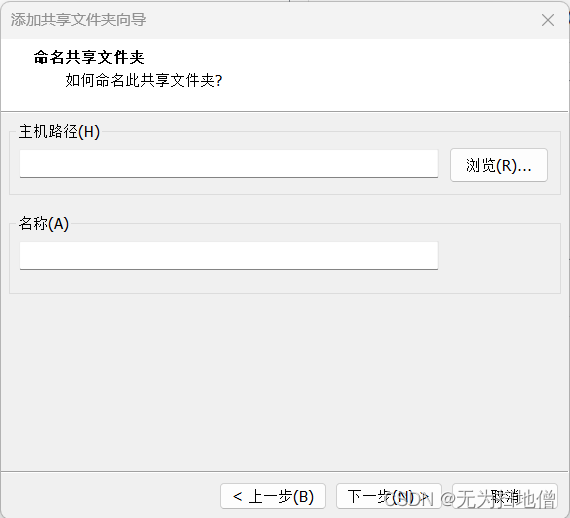
ubuntu与win之间共享文件夹
ubuntu上设置共享文件夹 第一步:点击【设置】或【虚拟机弹窗下面的【设置】选项】 第二步:进入【虚拟机设置】页面,点击【选项】如下图所示 第三步:启用共享文件:点击【总是启用】第四步:添加共享文件&…...

flink处理函数--副输出功能
背景 在flink中,如果你想要访问记录的处理时间或者事件时间,注册定时器,或者是将记录输出到多个输出流中,你都需要处理函数的帮助,本文就来通过一个例子来讲解下副输出 副输出 本文还是基于streaming-with-flink这本…...
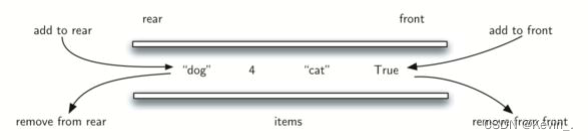
Java数据结构————队列
一 、队列 在Java中,Queue是个接口,底层是通过链表实现的。 只允许在一端进行插入数据操作, 在另一端进行删除数据操作的特殊线性表, 队列具有先进先出FIFO(First In First Out) 。 入队列: 进行插入操作的一端称为…...
办公网络构建
办公网络项目背景 XX州市益智软件科技有限公司是XX市第九职业技术学校校办企业,依托学校人力技术、场地资源,面向市场独立经营、服务社会,主要从事网络设备销售、网络综合布线与网络管理。该公司现租用实训基地二层作为公司的办公经营场地…...
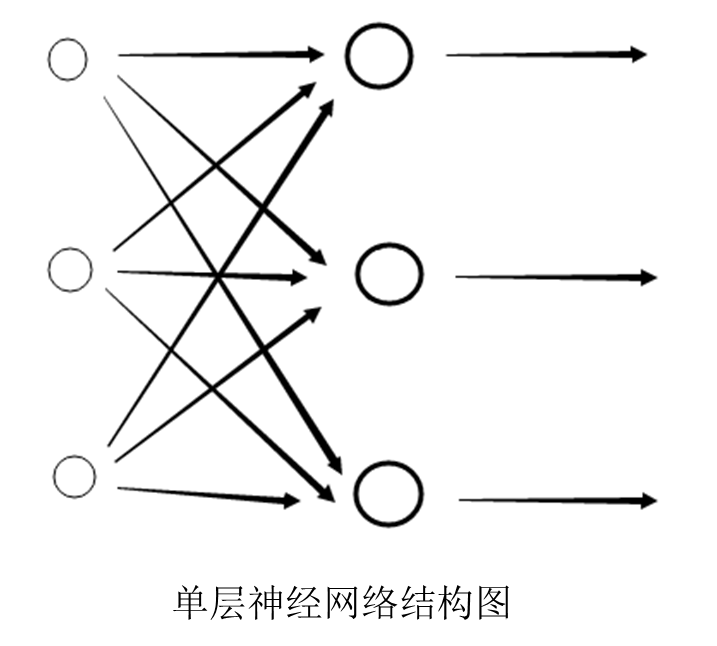
单层神经网络
神经网络 人工神经网络(Artificial Neural Network,ANN),简称神经网络(Neural Network,NN),是一种模仿生物神经网络的结构和功能的数学模型或计算模型。1943年,McCulloc…...
htb-cozyhosting
HTB-CozyHosting https://app.hackthebox.com/machines/CozyHosting ──(kwkl㉿kwkl)-[~] └─$ tail -l /etc/hosts …...
网络安全渗透测试工具之skipfish
网络安全渗透测试工具skipfish介绍 在数字化的时代,Web 应用程序安全成为了首要任务。想象一下,您是一位勇敢的安全冒险家,迎接着那些隐藏在 Web 应用程序中的未知风险。而在这个冒险之旅中,您需要一款强大的工具来帮助您发现漏洞,揭示弱点。而这个工具就是 Skipfish。 …...

【Rust】文件系统
目录 一、读取文件的字符串行 二、避免读取写入同一文件 三、使用内存映射随机访问文件 四、过去 24 小时内修改过的文件名 五、查找给定路径的循环 六、递归查找重名文件 七、使用给定断言递归查找所有文件 八、跳过隐藏文件遍历目录 九、在给定深度的目录࿰…...
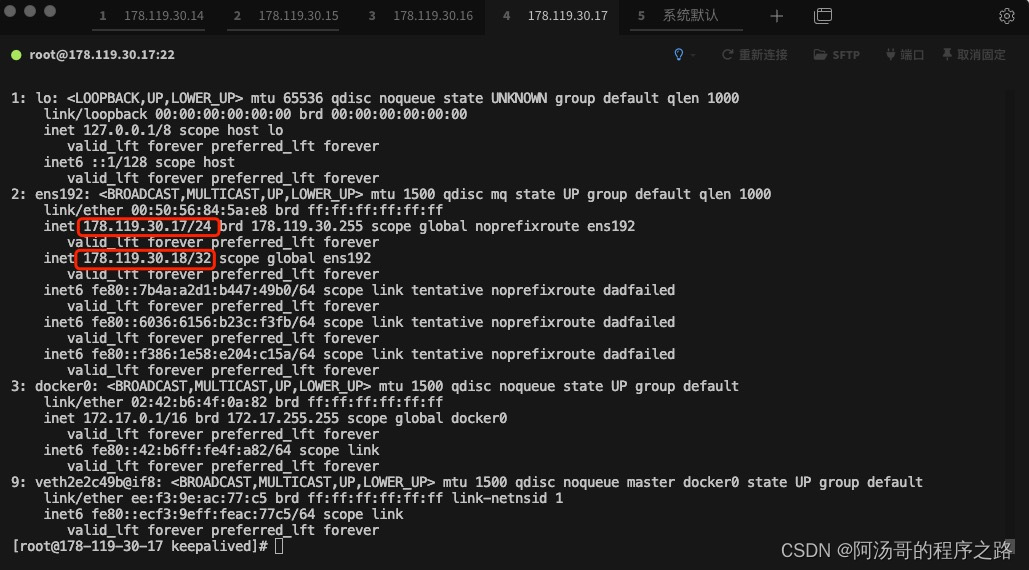
mysql双主双从读写分离
架构图: 详细内容参考: 结果展示: 178.119.30.16(从)- master 178.119.30.17(从)- slave 由上述结果可以看出,产生了主备节点同时抢占VIP的问题(即脑裂问题)…...

postgresql-物化视图
postgresql-物化视图 物化视图创建物化视图刷新物化视图修改物化视图删除物化视图 物化视图 创建物化视图 postgresql使用create materialized view 语句创建视图 create materialized view if not exists name as query [with [NO] data];-- 创建一个包含员工统计信息的物化…...

多层神经网络和激活函数
多层神经网络的结构 多层神经网络就是由单层神经网络进行叠加之后得到的,所以就形成了层的概念,常见的多层神经网络有如下结构: 1)输入层(Input layer),众多神经元(Neuronÿ…...

Visual Studio Code键盘快捷键大全
Visual Studio Code键盘快捷键大全 前言导航快捷键编辑快捷键多光标快捷键终端快捷键调试快捷键文件管理快捷键Git快捷键代码格式化快捷键代码折叠快捷键工作区快捷键Markdown快捷键Zen模式快捷键窗口管理快捷键重构快捷键IntelliSense快捷键测试快捷键扩展快捷键 前言 欢迎来…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个生活电费的缴纳和查询小程序
一、项目初始化与配置 1. 创建项目 ohpm init harmony/utility-payment-app 2. 配置权限 // module.json5 {"requestPermissions": [{"name": "ohos.permission.INTERNET"},{"name": "ohos.permission.GET_NETWORK_INFO"…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...

破解路内监管盲区:免布线低位视频桩重塑停车管理新标准
城市路内停车管理常因行道树遮挡、高位设备盲区等问题,导致车牌识别率低、逃费率高,传统模式在复杂路段束手无策。免布线低位视频桩凭借超低视角部署与智能算法,正成为破局关键。该设备安装于车位侧方0.5-0.7米高度,直接规避树枝遮…...

Python网页自动化Selenium中文文档
1. 安装 1.1. 安装 Selenium Python bindings 提供了一个简单的API,让你使用Selenium WebDriver来编写功能/校验测试。 通过Selenium Python的API,你可以非常直观的使用Selenium WebDriver的所有功能。 Selenium Python bindings 使用非常简洁方便的A…...

【Linux】Linux安装并配置RabbitMQ
目录 1. 安装 Erlang 2. 安装 RabbitMQ 2.1.添加 RabbitMQ 仓库 2.2.安装 RabbitMQ 3.配置 3.1.启动和管理服务 4. 访问管理界面 5.安装问题 6.修改密码 7.修改端口 7.1.找到文件 7.2.修改文件 1. 安装 Erlang 由于 RabbitMQ 是用 Erlang 编写的,需要先安…...

数据结构第5章:树和二叉树完全指南(自整理详细图文笔记)
名人说:莫道桑榆晚,为霞尚满天。——刘禹锡(刘梦得,诗豪) 原创笔记:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 上一篇:《数据结构第4章 数组和广义表》…...
