想要精通算法和SQL的成长之路 - 并查集的运用和案例(省份数量)
想要精通算法和SQL的成长之路 - 并查集的运用
- 前言
- 一. 并查集的使用和模板
- 1.1 初始化
- 1.2 find 查找函数
- 1.3 union 合并集合
- 1.4 connected 判断相连性
- 1.5 完整代码
- 二. 运用案例 - 省份数量
前言
想要精通算法和SQL的成长之路 - 系列导航
一. 并查集的使用和模板
先说一下并查集的相关知识点:
- 含义:并查集,用于维护一组不相交的集合,支持合并两个集合和查询某个元素所属的集合。
- 用途:解决图论、连通性问题和动态连通性等问题。
通俗一点,可以使用并查集的算法题目有哪些特征?
- 需要将
n个不同的元素划分为不相交的集合。 - 开始的时候,每个元素自行成为一个集合,然后需要根据一定的顺序进行 合并。
- 同时还需要 查询 某个元素是否属于哪个集合。
因此并查集的基本操作可以包含两个:
- 合并:将两个不相交的集合合并成一个集合。(将其中一个集合的根节点连接到另一个集合的根节点上)
- 查找:根据某个元素,寻找到它所在集合的根节点。
1.1 初始化
首先我们考虑下,并查集里面需要有哪些数据结构:
- 需要一个
parent[]数组,用来存储每个元素对应的根节点。 - 再来一个
rank[]数组,代表以每个元素作为根节点,其所在集合的大小。即代表某个集合的深度。 - 再来一个
sum字段,代表当前的集合个数。
public class UnionFind {/*** 表示节点i的父节点*/private int[] parent;/*** 表示以节点i为根节点的子树的深度,初始时每个节点的深度都为0*/private int[] rank;private int sum;public UnionFind(int n) {parent = new int[n];rank = new int[n];// 初始时每个节点的父节点都是它自己for (int i = 0; i < n; i++) {parent[i] = i;}sum = n;}
}
1.2 find 查找函数
特征:
- 入参:元素
x。 - 要做的事情:不断地向上递归寻找这个
x的根节点。 - 递归终止条件:找到根节点。(根节点和元素本身一致)
代码如下:
public int find(int x) {while (x != parent[x]) {x = parent[x];}return x;
}
1.3 union 合并集合
特征:
- 入参:元素
x和y。 - 要做的事情:分别找到这两个元素的根节点:
rootX和rootY。 - 如果俩元素的根节点是同一个,说明他们在一个集合当中,不需要任何操作。
- 倘若两个元素的根节点不一样,根据两个集合的深度来判断。将深度小的那个集合,合并到深度大的集合中。同时更新对应的根节点和深度大小。
除此之外,我们还可以写一个简单的函数,用来判断两个元素是否处于同一个集合当中(或者是是否相连)
public void union(int x, int y) {int rootX = find(x);int rootY = find(y);// 如果两个元素的根节点一致,不需要合并if (rootX == rootY) {return;}// 如果根节点 rootX 的深度 > rootY。if (rank[rootX] > rank[rootY]) {// 那么将以rootY作为根节点的集合加入到rootX对应的集合当中rank[rootX] += rank[rootY];// 同时改变rootY的根节点,指向rootX。parent[rootY] = rootX;} else {// 反之rank[rootY] += rank[rootX];parent[rootX] = rootY;}
}
1.4 connected 判断相连性
/*** 判断两个节点是否在同一个集合中
*/
public boolean connected(int x, int y) {return find(x) == find(y);
}
1.5 完整代码
/*** @author Zong0915* @date 2023/10/4 下午2:52*/
public class UnionFind {/*** 表示节点i的父节点*/private int[] parent;/*** 表示以节点i为根节点的子树的深度,初始时每个节点的深度都为0*/private int[] rank;private int sum;public UnionFind(int n) {parent = new int[n];rank = new int[n];// 初始时每个节点的父节点都是它自己for (int i = 0; i < n; i++) {parent[i] = i;}sum = n;}public int find(int x) {while (x != parent[x]) {x = parent[x];}return x;}public void union(int x, int y) {int rootX = find(x);int rootY = find(y);// 如果两个元素的根节点一致,不需要合并if (rootX == rootY) {return;}// 如果根节点 rootX 的深度 > rootY。if (rank[rootX] > rank[rootY]) {// 那么将以rootY作为根节点的集合加入到rootX对应的集合当中rank[rootX] += rank[rootY];// 同时改变rootY的根节点,指向rootX。parent[rootY] = rootX;} else {// 反之rank[rootY] += rank[rootX];parent[rootX] = rootY;}}/*** 判断两个节点是否在同一个集合中*/public boolean connected(int x, int y) {return find(x) == find(y);}
}
二. 运用案例 - 省份数量
原题链接
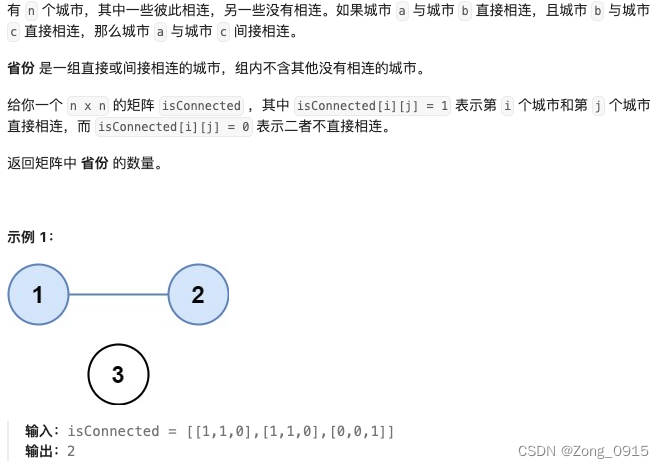
我们在并查集模板的基础上进行改造:
class UnionFind {private int[] rank;// 每个省份具有的城市数量private int[] parent;// 每个城市对应的根节点(省份)private int sum;// 省份的数量public UnionFind(int[][] isConnected) {int len = isConnected.length;// 初始化,省份数量和提供的城市数量一致sum = len;// 每个集合具有的城市数量为1rank = new int[len];parent = new int[len];Arrays.fill(rank, 1);// 根节点指向自己for (int i = 0; i < len; i++) {parent[i] = i;}}public int find(int x) {while (x != parent[x]) {x = parent[x];}return x;}public void union(int x, int y) {int rootX = find(x);int rootY = find(y);// 如果两个元素的根节点一致,不需要合并if (rootX == rootY) {return;}// 如果根节点 rootX 的深度 > rootY。if (rank[rootX] > rank[rootY]) {// 那么将以rootY作为根节点的集合加入到rootX对应的集合当中rank[rootX] += rank[rootY];// 同时改变rootY的根节点,指向rootX。parent[rootY] = rootX;} else {// 反之rank[rootY] += rank[rootX];parent[rootX] = rootY;}// 合并成功,那么总集合数量要减1sum--;}
}
不过本题目当中,对于rank这个属性没有什么作用,最终看的是sum属性。因此大家可以把这个属性相关的给去除。
最后来看代码部分:
public int findCircleNum(int[][] isConnected) {// 初始化构造UnionFind unionFind = new UnionFind(isConnected);int len1 = isConnected.length;int len2 = isConnected[0].length;for (int i = 0; i < len1; i++) {for (int j = 0; j < len2; j++) {// 如果是相连的,那么将城市 i 和 j 合并if (isConnected[i][j] == 1) {unionFind.union(i, j);}}}// 最后返回集合个数(即省份的个数)return unionFind.sum;
}
最终代码如下:
public class Test547 {public int findCircleNum(int[][] isConnected) {UnionFind unionFind = new UnionFind(isConnected);int len1 = isConnected.length;int len2 = isConnected[0].length;for (int i = 0; i < len1; i++) {for (int j = 0; j < len2; j++) {// 如果是相连的,那么将城市 i 和 j 合并if (isConnected[i][j] == 1) {unionFind.union(i, j);}}}return unionFind.sum;}class UnionFind {private int[] rank;// 每个省份具有的城市数量private int[] parent;// 每个城市对应的根节点(省份)private int sum;// 省份的数量public UnionFind(int[][] isConnected) {int len = isConnected.length;// 初始化,省份数量和提供的城市数量一致sum = len;// 每个集合具有的城市数量为1rank = new int[len];parent = new int[len];Arrays.fill(rank, 1);// 根节点指向自己for (int i = 0; i < len; i++) {parent[i] = i;}}public int find(int x) {while (x != parent[x]) {x = parent[x];}return x;}public void union(int x, int y) {int rootX = find(x);int rootY = find(y);// 如果两个元素的根节点一致,不需要合并if (rootX == rootY) {return;}// 如果根节点 rootX 的深度 > rootY。if (rank[rootX] > rank[rootY]) {// 那么将以rootY作为根节点的集合加入到rootX对应的集合当中rank[rootX] += rank[rootY];// 同时改变rootY的根节点,指向rootX。parent[rootY] = rootX;} else {// 反之rank[rootY] += rank[rootX];parent[rootX] = rootY;}sum--;}}
}
相关文章:

想要精通算法和SQL的成长之路 - 并查集的运用和案例(省份数量)
想要精通算法和SQL的成长之路 - 并查集的运用 前言一. 并查集的使用和模板1.1 初始化1.2 find 查找函数1.3 union 合并集合1.4 connected 判断相连性1.5 完整代码 二. 运用案例 - 省份数量 前言 想要精通算法和SQL的成长之路 - 系列导航 一. 并查集的使用和模板 先说一下并查集…...

解决内网拉取企微会话存档代理问题的一种办法
问题:客户的服务都是内网的,不能直接访问外网;访问外网的话需要走kong网关才能出去。 会话存档官网说可以使用socket5、http方式拉取会话存档;我这边尝试了直接使用kong网关的ip和端口配置进去,是访问不了的 我后面就…...

二十二,加上各种贴图
使用pbr的各种贴图,albedo,金属度,ao,法线,粗糙度,可以更好的控制各个片元 1,先加上纹理坐标 texCoords->push_back(osg::Vec2(xSegment, ySegment)); geom->setVertexAttribArray(3, texCoords, osg::Array::BI…...

新版校园跑腿独立版小程序源码 多校版本,多模块,适合跑腿,外卖,表白,二手,快递等校园服务
最新校园跑腿小程序源码 多校版本,多模块,适合跑腿,外卖,表白,二手,快递等校园服务 此版本为独立版本,不需要** 直接放入就可以 需要自己准备好后台的服务器,已认证的小程序…...
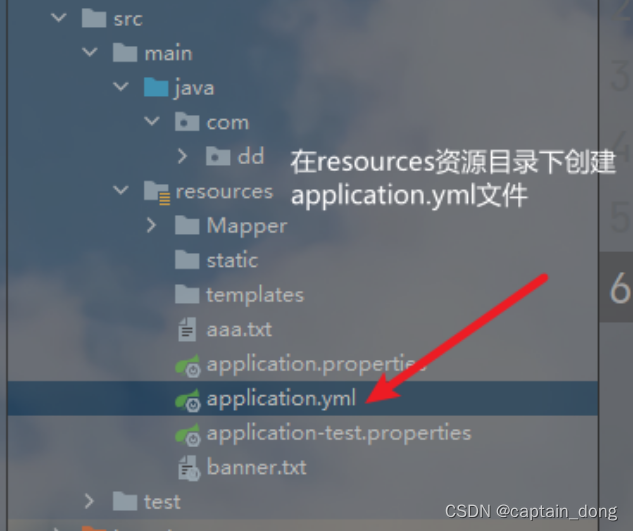
SpringBoot banner 样式 自动生成
目录 SpringBoot banner 样式 自动生成 图案网站: 1.第一步创建banner.txt文件 2.访问网站Ascii艺术字实现个性化Spring Boot启动banner图案,轻松修改更换banner.txt文件内容,收集了丰富的banner艺术字和图,并且支持中文banner下…...
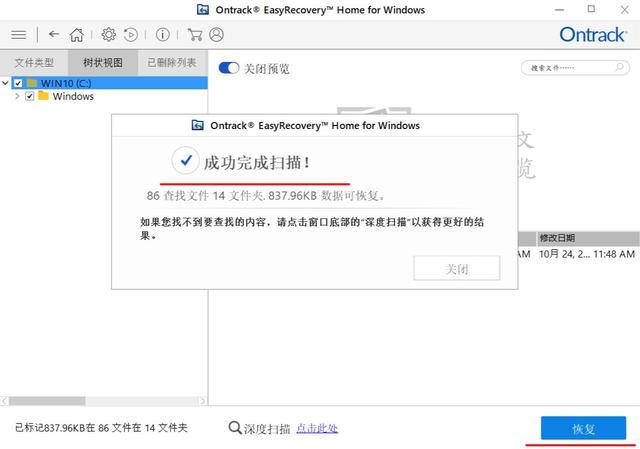
回收站里面删除的照片如何恢复?
现在拍照已经成为人们生活中的一种方式,照片为我们保留了许多珍贵而美好的回忆。大家通常会把重要的照片保存在硬盘里,但当不小心把照片移入回收站并彻底删除时,情况就有点糟糕了。那么,回收站里删除的照片还有办法恢复吗…...

Qt model/view 理解 2
这是我对 Qt 的 model/view 内容理解的第二篇 blog,在第一篇文章中,介绍 QTableView 和 QAbstractTableModel,实现显示了对数据源的显示,但是显示的格式和修改的模式都是按照 View 控件的自显示方式。在此,使用 Qt 自带…...
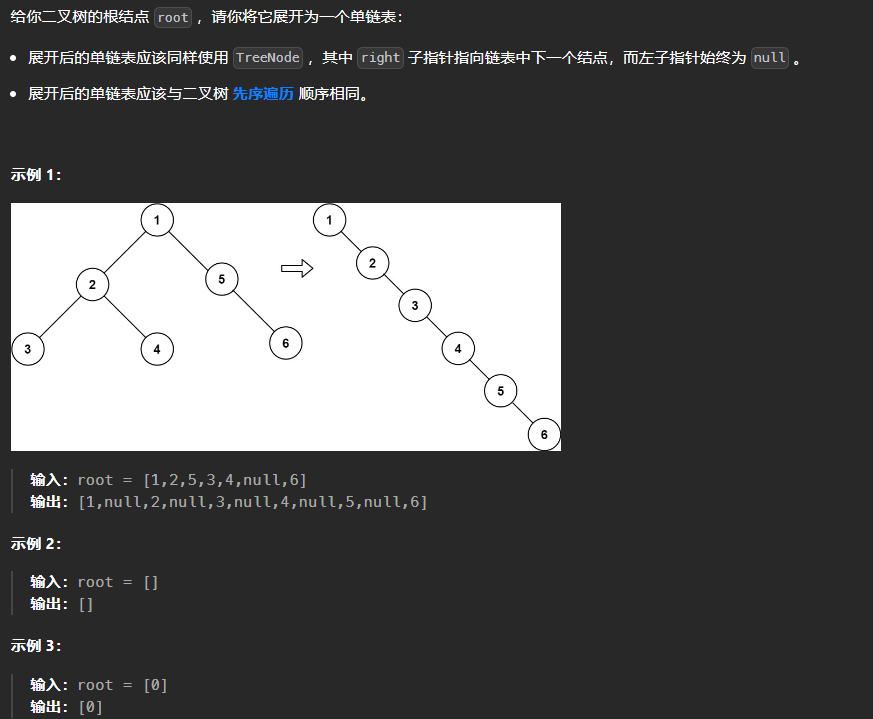
【LeetCode热题100】--114.二叉树展开为链表
114.二叉树展开为链表 方法一:对二叉树进行先序遍历,得到各个节点被访问到的顺序,利用数组存储下来,然后在先序遍历之后更新每个节点的左右节点的信息,将二叉树展开为链表 /*** Definition for a binary tree node.* …...

Java | Maven(知识点查询)
文章目录 Maven知识速查1. Maven概述2. Maven的作用3. Maven的下载4. Maven的环境配置5. Maven 的基础组成5.1 Maven仓库5.1.1 本地仓库配置:5.1.2 中央仓库配置:5.1.3 镜像仓库配置 5.2 Maven坐标 6. Maven项目6.1 手工创建Maven项目6.2 自动构建项目 7…...
Vmware 静态网络配置
概述 仅主机模式(VMware1):使用host-only的方式是不能和外界通信的,只能够和本机的物理网卡通信 桥接(VMnet0):使用桥接的方式使得自己的虚拟机和自己的真实机网卡在同一个网段 NAT࿰…...

【数据结构--八大排序】之希尔排序
💐 🌸 🌷 🍀 🌹 🌻 🌺 🍁 🍃 🍂 🌿 🍄🍝 🍛 🍤 📃个人主页 :阿然成长日记 …...

Linux中生成so库的文件引用另一个so库问题的解决
文章目录 一、问题介绍二、问题解决 一、问题介绍 由于项目需求,需要将一个“编译时引用了另一个动态链接库”的文件(名为main.c),再编译成一个动态链接库。 简要说明一下,即原本的项目代码里,包含main.c…...

EDI是连接原始电子商务和现代电子商务的纽带
EDI是连接原始电子商务和现代电子商务的纽带。 EDI(Electronic Data Interchange,电子数据交换)是一种电子通信技术,用于在不同组织之间以结构化和标准化的方式交换业务文档和数据。EDI使企业能够更有效地与供应商、客户和合作伙…...
星宿UI2.4资源付费变现小程序源码 支持流量主
第一个小程序为星宿小程序 目前是最新版2.0 搭建星宿需要:备用域名 服务器 微信小程序账号 功能:文章展示 文章分类 资源链接下载 轮播图 直接下载附件功能 很多 很适合做资源类分享 源码下载:https://download.csdn.net/download/m0_6604…...

代码随想录训练营二刷第四十六天 | 完全背包 518. 零钱兑换 II 377. 组合总和 Ⅳ
代码随想录训练营二刷第四十六天 | 518. 零钱兑换 II 377. 组合总和 Ⅳ 一、518. 零钱兑换 II 题目链接:https://leetcode.cn/problems/coin-change-ii/ 思路:完全背包求组合数,递推公式dp[j]dp[j-nums[i]]。 求组合数,物品在外…...
python安装第三方模块方法
正常情况下安装python第三方模块没啥说的,但是由于python安装模块默认是在外网下载安装,牵扯外网网速问题,所以可以配置下使用国内某镜像源来下载模块 python -m pip install xxxxxxxxxxx 和 pip install xxxxxxxxxx 的命令都可下载安装第三…...

广西小贷公司设立及小贷牌照申请政策要求
关于广西小额贷款公司设立及小贷牌照申请,依据《关于小额贷款公司试点的指导意见》(银监发〔2008〕23号);《广西壮族自治区小额贷款公司管理办法》(桂政发〔2009〕71号);《广西壮族自治区人民政…...

PyTorch应用实战二:实现卷积神经网络进行图像分类
文章目录 实验环境MNIST数据集1.网络结构2.程序实现2.1 导入相关库2.2 构建卷积神经网络模型2.3 加载MNIST数据集2.4 训练模型 附:系列文章 实验环境 python3.6 pytorch1.8.0 import torch print(torch.__version__)1.8.0MNIST数据集 MNIST数字数据集是一组手写…...
)
面试系列 - Java常见算法(二)
目录 一、排序算法 1、插入排序(Insertion Sort) 2、归并排序(Merge Sort) 二、图形算法 1、最短路径算法(Dijkstra算法、Floyd-Warshall算法) Dijkstra算法 Floyd-Warshall算法 2、最小生成树算法&…...
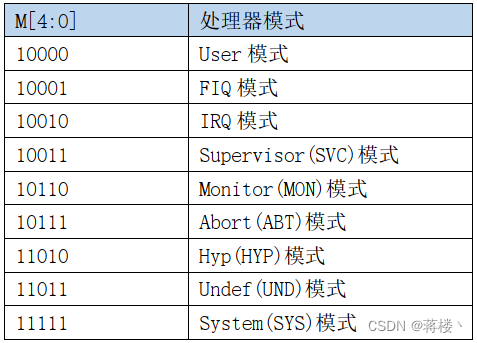
Cortex-A9 架构
一、Cortex-A 处理器运行模式 Cortex-A9处理器有 9中处理模式,如下表所示: 九种运行模式 在上表中,除了User(USR)用户模式以外,其它8种运行模式都是特权模式,在特权模式下,程序可以访问所有的系统资源。这…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数
高效线程安全的单例模式:Python 中的懒加载与自定义初始化参数 在软件开发中,单例模式(Singleton Pattern)是一种常见的设计模式,确保一个类仅有一个实例,并提供一个全局访问点。在多线程环境下,实现单例模式时需要注意线程安全问题,以防止多个线程同时创建实例,导致…...
