面试系列 - Java常见算法(二)
目录
一、排序算法
1、插入排序(Insertion Sort)
2、归并排序(Merge Sort)
二、图形算法
1、最短路径算法(Dijkstra算法、Floyd-Warshall算法)
Dijkstra算法
Floyd-Warshall算法
2、最小生成树算法(Prim算法、Kruskal算法)
Prim算法
Kruskal算法
一、排序算法
1、插入排序(Insertion Sort)
插入排序(Insertion Sort)是一种简单的排序算法,它的工作原理是逐步构建有序序列。该算法每次将一个未排序的元素插入到已排序序列的适当位置,直到所有元素都被排序为止。插入排序通常是稳定的,适用于小型数据集或基本有序的数据集。
工作原理:
- 将第一个元素视为已排序序列。
- 从第二个元素开始,将其插入已排序序列的适当位置,以确保已排序序列仍然有序。
- 重复步骤2,直到所有元素都被插入到适当的位置,形成完全有序的序列。
public class InsertionSort {public static void insertionSort(int[] arr) {int n = arr.length;for (int i = 1; i < n; i++) {int currentElement = arr[i];int j = i - 1;// 从已排序部分的末尾开始,依次比较并移动元素while (j >= 0 && arr[j] > currentElement) {arr[j + 1] = arr[j]; // 向右移动元素j--;}// 插入当前元素到合适的位置arr[j + 1] = currentElement;}}public static void main(String[] args) {int[] arr = {12, 11, 13, 5, 6};insertionSort(arr);System.out.println("排序后的数组:");for (int num : arr) {System.out.print(num + " ");}}
}
在这个Java示例中,insertionSort方法实现了插入排序算法。它遍历数组,将每个元素插入已排序部分的适当位置,以保持已排序部分的有序性。
请注意,插入排序是一个稳定的排序算法,适用于小型数据集或基本有序的数据集。然而,对于大型数据集,其时间复杂度为O(n^2),性能相对较低,可以考虑更高效的排序算法如快速排序或归并排序。
2、归并排序(Merge Sort)
归并排序(Merge Sort)是一种分治算法,它将一个大问题分解为多个小问题,然后将这些小问题的解合并在一起以获得最终的解决方案。归并排序的主要思想是将数组分成两半,递归地对每一半进行排序,然后将两个已排序的子数组合并成一个有序的数组。它是一种稳定的排序算法,时间复杂度为O(nlogn),适用于各种数据集大小。
public class MergeSort {public static void mergeSort(int[] arr) {if (arr == null || arr.length <= 1) {return; // 如果数组为空或只有一个元素,无需排序}// 计算中间索引int middle = arr.length / 2;// 创建左右子数组int[] left = new int[middle];int[] right = new int[arr.length - middle];// 将元素分配到左右子数组System.arraycopy(arr, 0, left, 0, middle);System.arraycopy(arr, middle, right, 0, arr.length - middle);// 递归地对左右子数组进行排序mergeSort(left);mergeSort(right);// 合并两个已排序的子数组merge(arr, left, right);}public static void merge(int[] result, int[] left, int[] right) {int i = 0, j = 0, k = 0;// 比较并合并左右子数组的元素while (i < left.length && j < right.length) {if (left[i] <= right[j]) {result[k++] = left[i++];} else {result[k++] = right[j++];}}// 处理左子数组中剩余的元素while (i < left.length) {result[k++] = left[i++];}// 处理右子数组中剩余的元素while (j < right.length) {result[k++] = right[j++];}}public static void main(String[] args) {int[] arr = {12, 11, 13, 5, 6, 7};mergeSort(arr);System.out.println("排序后的数组:");for (int num : arr) {System.out.print(num + " ");}}
}
在上面的Java示例中,mergeSort方法实现了归并排序算法,它递归地将数组分为左右两半,然后合并这两个已排序的子数组。merge方法用于合并两个子数组并将其排序为一个有序数组。
归并排序是一种高效且稳定的排序算法,适用于各种不同大小的数据集。由于其时间复杂度为O(nlogn),它在处理大型数据集时表现出色。
二、图形算法
1、最短路径算法(Dijkstra算法、Floyd-Warshall算法)
最短路径算法用于在图中查找两个节点之间的最短路径或最短距离。在网络路由、导航系统、交通规划等领域广泛应用。以下是Dijkstra算法和Floyd-Warshall算法的详细说明:
Dijkstra算法
Dijkstra算法用于计算一个源节点到图中所有其他节点的最短路径。它的基本思想是通过逐步扩展最短路径集合来找到最短路径。
算法步骤:
-
初始化一个距离数组
dist[],用于存储从源节点到其他节点的距离估计值。将源节点的距离初始化为0,其他节点初始化为无穷大。 -
创建一个空的集合
visited[],用于跟踪已访问的节点。 -
重复以下步骤,直到
visited[]包含所有节点: a. 从未访问的节点中选择距离最短的节点u。 b. 标记节点u为已访问。 c. 更新与节点u相邻的节点v的距离估计值,如果通过u到v的路径距离更短。 -
当所有节点都被访问后,
dist[]中存储了从源节点到每个节点的最短距离。
import java.util.*;public class DijkstraAlgorithm {public static int[] dijkstra(int[][] graph, int source) {int n = graph.length;int[] dist = new int[n];boolean[] visited = new boolean[n];Arrays.fill(dist, Integer.MAX_VALUE);dist[source] = 0;for (int count = 0; count < n - 1; count++) {int u = minDistance(dist, visited);visited[u] = true;for (int v = 0; v < n; v++) {if (!visited[v] && graph[u][v] != 0 && dist[u] != Integer.MAX_VALUE && dist[u] + graph[u][v] < dist[v]) {dist[v] = dist[u] + graph[u][v];}}}return dist;}private static int minDistance(int[] dist, boolean[] visited) {int min = Integer.MAX_VALUE;int minIndex = -1;for (int i = 0; i < dist.length; i++) {if (!visited[i] && dist[i] <= min) {min = dist[i];minIndex = i;}}return minIndex;}public static void main(String[] args) {int[][] graph = {{0, 4, 0, 0, 0, 0, 0, 8, 0},{4, 0, 8, 0, 0, 0, 0, 11, 0},{0, 8, 0, 7, 0, 4, 0, 0, 2},{0, 0, 7, 0, 9, 14, 0, 0, 0},{0, 0, 0, 9, 0, 10, 0, 0, 0},{0, 0, 4, 14, 10, 0, 2, 0, 0},{0, 0, 0, 0, 0, 2, 0, 1, 6},{8, 11, 0, 0, 0, 0, 1, 0, 7},{0, 0, 2, 0, 0, 0, 6, 7, 0}};int source = 0;int[] dist = dijkstra(graph, source);for (int i = 0; i < dist.length; i++) {System.out.println("Distance from " + source + " to " + i + ": " + dist[i]);}}
}
Floyd-Warshall算法
Floyd-Warshall算法用于计算图中所有节点之间的最短路径。它通过动态规划的方式计算所有节点对之间的最短路径。
算法步骤:
-
创建一个二维数组
dist[][],其中dist[i][j]表示从节点i到节点j的最短路径距离,初始化为无穷大。 -
初始化
dist[i][i]为0,表示节点到自身的距离为0。 -
对于每一条边
(u, v),将dist[u][v]初始化为边的权重。 -
遍历所有节点对
(i, j),对于每对节点,尝试通过节点k(k为0到n-1)来缩短路径dist[i][j],即dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j])。 -
当遍历完所有节点对时,
dist[][]中存储了所有节点之间的最短路径。
public class FloydWarshallAlgorithm {public static void floydWarshall(int[][] graph) {int n = graph.length;int[][] dist = new int[n][n];for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {dist[i][j] = graph[i][j];}}for (int k = 0; k < n; k++) {for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {if (dist[i][k] != Integer.MAX_VALUE && dist[k][j] != Integer.MAX_VALUE&& dist[i][k] + dist[k][j] < dist[i][j]) {dist[i][j] = dist[i][k] + dist[k][j];}}}}for (int i = 0; i < n; i++) {for (int j = 0; j < n; j++) {System.out.println("Shortest distance from " + i + " to " + j + ": " + dist[i][j]);}}}public static void main(String[] args) {int[][] graph = {{0, 5, Integer.MAX_VALUE, 10},{Integer.MAX_VALUE, 0, 3, Integer.MAX_VALUE},{Integer.MAX_VALUE, Integer.MAX_VALUE, 0, 1},{Integer.MAX_VALUE, Integer.MAX_VALUE, Integer.MAX_VALUE, 0}};floydWarshall(graph);}
}
Dijkstra算法适用于单源最短路径问题,而Floyd-Warshall算法适用于所有节点对之间的最短路径问题。选择算法取决于问题的规模和要求。
2、最小生成树算法(Prim算法、Kruskal算法)
最小生成树算法(Minimum Spanning Tree Algorithms)用于在一个连通的加权图中找到一个包含所有节点的子图,并且这个子图是树(没有回路),同时具有最小的总权重。两个常用的最小生成树算法是Prim算法和Kruskal算法。
Prim算法
Prim算法从一个初始节点开始,逐步构建最小生成树,每次选择与当前树连接最近的节点,并将其添加到最小生成树中。这个过程持续进行,直到所有节点都包含在生成树中。
算法步骤:
- 选择一个起始节点。
- 初始化一个空的生成树和一个优先队列(或最小堆)来存储边的权重。
- 将起始节点加入生成树。
- 将所有与起始节点相邻的边加入优先队列。
- 从队列中取出具有最小权重的边(边的一端在生成树中,另一端不在),将其另一端的节点加入生成树,并将与新节点相邻的边加入队列。
- 重复步骤5,直到生成树包含了所有节点。
import java.util.*;public class PrimAlgorithm {public static void primMST(int[][] graph) {int n = graph.length;int[] parent = new int[n]; // 用于存储生成树的父节点int[] key = new int[n]; // 用于存储节点到生成树的最小权重boolean[] inMST = new boolean[n]; // 记录节点是否已在生成树中Arrays.fill(key, Integer.MAX_VALUE);key[0] = 0; // 从第一个节点开始for (int i = 0; i < n - 1; i++) {int u = minKey(key, inMST);inMST[u] = true;for (int v = 0; v < n; v++) {if (graph[u][v] != 0 && !inMST[v] && graph[u][v] < key[v]) {parent[v] = u;key[v] = graph[u][v];}}}printMST(parent, graph);}private static int minKey(int[] key, boolean[] inMST) {int min = Integer.MAX_VALUE;int minIndex = -1;for (int i = 0; i < key.length; i++) {if (!inMST[i] && key[i] < min) {min = key[i];minIndex = i;}}return minIndex;}private static void printMST(int[] parent, int[][] graph) {System.out.println("Edge \tWeight");for (int i = 1; i < parent.length; i++) {System.out.println(parent[i] + " - " + i + "\t" + graph[i][parent[i]]);}}public static void main(String[] args) {int[][] graph = {{0, 2, 0, 6, 0},{2, 0, 3, 8, 5},{0, 3, 0, 0, 7},{6, 8, 0, 0, 9},{0, 5, 7, 9, 0}};primMST(graph);}
}
Kruskal算法
Kruskal算法首先将所有边按权重排序,然后按照权重递增的顺序逐个加入生成树,但要确保加入的边不会形成回路。它使用并查集数据结构来检测回路。
算法步骤:
- 将图中的所有边按权重升序排序。
- 初始化一个空的生成树。
- 从排序后的边中选择一条最小权重的边。
- 检查加入这条边后是否会形成回路。如果不会,将边加入生成树。
- 重复步骤3和4,直到生成树包含了所有节点或没有更多的边可供选择。
import java.util.*;class Edge implements Comparable<Edge> {int src, dest, weight;public int compareTo(Edge compareEdge) {return this.weight - compareEdge.weight;}
}public class KruskalAlgorithm {public static void kruskalMST(int[][] graph) {int n = graph.length;List<Edge> edges = new ArrayList<>();for (int i = 0; i < n; i++) {for (int j = i + 1; j < n; j++) {if (graph[i][j] != 0) {Edge edge = new Edge();edge.src = i;edge.dest = j;edge.weight = graph[i][j];edges.add(edge);}}}Collections.sort(edges);int[] parent = new int[n];Arrays.fill(parent, -1);List<Edge> mstEdges = new ArrayList<>();int mstWeight = 0;for (Edge edge : edges) {int x = find(parent, edge.src);int y = find(parent, edge.dest);if (x != y) {mstEdges.add(edge);mstWeight += edge.weight;union(parent, x, y);}}printMST(mstEdges);}private static int find(int[] parent, int node) {if (parent[node] == -1) {return node;}return find(parent, parent[node]);}private static void union(int[] parent, int x, int y) {int xRoot = find(parent, x);int yRoot = find(parent, y);parent[xRoot] = yRoot;}private static void printMST(List<Edge> mstEdges) {System.out.println("Edge \tWeight");for (Edge edge : mstEdges) {System.out.println(edge.src + " - " + edge.dest + "\t" + edge.weight);}}public static void main(String[] args) {int[][] graph = {{0, 2, 0, 6, 0},{2, 0, 3, 8, 5},{0, 3, 0, 0, 7},{6, 8, 0, 0, 9},{0, 5, 7, 9, 0}};kruskalMST(graph);}
}
Prim算法和Kruskal算法都可以用于找到最小生成树,选择哪个算法取决于具体的问题和图的规模。
相关文章:
)
面试系列 - Java常见算法(二)
目录 一、排序算法 1、插入排序(Insertion Sort) 2、归并排序(Merge Sort) 二、图形算法 1、最短路径算法(Dijkstra算法、Floyd-Warshall算法) Dijkstra算法 Floyd-Warshall算法 2、最小生成树算法&…...
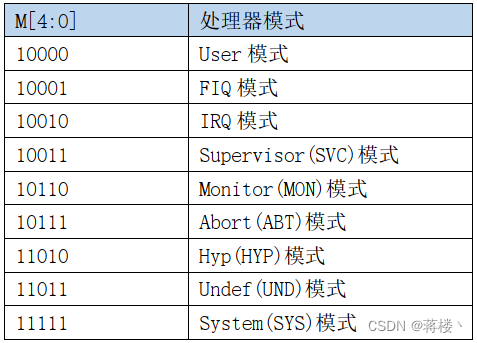
Cortex-A9 架构
一、Cortex-A 处理器运行模式 Cortex-A9处理器有 9中处理模式,如下表所示: 九种运行模式 在上表中,除了User(USR)用户模式以外,其它8种运行模式都是特权模式,在特权模式下,程序可以访问所有的系统资源。这…...
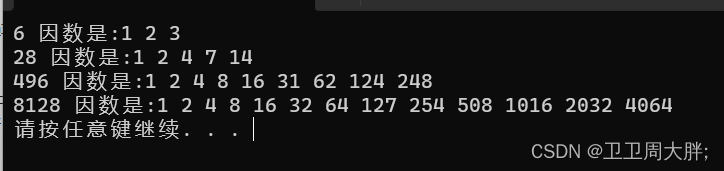
【C语言】循环结构程序设计(第二部分 -- 习题讲解)
前言:昨天我们学习了C语言中循环结构程序设计,并分析了循环结构的特点和实现方法,有了初步编写循环程序的能力,那么今天我们通过一些例子来进一步掌握循环程序的编写和应用。 💖 博主CSDN主页:卫卫卫的个人主页 💞 &am…...
UGUI交互组件Toggle
一.Toggle对象的构造 Toggle和Button类似,是交互组件的一种 如果所示,通过菜单创建了两个Toggle,Toggle2中更换了背景和标记资源 对象说明Toggle含有Toggle组件的对象Background开关背景Checkmark开关选中标记Label名称文本 二.Toggle组件属…...

亲,您的假期余额已经严重不足了......
引言 大家好,我是亿元程序员,一位有着8年游戏行业经验的主程。 转眼八天长假已经接近尾声了,今天来总结一下大家的假期,聊一聊假期关于学习的看法,并预估一下大家节后大家上班时的样子。 1.放假前一天 即将迎来八天…...
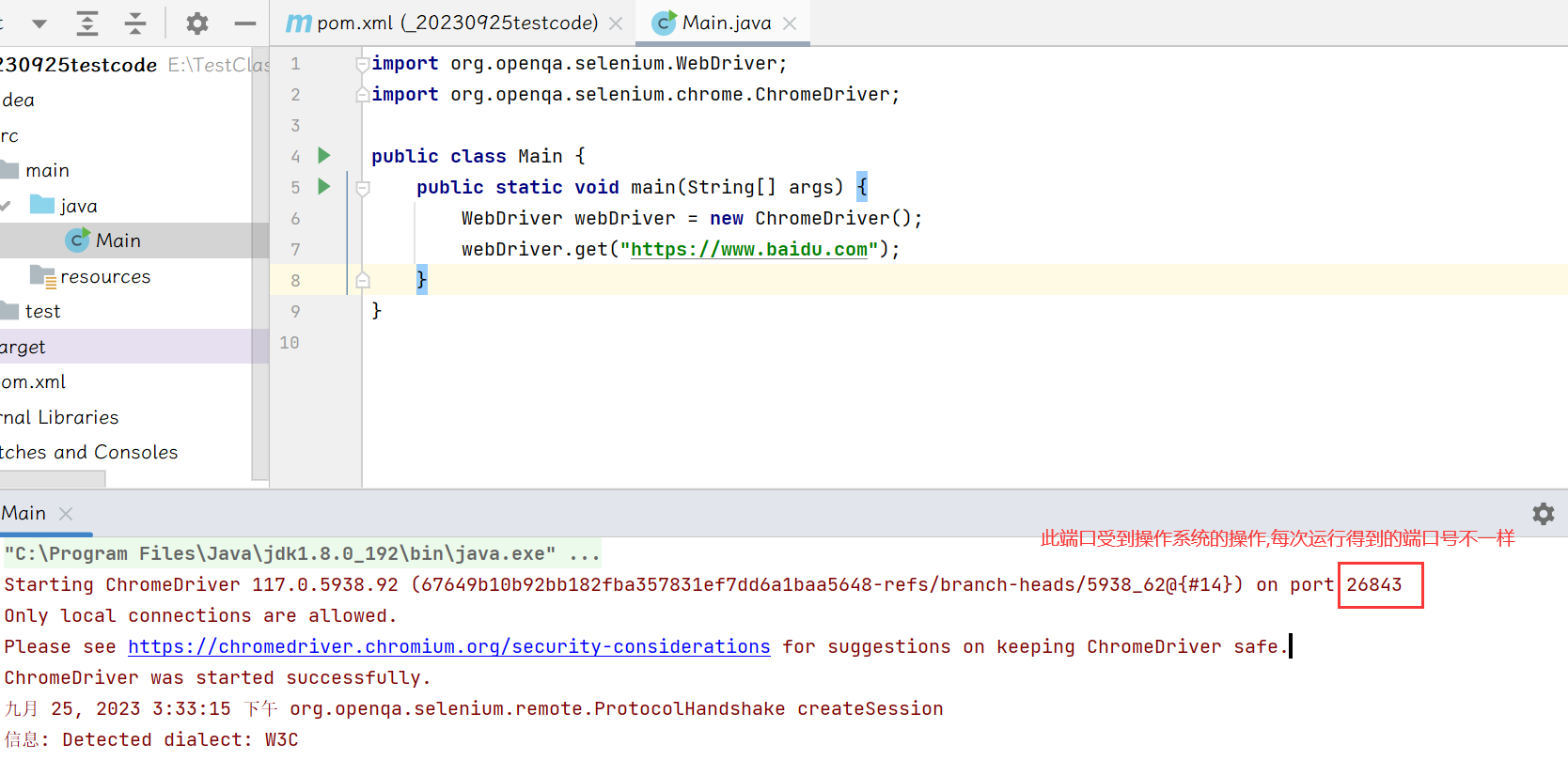
【软件测试】自动化测试selenium(一)
文章目录 一. 什么是自动化测试二. Selenium的介绍1. Selenium是什么2. Selenium的特点3. Selenium的工作原理4. SeleniumJava的环境搭建 一. 什么是自动化测试 自动化测试是指使用软件工具或脚本来执行测试任务的过程,以替代人工进行重复性、繁琐或耗时的测试活动…...
Nginx实现动静分离
一、概述 1、什么是动静分离 动静分离是让动态网站里的动态网页根据一定规则把不变的资源和经常变的资源区分开来,动静资源做好了拆分以后,我们就可以根据静态资源的特点将其做缓存操作,这就是网站静态化处理的核心思路。 动静分离简单的概…...

【算法题】309. 买卖股票的最佳时机含冷冻期
题目: 给定一个整数数组prices,其中第 prices[i] 表示第 i 天的股票价格 。 设计一个算法计算出最大利润。在满足以下约束条件下,你可以尽可能地完成更多的交易(多次买卖一支股票): 卖出股票后,你无法在…...

1951-2011年长序列高时空分辨率月尺度温度和降水数据集
简介 长序列高时空分辨率月尺度温度和降水数据集,基于中国及周边国家共1153个气温站点和1202个降水站点数据,利用ANUSPLIN软件插值,重建了1951−2011年中国月值气温和降水量的高空间分辨率0.025(~2.5km)格点数据集&am…...
十天学完基础数据结构-第六天(树(Tree))
树的基本概念 树是一种层次性的数据结构,它由节点组成,这些节点按照层次关系相互连接。树具有以下基本概念: 根节点:树的顶部节点,没有父节点。 子节点:树中每个节点可以有零个或多个子节点。 叶节点&am…...
RobotFramework流程控制(最新版本)
文章目录 一 分支流程1. 关键字:Run Keyword If2. 关键字:IF/ELSE3. 嵌套IF/ELSE4. 关键字:Set Variable If 二 循环流程1. 普通FOR循环2. 嵌套FOR循环3. 退出循环4. 其它常用循环 一 分支流程 1. 关键字:Run Keyword If Run Key…...

win11 好用的 快捷方式 --chatGPT
gpt: Windows 11引入了许多新的功能和改进,同时也包括一些实用的快捷方式和功能。以下是一些Windows 11中的常用快捷方式: 1. **Win D**:最小化或还原所有打开的窗口,显示桌面。 2. **Win E**:打开文件资源管理器…...

在大数据相关技术中,HBase是个分布的、面向列的开源数据库,是一个适合于非结构化数据存储的数据库。
HDFS,适合运行在通用硬件上的分布式文件系统,是一个高度容错性的系统,适合部署在廉价的机器上。Hbase,是一个分布式的、面向列的开源数据库,适合于非结构化数据存储。MapReduce,一种编程模型,方…...
910数据结构(2020年真题)
算法设计题 问题1 现有两个单链表A和B,其中的元素递增有序,在不破坏原链表的情况下,请设计一个算法,求这两个链表的交集,并将结果存放在链表C中。 (1)描述算法的基本设计思想; (2)根据设计思想࿰…...
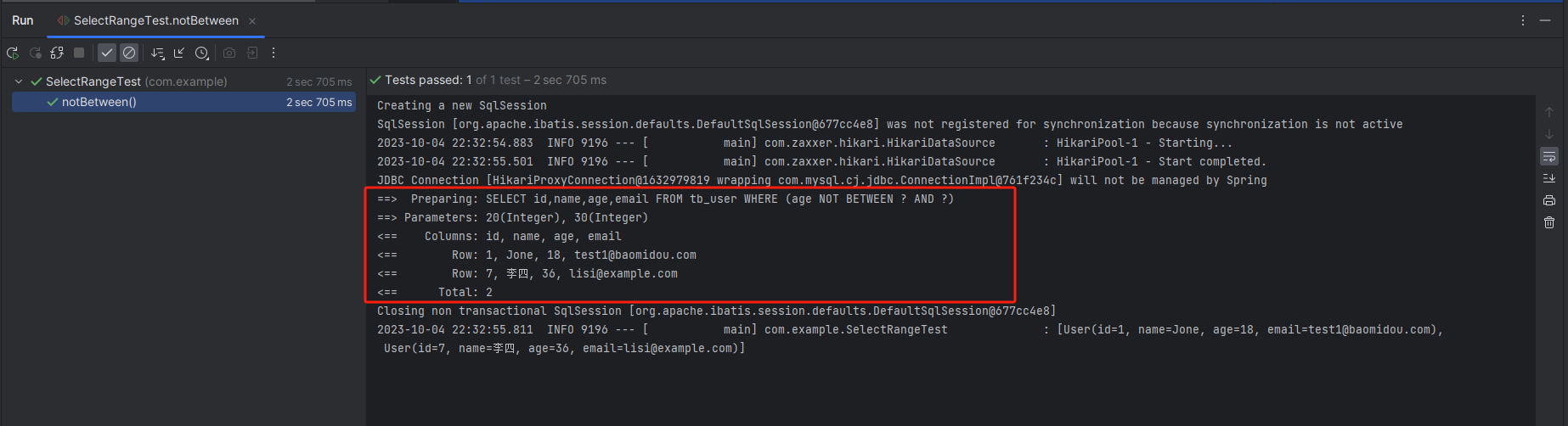
MyBatisPlus(八)范围查询
说明 范围查询,包括: 大于大于等于小于小于等于在范围内在范围外 大于:gt 代码 Testvoid gt() {LambdaQueryWrapper<User> wrapper new LambdaQueryWrapper<>();wrapper.gt(User::getAge, 20);List<User> users mapp…...

【day10.04】QT实现TCP服务器客户端搭建的代码
服务器: #include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this);//实例化一个服务器server new QTcpServer(this);//此时,服务器已经成功进入…...

milvus 结合Thowee 文本转向量 ,新建表,存储,搜索,删除
1.向量数据库科普 【上集】向量数据库技术鉴赏 【下集】向量数据库技术鉴赏 milvus连接 from pymilvus import connections, FieldSchema, CollectionSchema, DataType, Collection, utility connections.connect(host124.****, port19530)2.milvus Thowee 文本转向量 使用 …...
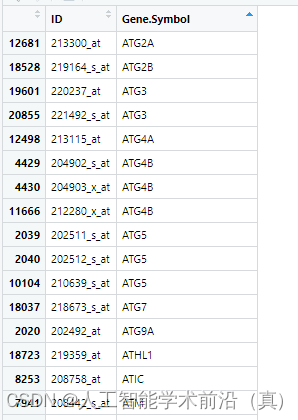
GEO生信数据挖掘(三)芯片探针ID与基因名映射处理
检索到目标数据集后,开始数据挖掘,本文以阿尔兹海默症数据集GSE1297为例 目录 处理一个探针对应多个基因 1.删除该行 2.保留分割符号前面的第一个基因 处理多个探针对应一个基因 详细代码案例一删除法 详细代码案例二 多个基因名时保留第一个基因名…...

力扣 -- 96. 不同的二叉搜索树
解题步骤: 参考代码: class Solution { public:int numTrees(int n) {vector<int> dp(n1);//初始化dp[0]1;//填表for(int i1;i<n;i){for(int j1;j<i;j){//状态转移方程dp[i](dp[j-1]*dp[i-j]);}}//返回值return dp[n];} }; 你学会了吗&…...
)
经典算法-枚举法(百钱买百鸡问题)
题目: 条件:现有 100 元,一共要买公鸡、母鸡、小鸡三种鸡,已知公鸡 5 元一只,母鸡 3 元一只,1 元可以买三只小鸡。 要求:公鸡、母鸡、小鸡都要有,一共买 100 只鸡。有哪几种买法&am…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...
:邮件营销与用户参与度的关键指标优化指南)
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南
精益数据分析(97/126):邮件营销与用户参与度的关键指标优化指南 在数字化营销时代,邮件列表效度、用户参与度和网站性能等指标往往决定着创业公司的增长成败。今天,我们将深入解析邮件打开率、网站可用性、页面参与时…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...

pikachu靶场通关笔记19 SQL注入02-字符型注入(GET)
目录 一、SQL注入 二、字符型SQL注入 三、字符型注入与数字型注入 四、源码分析 五、渗透实战 1、渗透准备 2、SQL注入探测 (1)输入单引号 (2)万能注入语句 3、获取回显列orderby 4、获取数据库名database 5、获取表名…...

6️⃣Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙
Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙 一、前言:离区块链还有多远? 区块链听起来可能遥不可及,似乎是只有密码学专家和资深工程师才能涉足的领域。但事实上,构建一个区块链的核心并不复杂,尤其当你已经掌握了一门系统编程语言,比如 Go。 要真正理解区…...

macOS 终端智能代理检测
🧠 终端智能代理检测:自动判断是否需要设置代理访问 GitHub 在开发中,使用 GitHub 是非常常见的需求。但有时候我们会发现某些命令失败、插件无法更新,例如: fatal: unable to access https://github.com/ohmyzsh/oh…...
