国庆中秋宅家自省: Python在Excel中绘图尝鲜

【一】国庆+中秋: 悟
【国庆+中秋】双节来临,相信各位有自己度过的方式,而我却以独特的方式度过了一个说出来不怕各位见笑的双节; 双节到来,没有太多惊喜,也没有太多的负面情绪, 只是喜欢独处,静静反省这些年走过的酸甜苦辣;生活中的许多不欢而散,不期而遇,不请自来,不三不四,不伦不类到生活的不得已,无奈,有欢有悲,有惊有喜,有得有失,有聚有散........太多的太多,每一个众生有自己诠释生活的方式,如果自觉良好,没什么大不了,自喜自乐,觉得心安理得,自觉生活本该就这样,那好,已经领悟到生活的真谛;恭喜你,已经渡劫成功,祝你生活如愿,所有的愿望不期而遇,所有的美好如愿以偿,生活美满,事事如意;
【国庆+中秋】独坐阳台,独品一杯热茶,遥望天边夕阳........久久凝视,感觉少了点什么,心里有一丝丝惬意,但又有丁丁儿不甘,这种心境难道是生活不如意,欲望太多,自寻烦恼,还是人到中年一事无成的映照,也许这些年走过的点点滴滴太辛酸,自己的期望未成,兴许有多么不如愿,不心甘,走过的岁月没有太多如愿, 曾经默默许下愿望落空, 曾经的激情渐渐暗淡, 曾经的豪言壮语早已抛脑后.........一切的一切.......温水煮青蛙式的生活方式|自律性差|易受周边干扰|无形中迷失自我|难挡生活中太多诱惑|心智不成熟|人格不完善|生活历练不够|认知低下|不擅长提升|做事效率低|许多许多的诱因.........许多的许多.........归于而我消磨于无形中淡忘生活的期望................|终归平凡|碌碌无为|抱憾终身| ...........最后深深感慨: 下辈子再也不来人间......In my next life, I will never come back to earth.........
【二】国庆+中秋: 道
【国庆+中秋】这双节,没有同以往,约上好友,爱人,家人好好聚一聚,一同去旅游,品尝各种美食,好好放松放松;而是独自在家,品读人性弱点,财务自由之旅,职场不是你想的那样,复盘,闭环 思维,金字塔思维,结构化思维,逻辑思维,如何开挂人生,自律3600天后....假如生活欺骗了你,能否给自己救赎的机会.........等等,走过岁月留下不甘后的自我救赎,慢性人生思考,生活思维方式如何固化了自我.......等等 , 想了很多,很多...悟了很多很多, 最终生活一塌糊涂,一地鸡毛,一无是处.......; 悲哀啊.....自我救赎之路..........................
【国庆+中秋】自我不成功,自我不完善,都只能怪自己,没有谁能阻止自我成长革新,所有的不成功都源自于自我革新中缺失太多而不利自我蜕变,量变还没达到质变,懈怠生活.....:余生,构建一套独立运行的思维体系,一套属于自己思维体系,能够独立运行的思维体系,任何不成体系的认知,知识,思维方式.....都终将阻碍自我进步成长;荣登顶峰的顽石..........
【国庆+中秋】阳光之道,大路两边,各走一边: 爱生活,学会: 1000首歌 吉他自由弹唱 净化心灵 提升认知 不断精进 该变则变 ...生活需继续.....静待时机.....厚积簿发......寻自我之道....入慷慨大道.....登泰山之顶......创一家不断造血的公司.....入红尘,顺势而为,利己利他,内在丰盛,外在富足.......内在是因......外在是果.......外在是内在的显化..................悟...修.......... 无遗憾了一生.........
【三】用Excel数据Python绘图
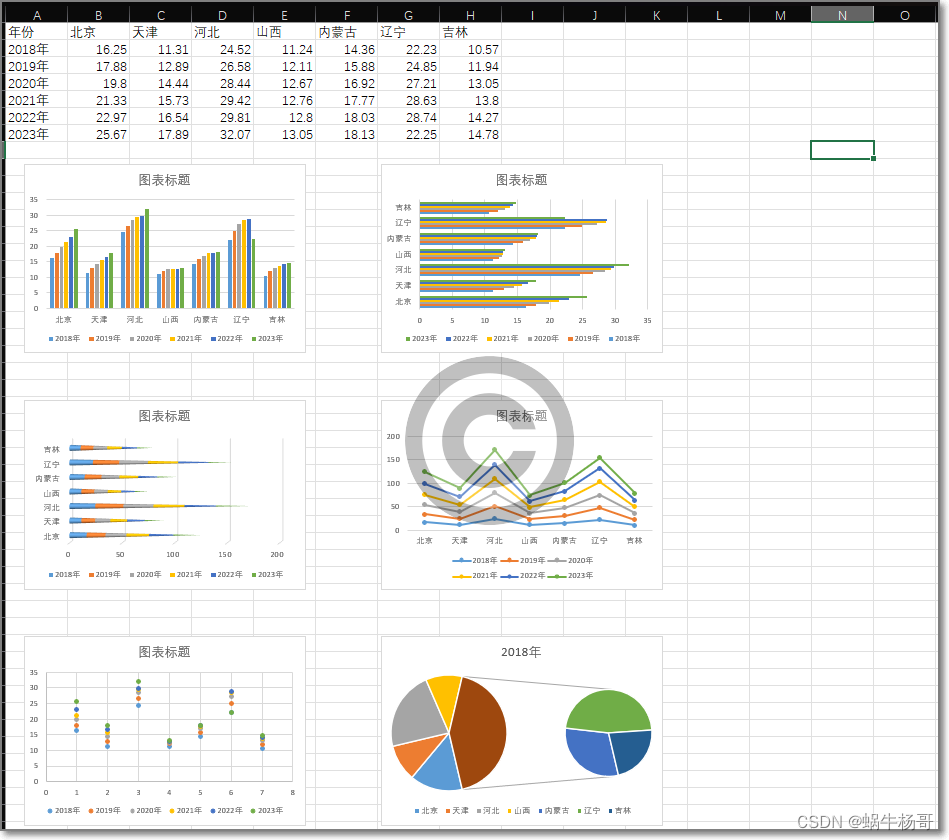
excel表格中的数据:
年份 北京 天津 河北 山西 内蒙古 辽宁 吉林 2018年 16.25 11.31 24.52 11.24 14.36 22.23 10.57 2019年 17.88 12.89 26.58 12.11 15.88 24.85 11.94 2020年 19.8 14.44 28.44 12.67 16.92 27.21 13.05 2021年 21.33 15.73 29.42 12.76 17.77 28.63 13.8 2022年 22.97 16.54 29.81 12.8 18.03 28.74 14.27 2023年 25.67 17.89 32.07 13.05 18.13 22.25 14.78
import xlwings as xw import os'''一份excel表格数据绘制不同的类型图 ''' root = os.getcwd() app = xw.App(visible=True, add_book=False) # 使用相对路径 wb = app.books.open(r"../file/GDP数据.xlsx", read_only=False) sht = wb.sheets(1) sht.api.Range("A1").CurrentRegion.Select() # 数据 sht.api.Shapes.AddChart2(-1, xw.constants.ChartType.xlColumnClustered, 20, 150, 300, 200, True) sht.api.Shapes.AddChart2(-1, xw.constants.ChartType.xlBarClustered, 400, 150, 300, 200, True) sht.api.Shapes.AddChart2(-1, xw.constants.ChartType.xlConeBarStacked, 20, 400, 300, 200, True) sht.api.Shapes.AddChart2(-1, xw.constants.ChartType.xlLineMarkersStacked, 400, 400, 300, 200, True) sht.api.Shapes.AddChart2(-1, xw.constants.ChartType.xlXYScatter, 20, 650, 300, 200, True) sht.api.Shapes.AddChart2(-1, xw.constants.ChartType.xlPieOfPie, 400, 650, 300, 200, True)
运行程序后效果图:
【四】道 法 术 器 势
修行总纲
道
“道”是天道,是最终的真理,囊括整个世界和宇宙的自然法则只可认识不可更改。
道,是价值观范畴。心学大家王阳明说过“天理即人心”,翻译过来就是天理因人而存在的。所谓,天道也是人的认识。人的价值观有不同的层次,人生观就是人生的最高价值观,最终极的道,是宇宙的价值观,宇宙是一个终极生命体。价值观决定了人的思维方法,决定了人们为人处事的原则,价值观也直接决定了一个人的行为方式。话说“道不同不足与谋”,就是说人的价值观不同是无法一起共事的。现在流行的“三观”理论,也是这个意思,人的三观分别指的是人生观、价值观、世界观。三观不正,就是指的人的基本价值观、人生观、世界观是不正的。
三观理论,世界观要排在前头,世界观也叫宇宙观,是人对这个世界的总的看法和根本观点,世界观的基本问题是精神和物质,有两种基本观点,即:“唯物主义世界观”和“唯心主义世界观”。
第二位的是人生观,人生观是对人生的基本看法,对人类生存的目的、价值和意义的基本观点。人生观也同时属于价值观范畴,人生观是由世界观决定的。
排在第三位的是人的价值观,价值观排在世界观和人生观之后,不是因为不重要,而是因为价值观最接地气,是落地的观点,一个人有什么样的价值观,则会有什么样的行为方式,会有什么样的人生。价值观是指人们在认识各种具体事物的价值的基础上,形成的对事物价值的总的看法和根本观点。通俗点讲就是,价值观是你认为什么最宝贵,什么最不值钱。一个人的价值观一旦确定,就不会轻易改变,是相对稳定的。
法
“法”是规则,是原则,是方法论,是“人定”;“术”是技术层面,是具体的方式;“器”是指有型的物质或是有形的工具,“工欲善其事,必先利其器”此中的“器”就是如此;“势”就是当下的时空趋势,地势,情势,形势,权势,说的都是一种时空趋势,一种蕴含的能量。
法,是实现价值观的最根本的方法、法理、原则、思路、方针、战略等。法是在自然规则的运行中寻找和总结出来的一种方法。法是对道的诠释和总结。中国的大部分地区是四季分明的,冬天冷夏天热,在古代没有暖气也没有空调,我们的祖先很聪明,充分认识到这个“天道”,进而在造房子的时候,选择坐南朝北,身体上是冬暖夏凉的。
术
术,是形式,是方式,是技术上的手段。你看“算术”“巫术”“法术”“武术”“权术”等,指的大抵都是这个意思。术在道和法之后,属于下乘。“术”是在规则体系指导下的具体操作方法,只要指导原则不变,具体方法可以千变万化,就是说只要正的“道”带来的“法”不变,“术”是可以在正常的轨道上千变万化,而且万变不离其宗的。术可以通过练习获得,也可以通过对法的推理而产生。
器
器,是工具。工具的作用就是提高效率和把复杂的问题简单化。为了更快,人们发明了汽车,为了管理员工迟到早退,人们发明了打卡机,为了快捷计算,人们发明了计算器。是工具大大提高了我们的生产力,是工具让这个社会飞速发展。可以这么说,“器”是用来体现道的思想的,也是人体器官的延伸,从而简化问题,更快捷达成目标。
势
势,是从“道、法、术、器”体现的势能。势也是一种惯性,是一种发展方向,它本身蕴含着无穷无尽的能量。势,须“顺势”而为,不可以逆势而对。这个世界一眼观去,大抵是由一维、二维、三维物体构成的,同时物理学告诉我们,从点到线,再从线到面,从面到立方体,其实是一个逐级投影而已。三维其实是四维的投影,空间加上时间的轴线,就变成了四维。四维其实就是势的进阶趋势,四维思维是一种对未来的预判。“上下四方曰宇,往古来今曰宙”,天地就是时间和空间的两个坐标系统,时空——宇宙——天地,人是天地间的一粒尘埃而已。势是最后提及,但不是势不重要,《易经》说到“物极必反”“否极泰来”“亢龙有悔”,可见,势是可以翻手为云覆手为雨的。真所谓“三十年河东三十年河西”,势不可挡,来势汹汹啊。
道不易,法简易,术变易,器快易,势趋易。为人处事务必以道为根本,讲究方“法”,注意方式,利用规律,善用工具,巧用技术,势不可挡,达成目标。
相关文章:

国庆中秋宅家自省: Python在Excel中绘图尝鲜
【一】国庆中秋: 悟 【国庆中秋】双节来临,相信各位有自己度过的方式,而我却以独特的方式度过了一个说出来不怕各位见笑的双节; 双节到来,没有太多惊喜,也没有太多的负面情绪, 只是喜欢独处,静静反省这些年走过的酸甜苦辣;生活中的许多不欢而散,不期而遇…...
计算机中的进制转换
在计算机软件中,经常需要进行进制转换,这包括二进制、八进制、十进制和十六进制之间的转换。以下是一些常见的转换方法: 二进制转十进制:这是最直接的转换,基本上不需要什么特别的算法。你只需要按照二进制的权值进行…...

Oracle统计信息问题排查常用SQL
Oracle统计信息问题排查常用SQL 对表的基本情况分析统计信息收集作业分析最近一次的统计信息收集修改触发统计信息收集的阈值 对表的基本情况分析 是否为临时表: select owner,table_name,temporary from dba_tables where table_namexxx;是否为分区表:…...

css圣杯布局和双飞翼布局
圣杯布局 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta http-equiv"X-UA-Compatible" content"IEedge"><meta name"viewport" content"widthdevice-width, in…...

机器学习笔记 - 深入研究spaCy库及其使用技巧
一、简述 spaCy 是一个用于 Python 中高级自然语言处理的开源库。它专为生产用途而设计,这意味着它不仅功能强大,而且快速高效。spaCy 在学术界和工业界广泛用于各种 NLP 任务,例如标记化、词性标注、命名实体识别等。 安装,这里使用阿里的源。 pip install spacy…...

网站强制跳转至国家反诈中心该怎么办?怎么处理?如何解封?
在互联网环境中,网站安全是非常重要的。然而,在实际操作过程中,不少网站可能因内容问题、技术安全漏洞等原因被迫下线甚至跳转至国家反诈骗中心网址。面对这一严峻问题,我们如何有效解决,让网站恢复运行并解除强制跳转…...
2023年10月4日
服务器 #include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this);//实例化一个服务器server new QTcpServer(this);//此时,服务器已经成功进入监听状态&…...
MacBook 录制电脑内部声音
MacBook 录制电脑内部声音 老妈喜欢跳广场舞,现在广场舞音频下载都收费了!没办法,只能自己录歌了,外录有杂音大家也都知道,所以就只能采用内录的方式然后再用 Audition 调整一下音量大小。 一、(前置条件&a…...

mysql主从复制和读写分离
在企业应用中,成熟的业务通常数据量都比较大 单台MySQL在安全性、高可用性和高并发方面都无法满足实际的需求 配置多台主从数据库服务器以实现读写分离 所以要做主从服务器,保证安全性 做一写一读服务器,将提升性能 1、什么是读写分离 …...
【计算机网络】网络层-数据平面(学习笔记)
一、网络层提供的服务 1、虚电路服务 通讯前建立虚电路,发送前认为选择路径,所以分组沿着同一条虚电路。 特点:带宽固定 2、数据报服务 数据可能沿着不同路径传输 3、网络层的两个层面 数据层面:源主机到目标主机 控制层面&…...
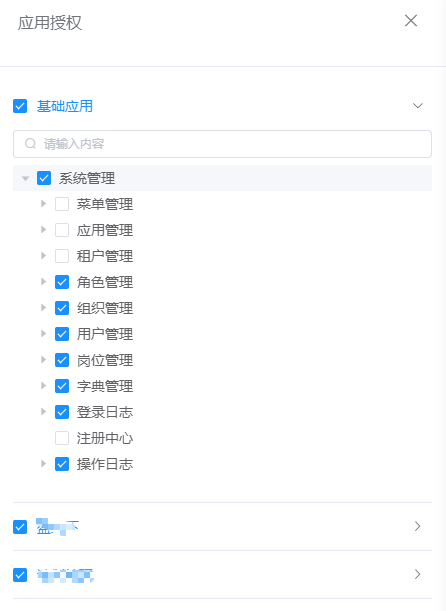
el-collapse 嵌套中 el-checkbox作为标题,选中复选框与el-tree联动
<el-drawertitle"应用授权":visible.sync"menuDrawer"><el-collapse accordion style"padding: 15px"><el-collapse-item v-for"item in platList"><template slot"title"><el-checkbox v-model…...

Ubuntu中还换源 sudo apt-get update更新失败
sudo apt-get update更新失败 1 前提2 编辑3 换源 1 前提 浏览器可以访问百度 如下文章: VMware 中虚拟机没网 2 编辑 输入如下命令,进入换源文件: sudo gedit /etc/apt/sources.list 3 换源 中科大 deb http://mirrors.ustc.edu.cn/ub…...

flutter播放rtmp视频
安装 dependencies:fijkplayer: ^0.11.0使用方法 import package:fijkplayer/fijkplayer.dart; import package:flutter/material.dart;class RtmpPlayerPage extends StatefulWidget {const RtmpPlayerPage({super.key});overrideState<RtmpPlayerPage> createState()…...
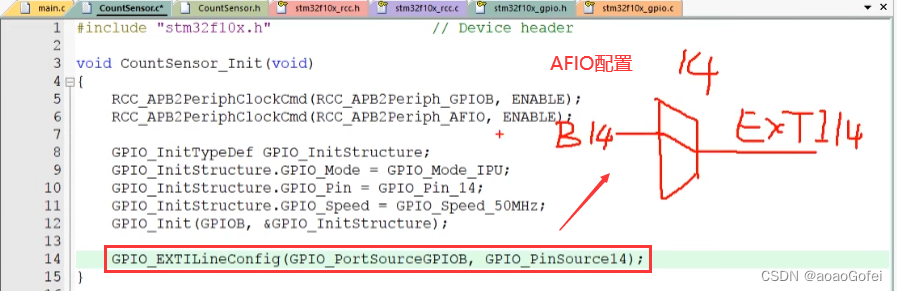
stm32 - 中断
stm32 - 中断 概念中断向量表NVIC 嵌套中断向量控制器优先级 中断EXTI概念基本结构例子- 对射式红外传感器计次例子 - 旋转编码器 概念 stm32 支持的中断资源(都属于外设) EXTITIMADCUSARtSPII2C stm32支持的中断 内核中断 外设中断 中断通道与优先级 一…...

【洛谷 P1216】[USACO1.5] [IOI1994]数字三角形 Number Triangles 题解(动态规划)
[USACO1.5] [IOI1994]数字三角形 Number Triangles 题目描述 观察下面的数字金字塔。 写一个程序来查找从最高点到底部任意处结束的路径,使路径经过数字的和最大。每一步可以走到左下方的点也可以到达右下方的点。 在上面的样例中,从 7 → 3 → 8 →…...
十四天学会C++之第四天(面向对象编程基础)
类和对象是什么? 在C中,类是一种用户定义的数据类型,它可以包含数据成员(也就是属性)和成员函数(也就是方法)。类是一种模板或蓝图,用于创建具体的对象。 对象是类的实例ÿ…...

复习Day09:哈希表part02:141.环形链表、142. 环形链表II、454.四数相加II、383赎金信
之前的blog:https://blog.csdn.net/weixin_43303286/article/details/131765317 我用的方法是在leetcode再过一遍例题,明显会的就复制粘贴,之前没写出来就重写,然后从拓展题目中找题目来写。辅以Labuladong的文章看。然后刷题不用…...

Internet通过TCP/IP协议可以实现多个网络的无缝连接
Internet通过TCP/IP(Transmission Control Protocol/Internet Protocol,传输控制协议/互联网协议)协议实现多个网络的无缝连接。 TCP/IP是Internet的基础通信协议套件,它定义了数据如何在不同网络之间传输和路由,使得…...

互联网Java工程师面试题·Dubbo 篇·第二弹
目录 18、Dubbo 用到哪些设计模式? 19、Dubbo 配置文件是如何加载到 Spring 中的? 20、Dubbo SPI 和 Java SPI 区别? 21、Dubbo 支持分布式事务吗? 22、Dubbo 可以对结果进行缓存吗? 23、服务上线怎么兼容旧版本&…...
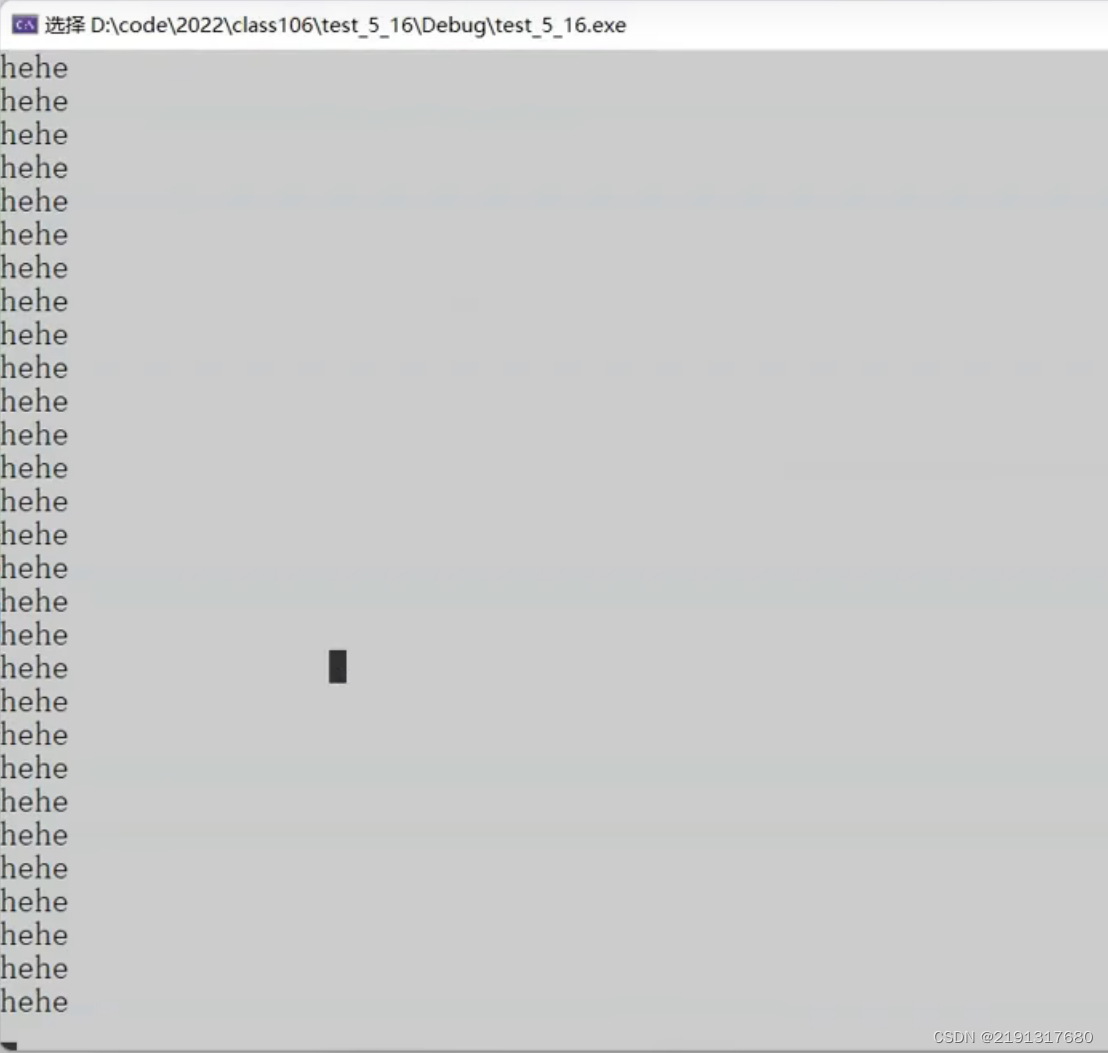
(c语言)经典bug
#include<stdio.h> //经典bug int main() { int i 0; int arr[10] {1,2,3,4,5,6,7,8,9,10}; for (i 0; i < 12; i) //越界访问 { arr[i] 0; printf("hehe\n"); } return 0; } 注:输出结果为死循…...

vscode里如何用git
打开vs终端执行如下: 1 初始化 Git 仓库(如果尚未初始化) git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...
