长剖与贪心+树上反悔贪心:1004T4
长剖的本质是一种贪心。(启发式合并本质也是类似哈夫曼树的过程)
在此题中,首先肯定变直径,然后选端点为根。然后选叶子。而每个叶子为了不重复计算,可以只计算其长剖后所在链的贡献。(本题精髓,用长剖来贪心)
然后钦定某个点必选,就是一种反悔贪心。很显然的思路是删掉排名 2 ∗ k − 1 2*k-1 2∗k−1 的叶子,但考虑:
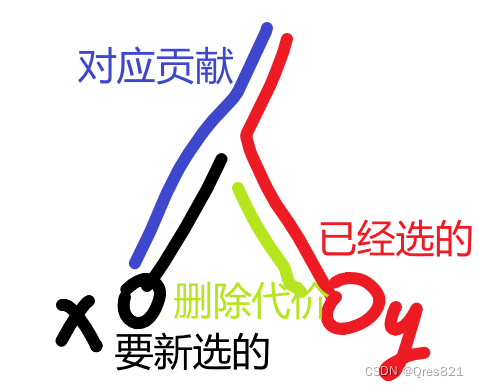
所以需要考虑离其最近被选的点
#include<bits/stdc++.h>
using namespace std;
//#define int long long
inline int read(){int x=0,f=1;char ch=getchar(); while(ch<'0'||
ch>'9'){if(ch=='-')f=-1;ch=getchar();}while(ch>='0'&&ch<='9'){
x=(x<<1)+(x<<3)+(ch^48);ch=getchar();}return x*f;}
#define Z(x) (x)*(x)
#define pb push_back
//mt19937 rand(time(0));
//mt19937_64 rand(time(0));
//srand(time(0));
#define N 500010
//#define M
//#define mo
struct node { int x; long long y, z; };
int n, m, i, j, k, T, p1, p2, in[N];
int u, v, w, qe;
vector<node>G[N]; struct Tree {int i, j, k, rt, mn[N]; long long h[N], mxh[N], mx[N], sum[N]; int son[N], dep[N], top[N]; int f[N][22], rk[N], dfn[N]; node w[N]; void dfs1(int x, int fa, int &p1) {//p1 p2if(h[x]>h[p1]) p1=x; for(auto t : G[x]) {int y=t.y; long long z=t.z; if(y==fa) continue; h[y]=h[x]+z; dfs1(y, x, p1); }}void dfs2(int x, int fa) { //son[x] h[x] dep[x]dep[x]=dep[fa]+1; mx[x]=mxh[x]=h[x]; for(auto t : G[x]) {int y=t.y; long long z=t.z; if(y==fa) continue; h[y]=h[x]+z;
// printf("%lld(%lld) --%lld-> %lld(%lld)\n", x, h[x], z, y, h[y]); dfs2(y, x); mx[x]=max(mx[x], mx[y]); if(mxh[y]>mxh[son[x]]) son[x]=y; }if(son[x]) mxh[x]=mxh[son[x]]; }void dfs3(int x, int fa, int tp) {//top[x] w[x]
// printf("> %d\n", tp); top[x]=tp; f[x][0]=fa; if(in[x]==1 && fa) {w[x].y=h[x]-h[f[top[x]][0]]; w[x].x=x; }for(auto t : G[x]) {int y=t.y; if(y==fa) continue; if(y==son[x]) dfs3(y, x, tp); else dfs3(y, x, y); }}void init() {
// for(i=1; i<=n; ++i) printf("%d ", top[i]); printf("\n");
// for(i=1; i<=n; ++i) printf("%d ", h[i]); printf("\n"); sort(w+1, w+n+1, [] (node x, node y) { return x.y<y.y; }) ; reverse(w+1, w+n+1); for(i=1; i<=n; ++i) {
// printf("%lld(%lld) ", w[i].y, w[i].x); if(w[i].x) sum[i]=w[i].y, rk[w[i].x]=i, dfn[i]=w[i].x; sum[i]+=sum[i-1]; }
// printf("\n"); for(k=1; k<=19; ++k) for(i=1; i<=n; ++i) f[i][k]=f[f[i][k-1]][k-1]; }void dfs4(int x, int fa) {if(in[x]==1 && fa) mn[x]=rk[x]; else mn[x]=1e9; for(auto t : G[x]) {int y=t.y, z=t.z; if(y==fa) continue; dfs4(y, x); mn[x]=min(mn[x], mn[y]); //排名最小 }}int tiao(int x, int g) {for(k=19; k>=0; --k)if(mn[f[x][k]]>g) x=f[x][k]; return f[x][0]; }int lca(int x, int y) {if(x==y) return x; if(dep[x]<dep[y]) swap(x, y); for(int k=19; k>=0; --k)if(dep[f[x][k]]>=dep[y]) x=f[x][k]; if(x==y) return x; for(int k=19; k>=0; --k)if(f[x][k]!=f[y][k]) x=f[x][k], y=f[y][k]; return f[x][0]; }long long calc(int y, int oldy, int newx) {
// printf("Lca(%d %d) : %d\n", oldy, newx, lca(oldy, newx));
// return min(w[mn[y]].y, h[oldy]-h[lca(oldy, newx)]); return min(w[mn[y]].y, h[oldy]-h[y]); }long long que(int x, int k) {if(k==1) {
// int y=dfn[mn[x]]; return h[y]; return mx[x]; }if(mn[x]<=2*k-1) {return sum[min(2*k-1, n)]; }int y=tiao(x, 2*k-1), newx, oldy; long long ans; newx=dfn[mn[x]]; oldy=dfn[mn[y]];
// printf("%d | %d %d %d %d\n", y, newx, oldy, (h[newx]-h[y]), calc(y, oldy, newx)); ans=sum[2*k-1]-calc(y, oldy, newx)+(h[newx]-h[y]); ans=max(ans, sum[2*k-1]-w[2*k-1].y+(h[newx]-h[y])); return ans; }
}T1, T2;void print(long long x) {if(x) print(x/10), putchar(x%10+'0');
}signed main()
{
// freopen("in.txt", "r", stdin);
// freopen("out.txt", "w", stdout);freopen("bomb.in", "r", stdin);freopen("bomb.out", "w", stdout);
// T=read();
// while(T--) {
//
// }n=read(); qe=read(); for(i=1; i<n; ++i) {u=read(); v=read(); w=read(); G[u].pb({u, v, w}); G[v].pb({v, u, w}); ++in[u]; ++in[v]; }T1.h[1]=0; T1.dfs1(1, 0, p1); T1.h[p1]=0; T1.dfs1(p1, 0, p2);T1.rt=p1; T2.rt=p2; T1.h[p1]=0; T1.dfs2(p1, 0); T2.h[p2]=0; T2.dfs2(p2, 0);
// printf("%d %d\n", p1, p2); T1.dfs3(p1, 0, p1); T2.dfs3(p2, 0, p2); T1.init(); T2.init(); T1.dfs4(p1, 0); T2.dfs4(p2, 0); while(qe--) {u=read(); k=read(); print(max(T1.que(u, k), T2.que(u, k))); puts(""); }return 0;
}相关文章:

长剖与贪心+树上反悔贪心:1004T4
长剖的本质是一种贪心。(启发式合并本质也是类似哈夫曼树的过程) 在此题中,首先肯定变直径,然后选端点为根。然后选叶子。而每个叶子为了不重复计算,可以只计算其长剖后所在链的贡献。(本题精髓࿰…...

二叉树经典例题
前言: 本文主要讲解了关于二叉树的简单经典的例题。 因为二叉树的特性,所以关于二叉树的大部分题目,需要利用分治的思想去递归解决问题。 分治思想: 把大问题化简成小问题(根节点、左子树、右子树)&…...

什么是指针的指针和指向函数的指针?
理解指针的指针和指向函数的指针对于C语言初学者来说可能会有些挑战,但它们都是非常重要的概念,可以帮助你更好地理解和利用C语言的强大功能。在本文中,我将详细解释这两个概念,包括它们的概念、用途和示例。 指针的指针…...
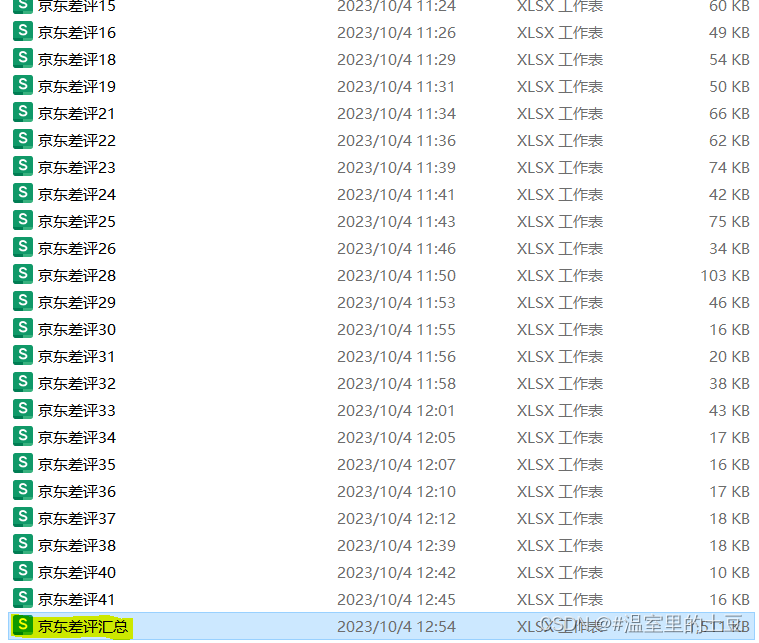
多个excel合并
目的:将同一个文件下的多个 “京东差评.xlsx” 合并为一个:“京东汇总.xlsx" 代码如下: # -*- coding: utf-8 -*- """ Created on Wed Oct 4 12:52:32 2023author: 64884 """import pandas as pd impor…...
Integrity Plus for Mac,保障网站链接无忧之选
在如今数字化的时代,网站链接的完整性对于用户体验和搜索引擎排名至关重要。如果您是一位网站管理员或者经常需要检查网站链接的人,那么Integrity Plus for Mac(Integrity Plus)将成为您最好的伙伴。 Integrity Plus是一款专业的…...

C#,数值计算——Sobol拟随机序列的计算方法与源程序
1 文本格式 using System; using System.Collections.Generic; namespace Legalsoft.Truffer { /// <summary> /// Sobol quasi-random sequence /// </summary> public class Sobol { public Sobol() { } public static void sobseq(int n,…...

以太网协议介绍(ARP、UDP、ICMP、IP)
以太网协议介绍 一、ARP协议 请求: 应答: ARP协议: 0x0001 0x0800 6 4硬件类型:2个字节,arp协议不仅能在以太网上运行还能在其他类型的硬件上运行。以太网用1来表示; 协议类型:两字节。指的是a…...

【C++】STL详解(十)—— 用红黑树封装map和set
📝个人主页:Sherry的成长之路 🏠学习社区:Sherry的成长之路(个人社区) 📖专栏链接:C学习 🎯长路漫漫浩浩,万事皆有期待 上一篇博客:【C】STL…...

Android学习之路(17) Android Adapter详解
Adapter基础讲解 本节引言 从本节开始我们要讲的UI控件都是跟Adapter(适配器)打交道的,了解并学会使用这个Adapter很重要, Adapter是用来帮助填充数据的中间桥梁,简单点说就是:将各种数据以合适的形式显示到view上,提供 给用户看…...

实验室超声波萃取技术的原理和特点是什么?
梵英超声(fanyingsonic)实验室超声波清洗机 超声波萃取中药材的优越性源于超声波的特殊物理性质。通过压电换能器产生的快速机械振动波,超声波可减少目标萃取物与样品基体之间的作用力,从而实现固液萃取分离。 (1)加速介质质点运…...

用Python操作Word文档,看这一篇就对了!
本文主要讲解Python中操作word的思路。 一、Hello,world! 使用win32com需要安装pypiwin32 pip install pypiwin32 推荐使用python的IDLE,交互方便 1、如何新建文档 from win32com.client import Dispatchapp Dispatch(Word.Application…...

力扣 -- 879. 盈利计划(二维费用的背包问题)
解题步骤: 参考代码: 未优化的代码: class Solution { public:int profitableSchemes(int n, int minProfit, vector<int>& group, vector<int>& profit) {//计划数int lengroup.size();//每一维都多开一行空间vector&…...

虚拟机的三种网络连接模式
文章目录 桥接模式NAT模式主机模式 桥接模式 虚拟系统占用主机网段中的一个IP地址,可以正常上网 NAT模式 主机生成一个非本主机的网段的IP的网卡,同时虚拟系统中使用一个该网段的IP地质,网络数据能通过主机的网卡来代理发送出去࿰…...

SQL调优
# 插入数据 页合并 # order by优化 视频教程:34. 进阶-SQL优化-order by优化_哔哩哔哩_bilibili 在创建索引的时候,如果没有设置顺序,是会默认升序的;但phone想要倒序,则需要额外的排序 根据需要,创建联合…...

python写一个开机启动的选项
创建一个Python脚本,以便用户可以选择在开机时启动它,可以使用pyautogui库来创建一个简单的交互式界面,其中用户可以选择是否将程序添加到开机启动项中 import pyautogui import osdef add_to_startup():# 提示用户选择是否要在开机时启动程序…...

1500*A. Boredom(DP)
Problem - 455A - Codeforces Boredom - 洛谷 解析: 首先统计每个数的个数,并且统计出最大值mx。 问题转换为,从1-mx 中选择任意个数字,使其都不相邻,求最大的总和。 开始没有思路,以为直接选取偶数位和奇…...

小程序关键词排名:优化你的应用在搜索中的地位
曾经,我们沉浸在应用商店的浩瀚海洋中,寻找着那个能够满足我们需求的小程序。而今,作为开发者,你的小程序究竟能否在这个无边的数字海洋中引起更多涟漪呢?故事的开始,恰巧就在这个问题的探寻中。让我们携手…...

OpenGLES:3D立方体纹理贴图
效果展示 一.概述 前几篇博文讲解了OpenGLES绘制多种3D图形,并赋予丰富的色彩,但是在这些3D图形绘制过程中,有一点还没有涉及,就是纹理贴图。 今天这篇博文我会用如下六张图片对立方体进行纹理贴图,实现六个面都是贴…...

线程的概述
#include <pthread.h> int pthread_create(pthread_t *thread, const pthread_attr_t *attr, void *(*start_routine) (void *), void *arg); 功能:创建一个子线程 参数: -thread:传出参数,线程创建成功后,子线程的ID被写到…...

竞赛选题 机器视觉目标检测 - opencv 深度学习
文章目录 0 前言2 目标检测概念3 目标分类、定位、检测示例4 传统目标检测5 两类目标检测算法5.1 相关研究5.1.1 选择性搜索5.1.2 OverFeat 5.2 基于区域提名的方法5.2.1 R-CNN5.2.2 SPP-net5.2.3 Fast R-CNN 5.3 端到端的方法YOLOSSD 6 人体检测结果7 最后 0 前言 ǵ…...

【网络】每天掌握一个Linux命令 - iftop
在Linux系统中,iftop是网络管理的得力助手,能实时监控网络流量、连接情况等,帮助排查网络异常。接下来从多方面详细介绍它。 目录 【网络】每天掌握一个Linux命令 - iftop工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...
