数据结构与算法系列-二分查找
二分查找
什么是二分查找?
二分查找是一种针对有序集合,每次将要查找的区间缩小一半,直到找到查找元素,或区间被缩小为0。
如何实现二分查找?
实现有3个注意点:
- 终止条件是 low <= high
2.求中点的算法是 low + (high - low)/2
3.low和high的更新是low=mid+1 即到更大的区间找, high=mid-1 即到更小的区间找。
非递归实现
// 终止条件low>=high 当low=high时,mid=low+(high-low)/2=low=high,即没有等号将少比较一个点// 中点 mid = low + (high-low)/2 即以low为起点,计算low和high之间的中点// mid<value 找大区间 low=mid+1,mid>value,找小区间,high=mid-1public int binSearch(int[] arr,int n,int value){int low=0;int high=n-1;while(low<=high){int mid=low+((high-low)>>1);//int mid=low+(high-low)/2;if(arr[mid]<value){low=mid+1;} else if(arr[mid]>value){high=mid-1;} else{return mid;}}return -1;}
递归实现
// 二分查找的递归实现
public int bsearch(int[] a, int n, int val) {return bsearchInternally(a, 0, n - 1, val);
}private int bsearchInternally(int[] a, int low, int high, int value) {if (low > high) return -1;int mid = low + ((high - low) >> 1);if (a[mid] == value) {return mid;} else if (a[mid] < value) {return bsearchInternally(a, mid+1, high, value);} else {return bsearchInternally(a, low, mid-1, value);}
}
二分查找有哪些局限性?
1. 二分查找依赖的是顺序表结构,也就是数组
2. 二分查找要求数据有序
3. 数据量太小不适合二分查找,除非每个数据的操作非常耗时,比如,数组中存储的都是长度超过 300 的字符串,如此长的两个字符串之间比对大小,就会非常耗时。
4. 数据量太大也不适合二分查找,因为数组需要占用大量连续的空间
5. 动态数据不适合二分查找,频繁的插入和删除在数组结构下效率很低
思考题
- 如何编程实现“求一个数的平方根”?要求精确到小数点后 6 位。
可以用牛顿弦切法来求平方跟
double number = 2; //待求平方根的数
double xini = 10;//初始点
while(xinixini - number > 1e-6) {
xini = (number + xinixini)/2/xini;
}
// xini为平方根 - 我刚才说了,如果数据使用链表存储,二分查找的时间复杂就会变得很高,那查找的时间复杂度究竟是多少呢?
链表不像数组那样支持随机访问,所以链表主要花的是查找第n个节点的访问的时间。
第一次需要遍历n/2个节点,
第二次需要遍历n/4个节点,
第三次需要遍历n/8个节点,
n/2 + n/4 + n/8 + …
和约等于n,因此算法复杂度为O(n),单考虑到其他二分查找的额外操作,会比直接遍历循环查找慢一些。
二分查找有哪些变体问题?
对于有序数组中有重复元素而言二分查找通常有以下4个变体问题。
查找第一个值等于给定值的元素
查找最后一个值等于给定值的元素
查找第一个大于等于给定值的元素
查找最后一个小于等于给定值的元素
这些都是查找等于给定值的变体问题,想一想,你有什么思路可以实现呢?
如何实现变体的二分查找?
arr[mid]和value的值的比较有三种情况:大于,小于,等于
那对于问题1和2而言我们要特殊处理的等于的情况,
问题3要特殊处理大于等于的情况,
问题4要特殊处理小于等于的情况。
问题1的特殊处理逻辑:
等于的情况下,我们mid的下标有可能是0,即数组的第一个元素,那么我们直接返回mid就好了,
那其余情况就是mid>0,那么我们就看mid的前一个元素是否等于value,如果不等于,说明mid是第一个等于value的元素,也直接返回,
如果等于mid,那么我们就需要在前面的区间去查找了,即 high = mid - 1;
那问题2,3,4和1的处理思路类似,可以试着自己实现。
1
public int binSearchFirst(int[] arr,int n,int value){int low=0;int high=n-1;while (low<=high) {int mid = low + (high - low) / 2;if(arr[mid]<value){low=mid+1;} else if(arr[mid]>value){high=mid-1;} else{// 需要特殊处理的是等于的情况// 1.看mid是否为第一个元素,是返回mid// 2.看mid的前一个元素是否等于value,不等于返回mid// 3.mid的前一个元素等于value,那么就应该去前面区间找,即 high = mid - 1;if(mid==0||arr[mid-1]!=value) {return mid;}high=mid-1;}}return -1;}
2
public int binSearchFirst(int[] arr,int n,int value){int low=0;int high=n-1;while (low<=high) {int mid = low + (high - low) / 2;if(arr[mid]<value){low=mid+1;} else if(arr[mid]>value){high=mid-1;} else{// 需要特殊处理的是等于的情况// 1.看是mid否为最后一个元素,是返回mid// 2.看mid的后一个元素是否等于value,不等于返回mid// 3.mid的后一个元素等于value,那么就应该去后面区间找,即 low = mid + 1;if(mid==n-1||arr[mid+1]!=value) {return mid;}low=mid+1;}}return -1;}
3
public int binSearchFirst(int[] arr,int n,int value) {int low = 0;int high = n - 1;while (low <= high) {int mid = low + (high - low) / 2;if (arr[mid] >= value) {// 主要处理大于等于的情况// 1.看mid是否为第一个元素,是返回mid// 2.看mid的前一个元素是否小于value,是返回mid// 3.前一个元素大于等于value,应该去前面区间找,即high=mid-1if(mid==0||arr[mid-1]<value){return mid;}high = mid - 1;} else {low = mid + 1;}}return -1;}
4
public int binSearchFirst(int[] arr,int n,int value) {int low = 0;int high = n - 1;while (low <= high) {int mid = low + (high - low) / 2;if (arr[mid] <= value) {// 主要处理大于等于的情况// 1.看mid是否为最后一个元素,是返回mid// 2.看mid的后一个元素是否大于value,是返回mid// 3.后一个元素小于等于value,应该去后面区间找,即low=mid+1if(mid==n-1||arr[mid+1]>value){return mid;}low = mid + 1;} else {high = mid - 1;}}return -1;}
二分查找的实际应用场景?
绝大部分情况能用二分查找解决的问题我们更倾向使用散列表或二叉查找树,
那二分查找其实更适用于近似的查找(范围查找)问题,因为这类问题用上述数据结构都不容易实现。
思考题
我们今天讲的都是非常规的二分查找问题,今天的思考题也是一个非常规的二分查找问题。如果有序数组是一个循环有序数组,比如 4,5,6,1,2,3。针对这种情况,如何实现一个求“值等于给定值”的二分查找算法呢?
我们发现循环数组存在一个性质:以数组中间点为分区,会将数组分成一个有序数组和一个循环有序数组。
如果首元素小于 mid,说明前半部分是有序的,后半部分是循环有序数组;
如果首元素大于 mid,说明后半部分是有序的,前半部分是循环有序的数组;
如果目标元素在有序数组范围中,使用二分查找;
如果目标元素在循环有序数组中,设定数组边界后,使用以上方法继续查找。
时间复杂度为 O(logN)。
相关文章:

数据结构与算法系列-二分查找
二分查找 什么是二分查找? 二分查找是一种针对有序集合,每次将要查找的区间缩小一半,直到找到查找元素,或区间被缩小为0。 如何实现二分查找? 实现有3个注意点: 终止条件是 low < high 2.求中点的算…...

CSS 毛玻璃特效运用目录
主要是记录毛玻璃相关的特效实践案例和实现思路。 章节名称完成度难度文章地址完整代码下载地址Glassmorphism 登录表单完成一般文章链接代码下载Glassmorphism 按钮悬停效果完成一般文章链接代码下载Glassmorphism 计算器完成一般文章链接代码下载Glassmorphism 卡片悬停效果…...
如何在Qt6中引入Network模块
2023年10月1日,周日凌晨 2023年10月2日,周一下午 第一次更新 目录 如果用的是CMakeQt Console ApplicationQt Widgets Application如果用的是qmake 如果用的是CMake find_package(Qt6 COMPONENTS Network REQUIRED) target_link_libraries(mytarget…...

2023/10/4 QT实现TCP服务器客户端搭建
服务器端: 头文件 #ifndef WIDGET_H #define WIDGET_H#include <QWidget> #include <QTcpServer> #include <QTcpSocket> #include <QList> #include <QMessageBox> #include <QDebug>QT_BEGIN_NAMESPACE namespace Ui { cla…...
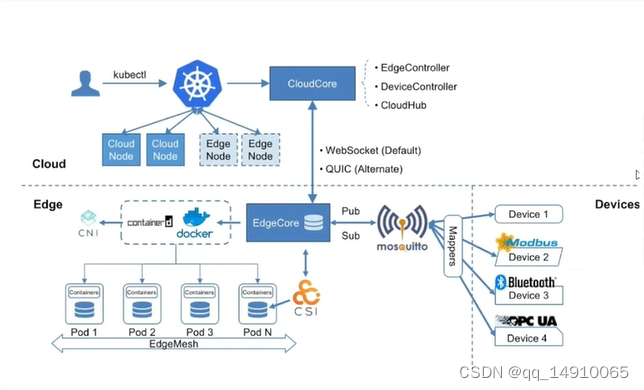
云原生边缘计算KubeEdge安装配置
1. K8S集群部署,可以参考如下博客 请安装k8s集群,centos安装k8s集群 请安装k8s集群,ubuntu安装k8s集群 2.安装kubEedge 2.1 编辑kube-proxy使用ipvs代理 kubectl edit configmaps kube-proxy -n kube-system #修改kube-proxy#大约在40多行…...
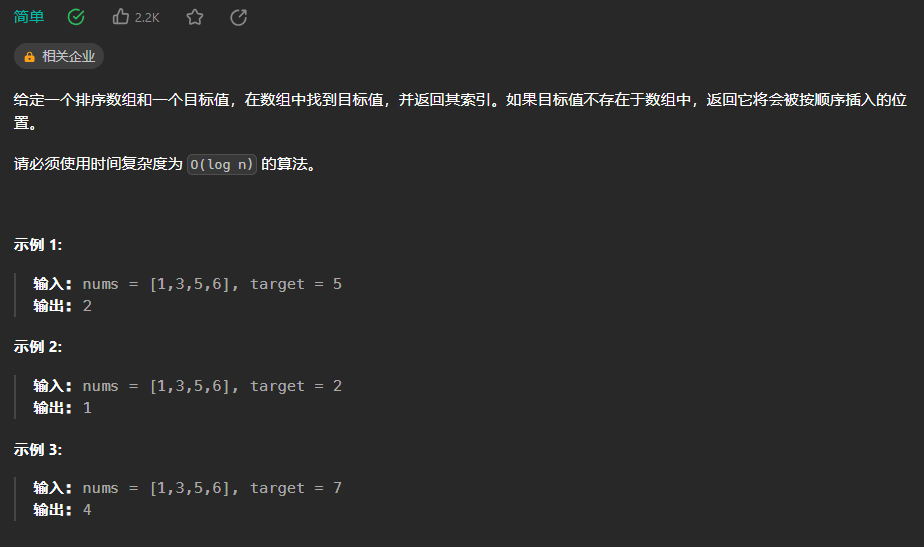
【LeetCode热题100】--35.搜索插入位置
35.搜索插入位置 使用二分查找: class Solution {public int searchInsert(int[] nums, int target) {int low 0,high nums.length -1;while(low < high){//注意每次循环完都要计算midint mid (low high)/2;if(nums[mid] target){return mid;}if(nums[mid]…...

mysql面试题13:MySQL中什么是异步复制?底层实现?
该文章专注于面试,面试只要回答关键点即可,不需要对框架有非常深入的回答,如果你想应付面试,是足够了,抓住关键点 面试官:讲一讲mysql中什么是异步复制?底层实现? MySQL中的异步复制(Asynchronous Replication)是一种复制模式,主服务器将数据写入二进制日志后,无…...
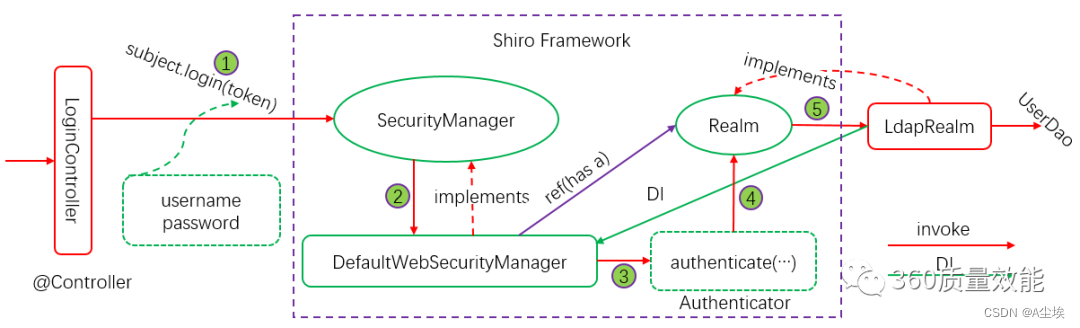
SpringBoot-Shiro安全权限框架
Apache Shiro是一个强大而灵活的开源安全框架,它干净利落地处理身份认证,授权,企业会话管理和加密。 官网: http://shiro.apache.org/ 源码: https://github.com/apache/shiro Subject:代表当前用户或…...

PostgreSQL基础语法
当谈到关系型数据库管理系统(RDBMS)时,PostgreSQL是一个备受推崇的选择。它是一个开源的、强大的RDBMS,具有广泛的功能和支持。本文将介绍一些PostgreSQL的基础语法,以帮助您入门。 1. 安装和配置 在开始使用PostgreS…...

编程前置:处理Excel表格,定位单元格位置,输入文字前,让AI机器人知道我说什么
原提问: input输入表头 (input内除了/,空格 回车 标点符号等 全部作为单元格分隔符) 由我设置input输入的是行or列 给选项 1. 行 2. 列 默认回车或没输入值是列由我设置起始位置行列 例如 3,2 表示3行2列 当我输入3,2 就表示在第…...

Linux基本指令介绍系列第四篇
文章目录 前言一、Linux基本指令介绍1、more指令2、less指令3、head指令4、tail指令5、bc指令6、管道文件介绍7、与时间相关的指令 总结 前言 本文介绍Linux使用时的部分指令,读者如果想了解更多基本指令的使用,可以关注博主的后续的文章。 博主使用的实…...

读取vivo手机截图尺寸移动.jpg等文件
这个代码的设计初衷是为了解决图片处理过程中的一些痛点。想象一下,我们都曾遇到过这样的情况:相机拍摄出来的照片、网络下载的图片,尺寸五花八门,大小不一。而我们又渴望将它们整理成一套拥有统一尺寸的图片,让它们更…...
)
Web前端-Vue2+Vue3基础入门到实战项目-Day2(指令补充, computed计算属性, watch侦听器, 水果购物车)
Web前端-Vue2Vue3基础入门到实战项目-Day2 指令补充指令修饰符v-bind 对样式控制的增强控制class案例 - 京东秒杀tab导航高亮控制style案例 - 控制进度条 v-model 应用于其他表单元素 computed计算属性基本使用computed计算属性 vs methods方法计算属性完整写法案例 - 成绩 wat…...

ffmpeg之去除视频水印
ffmpeg去除水印使用delogo视频滤镜。 delogo参数: x,y,w,h分别表示logo区域的左上角位置及宽度和高度; show:0表示不显示logo区域,1表示显示logo区域。 执行下面的命令: ffmpeg -i 1.mp4 -vf delogox300:y10:w80:h30:show0 out.mp4 效果…...
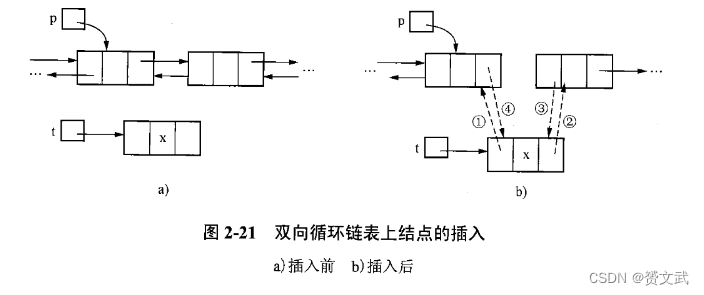
第二章 线性表
线性表 线性表的基本概念线性表的顺序存储线性表顺序存储的类型定义线性表基本运算在顺序表上的实现顺序表实现算法的分析 线性表的链接存储单链表的类型定义线性表的基本运算在单链表上的实现 其他运算在单链表上的实现建表删除重复结点 其他链表循环链表双向循环链表 顺序实现…...

Java 超高频常见字符操作【建议收藏】
文章目录 前言1. 字符串拼接2. 字符串查找3. 字符串截取4. 字符串替換5. 字符串分割6. 字符串比较7. 字符串格式化8. 字符串空格处理 总结 前言 为了巩固所学的知识,作者尝试着开始发布一些学习笔记类的博客,方便日后回顾。当然,如果能帮到一…...
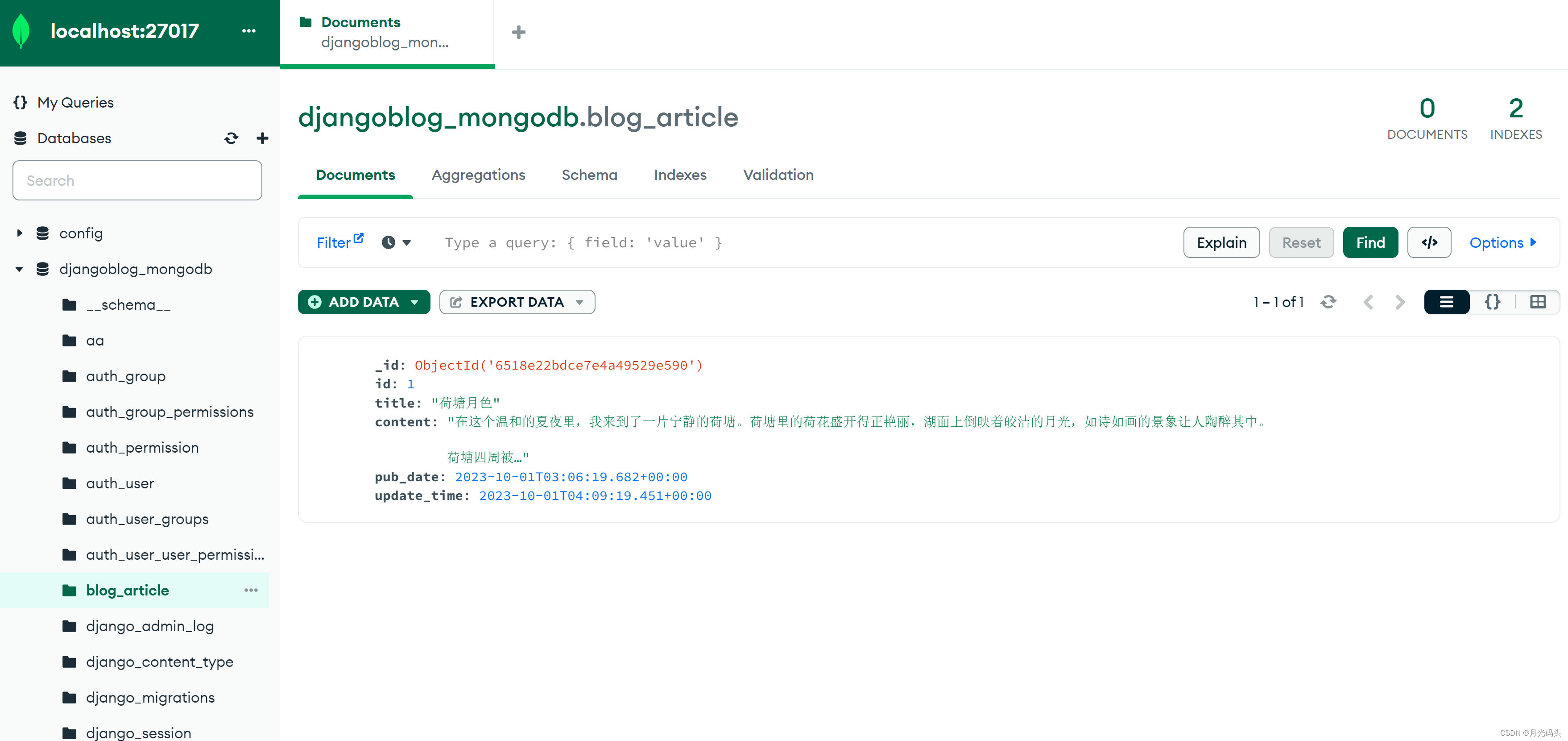
MongoDB数据库网站网页实例-编程语言Python+Django
程序示例精选 PythonDjangoMongoDB数据库网站网页实例 如需安装运行环境或远程调试,见文章底部个人QQ名片,由专业技术人员远程协助! 前言 这篇博客针对《PythonDjangoMongoDB数据库网站网页实例》编写代码,代码整洁,…...
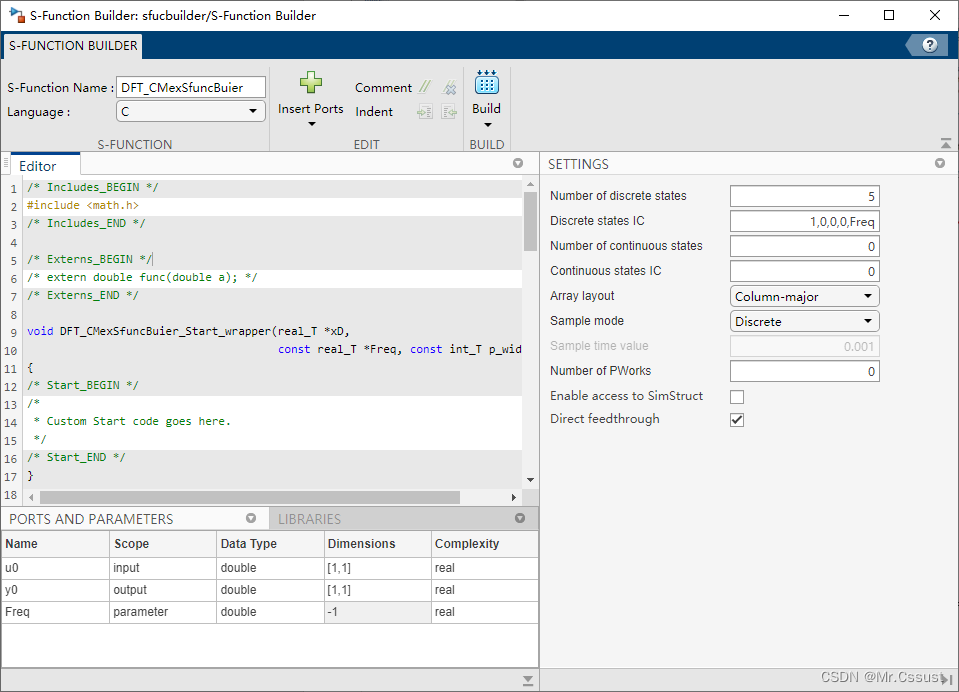
开箱报告,Simulink Toolbox库模块使用指南(七)——S-Fuction Builter模块
S-Fuction Builter S-Fuction Builter模块,Mathworks官方Help对该部分内容的说明如下所示。 DFT算法的原理讲解和模块开发在前几篇文章中已经完成了,本文介绍如何使用S-Fuction Builter模块一步到位地自动开发DFT算法模块,包括建立C MEX S-Fu…...

spring-boot 操作 mongodb 数据库
如何使用 spring-boot 操作 mongodb 数据库 配置文件: spring:data:mongodb:host: 127.0.0.1database: fly_articleDbport: 27017# 可以采取 mysql 写法# uri: mongodb://127.0.0.1/fly_articleDb依赖信息: <?xml version"1.0" encoding"UTF-…...
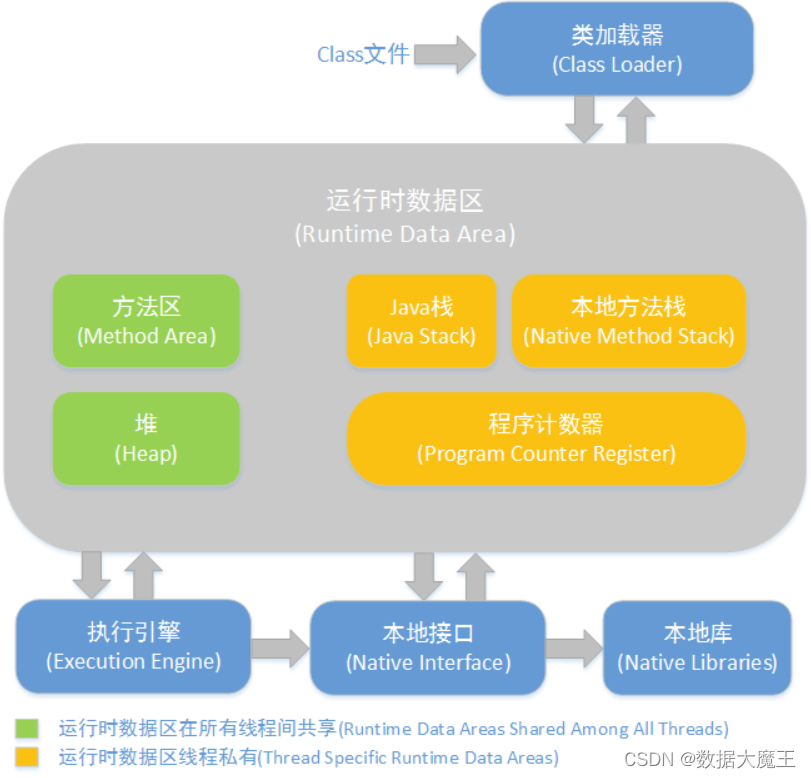
JVM篇---第三篇
系列文章目录 文章目录 系列文章目录一、什么是Java虚拟机?为什么Java被称作是“平台无关的编程语言”?二、Java内存结构三、说说对象分配规则一、什么是Java虚拟机?为什么Java被称作是“平台无关的编程语言”? Java虚拟机是一个可以执行Java字节码的虚拟机进程。Java源文…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

linux arm系统烧录
1、打开瑞芯微程序 2、按住linux arm 的 recover按键 插入电源 3、当瑞芯微检测到有设备 4、松开recover按键 5、选择升级固件 6、点击固件选择本地刷机的linux arm 镜像 7、点击升级 (忘了有没有这步了 估计有) 刷机程序 和 镜像 就不提供了。要刷的时…...

江苏艾立泰跨国资源接力:废料变黄金的绿色供应链革命
在华东塑料包装行业面临限塑令深度调整的背景下,江苏艾立泰以一场跨国资源接力的创新实践,重新定义了绿色供应链的边界。 跨国回收网络:废料变黄金的全球棋局 艾立泰在欧洲、东南亚建立再生塑料回收点,将海外废弃包装箱通过标准…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...
