P1843 奶牛晒衣服 【贪心】
P1843 奶牛晒衣服 【贪心】
题目背景
熊大妈决定给每个牛宝宝都穿上可爱的婴儿装 。但是由于衣服很湿,为牛宝宝晒衣服就成了很不爽的事情。于是,熊大妈请你(奶牛)帮助她完成这个重任。
题目描述
一件衣服在自然条件下用一秒的时间可以晒干 aa 点湿度。抠门的熊大妈只买了一台烘衣机 。使用用一秒烘衣机可以让一件衣服额外烘干 b 点湿度(一秒晒干 a+b 湿度),但在同一时间内只能烘一件衣服。现在有 n 件衣服,第 i 衣服的湿度为 wi (保证互不相同),要你求出弄干所有衣服的最少时间(湿度为 0 为干 )。
输入格式
第一行三个整数,分别为 n,a,b。
接下来 2 到 n+1 行,第 i 行输入 wi 。
输出格式
一行,弄干所有衣服的最少时间。
输入输出样例
输入 #1
3 2 1
1
2
3
输出 #1
1
输入 #2
4 2 3
8 5 7 9
输出 #2
3
说明/提示
样例解释
让机器烘第三件衣服即可一秒完成。
数据范围
1≤wi ,a,b,n≤5×10^5
贪心算法操作过程:
- 最少时间取决于最后一件被弄干的衣服的时间。
- 每次找出剩余的湿度最大的衣服,使用烘干机。
- 用大根堆维护衣服的剩余湿度。
- 时间复杂度为O(nlogn)。
#include <bits/stdc++.h>
using namespace std;
int n,a,b;
int main()
{ cin>>n>>a>>b;priority_queue<int> q;for(int i=1,x;i<=n;i++){cin>>x;q.push(x);}int tpx=q.top();q.pop();int res=0;while(tpx>res*a){res++;q.push(tpx-b);tpx=q.top();q.pop();}cout<<res;return 0;
}相关文章:

P1843 奶牛晒衣服 【贪心】
P1843 奶牛晒衣服 【贪心】 题目背景 熊大妈决定给每个牛宝宝都穿上可爱的婴儿装 。但是由于衣服很湿,为牛宝宝晒衣服就成了很不爽的事情。于是,熊大妈请你(奶牛)帮助她完成这个重任。 题目描述 一件衣服在自然条件下用一秒的时间…...
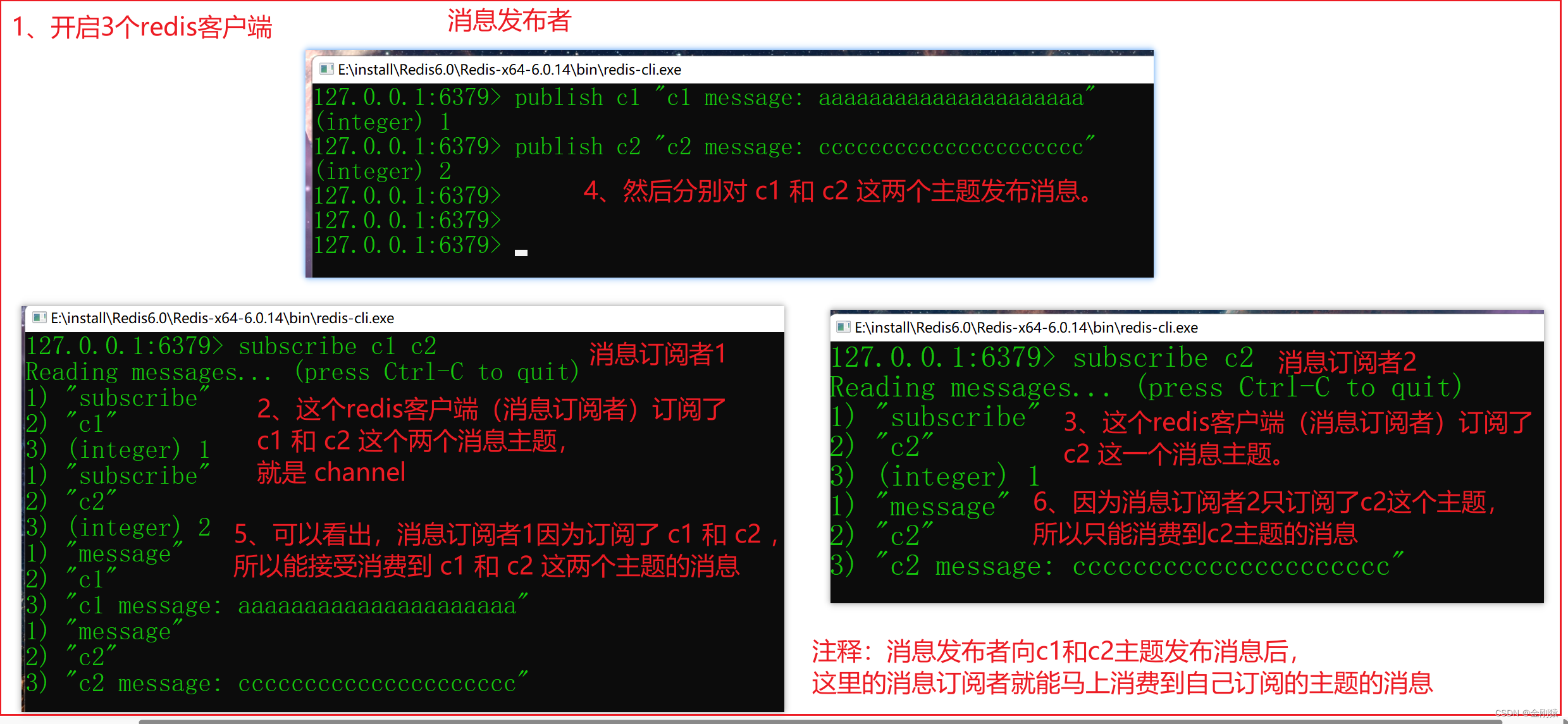
91、Redis - 事务 与 订阅-发布 相关的命令 及 演示
★ 事务相关的命令 Redis事务保证事务内的多条命令会按顺序作为整体执行,其他客户端发出的请求绝不可能被插入到事务处理的中间, 这样可以保证事务内所有命令作为一个隔离操作被执行。 Redis事务同样具有原子性,事务内所有命令要么全部被执…...
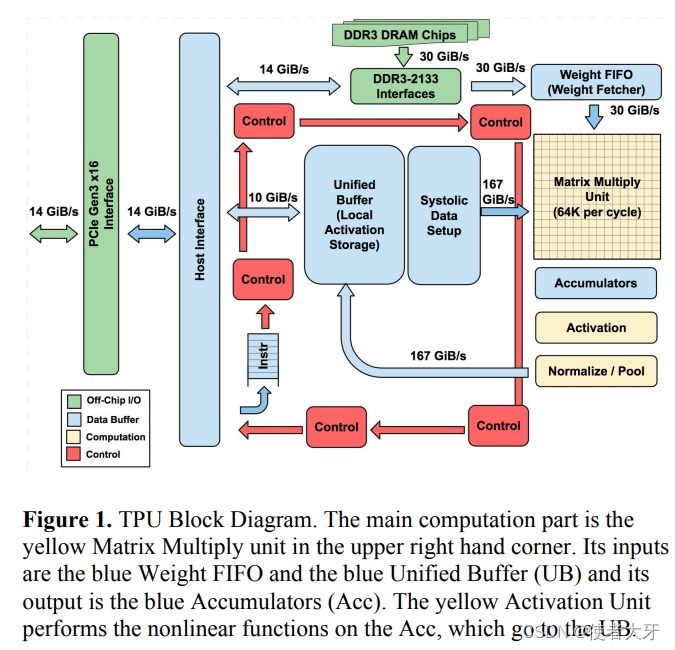
GPU如何成为AI的加速器
0. 前言 按照国际惯例,首先声明:本文只是我自己学习的理解,虽然参考了他人的宝贵见解,但是内容可能存在不准确的地方。如果发现文中错误,希望批评指正,共同进步。 本文关键词:GPU、深度学习、GP…...

Map声明、元素访问及遍历、⼯⼚模式、实现 Set - GO语言从入门到实战
Map声明、元素访问及遍历 - GO语言从入门到实战 Map 声明的方式 m := map[string]int{"one": 1, "two": 2, "three": 3} //m初始化时就已经设置了3个键值对,所以它的初始长度len(m)是3。m1 := map[string]int{} //m1被初始化为一个空的m…...
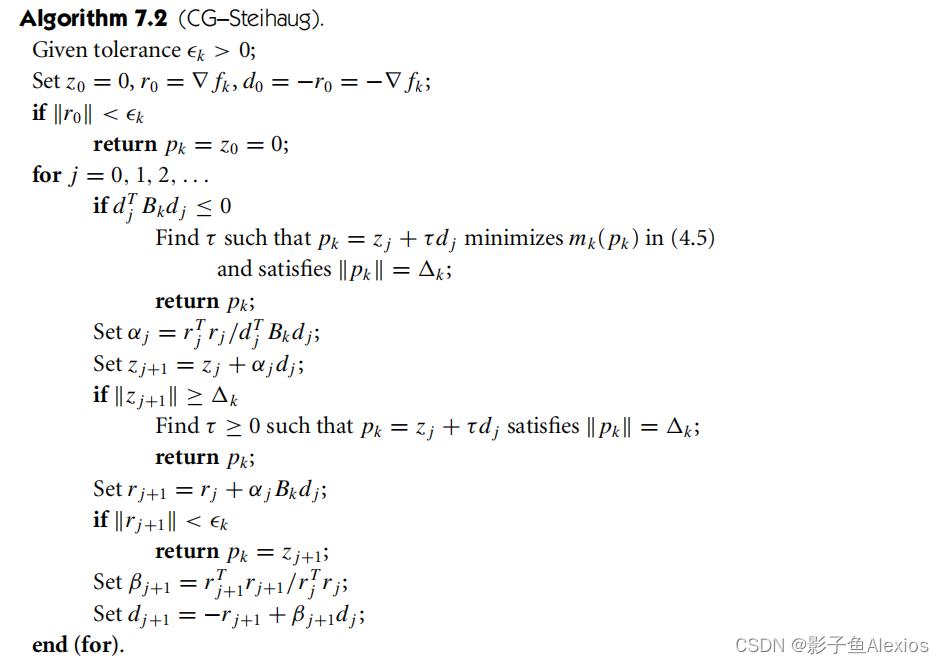
机器人中的数值优化|【七】线性搜索牛顿共轭梯度法、可信域牛顿共轭梯度法
机器人中的数值优化|【七】线性搜索牛顿共轭梯度法、可信域牛顿共轭梯度法 Line Search Newton-CG, Trust Region Newton-CG 往期回顾 机器人中的数值优化|【一】数值优化基础 机器人中的数值优化|【二】最速下降法,可行牛顿法的python实现,以Rosenbro…...

websocket实现go(server)与c#(client)通讯
go 服务端 使用到github.com/gorilla/websocket package mainimport ("fmt""github.com/gorilla/websocket""log""net/http" )func main() {var upgrader websocket.Upgrader{ReadBufferSize: 1024,WriteBufferSize: 1024,CheckOr…...

洛谷题目题解详细解答
洛谷是一个很不错的刷题软件,可是找不到合适的题解是个大麻烦,大家有啥可以私信问我,以下是我已经通过的题目。 你如果有哪一题不会(最好是我通过过的,我没过的也没关系),可以私信我࿰…...
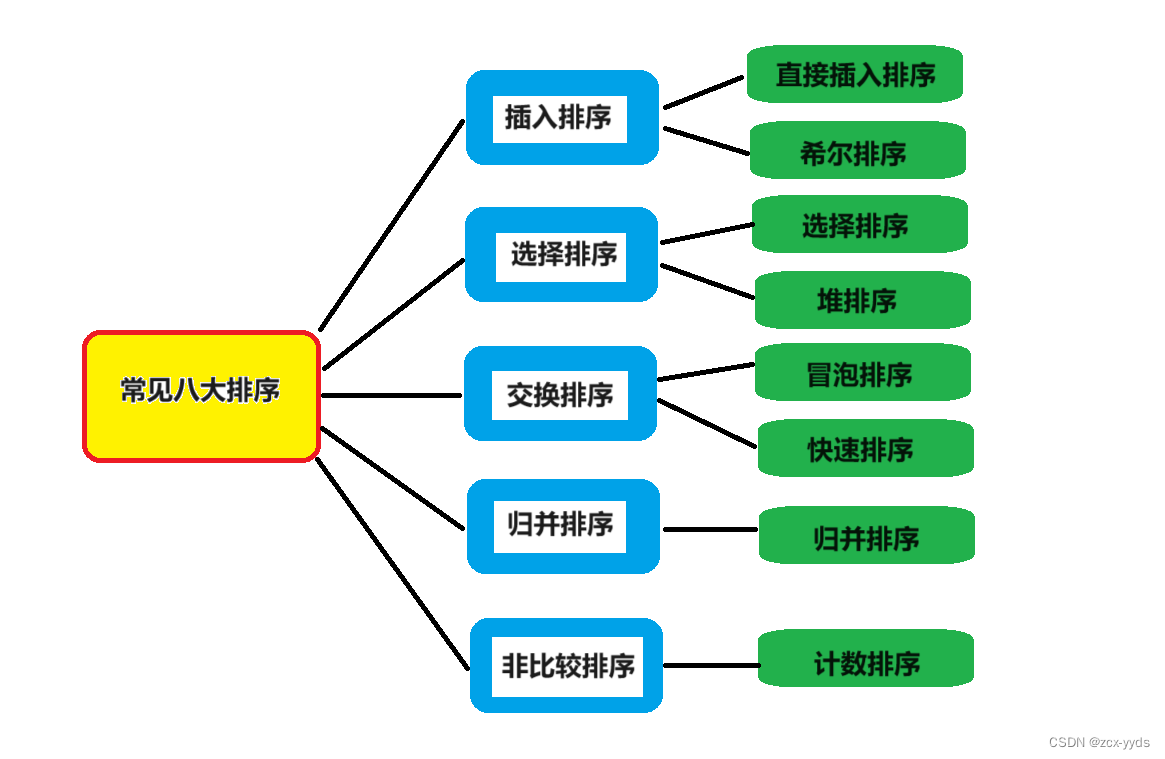
【C语言】八大排序算法
文章目录 一、冒泡排序1、定义2、思想及图解3、代码 二、快速排序1、hoare版本2、挖坑法3、前后指针法4、非递归快排5、快速排序优化1)三数取中选key值2)小区间优化 三、直接插入排序1、定义2、代码 四、希尔排序1、定义2、图解3、代码 五、选择排序1、排…...

2023年中国智能电视柜产量、需求量、市场规模及行业价格走势[图]
电视柜是随着电视机的发展和普及而演变出的家具种类,其主要作用是承载电视机,又称视听柜,随着生活水平的提高,与电视机相配套的电器设备也成为电视柜的收纳对象。 随着智能家具的发展,智能电视机柜的造型和风格都是有了…...

docker容器使用初体验
我们写程序时,都会搭建相关的环境,比如写了一个web,使用了tomcat、nginx等,现在想要把程序部署到云服务器或者在其他电脑上运行,就需要重新部署一遍环境,尤其是项目开源后,上手成本大。 docker…...

React Hooks ——性能优化Hooks
什么是Hooks Hooks从语法上来说是一些函数。这些函数可以用于在函数组件中引入状态管理和生命周期方法。 React Hooks的优点 简洁 从语法上来说,写的代码少了上手非常简单 基于函数式编程理念,只需要掌握一些JavaScript基础知识与生命周期相关的知识不…...
C#学习系列相关之多线程(一)----常用多线程方法总结
一、多线程的用途 在介绍多线程的方法之前首先应当知道什么是多线程, 在一个进程内部可以执行多个任务,而这每一个任务我们就可以看成是一个线程。是程序使用CPU的基本单位。进程是拥有资源的基本单位, 线程是CPU调度的基本单位。多线程的作用…...
Vscode爆红Delete `␍`eslintprettier/prettier
一、先看报错 文件中爆红,提示 Delete ␍eslintprettier/prettier 二、解决方案 项目根目录下,.prettierrc.js 文件中: endOfLine: auto,三、重启VsCode 此时不在爆红,问题完美解决...

Mac安装Ecplise产品报错:dose not contain the JNI_CreateJavaVM symbol
1. 絮絮叨叨 工作中需要借助Ecplise Memory Analyzer (MAT)分析dump文件,直接下载、安装、运行MAT报错 询问同事后,同事说可以先安装Ecplise,再以插件的形式安装MAT下载、安装好Eclipse,点击运行仍然报错,且错误信息一…...

如何使用大语言模型来绘制图画
请创作一张科技感十足的图片,包含siri和iphone两个元素,请帮我挑选合适的style和background 好的,我会为你创作一张科技感十足的图片,包含siri和iphone两个元素。我会根据你的要求,选择一种适合的风格和背景。请稍等一…...

代码随想录算法训练营第23期day11 | 20. 有效的括号、1047. 删除字符串中的所有相邻重复项 、150. 逆波兰表达式求值
目录 一、(leetcode 20)有效的括号 二、(leetcode 1047)删除字符串中的所有相邻重复项 用栈存放 将字符串直接当成栈 三、(leetcode 150)逆波兰表达式求值 一、(leetcode 20)…...
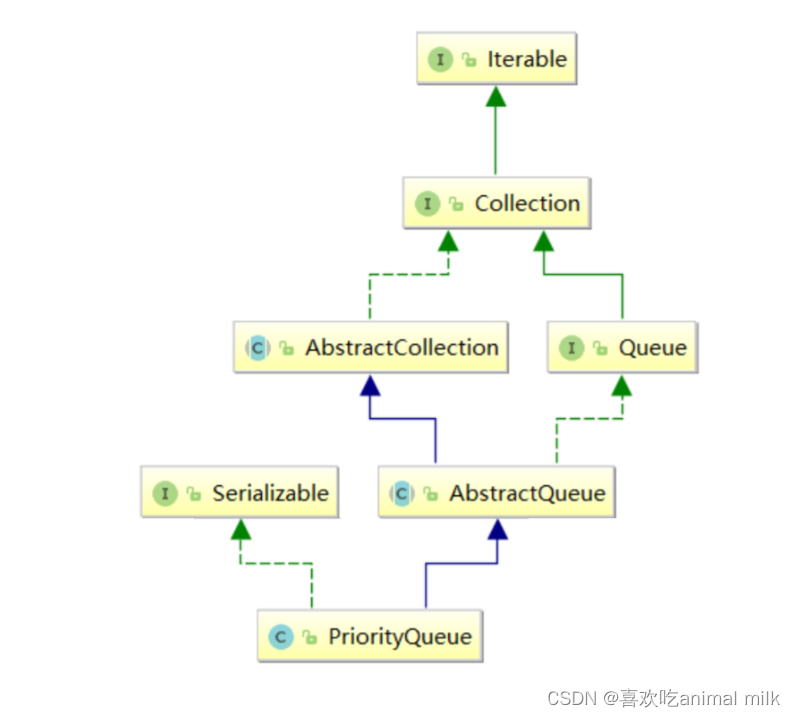
数据结构-优先级队列(堆)
文章目录 目录 文章目录 前言 一 . 堆 二 . 堆的创建(以大根堆为例) 堆的向下调整(重难点) 堆的创建 堆的删除 向上调整 堆的插入 三 . 优先级队列 总结 前言 大家好,今天给大家讲解一下堆这个数据结构和它的实现 - 优先级队列 一 . 堆 堆(Heap࿰…...
C++11新特性(语法糖,新容器)
距离C11版本发布已经过去那么多年了,为什么还称为新特性呢?因为笔者前面探讨的内容,除了auto,范围for这些常用的,基本上是用着C98的内容,虽说C11已经发布很多年,却是目前被使用最广泛的版本。因…...
开机可用内存分析Tip
一、开机内存简介 开机内存指的是开机一段时间稳定后的可用内存。一般项目都会挑选同平台其他优秀竞品内存数据,这个也是衡量性能的一个重要标准。所以要进行开机内存检测,同时优化非法内存进程占用。 二、测试前期核查任务 开机内存测试前要进行测试机…...

【Python基础】4. 基本语句
文章目录 注释(Comment)解释伴随行文本编码问题 输入输出语句(Input & Output)输出语句普通输出格式化输出(3种)format 格式总结 输入语句 基本语句if 语句match 语句(Python3.10 新增&…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

蓝桥杯 2024 15届国赛 A组 儿童节快乐
P10576 [蓝桥杯 2024 国 A] 儿童节快乐 题目描述 五彩斑斓的气球在蓝天下悠然飘荡,轻快的音乐在耳边持续回荡,小朋友们手牵着手一同畅快欢笑。在这样一片安乐祥和的氛围下,六一来了。 今天是六一儿童节,小蓝老师为了让大家在节…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

4. TypeScript 类型推断与类型组合
一、类型推断 (一) 什么是类型推断 TypeScript 的类型推断会根据变量、函数返回值、对象和数组的赋值和使用方式,自动确定它们的类型。 这一特性减少了显式类型注解的需要,在保持类型安全的同时简化了代码。通过分析上下文和初始值,TypeSc…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...
