蓝桥杯每日一题2023.10.5
3420. 括号序列 - AcWing题库
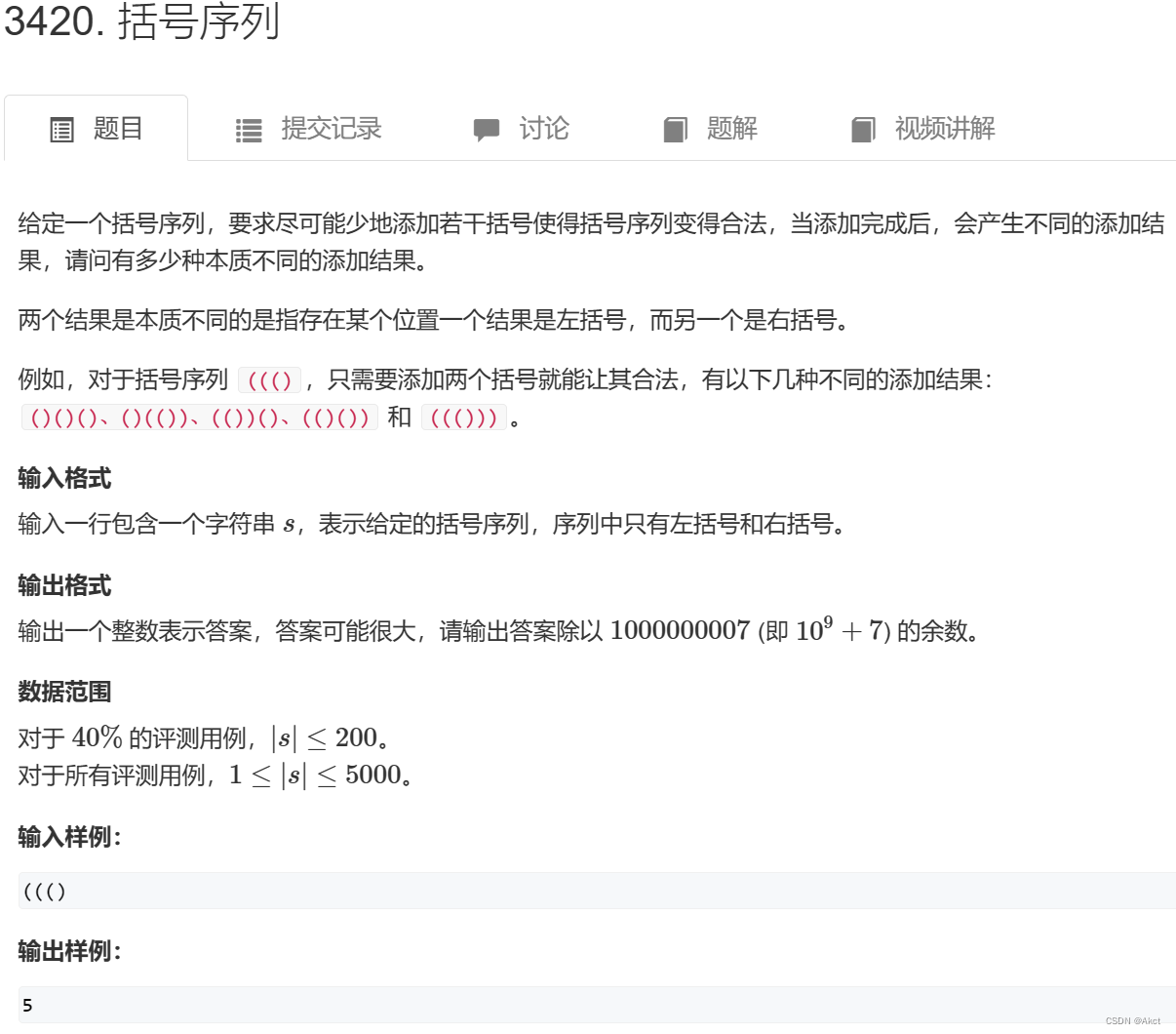
题目描述
题目分析
对于这一我们需要有前缀知识完全背包
完全背包的朴素写法:
#include<bits/stdc++.h>
using namespace std;
const int N = 1010;
int n, m, v[N], w[N], f[N][N];
int main()
{cin >> n >> m;for(int i = 1; i <= n; i ++)cin >> v[i] >> w[i];for(int i = 1; i <= n; i ++){for(int j = 0; j <= m; j ++){for(int k = 0; k * v[i] <= j; k ++){f[i][j] = max(f[i][j], f[i - 1][j - v[i] * k] + w[i] * k);}}}cout << f[n][m] << '\n';return 0;
}经行优化:
f[i][j] = f[i - 1][j - v[i] * k] + w[i] * k
f[i][j] = max(f[i - 1][j], f[i - 1][j - v] + w, f[i - 1][j - 2v] + 2w, f[i - 1][j - 3v] + 3w, ...)
f[i][j - v] = max( f[i - 1][j - v], f[i - 1][j - 2v] + w, f[i - 1][j - 3v] + 2w, ...)
f[i][j] = max(f[i - 1][j], f[i][j - v] + w)
#include<bits/stdc++.h>
using namespace std;
const int N = 1010;
int n, m, v[N], w[N], f[N][N];
int main()
{cin >> n >> m;for(int i = 1; i <= n; i ++)cin >> v[i] >> w[i];for(int i = 1; i <= n; i ++){for(int j = 0; j <= m; j ++){for(int k = 0; k * v[i] <= j; k ++){f[i][j] = f[i - 1][j];if(j >= v[i])f[i][j] = max(f[i][j], f[i][j - v[i]] + w[i]);}}}cout << f[n][m] << '\n';return 0;
}
首先由题意知我们左右括号的数量必须相等,对于任意前缀的左括号的数量必须大于等于有括号的数量(如果小于则此处必定需要添加括号)
我们可以分为两种方案使其独立存在,一种是只添加左括号,一种是只添加右括号,这两种方案各进行一次,将方案数相乘则为总方案数,对于左右进行的操作只需用同一代码即可,我们可以只写对左括号进行操作,对于右括号操作我们只需要将字符串翻转即可实现操作
使用动态规划来记录方案数
f[i][j] :只考虑前i部分,左括号比右括号多j 个的所有方案的集合(不同数量的左括号的方案数)
1.若s[i] == '(' f[i][j] = f[i - 1][j - 1](考虑前i - 1部分时,左括号数量比右括号数量多j - 1个,那么第i部分左括号就比右括号多j个)
2.若s[i] == ')' f[i][j] = f[i - 1][j + 1] + f[i - 1][j] + ... + f[i - 1][0](考虑前i - 1部分左括号数量最多比右括号数量多j + 1个,才能在第i部分通过添加或者不加左括号使左括号的数量比右括号的数量多j个)注:这里类似于完全背包的优化:f[i][j] = f[i - 1][j + 1] + f[i][j - 1],考虑越界问题,f[i][0]特判(j == 0,j - 1 = -1越界)f[i][0]可以考虑前i - 1部分左括号数和右括号数相等 和 左括号数比右括号数多一个的和
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 5010, mod = 1e9 + 7;
char s[N];
int n;
ll f[N][N];
ll work()
{memset(f, 0, sizeof f);f[0][0] = 1;for(int i = 1; i <= n; i ++){if(s[i] == '('){for(int j = 1; j <= n; j ++)f[i][j] = f[i - 1][j - 1];}else{f[i][0] = (f[i - 1][0] + f[i - 1][1]) % mod;for(int j = 1; j <= n; j ++)f[i][j] = (f[i - 1][j + 1] + f[i][j - 1]) % mod;}}for(int i = 0; i <= n; i ++){if(f[n][i])return f[n][i];}return -1;
}
int main()
{cin >> s + 1;n = strlen(s + 1);ll l = work();reverse(s + 1, s + n + 1);for(int i = 1; i <= n; i ++){if(s[i] == '(')s[i] = ')';else s[i] = '(';}ll r = work();cout << l * r % mod;return 0;
}相关文章:

蓝桥杯每日一题2023.10.5
3420. 括号序列 - AcWing题库 题目描述 题目分析 对于这一我们需要有前缀知识完全背包 完全背包的朴素写法: #include<bits/stdc.h> using namespace std; const int N 1010; int n, m, v[N], w[N], f[N][N]; int main() {cin >> n >> m;fo…...

PyTorch实例:简单线性回归的训练和反向传播解析
文章目录 🥦引言🥦什么是反向传播?🥦反向传播的实现(代码)🥦反向传播在深度学习中的应用🥦链式求导法则🥦总结 🥦引言 在神经网络中,反向传播算法…...

Arcgis提取玉米种植地分布,并以此为掩膜提取遥感影像
Arcgis提取玉米种植地分布上,并以此为掩膜提取遥感影像 一、问题描述 因为之前反演是整个研究区,然而土地利用类型有很多类,只在农田或者植被上进行反演,需要去除水体、建筑等其他类型,如何处理得到下图中只有耕地类…...

软件工程与计算总结(四)项目管理基础
目录 一.项目和项目管理 二.团队组织与管理 三.软件质量保障 四.软件配置管理 五.项目实践 一.项目和项目管理 1.软件开发远不是纯粹的编程,随着软件规模的增长,软件开发活动也变得越来越复杂~ 2.软件项目就是要将所有的软件开发活动组织起来&#…...
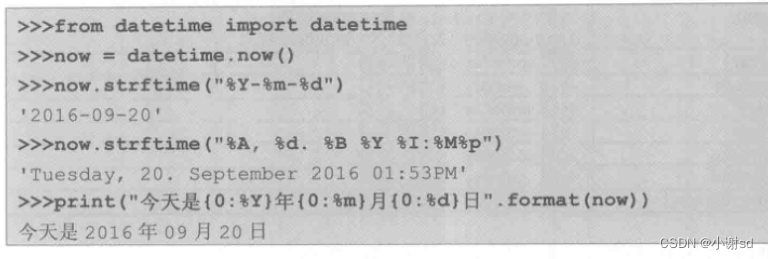
【Python】datetime 库
# timedelta(days, seconds, microseconds,milliseconds, minutes, hours, weeks) 默认按顺序传递参数 # 主要介绍 datetime.datetime 类 # 引入 from datetime import datetime today datetime.now() # 获取当前时间 2023-10-05 15:58:03.218651 today1 datetime.utcnow() #…...

从0开始python学习-28.selenium 需要图片验证的登录
url https://test.com/login driver.get(url) # 获取登录页面需要输入账号密码进行模拟登录操作 user driver.find_element(By.XPATH,//*[id"login"]/div[2]/div/form[2]/div[2]/div/div/input).send_keys(username) pwd driver.find_element(By.XPATH,//*[id&qu…...

Nginx搭建Rtmp流媒体服务,并使用Ffmpeg推流
文章目录 1.rtmp流媒体服务框架图2.nginx配置3.配置nginx4.使用ffmpeg推流5.实时推摄像头流 本项目在开发板上使用nginx搭建流媒体服务,利用ffmpeg进行推流,在pc上使用vlc media进行拉流播放。 1.rtmp流媒体服务框架图 2.nginx配置 下载:wge…...

IDEA 将一个普通Java工程转化为maven工程
打开IntelliJ IDEA并打开Java工程。 在项目窗口中,右键单击项目名称,选择“Add Framework Support”。 在弹出的窗口中,选择“Maven”。 在“Maven Information”窗口中,填写Group Id、Artifact Id和Version等基本信息。 点击…...
linux下的永久保存行号
linux下的永久保存行号 1.首先 这里是引用 输入命令:vi ~/.vimrc 其次 这里是引用 输入命令 set number...

92岁高龄的创始人张忠谋谈台积电发展史
一、张忠谋和台积电 在台北一间办公室里,张忠谋最近拿出一本印有彩色图案的旧书。它的标题是《VLSI 系统导论》,这是一本研究生水平的教科书,描述了计算机芯片设计的复杂性。92岁的张先生满怀敬意地举起它。 92岁高龄的台积电创始人张忠谋 “…...

【VIM】VIm初步使用
玩转Vim-从放弃到入门_哔哩哔哩_bilibili...
教育类《中学政史地》收稿方向-投稿邮箱
教育类《中学政史地》收稿方向-投稿邮箱 《中学政史地》收稿方向:中学政治、历史、地理类稿件 《中学政史地》创办于1987年,是我国唯一一份集中学政治、历史、地理三门学科为一体的综合性月刊。每月两期,分初中版和高中版。以服务学生、服务…...
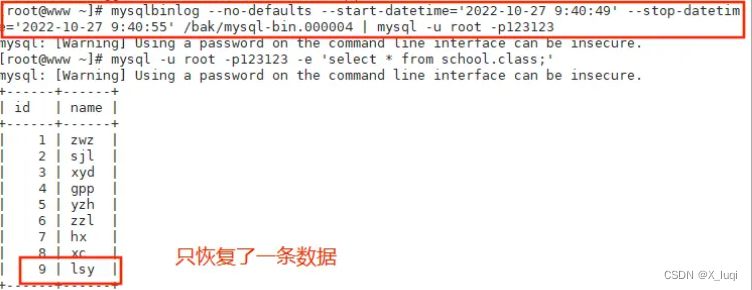
数据库的备份与恢复
数据备份的重要性 备份的主要目的是灾难恢复。 在生产环境中,数据的安全性至关重要。 任何数据的丢失都可能产生严重的后果。 造成数据丢失的原因: 程序错误人为操作错误运算错误磁盘故障灾难(如火灾、地震)和盗窃 数据库备份…...
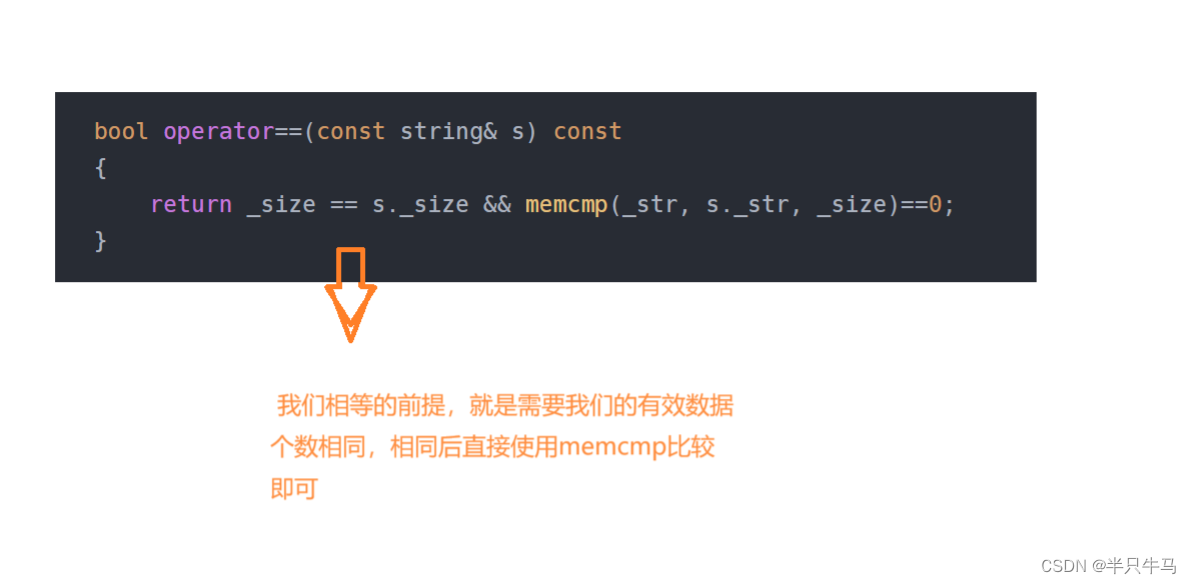
string类的模拟实现(万字讲解超详细)
目录 前言 1.命名空间的使用 2.string的成员变量 3.构造函数 4.析构函数 5.拷贝构造 5.1 swap交换函数的实现 6.赋值运算符重载 7.迭代器部分 8.数据容量控制 8.1 size和capacity 8.2 empty 9.数据修改部分 9.1 push_back 9.2 append添加字符串 9.3 运算符重载…...

C 函数指针
就像指针可以指向一般变量、数组、结构体那样,指针也可以指向函数。 函数指针的主要用途是向其他函数传递“回调”,或者模拟类和对象。 形式如下: int (*POINTER_NAME)(int a, int b) 这类似于指向数组的指针可以表示所指向的数组。指向函数…...

zkVM设计性能分析
1. 引言 本文主要参考: 2023年9月ZKSummit10 Wei Dai 1k(x) & Terry Chung 1k(x)分享视频 ZK10: Analysis of zkVM Designs - Wei Dai & Terry Chung 当前有各种zkVM,其设计思想各有不同,且各有取舍,本文重点对现有各z…...
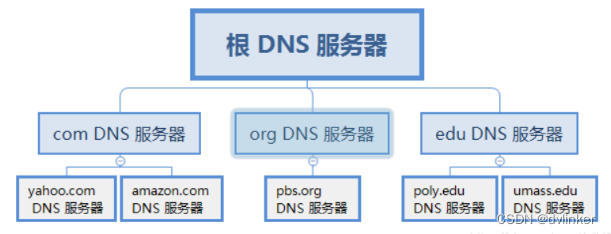
调用gethostbyname实现域名解析(附源码)
VC常用功能开发汇总(专栏文章列表,欢迎订阅,持续更新...)https://blog.csdn.net/chenlycly/article/details/124272585C软件异常排查从入门到精通系列教程(专栏文章列表,欢迎订阅,持续更新...&a…...

面向无线传感器网络WSN的增强型MODLEACH设计与仿真(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...
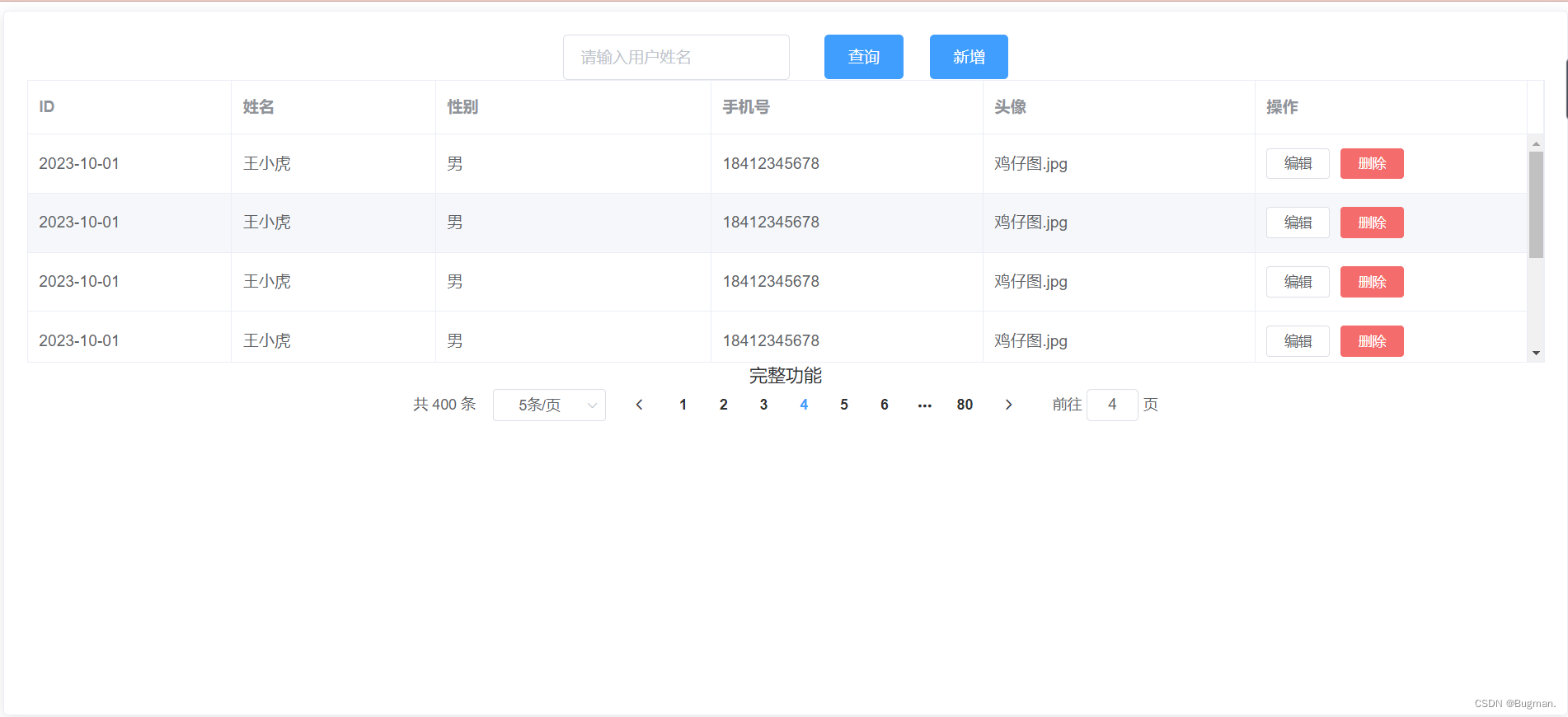
前端页面初步开发
<template><div><el-card class"box-card" style"height: 620px"><el-input v-model"query.name" style"width:200px" placeholder"请输入用户姓名"></el-input>   …...

【赠书活动第3期】《构建新型网络形态下的网络空间安全体系》——用“价值”的视角来看安全
目录 一、内容简介二、读者受众三、图书目录四、编辑推荐五、获奖名单 一、内容简介 经过30多年的发展,安全已经深入到信息化的方方面面,形成了一个庞大的产业和复杂的理论、技术和产品体系。 因此,需要站在网络空间的高度看待安全与网络的…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

三分算法与DeepSeek辅助证明是单峰函数
前置 单峰函数有唯一的最大值,最大值左侧的数值严格单调递增,最大值右侧的数值严格单调递减。 单谷函数有唯一的最小值,最小值左侧的数值严格单调递减,最小值右侧的数值严格单调递增。 三分的本质 三分和二分一样都是通过不断缩…...

【Linux手册】探秘系统世界:从用户交互到硬件底层的全链路工作之旅
目录 前言 操作系统与驱动程序 是什么,为什么 怎么做 system call 用户操作接口 总结 前言 日常生活中,我们在使用电子设备时,我们所输入执行的每一条指令最终大多都会作用到硬件上,比如下载一款软件最终会下载到硬盘上&am…...

Ubuntu系统多网卡多相机IP设置方法
目录 1、硬件情况 2、如何设置网卡和相机IP 2.1 万兆网卡连接交换机,交换机再连相机 2.1.1 网卡设置 2.1.2 相机设置 2.3 万兆网卡直连相机 1、硬件情况 2个网卡n个相机 电脑系统信息,系统版本:Ubuntu22.04.5 LTS;内核版本…...

文件上传漏洞防御全攻略
要全面防范文件上传漏洞,需构建多层防御体系,结合技术验证、存储隔离与权限控制: 🔒 一、基础防护层 前端校验(仅辅助) 通过JavaScript限制文件后缀名(白名单)和大小,提…...
