AtCoder Beginner Contest 232(A-G)
A - QQ solver (atcoder.jp)直接按题意模拟即可。
B - Caesar Cipher (atcoder.jp)按题意模拟即可
C - Graph Isomorphism (atcoder.jp)按题意模拟即可
D - Weak Takahashi (atcoder.jp) 一个非常套路的网格dp
E - Rook Path (atcoder.jp)
(1)题意
有一个H*W的网格,网格中有一个车初始在(x1,y1)这个位置,高桥操作K次后达到(x2,y2)的方案数是多少,每一次移动可以挪到一行或者这一列的任意一个位置上去,但是不能在原始位置。
(2)思路
考虑K不大,我们进行O(K)的dp。
定义dp[i][0]表示前i步操作操作完后和最终位置行列都不同的方案数
定义dp[i][1]表示前i步操作操作完后和最终位置列相同的方案数
定义dp[i][2]表示前i步操作操作完后和最终位置列相同的方案数
定义dp[i][3]表示前i步操作操作完后和最终位置行列都相同的方案数
1.首先若第i步操作想要变成行列都相同,则前(i - 1)步一定是行相同或者列相同
2.若第i步操作只要变成行相同,那么前面可能是通过行相同,但第i步走到了不同列,或者是前面i-1步行列都不同走到这行上来了,或者是前面行列都一样,走到不同的列去了。
3.若第i步操作只要变成列相同,那么前面可能是通过列相同,但第i步走到了不同行,或者是前面i-1步行列都不同走到这列上来了,或者是前面行列都一样,走到不同的行去了。
4.若第i步操作想要变成行列都不同,那么可能是通过行相同,然后走到了不同行,或者是列相同走到了不同列,或者是行列都不同又走到了行列都不同。
(3)代码
#include <bits/stdc++.h>
#define rep(i,z,n) for(int i = z;i <= n; i++)
#define per(i,n,z) for(int i = n;i >= z; i--)
#define PII pair<int,int>
#define fi first
#define se second
#define vi vector<int>
#define vl vector<ll>
#define pb push_back
#define sz(x) (int)x.size()
#define all(x) (x).begin(),(x).end()
using namespace std;
using ll = long long;
const int N = 1e6 + 10;
ll dp[N][4];
const ll mod = 998244353;
void solve()
{ll h,w,k;cin >> h >> w >> k;int x1,y1,x2,y2;cin >> x1 >> y1 >> x2 >> y2;if(x1 == x2 && y1 == y2) dp[0][3] = 1;else if(x1 == x2) dp[0][2] = 1;else if(y1 == y2) dp[0][1] = 1;else dp[0][0] = 1;//3 :行列都相同,2:行相同 1:列相同 0:行列都不同rep(i,1,k) {dp[i][3] = dp[i - 1][2] + dp[i - 1][1];dp[i][2] = dp[i - 1][2] * (w - 2) % mod + dp[i - 1][0] + dp[i - 1][3] * (w - 1) % mod;dp[i][1] = dp[i - 1][1] * (h - 2) % mod + dp[i - 1][0] + dp[i - 1][3] * (h - 1) % mod;dp[i][0] = dp[i - 1][2] * (h - 1) % mod + dp[i - 1][1] * (w - 1) + dp[i - 1][0] * (w - 2) % mod + dp[i - 1][0] * (h - 2) % mod;rep(j,0,3) dp[i][j] %= mod;}cout << dp[k][3];
}
int main()
{ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);int T = 1;// cin >> T;while(T --) solve();return 0;
}F - Simple Operations on Sequence (atcoder.jp)
(1)题意
给你一个长度为N的A序列和一个长度为N的B序列,你每次可以对A的一个元素进行加1或减1,这个操作一次花费X元,你也可以对A的一个元素i进行交换,交换A[i]和A[i + 1],这个操作花费Y元,问你使得A序列变成B序列的最小花费是多少?
(2)思路
考虑N不大,我们直接进行状压dp,dp[i]表示i这个点集我已经匹配了多少个A序列的位置,匹配了B的哪些位置需要的最小花费。
那么考虑转移首先枚举我要放的位置(也就是A未匹配的位置),我们把A[j]这个元素放到z这个位置上去,考虑前面已经放了met个,那么你一定需要交换met次。
最终输出dp[(1 << N) - 1]即可。
(3)代码
#include <bits/stdc++.h>
#define rep(i,z,n) for(int i = z;i <= n; i++)
#define per(i,n,z) for(int i = n;i >= z; i--)
#define PII pair<int,int>
#define fi first
#define se second
#define vi vector<int>
#define vl vector<ll>
#define pb push_back
#define sz(x) (int)x.size()
#define all(x) (x).begin(),(x).end()
using namespace std;
using ll = long long;
const int N = 20;
ll dp[1 << N];
int a[N],b[N];
void solve()
{ll n,X,Y;cin >> n >> X >> Y;rep(i,0,n - 1) cin >> a[i];rep(i,0,n - 1) cin >> b[i];memset(dp,0x3f,sizeof(dp));dp[0] = 0;for(int i = 0;i < (1 << n);i ++) {int z = __builtin_popcount(i),met = 0;for(int j = n - 1;j >= 0;j --) {if(!(i >> j & 1)) {dp[i | (1 << j)] = min(dp[i | 1 << j],dp[i] + 1ll * abs(a[j] - b[z]) * X + 1ll * met * Y);}else met ++;}}cout << dp[(1 << n) - 1];
}
int main()
{ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);int T = 1;// cin >> T;while(T --) solve();return 0;
}G - Modulo Shortest Path (atcoder.jp)
(1)题意
给你两个序列A和B,你有一条从i->j的权值为(A[i] + B[j]) % M的边,问你从1走到N的最短路径是多长。
(2)思路
考虑暴力,我们建边都要N^2,显然不可行,考虑优化建边。
对于A序列我们把i向M - A[i]连一条权值为0的边,对于B序列我们把B[i]向i连一条权值为0的边,对于[0,M - 1]把0->1,1->2.....M - 2->M - 1连一条权值为1的边,这样图就变成了这样。
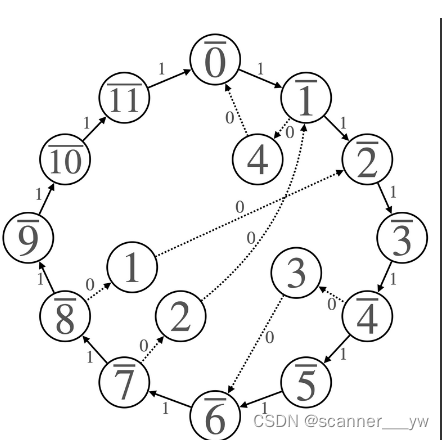
为什么要向M-A[i]连边而不是向A[i]连边呢?我们考虑分类讨论一下,画一下横坐标就行了。
好,现在我们的建边从N^2变成了2*N+M,显然M太大过不了,那么考虑其实有些边是用不到的,比如说0-1->2->3->4->5,难道我真要一步步跳过去?显然不可能,我们可以直接压缩成0->5。那哪些模数要用到呢,实际上就是我们建边用的M - a[i]和b[i],从小的向大的连一下即可,然后跑一个最短路就做完了。
(3)代码
#include <bits/stdc++.h>
#define rep(i,z,n) for(int i = z;i <= n; i++)
#define per(i,n,z) for(int i = n;i >= z; i--)
#define PII pair<int,int>
#define fi first
#define se second
#define vi vector<int>
#define vl vector<ll>
#define pb push_back
#define sz(x) (int)x.size()
#define all(x) (x).begin(),(x).end()
using namespace std;
using ll = long long;
const int N = 6e5 + 10;
vector<PII> e[N];
int a[N],b[N];
ll dis[N];
vector<int> ver;
int get(int x)
{return lower_bound(all(ver),x) - ver.begin() + 1;
}
inline ll dij(int s,int t)
{memset(dis,0x3f,sizeof(dis));dis[s] = 0;priority_queue<pair<ll,int>,vector<pair<ll,int>>,greater<pair<ll,int>>> q;q.push({dis[s],s});while(!q.empty()) {auto [val,u] = q.top();q.pop();for(auto [v,w]: e[u]) {if(dis[v] > val + w) {dis[v] = val + w;q.push({dis[v],v});}}}return dis[t];
}
void solve()
{int n,m;cin >> n >> m;rep(i,1,n) {cin >> a[i];a[i] = (m - a[i]) % m;ver.pb(a[i]);}rep(i,1,n) {cin >> b[i];ver.pb(b[i]);}sort(all(ver));rep(i,1,n) {a[i] = get(a[i]);b[i] = get(b[i]);e[i + sz(ver)].pb({a[i],0});e[b[i]].pb({i + sz(ver),0});}rep(i,1,sz(ver) - 1) {e[i].pb({i + 1,ver[i] - ver[i - 1]});}e[sz(ver)].pb({1,(ver[0] -ver[sz(ver) - 1] + m) % m});cout << dij(1 + sz(ver),n + sz(ver));
}
int main()
{ios::sync_with_stdio(false);cin.tie(0),cout.tie(0);int T = 1;// cin >> T;while(T --) solve();return 0;
}相关文章:

AtCoder Beginner Contest 232(A-G)
A - QQ solver (atcoder.jp)直接按题意模拟即可。 B - Caesar Cipher (atcoder.jp)按题意模拟即可 C - Graph Isomorphism (atcoder.jp)按题意模拟即可 D - Weak Takahashi (atcoder.jp) 一个非常套路的网格dp E - Rook Path (atcoder.jp) (1)题意 有…...
-第5章 运输层)
计算机网络(第8版)-第5章 运输层
5.1 运输层协议概述 5.1.1 进程之间的通信 图5-1 中两个运输层之间有一个深色双向粗箭头,写明“运输层提供应用进程间的逻辑通信”。 图5-1 运输层为相互通信的应用进程提供了逻辑通信 5.1.2 运输层的两个主要协议 5.1.3 运输层的端口 请注意,这种…...
AtCoder Beginner Contest 231(D-F,H)
D - Neighbors (atcoder.jp) (1)题意 给出M组关系,问是否有一个排列,能表示A[i]和B[i]相邻 (2)思路 考虑如果有环,显然不能满足排列,因为排列中度数最多为2,若有超过2的显…...

【Python】map
map()函数是Python内置函数之一,它的主要作用是将一个函数应用于可迭代对象中的每个元素,并返回一个包含结果的迭代器。 map()函数的语法如下: map(function, iterable)function参数是一个函数,表示要应用于可迭代对象每个元素的…...

Swift 5.9 与 SwiftUI 5.0 中新 Observation 框架应用之深入浅出
0. 概览 Swift 5.9 一声炮响为我们带来全新的宏(Macro)机制,也同时带来了干霄凌云的 Observation 框架。 Observation 框架可以增强通用场景下的使用,也可以搭配 SwiftUI 5.0 而获得双剑合璧的更强威力。 在本篇博文,…...

【已解决】在 Vite 项目中使用 eslint-config-ali 时遇到的解析错误
错误还原 搭建 Vite 项目 pnpm create vite my-vue-app --template vue-ts安装 eslint-config-ali pnpm i -D eslint-config-ali typescript-eslint/parser typescript-eslint/eslint-plugin eslint-plugin-import eslint-import-resolver-typescript vue-eslint-parser esl…...
蓝桥杯每日一题2023.10.5
3420. 括号序列 - AcWing题库 题目描述 题目分析 对于这一我们需要有前缀知识完全背包 完全背包的朴素写法: #include<bits/stdc.h> using namespace std; const int N 1010; int n, m, v[N], w[N], f[N][N]; int main() {cin >> n >> m;fo…...

PyTorch实例:简单线性回归的训练和反向传播解析
文章目录 🥦引言🥦什么是反向传播?🥦反向传播的实现(代码)🥦反向传播在深度学习中的应用🥦链式求导法则🥦总结 🥦引言 在神经网络中,反向传播算法…...

Arcgis提取玉米种植地分布,并以此为掩膜提取遥感影像
Arcgis提取玉米种植地分布上,并以此为掩膜提取遥感影像 一、问题描述 因为之前反演是整个研究区,然而土地利用类型有很多类,只在农田或者植被上进行反演,需要去除水体、建筑等其他类型,如何处理得到下图中只有耕地类…...

软件工程与计算总结(四)项目管理基础
目录 一.项目和项目管理 二.团队组织与管理 三.软件质量保障 四.软件配置管理 五.项目实践 一.项目和项目管理 1.软件开发远不是纯粹的编程,随着软件规模的增长,软件开发活动也变得越来越复杂~ 2.软件项目就是要将所有的软件开发活动组织起来&#…...
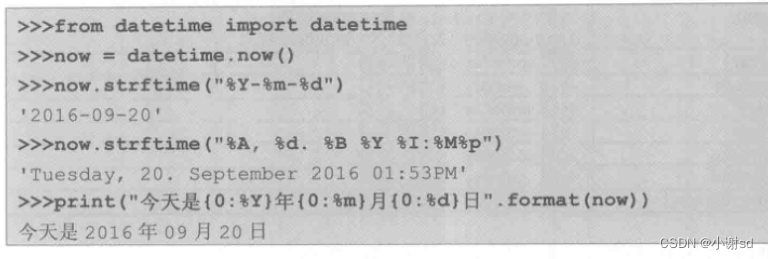
【Python】datetime 库
# timedelta(days, seconds, microseconds,milliseconds, minutes, hours, weeks) 默认按顺序传递参数 # 主要介绍 datetime.datetime 类 # 引入 from datetime import datetime today datetime.now() # 获取当前时间 2023-10-05 15:58:03.218651 today1 datetime.utcnow() #…...

从0开始python学习-28.selenium 需要图片验证的登录
url https://test.com/login driver.get(url) # 获取登录页面需要输入账号密码进行模拟登录操作 user driver.find_element(By.XPATH,//*[id"login"]/div[2]/div/form[2]/div[2]/div/div/input).send_keys(username) pwd driver.find_element(By.XPATH,//*[id&qu…...

Nginx搭建Rtmp流媒体服务,并使用Ffmpeg推流
文章目录 1.rtmp流媒体服务框架图2.nginx配置3.配置nginx4.使用ffmpeg推流5.实时推摄像头流 本项目在开发板上使用nginx搭建流媒体服务,利用ffmpeg进行推流,在pc上使用vlc media进行拉流播放。 1.rtmp流媒体服务框架图 2.nginx配置 下载:wge…...

IDEA 将一个普通Java工程转化为maven工程
打开IntelliJ IDEA并打开Java工程。 在项目窗口中,右键单击项目名称,选择“Add Framework Support”。 在弹出的窗口中,选择“Maven”。 在“Maven Information”窗口中,填写Group Id、Artifact Id和Version等基本信息。 点击…...
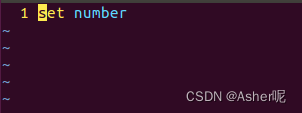
linux下的永久保存行号
linux下的永久保存行号 1.首先 这里是引用 输入命令:vi ~/.vimrc 其次 这里是引用 输入命令 set number...

92岁高龄的创始人张忠谋谈台积电发展史
一、张忠谋和台积电 在台北一间办公室里,张忠谋最近拿出一本印有彩色图案的旧书。它的标题是《VLSI 系统导论》,这是一本研究生水平的教科书,描述了计算机芯片设计的复杂性。92岁的张先生满怀敬意地举起它。 92岁高龄的台积电创始人张忠谋 “…...

【VIM】VIm初步使用
玩转Vim-从放弃到入门_哔哩哔哩_bilibili...
教育类《中学政史地》收稿方向-投稿邮箱
教育类《中学政史地》收稿方向-投稿邮箱 《中学政史地》收稿方向:中学政治、历史、地理类稿件 《中学政史地》创办于1987年,是我国唯一一份集中学政治、历史、地理三门学科为一体的综合性月刊。每月两期,分初中版和高中版。以服务学生、服务…...
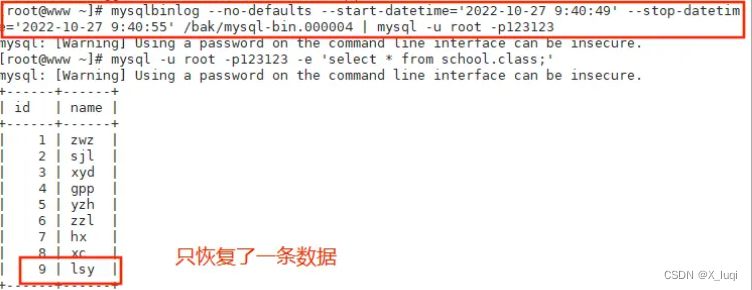
数据库的备份与恢复
数据备份的重要性 备份的主要目的是灾难恢复。 在生产环境中,数据的安全性至关重要。 任何数据的丢失都可能产生严重的后果。 造成数据丢失的原因: 程序错误人为操作错误运算错误磁盘故障灾难(如火灾、地震)和盗窃 数据库备份…...
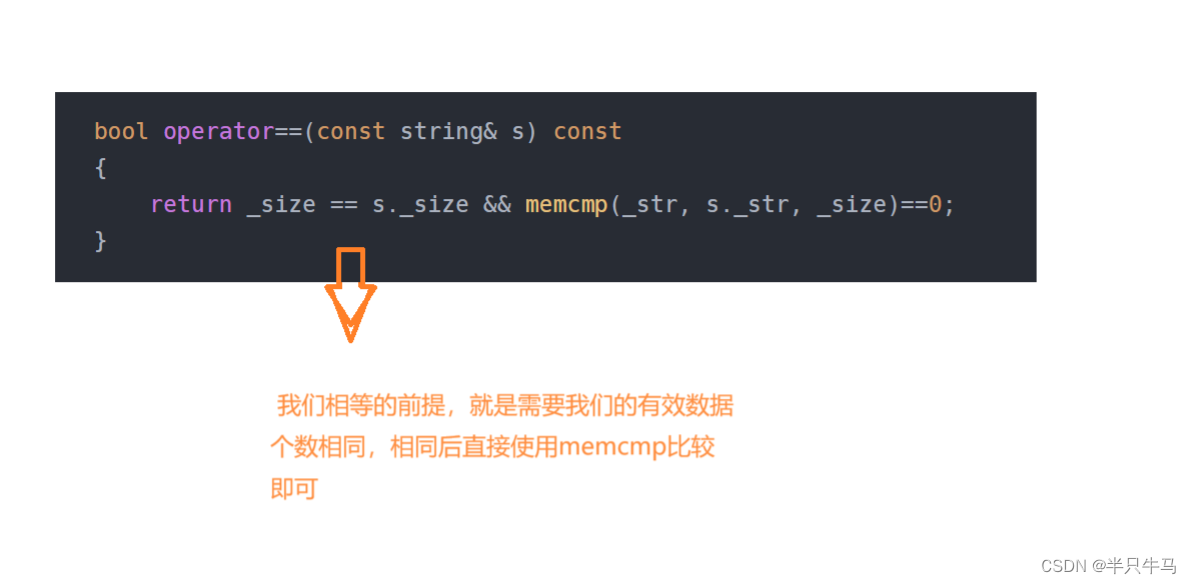
string类的模拟实现(万字讲解超详细)
目录 前言 1.命名空间的使用 2.string的成员变量 3.构造函数 4.析构函数 5.拷贝构造 5.1 swap交换函数的实现 6.赋值运算符重载 7.迭代器部分 8.数据容量控制 8.1 size和capacity 8.2 empty 9.数据修改部分 9.1 push_back 9.2 append添加字符串 9.3 运算符重载…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...

pikachu靶场通关笔记19 SQL注入02-字符型注入(GET)
目录 一、SQL注入 二、字符型SQL注入 三、字符型注入与数字型注入 四、源码分析 五、渗透实战 1、渗透准备 2、SQL注入探测 (1)输入单引号 (2)万能注入语句 3、获取回显列orderby 4、获取数据库名database 5、获取表名…...

MySQL的pymysql操作
本章是MySQL的最后一章,MySQL到此完结,下一站Hadoop!!! 这章很简单,完整代码在最后,详细讲解之前python课程里面也有,感兴趣的可以往前找一下 一、查询操作 我们需要打开pycharm …...
