【数据结构与算法】树、二叉树的概念及结构(详解)
前言:
💥🎈个人主页:Dream_Chaser~ 🎈💥
✨✨专栏:http://t.csdn.cn/oXkBa
⛳⛳本篇内容:c语言数据结构--树以及二叉树的概念与结构

目录
一.树概念及结构
1.树的概念
1.1树与非树
树的特点:
非树(图)的特点:
1.2 关于树的细致概念
1.3树的表示
1.4树在实际中的运用(表示文件系统的目录树结构)
二.二叉树概念及结构
1.概念
2.现实中的二叉树:
2.3特殊的二叉树:
2.4 二叉树的性质
证明性质2和1
习题练习
一.树概念及结构
1.树的概念
树是一种 非线性的数据结构,它是由n(n>=0)个有限结点组成一个具有层次关系的集合。 把它叫做树是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。

1.1树与非树

树的特点:
- 有一个特殊的结点,称为根结点,根节点没有前驱结点(没有父节点)
下面的两点一起理解:
- 除根节点外,其余结点被分成M(M>0)个互不相交的集合T1、T2、……、Tm,其中每一个集合Ti(1<= i <= m)又是一棵结构与树类似的子树。每棵子树的根结点有且只有一个前驱,可以有0个或多个后继
- 因此,树是递归定义的。
可以理解为:
由根节点指向了各子树,子树的双亲节点又可以作为根节点,指向它们的孩子节点
非树(图)的特点:


注意:树形结构中,子树之间不能有交集,否则就不是树形结构
3.一棵N个结点的树有N-1条边

1.2 关于树的细致概念
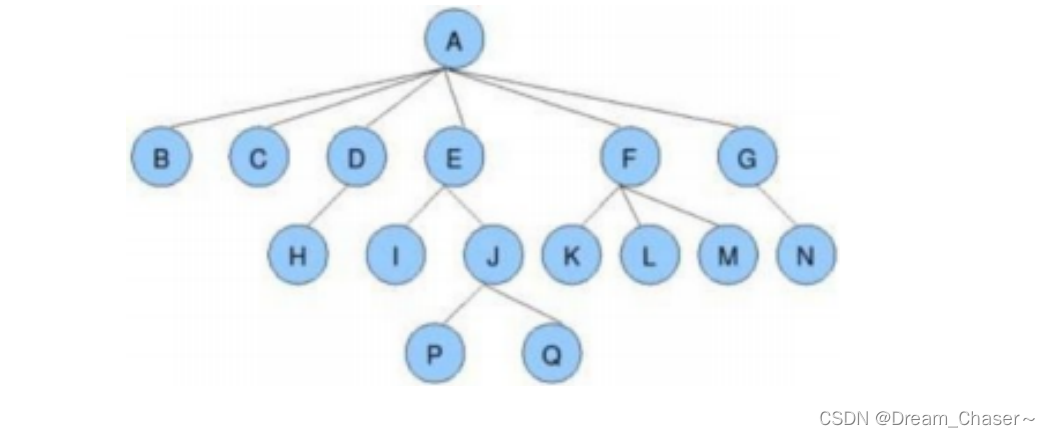
下面有个✅的是比较重要的知识点
✅节点的度:一个节点含有的子树的个数称为该节点的度; 如上图:A的为6
✅叶节点或终端节点:度为0的节点称为叶节点; 如上图:B、C、H、I...等节点为叶节点
✅非终端节点或分支节点:度不为0的节点; 如上图:D、E、F、G...等节点为分支节点
✅双亲节点或父节点:若一个节点含有子节点,则这个节点称为其子节点的父节点; 如上图:A是B的父节点
✅孩子节点或子节点:一个节点含有的子树的根节点称为该节点的子节点; 如上图:B是A的孩子节点
✅兄弟节点:具有相同父节点的节点互称为兄弟节点; 如上图:B、C是兄弟节点
树的度:一棵树中,最大的节点的度称为树的度; 如上图:树的度为6
节点的层次:从根开始定义起,根为第1层,根的子节点为第2层,以此类推;
✅树的高度或深度:树中节点的最大层次; 如上图:树的高度为4
堂兄弟节点:双亲在同一层的节点互为堂兄弟;如上图:H、I互为兄弟节点
✅节点的祖先:从根到该节点所经分支上的所有节点;如上图:A是所有节点的祖先
✅子孙:以某节点为根的子树中任一节点都称为该节点的子孙。如上图:所有节点都是A的子孙
森林:由m(m>0)棵互不相交的树的集合称为森林
对各知识点的进一步画图解析:
- 节点的度:与该节点直接相连的边的数量

- 叶节点(终端节点):度为0的节点
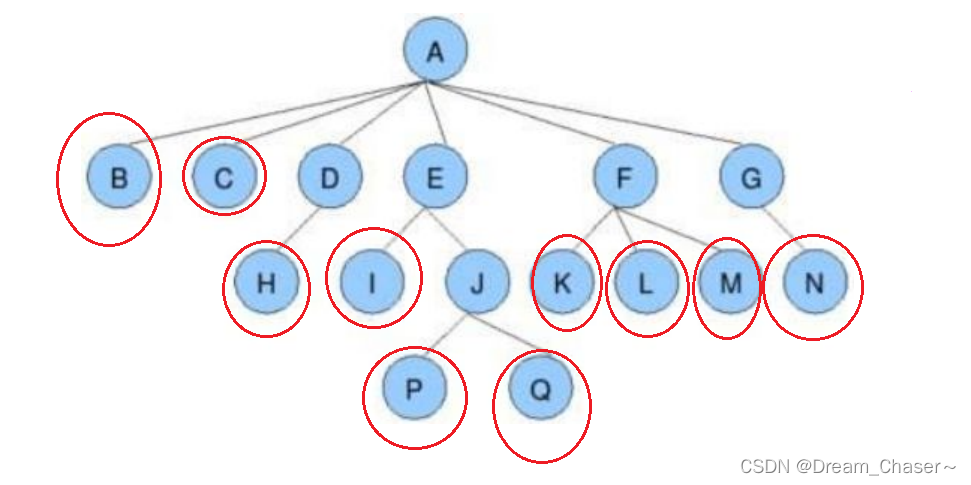
- 分支节点(非终端节点):度不为0的节点

- 父节点(双亲节点):一个节点的直接前驱就是它的父节点

- 子节点(孩子节点):一个节点的直接后继就是它的子节点

- 兄弟节点:由同一个父节点生出来的都是互为兄弟节点

- 树的度:一棵树中,最大的节点的度称为树的度
- 节点的层次:从上往下数,从根开始定义起,根为第1层,根的子节点为第2层,以此类推;(默认是从1开始)
- 树的高度(深度):树中节点的最大层次,下图的高度就是4

- 节点的高度:从下往上数
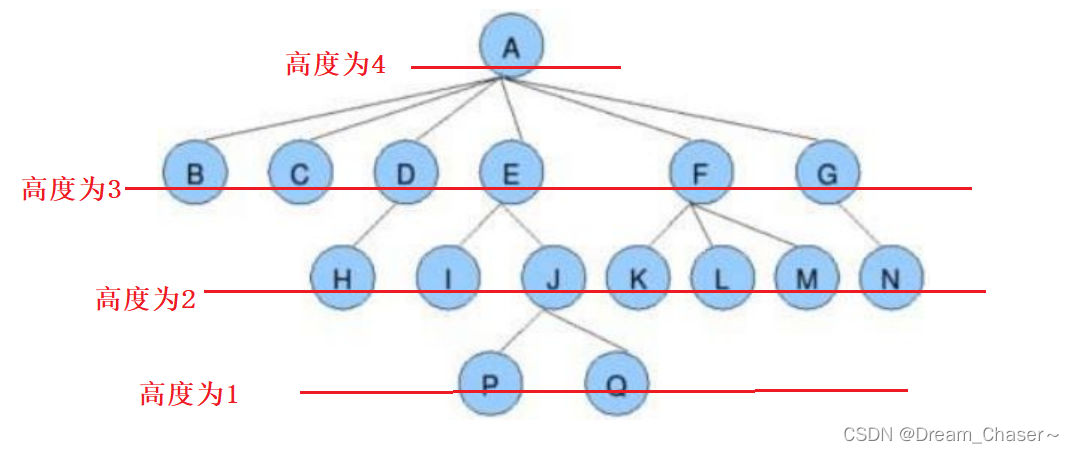
- 堂兄弟节点:双亲在同一层的节点互为堂兄弟
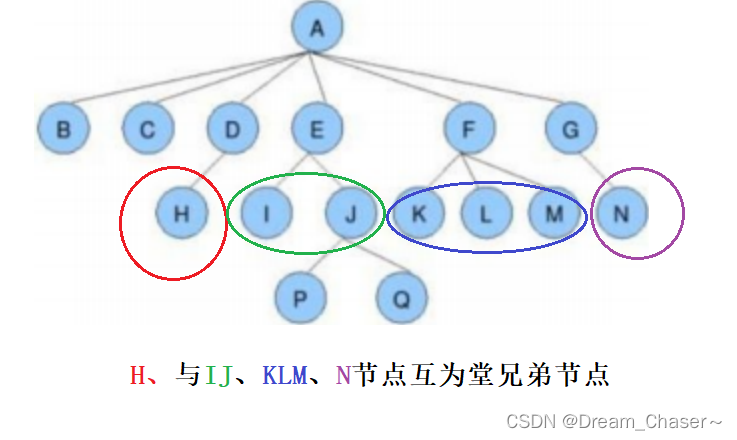
- 节点的祖先:指从该节点向上追溯到根节点的路径上的所有节点,包括该节点的父节点、父节点的父节点,以此类推,直到达到根节点为止。
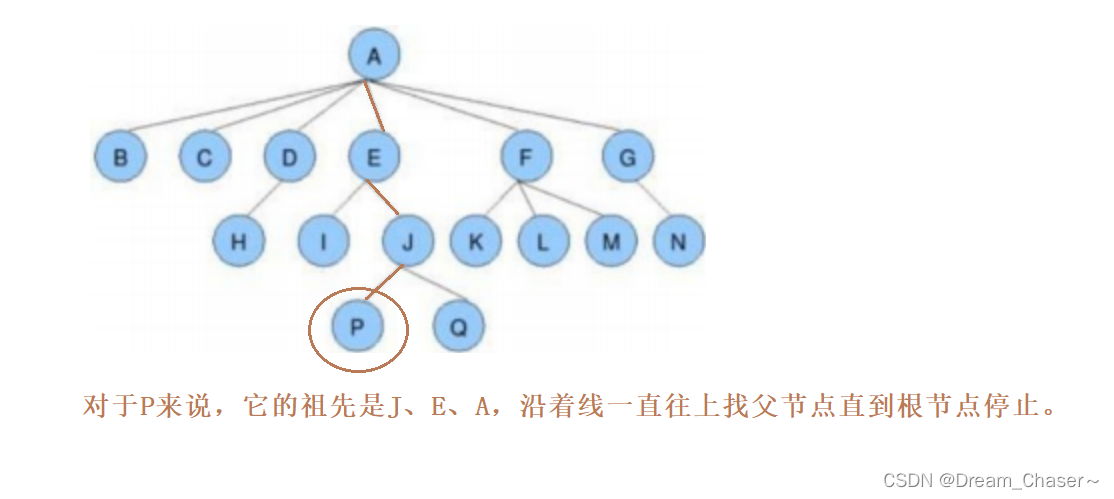
- 子孙:从该节点向下追溯到所有末端节点的路径上的所有节点,包括该节点的直接子节点、子节点的子节点,以此类推,直到达到叶子节点为止。

- 森林:是由多个不相交的树组成的集合(并查集)
1.3树的表示

B、顺序表存储孩子。

C、双亲表示法。(每个位置只存双亲的指针或者下标)

D、左孩子右兄弟表示法--简化树结构定义
树结构相对线性表就比较复杂了,要存储表示起来就比较麻烦了,既然保存值域,也要保存结点和结点之间的关系,实际中树有很多种表示方式如:双亲表示法,孩子表示法、孩子双亲表示法以及孩子兄弟表示法等。我们这里就简单的了解其中最常用的孩子兄弟表示法。
typedef int DataType;
struct Node
{struct Node* _firstChild1; // 第一个孩子结点struct Node* _pNextBrother; // 指向其下一个兄弟结点DataType _data; // 结点中的数据域
};画图解析:

1.4树在实际中的运用(表示文件系统的目录树结构)

二.二叉树概念及结构
1.概念
一棵二叉树是结点的一个有限集合,该集合:1. 或者为空2. 由一个根节点加上两棵别称为左子树和右子树的二叉树组成
 从上图可以看出:
从上图可以看出:
1. 二叉树不存在度大于2的结点(度为0也可以)2. 二叉树的子树有左右之分,次序不能颠倒,因此二叉树是有序树注意:对于任意的二叉树都是由以下几种情况复合而成的:
2.现实中的二叉树:

2.3特殊的二叉树:
1. 满二叉树:一个二叉树,如果每一个层的结点数都达到最大值,则这个二叉树就是满二叉树。也就是 说,如果一个二叉树的层数为K,且结点总数是2^k-1 ,则它就是满二叉树。2.完全二叉树:完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K的,有n个结点的二叉树,当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。

2.4 二叉树的性质
1. 若 i>0 , i 位置节点的双亲序号: (i-1)/2 ; i=0 , i 为根节点编号,无双亲节点2. 若 2i+1<n ,左孩子序号: 2i+1 , 2i+1>=n 否则无左孩子3. 若 2i+2<n ,右孩子序号: 2i+2 , 2i+2>=n 否则无右孩子
证明性质2和1

习题练习
1. 某二叉树共有 399 个结点,其中有 199 个度为 2 的结点,则该二叉树中的叶子结点数为( B)A 不存在这样的二叉树B 200C 198D 199解析: 2.下列数据结构中,不适合采用顺序存储结构的是( A)A 非完全二叉树B 堆C 队列D 栈解析:顺序存储结构适合于具有连续存储空间的数据结构,其中元素按照线性顺序存储。 对于非完全二叉树,由于其结构不规则,无法通过连续的存储空间来表示。因此,非完全二叉树不适合采用顺序存储结构。B. 堆、C. 队列、D. 栈都可以通过顺序存储结构有效地实现。堆是一种完全二叉树,可以使用数组来表示。队列和栈可以使用数组或者链表来表示,都适合顺序存储结构。3.在具有 2n 个结点的完全二叉树中,叶子结点个数为(A )A nB n+1C n-1D n/2
2.下列数据结构中,不适合采用顺序存储结构的是( A)A 非完全二叉树B 堆C 队列D 栈解析:顺序存储结构适合于具有连续存储空间的数据结构,其中元素按照线性顺序存储。 对于非完全二叉树,由于其结构不规则,无法通过连续的存储空间来表示。因此,非完全二叉树不适合采用顺序存储结构。B. 堆、C. 队列、D. 栈都可以通过顺序存储结构有效地实现。堆是一种完全二叉树,可以使用数组来表示。队列和栈可以使用数组或者链表来表示,都适合顺序存储结构。3.在具有 2n 个结点的完全二叉树中,叶子结点个数为(A )A nB n+1C n-1D n/2和节点个数相关的公式有二:
n0 = n2 + 1,N = n0 + n1 + n2
已知总个数N为2n,那么只要知道n1即可求出n0.
这里有一个重要的结论:
在完全二叉树中,如果节点总个数为奇数,则没有度为1的节点;如果节点总个数为偶数,只有一个度为1的节点。
节点个数是偶数,只有一个度为1的节点
节点个数是奇数,没有度为1的节点
2n为偶数,因此有一个度为1的节点。
2n = n0 + 1 + n2 = n0 + 1 + n0 - 1
2n = 2n0
n0 = n,故选A
4.一棵完全二叉树的节点数位为531个,那么这棵树的高度为( B)A 11B 10C 8D 12解析:根据性质4,h=log2(n+1),n=531,h = log2(532),找一个最接近的数就是log2(512),也就是log2(2^9),向上取整,n=10;5.一个具有767个节点的完全二叉树,其叶子节点个数为(B)A 383B 384C 385D 386解析:N=767个节点数是奇数个,所以N= n0+ n2(奇数个没有度为1的节点) ,由n0 = n2+1; N = 2n0 - 1 ,那么n0 = (N + 1) / 2 = 384
相关文章:

【数据结构与算法】树、二叉树的概念及结构(详解)
前言: 💥🎈个人主页:Dream_Chaser~ 🎈💥 ✨✨专栏:http://t.csdn.cn/oXkBa ⛳⛳本篇内容:c语言数据结构--树以及二叉树的概念与结构 目录 一.树概念及结构 1.树的概念 1.1树与非树 树的特点࿱…...
)
函数指针数组指针(指向函数指针数组的指针)
一、什么是函数指针数组指针? 本质是指针,指向函数指针数组,存放函数指针数组的地址。 代码如下: pfArr是函数指针数组 p是函数指针数组指针 int main() {int(*pfArr[])(int, int) { Add,Sub };//函数指针数组int(*(*p)[])(int, …...

经典算法-----汉诺塔问题
前言 今天我们学习一个老经典的问题-----汉诺塔问题,可能在学习编程之前我们就听说过这个问题,那这里我们如何去通过编程的方式去解决这么一个问题呢?下面接着看。 汉诺塔问题 问题描述 这里是引用汉诺塔问题源自印度一个古老的传说&#x…...
博客之站项目测试报告
项目背景项目功能测试计划Bug总结升级自动化测试正常登录流程 项目背景 1:博客之站系统是采用前后端分离的方式来实现;使用MySQL、Redis数据库储存相关数据;同时部署到云服务器上。 2:包含注册页、登录页、博客列表页、个人列表页…...

k8s晋级之管理容器的计算资源
概述 在 Kubernetes 中创建工作负载时,您可以为 Pod 中的每一个容器指定其所需要的内存(RAM)大小和 CPU 数量。如果这些信息被指定了,Kubernetes 调度器可以更好的决定将 Pod 调度到哪一个节点。对于容器来说,其所需要…...

计算机竞赛 深度学习火车票识别系统
文章目录 0 前言1 课题意义课题难点: 2 实现方法2.1 图像预处理2.2 字符分割2.3 字符识别部分实现代码 3 实现效果4 最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 图像识别 火车票识别系统 该项目较为新颖,适…...
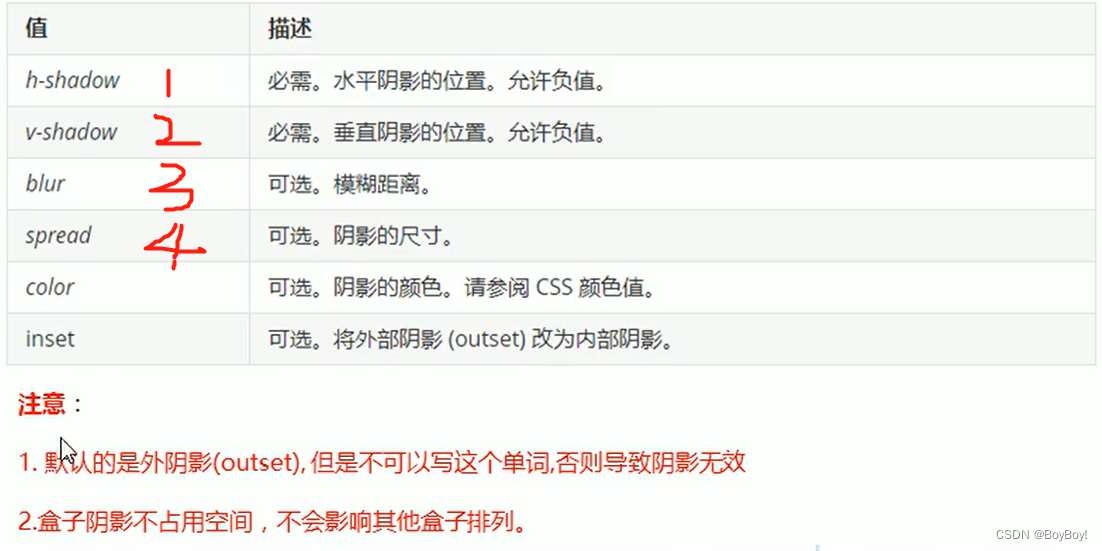
盒子阴影和网页布局
盒子阴影 box-shadow: 10px 10px 10px 4px rgba(0,0,0,.3);//最后一个是透明度 传统网页布局的三种方式 标准流 就是按照规定好的默认方式排列 1.块级元素:div、hr、p、h1~h2、ul、ol、dl、form、table 行内元素会按照书顺序,从左到右顺序排列&#…...

Ph.D,一个Permanent head Damage的群体
一个群体 Permanent head Damage 的博士生群体 Permanent head Damage Ph.D 博士生一年级的同学们,不要担忧或高兴得太早,抱歉你们还没有经历Qualification——预备考试,你们暂且不能被称为博士,只能称自己是要努力成为博士预备…...
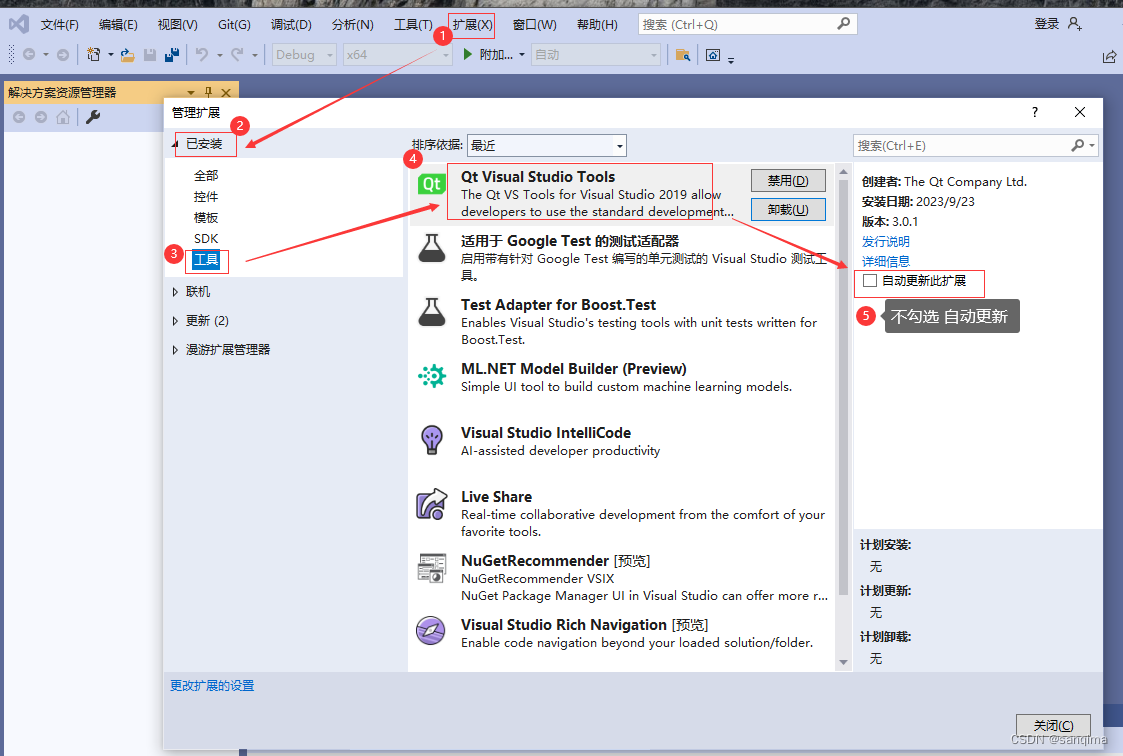
visual studio禁用qt-vsaddin插件更新
visual studio里qt-vsaddin插件默认是自动更新的,由于qt-vsaddin插件新版本的操作方式与老版本相差较大,且新版本不稳定,容易出Bug,所以需要禁用其自动更新,步骤如下: 点击VS2019菜单栏上的【扩展】–…...
Docker通过Dockerfile创建Redis、Nginx--详细过程
创建Nginx镜像 我们先创建一个目录,在目录里创建Dockerfile [rootdocker-3 ~]# mkdir mynginx [rootdocker-3 ~]# cd mynginx [rootdocker-3 ~]# vim Dockerfile Dockerfile的内容 FROM daocloud.io/library/centos:7 RUN buildDepsreadline-devel pcre-devel o…...

关于使用 uniapp Vue3 开发分享页面 语法糖 setup 开发获取ref踩坑
上代码 前端代码 <!-- 分享弹出 --> <uni-popup ref"share" type"share" safeArea backgroundColor"#fff"><uni-popup-share></uni-popup-share> </uni-popup>处理函数 import {onNavigationBarButtonTap} from…...
Springboot+vue的时间管理系统(有报告)。Javaee项目,springboot vue前后端分离项目。
演示视频: Springbootvue的时间管理系统(有报告)。Javaee项目,springboot vue前后端分离项目。 项目介绍: 本文设计了一个基于Springbootvue的前后端分离的时间管理系统,采用M(model࿰…...
企业如何实时监管员工聊天转账行为
你还在担心员工飞单、私单吗? 你还在担心员工辱骂删除客户吗? 你还在担心员工离职会带走公司客户吗? 你还在担心员工工作不认真,工作量无法统计吗? 。。。。。。。。 在当今互联网时代,企业微信的应用已…...
2.2.3.1vim + ctags + cscope + taglist
在window下,我们一般用Source Insight来查看代码而在linux下,使用vim来查看代码,vim是一个简单的文本浏览/编辑器,它可以通过插件的形式,搭建一个完全的类Source Insight环境,通过快捷键的形式,快速查看、定位变量/函数,本文就是基于vim,通过ctags+cscope+taglist+Ner…...

JAVA面经整理(4)
一)Volitaile关键字的作用: 1)保证多线程环境下共享变量的可见性,对于一个线程对于一个共享表变量的修改,其他线程可以立即看到修改之后的共享变量的值 2)可以增加内存屏障来放置多个指令之间的重排序 volatile的使用:常常用于一写多读的情况下ÿ…...

Python3数据科学包系列(一):数据分析实战
Python3中类的高级语法及实战 Python3(基础|高级)语法实战(|多线程|多进程|线程池|进程池技术)|多线程安全问题解决方案 Python3数据科学包系列(一):数据分析实战 Python3数据科学包系列(二):数据分析实战 认识下数据科学中数据处理基础包: (1)NumPy 俗话说: 要学会跑需先…...

【LittleXi】【MIT6.S081-2020Fall】Lab: locks
【MIT6.S081-2020Fall】Lab: locks 【MIT6.S081-2020Fall】Lab: locks内存分配实验内存分配实验准备实验目的1. 举一个例子说明修改前的**kernel/kalloc.c**中如果没有锁会导致哪些进程间竞争(races)问题2. 说明修改前的kernel/kalloc.c中锁竞争contention问题及其后果3. 解释a…...
图像压缩:Transformer-based Image Compression with Variable Image Quality Objectives
论文作者:Chia-Hao Kao,Yi-Hsin Chen,Cheng Chien,Wei-Chen Chiu,Wen-Hsiao Peng 作者单位:National Yang Ming Chiao Tung University 论文链接:http://arxiv.org/abs/2309.12717v1 内容简介: 1)方向:…...

C++ 类和对象篇(四) 构造函数
目录 一、概念 1. 构造函数是什么? 2. 为什么C要引入构造函数? 3. 怎么用构造函数? 3.1 创建构造函数 3.2 调用构造函数 二、构造函数的特性 三、构造函数对成员变量初始化 0. 对构造函数和成员变量分类 1. 带参构造函数对成员变量初始化 2. …...

Swing程序设计(5)绝对布局,流布局
文章目录 前言一、布局管理器二、介绍 1.绝对布局2.流布局总结 前言 Swing窗体中,每一个组件都有大小和具体的位置。而在容器中摆放各种组件时,很难判断其组件的具体位置和大小。即一个完整的界面中,往往有多个组件,那么如何将这…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

比较数据迁移后MySQL数据库和OceanBase数据仓库中的表
设计一个MySQL数据库和OceanBase数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...

在 Spring Boot 项目里,MYSQL中json类型字段使用
前言: 因为程序特殊需求导致,需要mysql数据库存储json类型数据,因此记录一下使用流程 1.java实体中新增字段 private List<User> users 2.增加mybatis-plus注解 TableField(typeHandler FastjsonTypeHandler.class) private Lis…...

spring Security对RBAC及其ABAC的支持使用
RBAC (基于角色的访问控制) RBAC (Role-Based Access Control) 是 Spring Security 中最常用的权限模型,它将权限分配给角色,再将角色分配给用户。 RBAC 核心实现 1. 数据库设计 users roles permissions ------- ------…...

WebRTC调研
WebRTC是什么,为什么,如何使用 WebRTC有什么优势 WebRTC Architecture Amazon KVS WebRTC 其它厂商WebRTC 海康门禁WebRTC 海康门禁其他界面整理 威视通WebRTC 局域网 Google浏览器 Microsoft Edge 公网 RTSP RTMP NVR ONVIF SIP SRT WebRTC协…...

高分辨率图像合成归一化流扩展
大家读完觉得有帮助记得关注和点赞!!! 1 摘要 我们提出了STARFlow,一种基于归一化流的可扩展生成模型,它在高分辨率图像合成方面取得了强大的性能。STARFlow的主要构建块是Transformer自回归流(TARFlow&am…...

【1】跨越技术栈鸿沟:字节跳动开源TRAE AI编程IDE的实战体验
2024年初,人工智能编程工具领域发生了一次静默的变革。当字节跳动宣布退出其TRAE项目(一款融合大型语言模型能力的云端AI编程IDE)时,技术社区曾短暂叹息。然而这一退场并非终点——通过开源社区的接力,TRAE在WayToAGI等…...

大数据驱动企业决策智能化的路径与实践
📝个人主页🌹:慌ZHANG-CSDN博客 🌹🌹期待您的关注 🌹🌹 一、引言:数据驱动的企业竞争力重构 在这个瞬息万变的商业时代,“快者胜”的竞争逻辑愈发明显。企业如何在复杂环…...


