推荐算法——Apriori算法原理
0、前言:
- 首先名字别读错:an pu ruo ao rui 【拼音发音】
- Apriori是一种推荐算法
- 推荐系统:从海量数据中,帮助用户进行信息的过滤和选择。主要推荐方法有:基于内容的推荐、协同过滤推荐、基于关联规则的推荐、基于知识的推荐、混合推荐。
- 关联分析:是一种在大规模数据集中寻找有趣关系的非监督学习算法,是利用一些有趣性的量度来识别数据库中发现的强规则。
1、基础概念
- 频繁项集:经常【需要量化】出现在一块的物品的集合
- 关联规则:暗示两种物品之间可能存在很强的关系
- 事务:将数据看成一条条交易记录的集合,事务就是一条交易
- 项:交易的每一个物品称为一个项
- 项集:包含零个或者多个项的集合
- k-项集:包含k个项的项集
- 前件和后件:一个规则中先买了尿布后买了啤酒,尿布就是啤酒的前件、啤酒就是尿布的后件
- 常用频繁项集的评估标准有:支持度、置信度、提升度;
- 支持度就是几个关联的数据在数据集中出现次数占总数据集的比重。(举例:超市一天卖了5单,其中有2单同时出现了尿布和啤酒,那么{尿布、啤酒}的支持度就是2/5=0.4),支持度常用来删除一些没意义的规则。
- 置信度就是一个数据出现后,另一个数据出现的概率。(举例:买了尿布后会买啤酒的概率=两者同时出现的概率(两者的支持度)/尿布出现的概率(尿布的支持度))
- 提升度:如果A事件的支持度本来就很高,然后求B事件发生后A事件的置信度,发现也很高,但并没有A事件本身的支持度高,就有可能误以为B事件的发生导致A事件发生的可能性增加了。所以加入了提升度的概念(举例:求A事件发生对B事件的提升度=AB同时发生的支持度/B事件发生的持度度),提升度大于1,表明A对B是有效的强关联规则,小于1表明A对B是无效的强关联规则。等于1,说明没有提升。
- ★发现频繁项集和关联规则:如果一一遍历去找关联规则和频繁项集,计算量非常大,所以要进行筛选。
- 1、首先设定最小支持度,最小置信度,找到满足最小支持度的所有项集,这些项集叫做频繁项集。
- 2、从频繁项集中提取所有高置信度的规则,这些规则就是强关联规则。
- 注意:如果一个项集是频繁的,那么它的所有子集也是频繁的。
- 注意:如果一个项集是非频繁的,那么所有包含它的集合也是非频繁的。【通过这条规则减少计算量】
2、算法实现过程
- Apriori算法原理:所有非频繁项集不用计算,减少计算量。获取apriori频繁项集是第一步,要通过apriori最终获取强关联规则,就要在频繁项集支持度的基础上,计算每种规则的支持度。

- 原始候选集构建1-项集:
# 数据集
dataset = [[1, 3, 4], [2, 3, 5], [1, 2, 3, 5], [2, 5]]
# 让候选集每一项变成不可变集合,进而获取1-项集
def creat_c1(data_set):c1 = []for data in data_set:for i in data:if i not in c1:c1.append(i)c1.sort()return list(map(frozenset,[{i} for i in c1])) # frozenset是将集合变成不可变集合,目的是最后让frozenset作为字典的key
c1 = creat_c1(dataset)
'''
[frozenset({1}),frozenset({2}),frozenset({3}),frozenset({4}),frozenset({5})]
'''
- 由1-项集(C1)转为1-项频繁集(L1)推出k-项集转k-项频繁集的函数:通过支持度筛选频繁集;scanD()函数:获取所有k-项集的支持度和k-项集对应的k-项频繁集
# C1(1项集):L1(1项频繁项集)
# D:数据集
# Ck:k项集
# min_support:最小支持度
def scanD(D,Ck,min_support=0.1):support_dic = {}# 遍历原始交易记录for d in D:for c in Ck:# 判断是否是子集,是的话数量加1if c.issubset(d):support_dic[c] = support_dic.get(c,0) + 1 # 防止刚开始support_dic是空support_data = {} # 所有项集的支持度LK = [] # 频繁项集# 计算支持度for k,v in support_dic.items():support = v/len(D)support_data[k] = support
# print(support_data) # 打印支持度# 获得频繁项集if support >= min_support:LK.append(k)# 返回频繁项集、所有项集支持度:return LK, support_data
- 由1-项频繁集产生2-项集的方法推出:k-项频繁集产生k+1-项集的方法;apriori_gen()函数:获取所有k-项频繁集(Lk)对应的k+1-项集(Ck+1),如下图以2-项集生成方法说明:

# L1(1频繁项集) => C2(2项集)
def apriori_gen(LK):Ck = []for i in range(len(LK)-1):for j in range(i+1,len(LK)):f_set = LK[i] | LK[j]# print(f_set)# 不能重复,新项集只能是k+1项if f_set not in Ck and len(f_set) == len(LK[0])+1:Ck.append(f_set)# print(Ck)return Ck
- 获取频繁项集和频繁项集生成过程中产生的项集的支持度
import time
def apriori(D, min_support=0.1):c1 = creat_c1(D)L1,support1 = scanD(D,c1,min_support)# 所有频繁项集L_f = []# 所有项集支持度就直接添加到support1中# 循环while True:L_f.append(L1)# 项集C = apriori_gen(L1)# 项集——频繁项集L,support = scanD(D,C,min_support)L1 = Lsupport1.update(support)if len(L1)==0:breakreturn L_f,support1
- 获取k项集满足最小置信度的强关联规则的集合
计算置信度:confidence(X -> Y) = P(Y|X) = P(XY) / P(X)【在x发生的条件下Y发生的置信度】
calculate_conf()函数:计算某个频繁项集对应的满足最小置信度的强关联规则的集合。
# 计算一个项集的所有强关联规则
# 计算置信度
# freqSet: 频繁项集
# H=[frozenset({i}) for i in freqSet]
# L, support_Data = apriori(dataset, min_support=n)
# brl = [ ] # 保存强关联规则的列表
def calculate_conf(freqSet, H, supportData, brl, minConf=0.5):newH = [ ]# 遍历Hfor s in H:# 置信度conf = supportData[freqSet] / supportData[freqSet - s]# conf(3,5->1) = P(1, 3, 5) / P(3,5) # display(f'--- {freqSet - s} -> {s} = {conf} ---')# 大于最小置信度的规则是强规则if conf >= minConf:# 保存强关联规则到brl中brl.append( (freqSet - s, "->" , s, ' = ', conf) ) newH.append(s)return newH用一个2-项集测试下函数calculate_conf,发现对于2-项集,函数能够获取所有满足置信度要求的关联规则。
freqSet = frozenset({1, 3})
H = [frozenset({i}) for i in freqSet]
L, support_data = apriori(dataset, min_support=0.2)
brl = [ ] # 保存强关联规则的列表
# display(freqSet, H)# 计算单个项集的置信度
calculate_conf(freqSet, H, support_data, brl, minConf=0.1)
brl
'''
[(frozenset({3}), '->', frozenset({1}), ' = ', 0.6666666666666666),(frozenset({1}), '->', frozenset({3}), ' = ', 1.0)]
'''
# 3-项集
freqSet = frozenset({1, 3, 5})
H = [frozenset({i}) for i in freqSet]
L, support_data = apriori(dataset, min_support=0.2)
brl = [ ] # 保存强关联规则的列表
# display(freqSet, H)# 计算单个项集的置信度
calculate_conf(freqSet, H, support_data, brl, minConf=0.1)
brl
'''
[(frozenset({3, 5}), '->', frozenset({1}), ' = ', 0.5),(frozenset({1, 5}), '->', frozenset({3}), ' = ', 1.0),(frozenset({1, 3}), '->', frozenset({5}), ' = ', 0.5)]
'''
可以发现:在3项集中出现了问题,3项集中只有2-项集作为前件的情况,没有1-项集作为前件的情况,出现了统计不完全的情况。因此为了让统计结果齐全,需要重新写个函数完善calculate_conf()函数。
# 考虑2-项集,3-项集,4-项集...
def rules_from_freq(freqSet, H, supportData, brl, minConf=0.7):tmp = Truewhile tmp:tmp = False# 计算置信度newH = calculate_conf(freqSet, H, supportData, brl, minConf=minConf)# display(f'newH: {newH}')H = apriori_gen(newH)# display(f'H: {H}')# print('*' * 100)tmp = not (H==[ ] or len(H[0]) == len(freqSet))测试:通过测试结果可以看出,完善之后的函数就能够获得所有满足要求置信度的关联规则
# 3-项集
freqSet = frozenset({1, 3, 5})
H = [frozenset({i}) for i in freqSet]
L, support_data = apriori(dataset, min_support=0.2)
brl = [ ] # 保存强关联规则的列表
# display(freqSet, H)# 计算单个项集的置信度
rules_from_freq(freqSet, H, support_data, brl, minConf=0.1)
brl
'''
[(frozenset({3, 5}), '->', frozenset({1}), ' = ', 0.5),(frozenset({1, 5}), '->', frozenset({3}), ' = ', 1.0),(frozenset({1, 3}), '->', frozenset({5}), ' = ', 0.5),(frozenset({5}), '->', frozenset({1, 3}), ' = ', 0.3333333333333333),(frozenset({3}), '->', frozenset({1, 5}), ' = ', 0.3333333333333333),(frozenset({1}), '->', frozenset({3, 5}), ' = ', 0.5)]
'''
- 获取强关联规则的置信度:获取给定项集L中满足置信度要求的强关联规则
def gen_rules(L, support_data, min_conf=0.5):big_rule_list = [ ]for i in range(1, len(L)): # 遍历所有行,第一行除外for freqSet in L[i]: # 遍历每一行的所有元素# display(freqSet)H = [frozenset({i}) for i in freqSet]# 求每个项集的强关联规则,会保存在big_rule_list中rules_from_freq(freqSet, H, support_data, big_rule_list, minConf=min_conf)return big_rule_list
3、apriori算法总结:通过总结疏通下apriori算法中求频繁项集和求强关联规则的函数构造方法

相关文章:

推荐算法——Apriori算法原理
0、前言: 首先名字别读错:an pu ruo ao rui 【拼音发音】Apriori是一种推荐算法推荐系统:从海量数据中,帮助用户进行信息的过滤和选择。主要推荐方法有:基于内容的推荐、协同过滤推荐、基于关联规则的推荐、基于知识的…...

vue ant 隐藏 列
vue ant 隐藏 列 如果你使用的是Vue和Ant Design Vue组件库,你可以使用v-if指令来实现条件渲染来隐藏列。以下是一个示例代码: <template><a-table :columns"columns" :data-source"data"><template v-slot:custom…...

java基础之初始化顺序
初始化顺序 在类中变量定义的顺序决定了它们初始化的顺序。在创建任何java对象时,都是依次调用父类非静态初始化块、父类构造器执行初始化、本类的非静态初始化块、本类构造器执行初始化 public class House { // 构造器之前 Window w1 new Window(1); Ho…...
FFmpeg 命令:从入门到精通 | ffmpeg filter(过滤器 / 滤镜)
FFmpeg 命令:从入门到精通 | ffmpeg filter(过滤器 / 滤镜) FFmpeg 命令:从入门到精通 | ffmpeg filter(过滤器 / 滤镜)ffmpeg fliter 基本内置变量视频裁剪文字水印图片水印画中画视频多宫格处理 FFmpeg 命…...

【C语言】23-结构体类型
目录 1. 如何建立结构体类型2. 如何使用结构体2.1 定义结构体变量2.2 结构体变量的初始化和引用2.3 结构体数组2.4 结构体指针2.4.1 指向结构体变量的指针2.4.2 指向结构体数组的指针C 语言提供了一些由系统已定义好的数据类型,如: int、 float、 char 等,用户可以在程序…...

Python小技巧:快速合并字典dict()
文章目录 前言知识点字典合并1. dict.update()基础合并2. 字典推导式 update() 后话 前言 这里是Python小技巧的系列文章。这是第四篇,快速合并字典。 在Python的使用中,有时候需要将两个 dict(字典) 进行合并。 通常我们会借助 dict(字典) 的内置方法 …...
)
如何使用 React 和 Docusaurus 编写的一些自定义钩子(Hook)
import useRouteContext from @docusaurus/useRouteContext; import {DependencyList, useEffect, useRef, useState, useMemo } from react; import {dequal } from dequal; /* eslint-disable global-require */ // @ts-ignore/*** 用于深度检测依赖的useMemo钩子* @param fa…...

【初识Linux】Linux环境配置、Linux的基本指令 一
Linux基本指令一 一、学习前提(环境配置)①安装Xshell和云服务器推荐②Xshell用途如下图③打开Xshell 二、 Linux基本指令①whoami和who指令②pwd、ls、ls -l三个指令ls指令扩充 ③cd指令前提了解有了上面的认识,我们就可以开始cd指令的学习了 ④tree指令…...

conda常用命令参数,指定版本,依赖库文件,创建虚拟环境,删除,激活,退出,内部安装包,pip通过代理安装包
以下是conda的常用命令和参数: 1. 创建虚拟环境: - 创建一个新的虚拟环境:conda create -n 环境名 pythonx.x - 使用指定的依赖文件创建虚拟环境:conda create -n 环境名 --file requirements.txt 2. 激活虚拟环境&#x…...
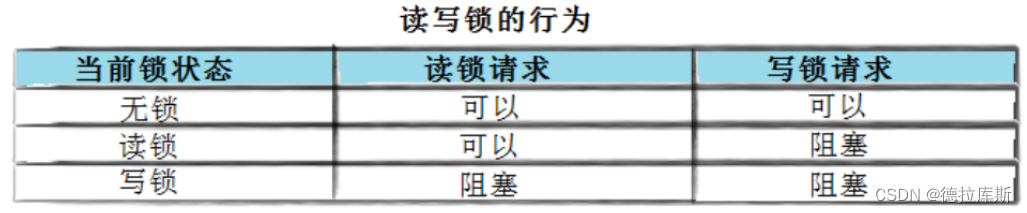
【锁的区别】C++线程库和POSIX线程库锁的区别
C线程库和POSIX线程库锁的区别 C线程库代码段的互斥:mutex、recursive_mutex、timed_mutex、recursive_timed_mutex互斥量mutex:直接进行lock()或者unlock()递归互斥锁recursive_mutex:可以多次加锁,意味着加几次锁就需要解几次锁…...

网络层·IP协议
承接前文TCP协议-CSDN博客 简介 协议头格式 网段划分(重要) 划分方法 IP地址的数量限制(背景介绍) 私有IP地址和公网IP地址(提出解决思路) NAT技术(解决方法) 路由 网络层 在复杂的网络环境中确定一个合适的路径 IP协议 主机: 配有IP地址, 可以认为就是你的电脑; 路由器:…...
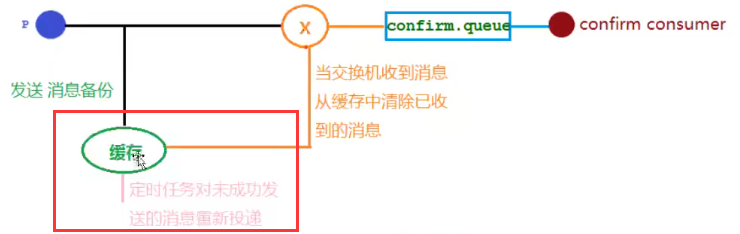
RabbitMQ学习笔记(下):延迟队列,发布确认高级,备份交换机
十、延迟队列 延迟队列 概念: 延迟队列使用场景: 流程图: 延迟队列整合Springboot 导入依赖: <dependencies><dependency><groupId>org.springframework.boot</groupId><artifactId>spring-boot…...

Python 无废话-基础知识面向对象编程详解
类定义 如何理解万物皆对象? 生活中一些事物,动物(可爱的小狗、调皮的小猫)、交通工具(比亚迪U8汽车、飞机)、人(学生、教师)…… 这些对象都有着独特或共性的属性和方法来描述其…...
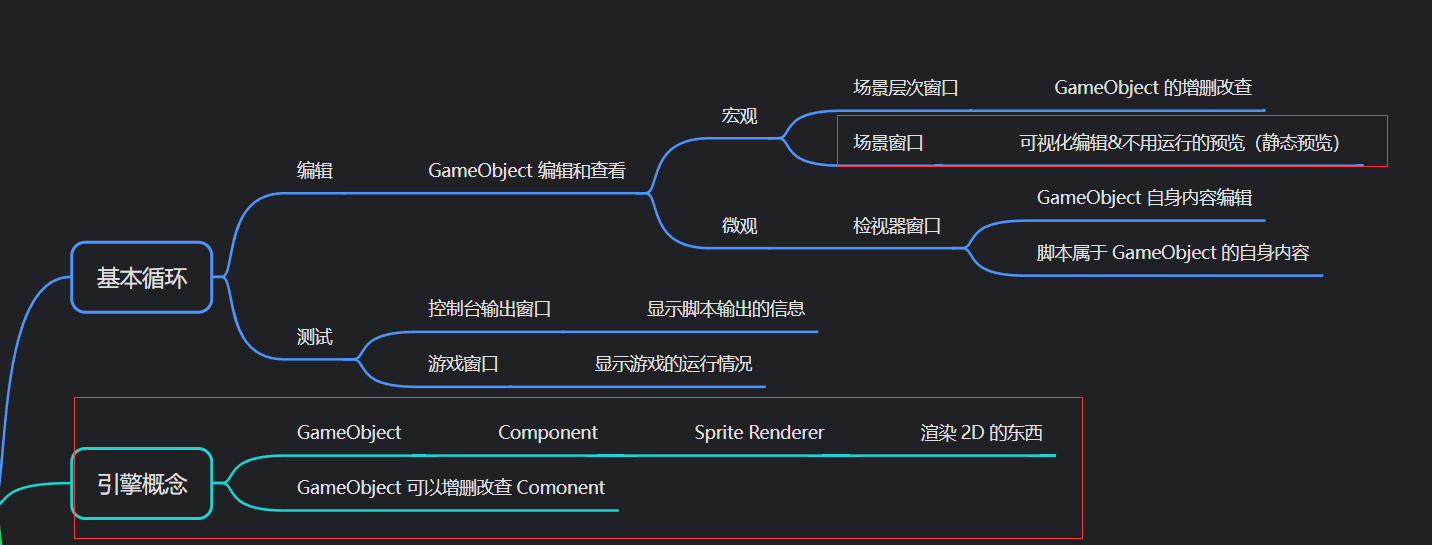
凉鞋的 Unity 笔记 106. 第二轮循环场景视图Sprite Renderer
106. 第二轮循环&场景视图&Sprite Renderer 从这一篇开始,我们开始进行第二轮循环。 这次我们至少能够在游戏运行窗口看到一些东西。 首先还是在场景层次窗口进行编辑,先创建一个 Sprite,操作如下: 创建后,会在 Scene …...

Vue中如何进行分布式路由配置与管理
Vue中的分布式路由配置与管理 随着现代Web应用程序的复杂性不断增加,分布式路由配置和管理成为了一个重要的主题。Vue.js作为一种流行的前端框架,提供了多种方法来管理Vue应用程序的路由。本文将深入探讨在Vue中如何进行分布式路由配置与管理࿰…...
Solidity 合约漏洞,价值 38BNB 漏洞分析
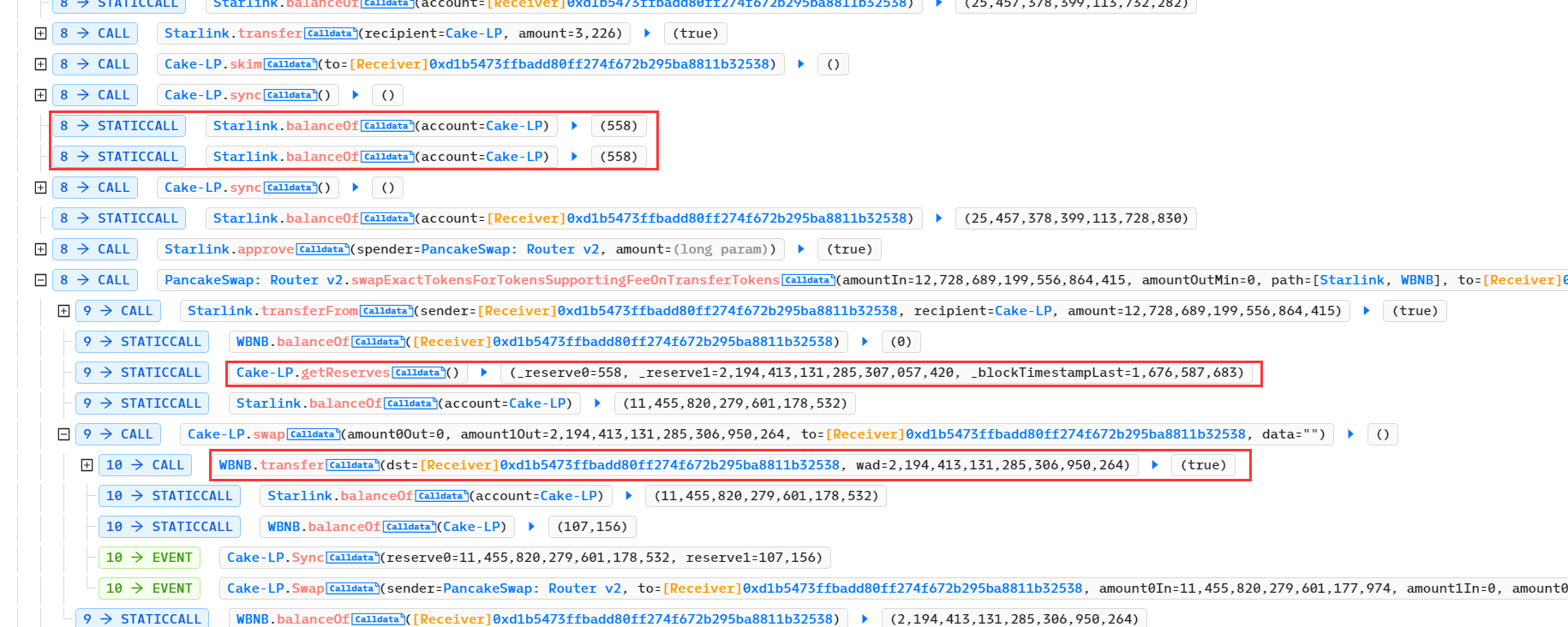
Solidity 合约漏洞,价值 38BNB 漏洞分析 1. 漏洞简介 https://twitter.com/NumenAlert/status/1626447469361102850 https://twitter.com/bbbb/status/1626392605264351235 2. 相关地址或交易 攻击交易: https://bscscan.com/tx/0x146586f05a451313…...
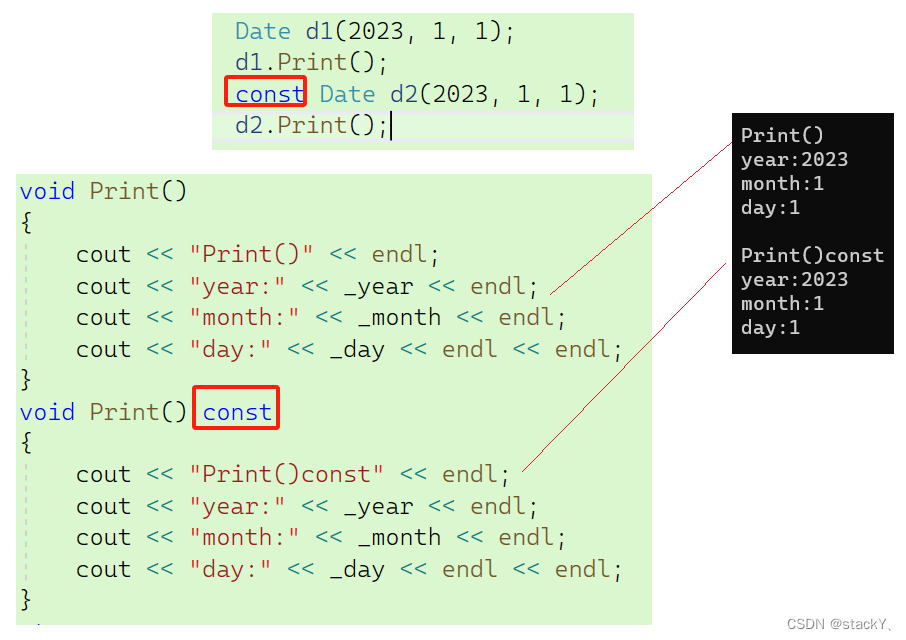
【C++】:类和对象(2)
朋友们、伙计们,我们又见面了,本期来给大家解读一下有关Linux的基础知识点,如果看完之后对你有一定的启发,那么请留下你的三连,祝大家心想事成! C 语 言 专 栏:C语言:从入门到精通 数…...

【GIT版本控制】--提交更改
一、添加文件到暂存区 在GIT中,要提交更改,首先需要将文件添加到暂存区(Staging Area)。这是一个用于存放将要提交的更改的临时区域。以下是将文件添加到暂存区的步骤: 打开终端或命令提示符:首先&#x…...
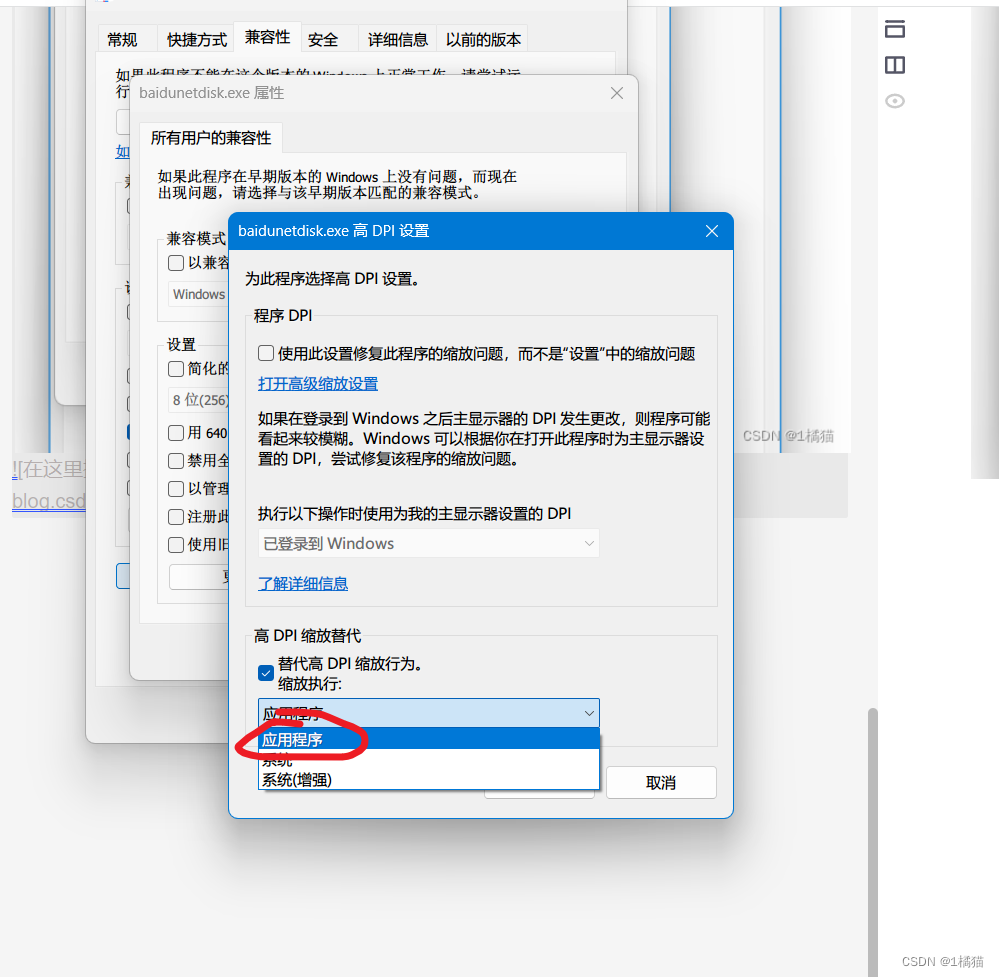
解决高分屏DPI缩放PC端百度网盘界面模糊的问题
第一步 更新最新版本 首先,在百度网盘官网下载最新安装包: https://pan.baidu.com/download 进行覆盖安装 第二步 修改兼容性设置 右键百度网盘图标,点击属性,在兼容性选项卡中点击更改所有用户的设置 弹出的选项卡中选择更改高…...
全能视频工具 VideoProc Converter 4K for mac中文
VideoProc 4K提供快速完备的4K影片处理方案,您可以透过这款软体调节输出影片格式和大小。能够有效压缩HD/4K影片体积90%以上,以便更好更快地上传到YouTube,或是通过电子邮件附件发送。业界领先的视讯压缩引擎,让你轻松处理大体积视…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

2025年渗透测试面试题总结-腾讯[实习]科恩实验室-安全工程师(题目+回答)
安全领域各种资源,学习文档,以及工具分享、前沿信息分享、POC、EXP分享。不定期分享各种好玩的项目及好用的工具,欢迎关注。 目录 腾讯[实习]科恩实验室-安全工程师 一、网络与协议 1. TCP三次握手 2. SYN扫描原理 3. HTTPS证书机制 二…...
)
C++课设:简易日历程序(支持传统节假日 + 二十四节气 + 个人纪念日管理)
名人说:路漫漫其修远兮,吾将上下而求索。—— 屈原《离骚》 创作者:Code_流苏(CSDN)(一个喜欢古诗词和编程的Coder😊) 专栏介绍:《编程项目实战》 目录 一、为什么要开发一个日历程序?1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...
