eigen::Affine3d 转换
平移eigen::vector3d和四元数Eigen::Quaterniond 转 eigen::Affine3d
Eigen::Vector3d t = Eigen::Vector3d::Zero();
Eigen::Quaterniond q = Eigen::Quaterniond ::Identity();Eigen::Affine3d affine3d = t * q.toRotationMatrix();Eigen::Matrix4d 转 eigen::Affine3d
Eigen::Matrix4d mat = Eigen::Matrix4d::Identity();
Eigen::Affine3d transform = Eigen::Affine3d::Identity();
transform.matrix() = mat; 这里主要是用于点云加速,pcl自带的点云变换包含指令集优化,如下:
template <typename PointT, typename Scalar> inline PointTtransformPoint (const PointT &point, const Eigen::Transform<Scalar, 3, Eigen::Affine> &transform){PointT ret = point;pcl::detail::Transformer<Scalar> tf (transform.matrix ());tf.se3 (point.data, ret.data);return (ret);}Point Cloud Library (PCL): pcl/common/impl/transforms.hpp Source File
相关文章:

eigen::Affine3d 转换
平移eigen::vector3d和四元数Eigen::Quaterniond 转 eigen::Affine3d Eigen::Vector3d t Eigen::Vector3d::Zero(); Eigen::Quaterniond q Eigen::Quaterniond ::Identity();Eigen::Affine3d affine3d t * q.toRotationMatrix(); Eigen::Matrix4d 转 eigen::Affine3d Eige…...
【Python从入门到进阶】38、selenium关于Chrome handless的基本使用
接上篇《37、selenium关于phantomjs的基本使用》 上一篇我们介绍了有关phantomjs的相关知识,但由于selenium已经放弃PhantomJS,本篇我们来学习Chrome的无头版浏览器Chrome Handless的使用。 一、Chrome Headless简介 Chrome Headless是一个无界面的浏览…...
)
给Python项目创建一个虚拟环境(enev)
给Python项目创建一个虚拟环境(enev) 为您的Python项目创建一个虚拟环境是一种良好的实践,可以隔离项目的依赖项,以确保它们不会干扰全局Python环境或其他项目。您可以使用venv模块来创建虚拟环境。以下是在Linux上创建虚拟环境的…...

【RK3588】YOLO V5在瑞芯微板子上部署问题记录汇总
YOLO V5训练模型部署到瑞芯微的板子上面,官方是有给出案例和转过详情的。并且也提供了Python版本的推理代码,以及C语言的代码。 但是,对于转换过程中的细节,哪些需要改?怎么改?如何改,和为什么…...

别人做的百度百科词条信息不全,如何更正自己的百度百科词条
很多人自己的百度百科词条是别人上传上去的,自己压根不知道,而且里面的信息内容要么不全,要么是有错漏的,但自己想要更正自己的百度百科词条又不知道如何更正,下面洛希爱做百科网和大家介绍一些百科经验知识。 首先百…...
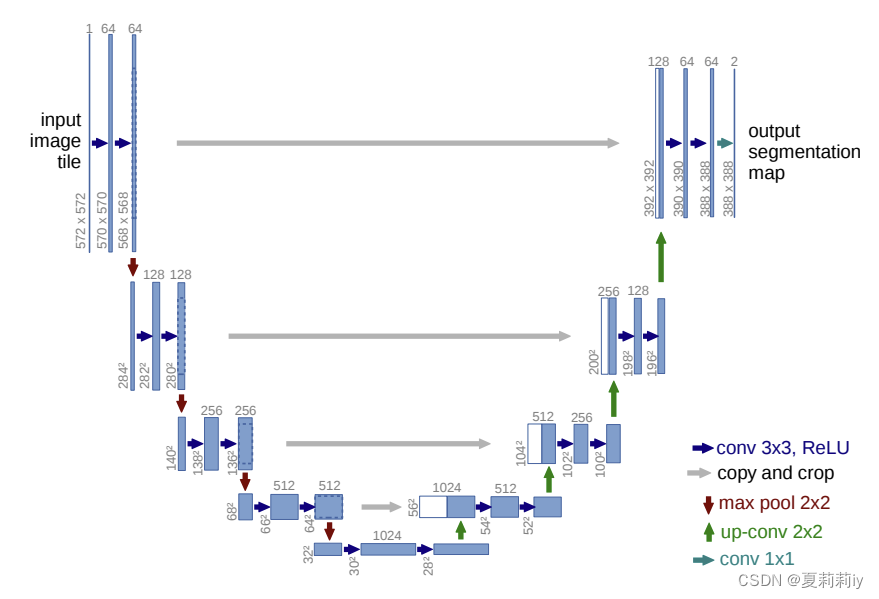
[论文精读]U-Net: Convolutional Networks for BiomedicalImage Segmentation
论文原文:U-Net: Convolutional Networks for Biomedical Image Segmentation (arxiv.org) 英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔…...
Godot Identifier “File“ not declared in the current scope.
解决方案: f FileAccess.open(savedir, FileAccess.READ)...

Java ORM Bee,多表关联更新
Bee V2.1.8 增加支持多表的update, insert, delete; 使用FK注解进行关联. 如果子实体没有用上FK声明的字段(即FK的字段没有值),则不执行,防止更新到多余记录 外键有一个没有设置时,跳过。 更多实例,请查看样例工程:https://gitee.com/automvc/bee-exam 或:h…...

Java 读取excel文件
导入: 先导入依赖: <!-- 文件上传 --> <dependency><groupId>org.apache.httpcomponents</groupId><artifactId>httpmime</artifactId><version>4.5.7</version> </dependency> <!-- JSON -…...
:数据分析 | 数据挖掘 | 十大算法之一)
PageRank(上):数据分析 | 数据挖掘 | 十大算法之一
⭐️⭐️⭐️⭐️⭐️欢迎来到我的博客⭐️⭐️⭐️⭐️⭐️ 🐴作者:秋无之地 🐴简介:CSDN爬虫、后端、大数据领域创作者。目前从事python爬虫、后端和大数据等相关工作,主要擅长领域有:爬虫、后端、大数据开发、数据分析等。 🐴欢迎小伙伴们点赞👍🏻、收藏⭐️、…...

吃鸡达人专享!提高战斗力,分享干货,查询装备皮肤,保护账号安全!
大家好!作为专业吃鸡行家,我将为您带来一些热门话题和实用内容,帮助您提升游戏战斗力,分享顶级游戏作战干货,并提供便捷的作图工具和查询服务。让我们一起享受吃鸡的乐趣! 首先,我要推荐一款绝地…...
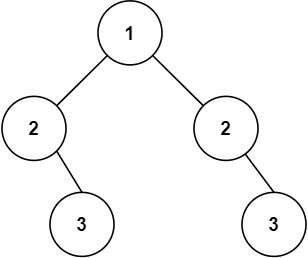
力扣第101题 c++ 递归 迭代 双方法 +注释 ~
题目 101. 对称二叉树 简单 给你一个二叉树的根节点 root , 检查它是否轴对称。 示例 1: 输入:root [1,2,2,3,4,4,3] 输出:true示例 2: 输入:root [1,2,2,null,3,null,3] 输出:false提示&a…...
Go:实现SMTP邮件发送订阅功能(包含163邮箱、163企业邮箱、谷歌gmail邮箱)
需求很简单,就是用户输入自己的邮箱后,使用官方邮箱给用户发送替邮件模版 目录 前置邮件模版邮箱开启SMTP服务163邮箱163企业邮箱谷歌gmail邮箱腾讯企业邮箱-失败其他邮箱-未操作 邮件发送核心代码config.yaml配置读取邮件相关配置发送邮件 附录 前置 邮…...
Scala第十六章节
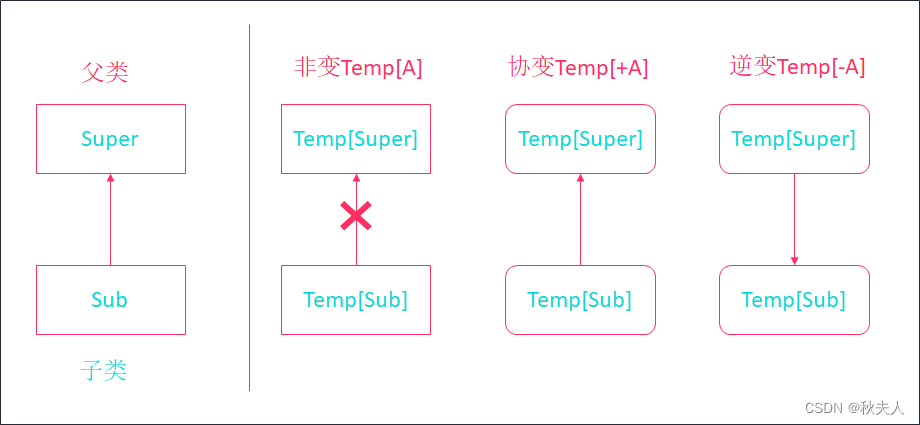
Scala第十六章节 scala总目录 文档资料下载 章节目标 掌握泛型方法, 类, 特质的用法了解泛型上下界相关内容了解协变, 逆变, 非变的用法掌握列表去重排序案例 1. 泛型 泛型的意思是泛指某种具体的数据类型, 在Scala中, 泛型用[数据类型]表示. 在实际开发中, 泛型一般是结合…...

C语言 实现 链 显示 效果 查找 修改 删除
显示所有信息 2023年10月1日的描述:今天放假 2023年10月2日的描述:今天有体育 2023年10月3日的描述:今天有数学 2023年10月4日的描述:今天有语文 2023年10月5日的描述:今天有政治 2023年10月6日的描述:今天交学费 2023年10月7日的描述:今天周末 2023年10月8日的描述:今天给家里…...

CSS基础语法第一天
目录 一、CSS 简介 1.1 CSS简介 1.2 CSS语法 1.3 CSS 语法规范 1.4 CSS 代码风格 1.4.1 样式格式书写 1.4.2 样式大小写 1.4.3 空格规范 二、CSS 基础选择器 2.1选择器分类 2.2标签选择器 2.3 类选择器 2.4 id选择器 2.5 通配符选择器 三、盒子尺寸和背景色 …...

Leetcode 1492.n的第k个因子
给你两个正整数 n 和 k 。 如果正整数 i 满足 n % i 0 ,那么我们就说正整数 i 是整数 n 的因子。 考虑整数 n 的所有因子,将它们 升序排列 。请你返回第 k 个因子。如果 n 的因子数少于 k ,请你返回 -1 。 示例 1: 输入&#…...
十一工具箱流量主小程序源码
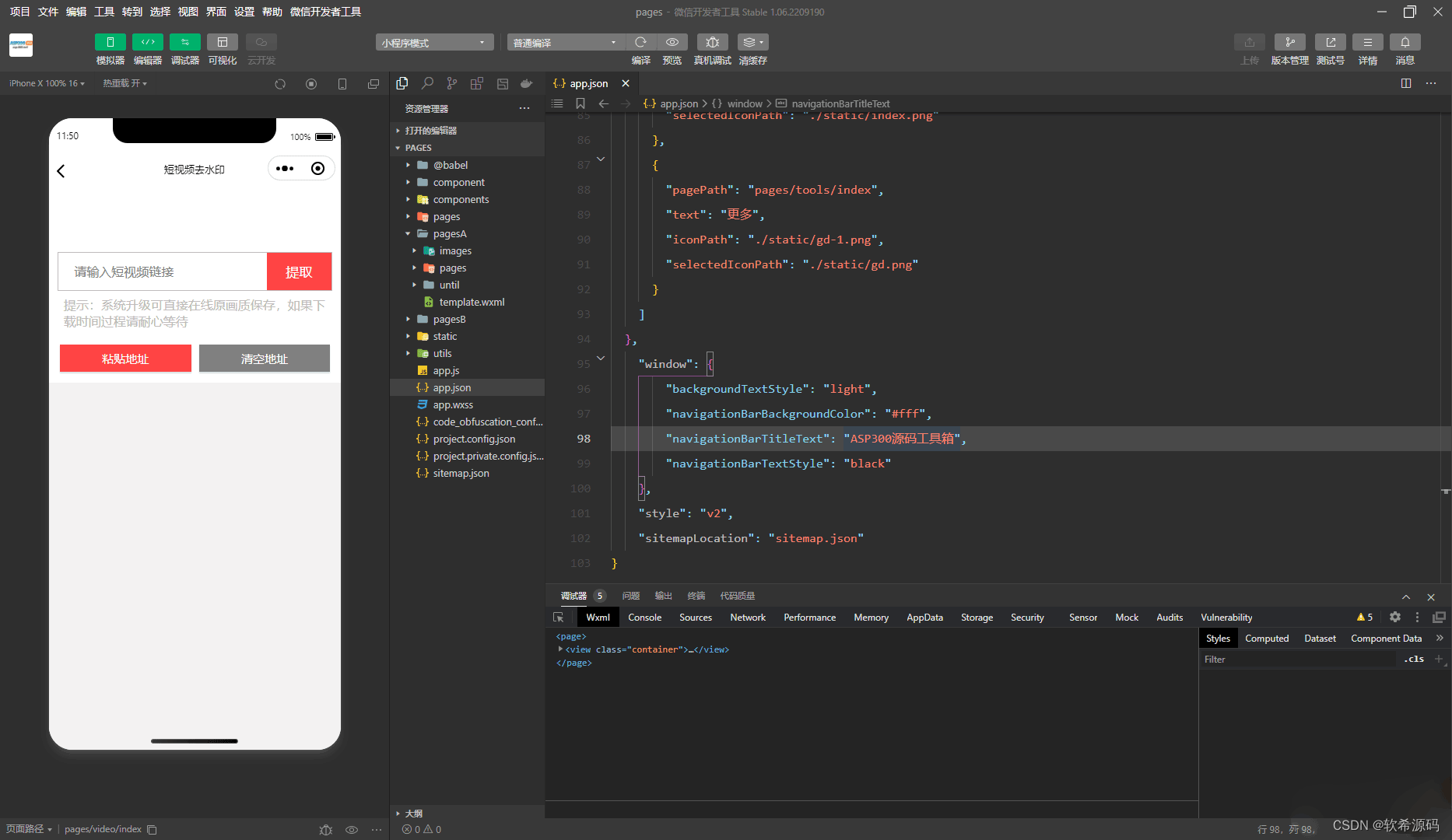
无授权,去过滤机制版本 看到网上发布的都是要授权的 朋友叫我把他去授权,能用就行 就把过滤去了 这样就不用授权 可以免费使用 白嫖党专属 一切接口可用,无需担心不能用 授权者不关站一直可以用 源码下载:https://download.csdn.…...
10.5汇编语言整理
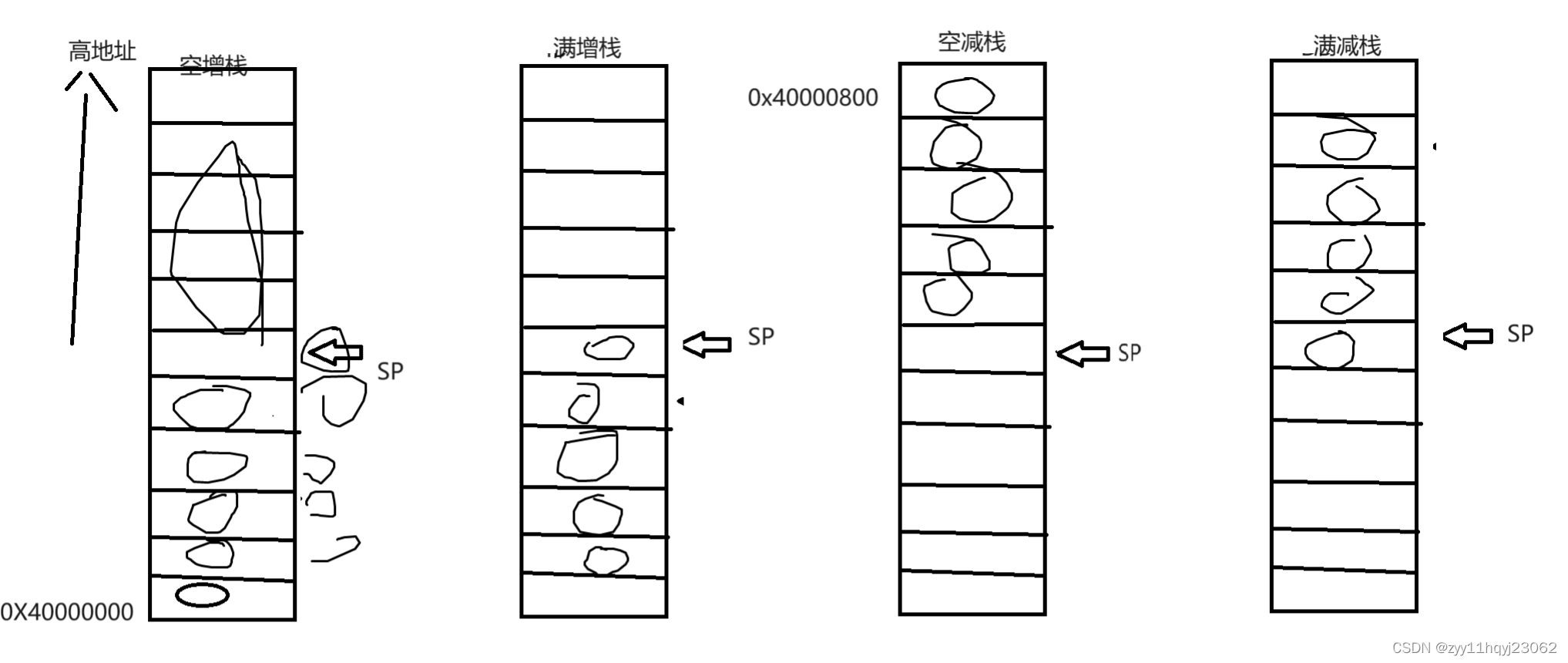
【汇编语言相关语法】 1.汇编语言的组成部分 1.伪操作:不参与程序的执行,但是用于告诉编译器程序该怎么编译 .text .global .end .if .else .endif .data 2.汇编指令 编译器将一条汇编指令编译成一条机器码,在内存里一条指令占4字节内存&…...

Connect to 127.0.0.1:1080 [/127.0.0.1] failed: Connection refused: connect
报错信息 A problem occurred configuring root project CourseSelection. > Could not resolve all artifacts for configuration :classpath.> Could not resolve com.android.tools.build:gradle:3.6.1.Required by:project :> Could not resolve com.android.tool…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

接口自动化测试:HttpRunner基础
相关文档 HttpRunner V3.x中文文档 HttpRunner 用户指南 使用HttpRunner 3.x实现接口自动化测试 HttpRunner介绍 HttpRunner 是一个开源的 API 测试工具,支持 HTTP(S)/HTTP2/WebSocket/RPC 等网络协议,涵盖接口测试、性能测试、数字体验监测等测试类型…...

(一)单例模式
一、前言 单例模式属于六大创建型模式,即在软件设计过程中,主要关注创建对象的结果,并不关心创建对象的过程及细节。创建型设计模式将类对象的实例化过程进行抽象化接口设计,从而隐藏了类对象的实例是如何被创建的,封装了软件系统使用的具体对象类型。 六大创建型模式包括…...

Ubuntu系统复制(U盘-电脑硬盘)
所需环境 电脑自带硬盘:1块 (1T) U盘1:Ubuntu系统引导盘(用于“U盘2”复制到“电脑自带硬盘”) U盘2:Ubuntu系统盘(1T,用于被复制) !!!建议“电脑…...

机器学习的数学基础:线性模型
线性模型 线性模型的基本形式为: f ( x ) ω T x b f\left(\boldsymbol{x}\right)\boldsymbol{\omega}^\text{T}\boldsymbol{x}b f(x)ωTxb 回归问题 利用最小二乘法,得到 ω \boldsymbol{\omega} ω和 b b b的参数估计$ \boldsymbol{\hat{\omega}}…...

leetcode73-矩阵置零
leetcode 73 思路 记录 0 元素的位置:遍历整个矩阵,找出所有值为 0 的元素,并将它们的坐标记录在数组zeroPosition中置零操作:遍历记录的所有 0 元素位置,将每个位置对应的行和列的所有元素置为 0 具体步骤 初始化…...
