王道考研计算机组成原理——计算机硬件的基础知识
计算机组成原理的基本概念
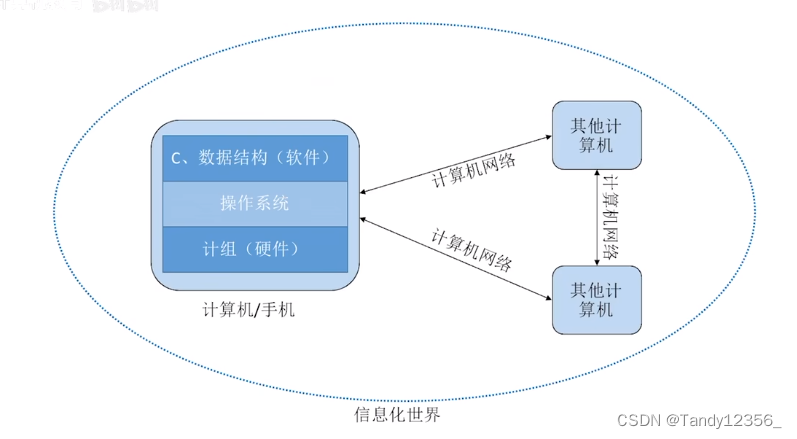
计算机硬件的针脚都是用来传递信息，传递数据用的：
服务程序包含一些调试程序：
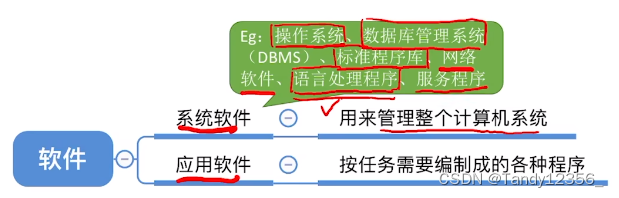
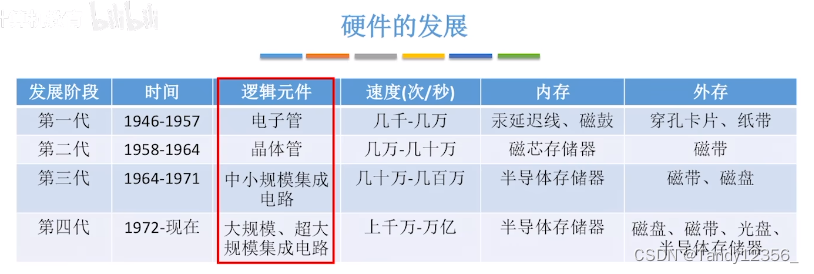
计算机硬件的基本组成
控制器通过电信号来协调其他部件的工作，同时负责解析存储器里存放的程序指令，然后指挥运算器执行相应的加减乘除之类的运算
同一个功能既能用硬件来实现，也能够用软件来实现
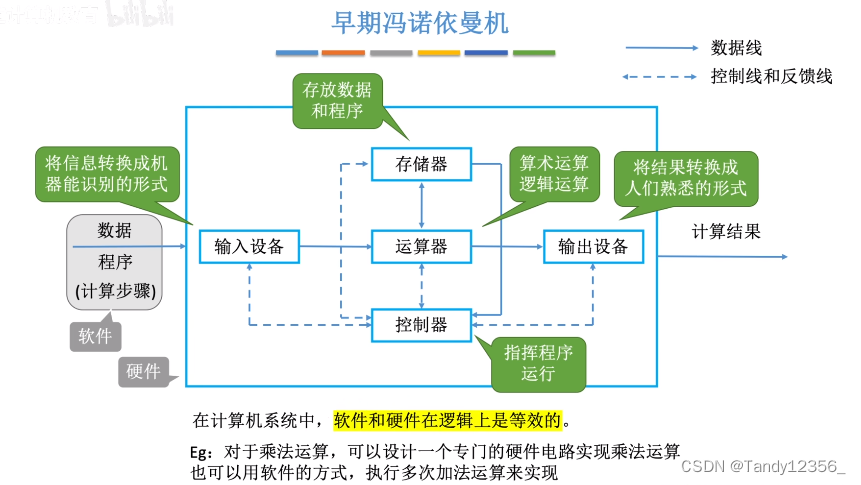
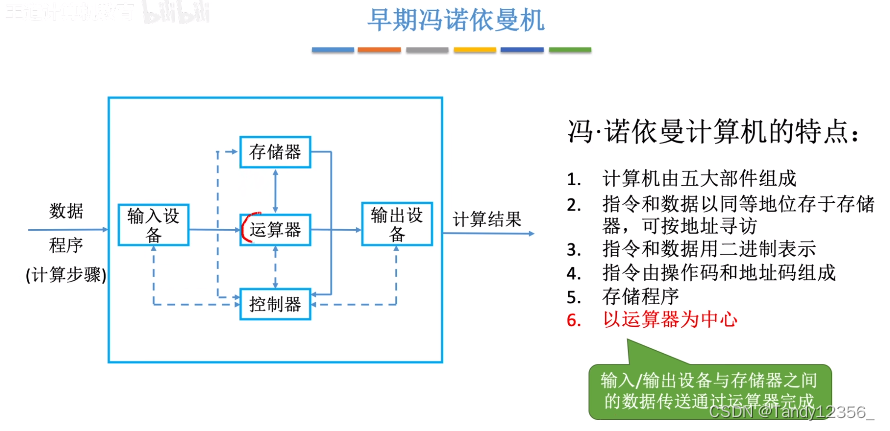
参与运算的数据放到运算器当中，指令放到控制器当中，由控制器来解析这条指令的含义
主存储器的基本组成：
CPU发出一个读/写命令，把地址放到MAR当中，把数据放到MDR当中（相当于菜鸟驿站的柜台，存储体：货架，MAR：取件码）
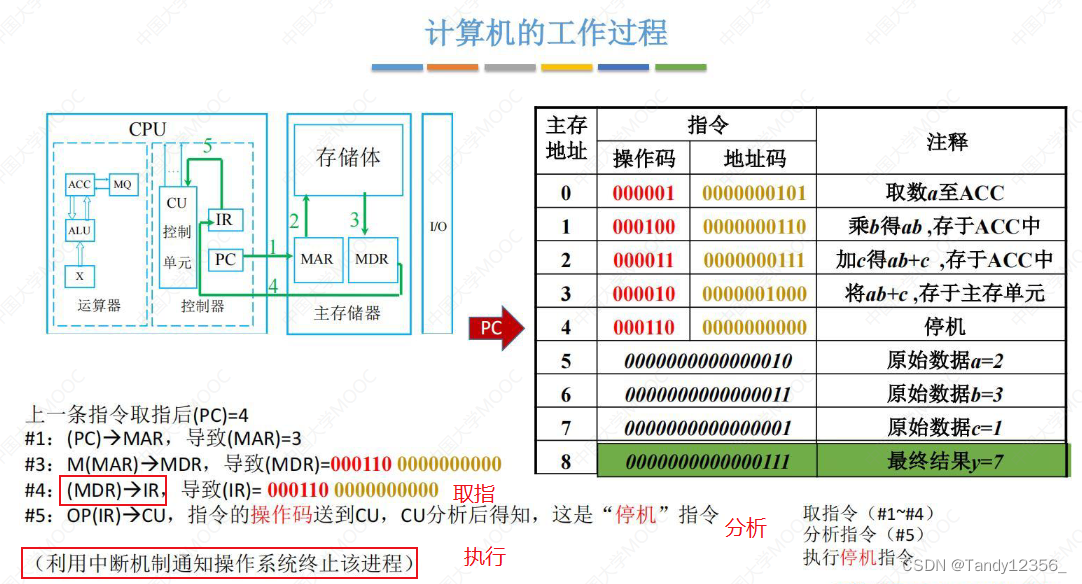
计算机执行一条指令的全过程
cpu会自动把指令拆解成操作码和地址码
最终的结果是ACC寄存器里面的值变成了2
取指令（IR）》解析指令（CU）》执行指令（ALU）
控制单元CU给ALU发出一个信号，告诉他你这次要执行的是乘法操作
5：把操作码放到CU当中分析，发现是存数的指令；
CU后面通过控制总线告诉主存储器本次执行的操作是存数操作
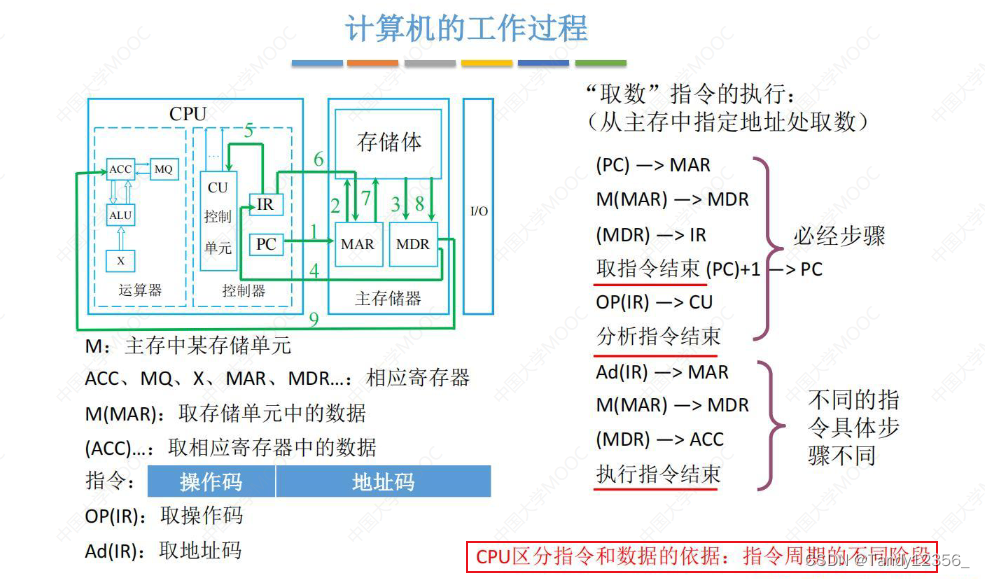
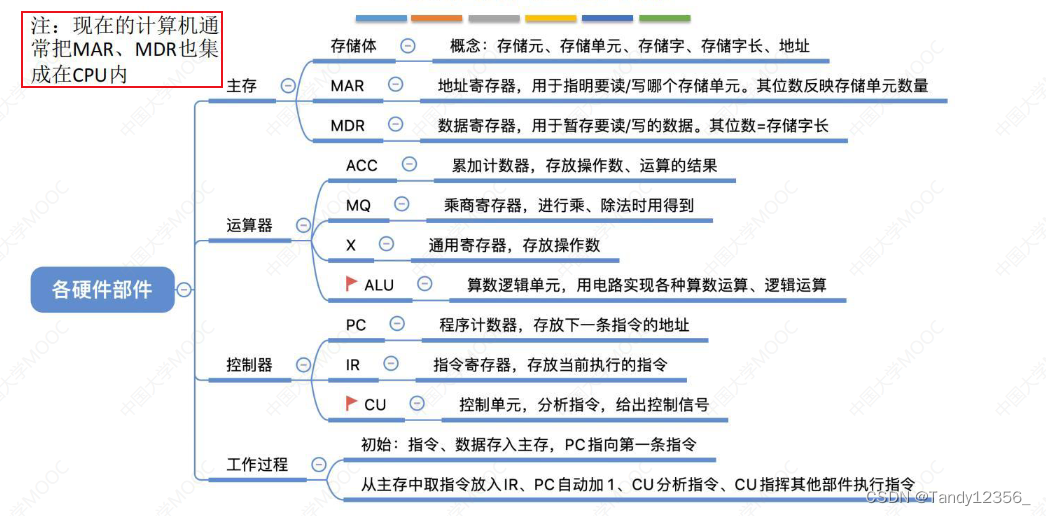
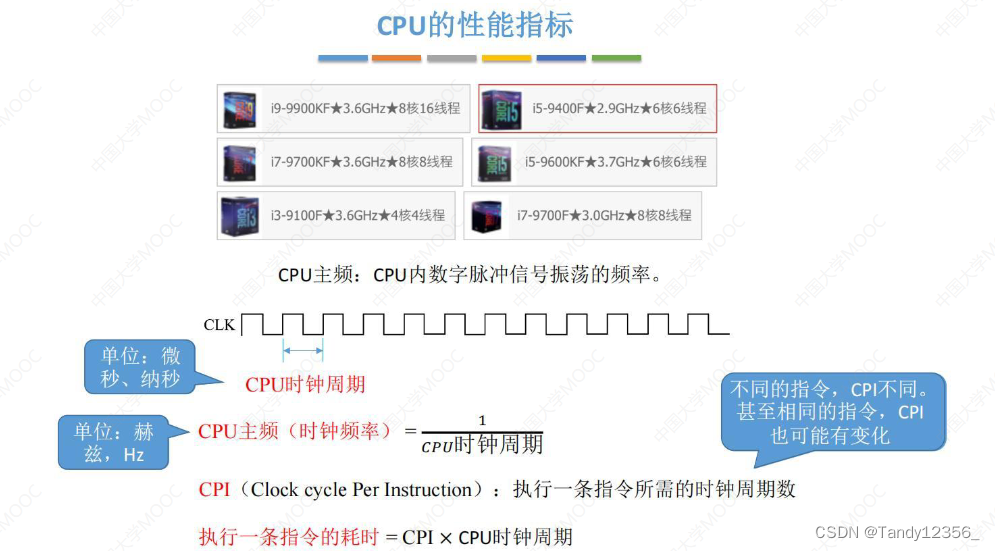
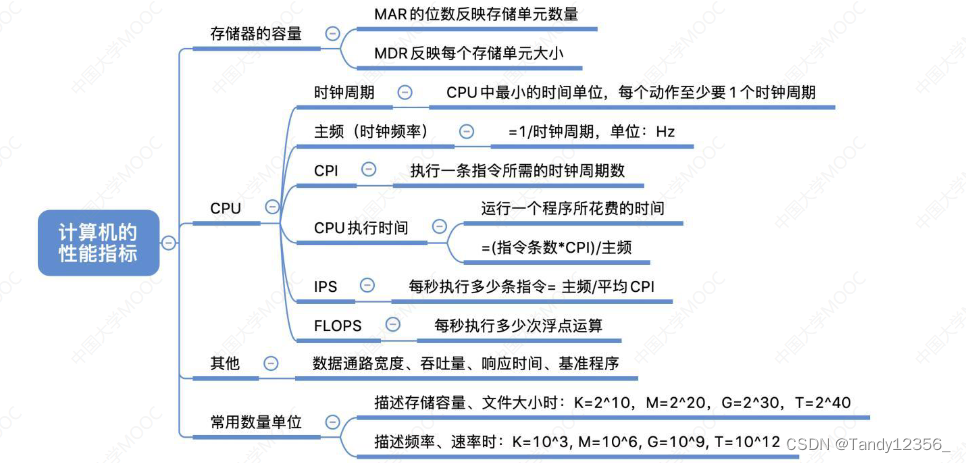
计算机的性能指标
存储器总容量=mar位数*mdr位数
乘法指令比加法指令的步骤要多
吞吐量：单位时间内处理请求的数量
CPI：执行一条指令所需的时钟周期
相关文章：
王道考研计算机组成原理——计算机硬件的基础知识
计算机组成原理的基本概念 计算机硬件的针脚都是用来传递信息，传递数据用的： 服务程序包含一些调试程序： 计算机硬件的基本组成 控制器通过电信号来协调其他部件的工作，同时负责解析存储器里存放的程序指令，然后指挥…...
[晕事]今天做了件晕事21；设置代理访问网站的时候需注意的问题
今天在家上班，设置好VPN，通过代理来访问公司内部的一个系统浏览器的反应如下： Hmmm… can’t reach this page ***.com refused to connect. 这个返回的错误，非常的具有迷惑性，提示的意思：拒绝链接…...
Go通过reflect.Value修改值
到目前为止，反射还只是程序中变量的另一种读取方式。然而，在本节中我们将重点讨论如何通过反射机制来修改变量。 回想一下，Go语言中类似x、x.f[1]和*p形式的表达式都可以表示变量，但是其它如x 1和f(2)则不是变量。一个变量就是一…...
【MySql】4- 实践篇(二)
文章目录 1. SQL 语句为什么变“慢”了1.1 什么情况会引发数据库的 flush 过程呢？1.2 四种情况性能分析1.3 InnoDB 刷脏页的控制策略 2. 数据库表的空间回收2.1 innodb_file_per_table参数2.2 数据删除流程2.3 重建表2.4 Online 和 inplace 3. count(*) 语句怎样实现…...
获取多个接口的数据并进行处理，使用Promise.all来等待所有接口请求完成
Promise.all (等待机制) 方法 它调用了多个函数，这些函数返回了Promise对象，每个Promise对象代表了一个异步操作。 然后，使用Promise.all将这多个Promise对象包装成一个新的Promise对象，它会等待所有的Promise都完成（或…...
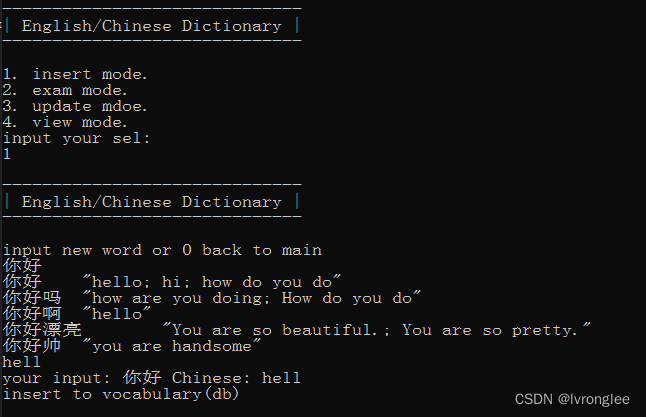
利用C++开发一个迷你的英文单词录入和测试小程序-升级版本
我们现在有了一个本地sqlite3的迷你英文单词小测试工具，需求就跟工作当中一样是不断变更的。这里虚构两个场景，并且一步一步的完成最终升级后的小demo。 场景：数据不依赖本地sqlite3，需要支持远程访问，用目前的restfu…...
实现手撸神经网络230902)
用c动态数组(实现权重矩阵可视化)实现手撸神经网络230902
变量即内存、指针使用的架构原理： 1、用结构struct记录 网络架构，如 float*** ws 为权重矩阵的指针（指针地址）； 2、用 = (float*)malloc (Num * sizeof(float)) 给 具体变量分配内存； 3、用 = (float**)malloc( Num* sizeof(float*) ) 给 指向 具体变量（一维数组）的…...
Android.mk和Android.bp
公司承接Android、iOS等APP开发、前后端网站开发、小程序开发、安全服务等项目！ 公司官网:www.bincodesec.com 项目案例 一、编译不同类型的模块 1.编译成Java库 Android.mk include $(BUILD_JAVA_LIBRARY)Android.bp java_library {} 2.编译成Java静态库 And…...
CSS 常用样式-文本属性
一、水平对齐 text-align CSS中的text-align属性用于水平对齐文本。它可以应用于块级元素和表格单元格。 常见的属性值包括： left：左对齐，文本在容器的左侧。right：右对齐，文本在容器的右侧。center：居中…...
BootstrapBlazor企业级组件库：前端开发的革新之路
作为一名Web开发人员，开发前端我们一般都是使用JavaScript，而Blazor就是微软推出的基于.Net平台交互式客户Web UI 框架，可以使用C#替代JavaScript，减少我们的技术栈、降低学习前端的成本。 而采用Blazor开发，少不了需…...
力扣 -- 1745. 分割回文串 IV
解题步骤： 参考代码： class Solution { public:bool checkPartitioning(string s) {int ns.size();vector<vector<bool>> dp(n,vector<bool>(n));for(int in-1;i>0;i--){for(int ji;j<n;j){if(s[i]s[j]){dp[i][j]i1<j?dp[i…...
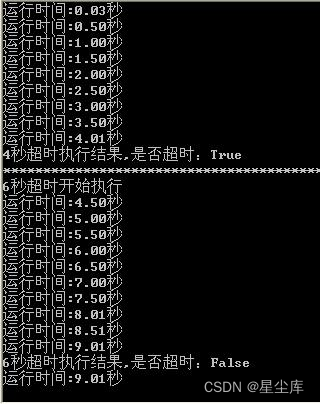
C# 给某个方法设定执行超时时间
C# 给某个方法设定执行超时时间在某些情况下(例如通过网络访问数据)，常常不希望程序卡住而占用太多时间以至于造成界面假死。 在这时、我们可以通过Thread、Thread Invoke（UI）或者是 delegate.BeginInvoke 来避免界面假死， 但是…...
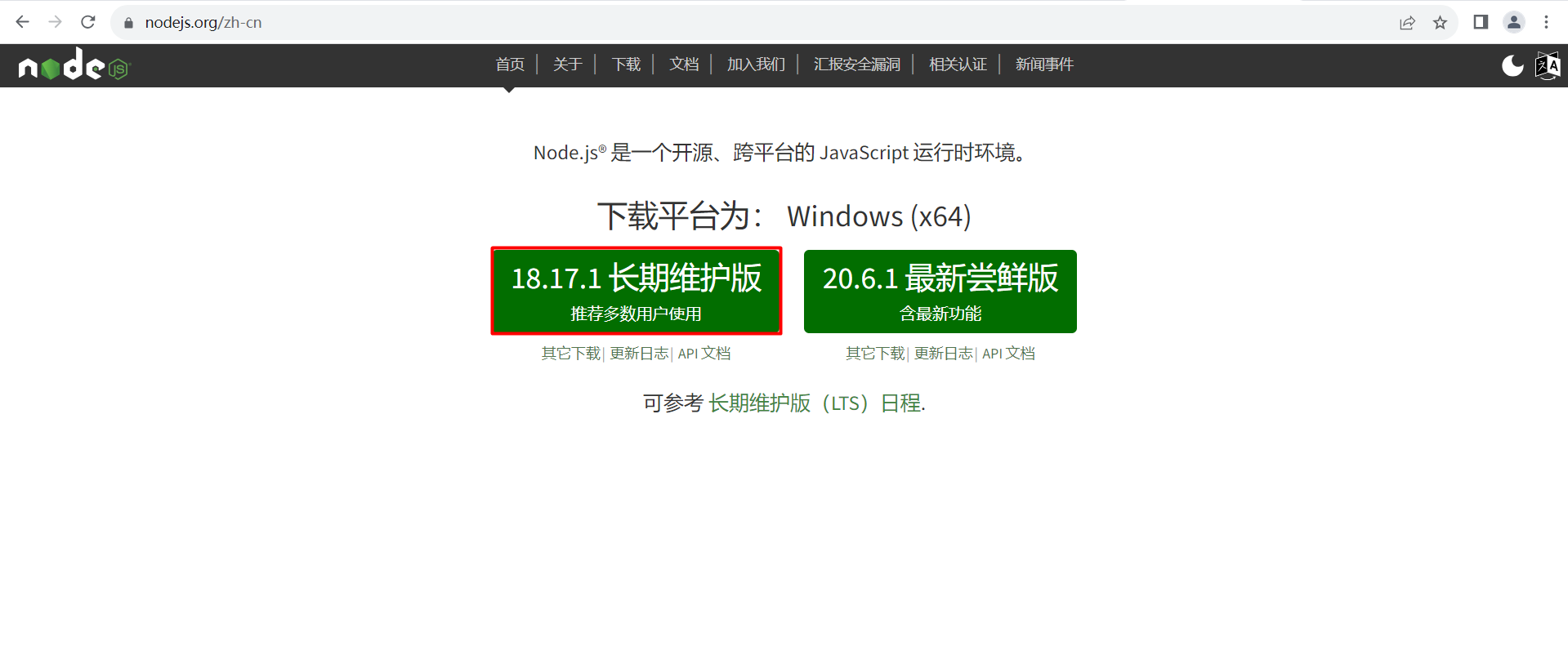
安装NodeJS并使用yarn下载前端依赖
文章目录 1、安装NodeJS1.1 下载NodeJS安装包1.2 解压并配置NodeJS1.3 验证是否安装成功2、使用yarn下载前端依赖2.1 安装yarn2.2 使用yarn下载前端依赖参考目标：在Windows下安装新版NodeJS，并使用yarn下载前端依赖，实现运行前端项目。 1、安装NodeJS 1.1 下载NodeJS安装包…...
（Java高级教程）第三章Java网络编程-第八节：博客系统搭建（前后端分离）
文章目录 一：前端页面回顾二：博客功能展示三：数据库表设计（1）表设计（2）封装DataSource 四：实体类和数据访问对象（1）实体类（2）数据访问…...
901. 股票价格跨度
设计一个算法收集某些股票的每日报价，并返回该股票当日价格的 跨度 。 当日股票价格的 跨度 被定义为股票价格小于或等于今天价格的最大连续日数（从今天开始往回数，包括今天）。 例如，如果未来 7 天股票的价格是 [100,…...
JavaScript中的模块化编程，包括CommonJS和ES6模块的区别。
聚沙成塔每天进步一点点 ⭐ 专栏简介⭐ 模块化编程概述⭐ CommonJS 模块⭐ ES6 模块⭐ 区别⭐ 写在最后 ⭐ 专栏简介 前端入门之旅：探索Web开发的奇妙世界 欢迎来到前端入门之旅！感兴趣的可以订阅本专栏哦！这个专栏是为那些对Web开发感兴趣、…...
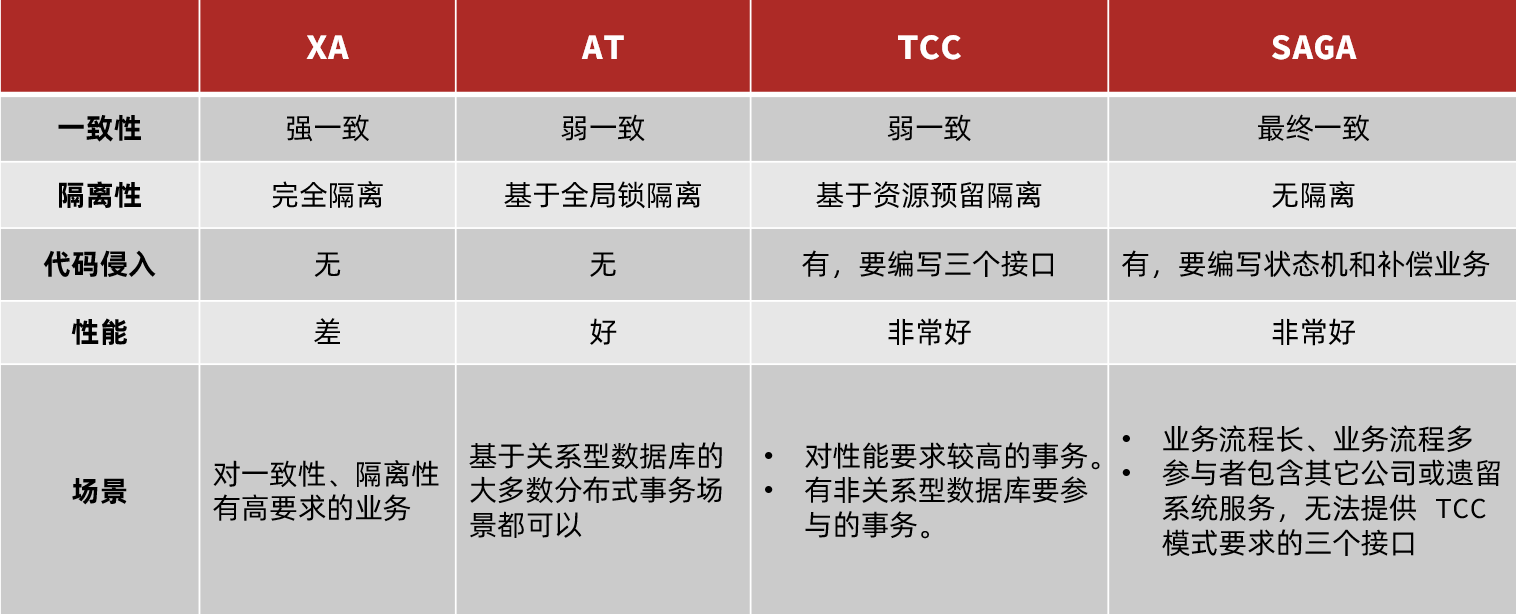
从零开始 Spring Cloud 13：分布式事务
从零开始 Spring Cloud 13：分布式事务 1.分布式事务问题 用一个示例项目演示在分布式系统中使用事务会产生的问题。 示例项目的 SQL：seata_demo.sql 示例项目代码：seata-demo.zip 这个示例项目中的微服务的互相调用依赖于 Nacos…...
2023Node.js零基础教程(小白友好型)，nodejs新手到高手，（二）NodeJS入门——buffer模块、计算机基础、fs模块、path模块
就算步子乱了又如何，接着跳下去就好了。——《闻香识女人》 开始 011_Buffer_介绍与创建 hello，大家好，我们来学习一下buffer。首先来看看 buffer 是一个什么东东。buffer，中文译为缓冲区，是一个类似于数组的对象&am…...
lua如何调用C/C++
1 lua vs C/C lua是脚本语言，优点是门槛低，可以热更新，缺点当然就是性能。C/C是编译型语言，有点是性能高，但是相对的，门槛高，技术不好的人写的代码可能还没有lua的性能高，容易出现c…...
简单聊一聊公平锁和非公平锁，parallel并行流
目录 一、降低锁的粒度，将synchronized关键字不放在方法上了，改为synchronized代码块。二、先区分一下公平锁和非公平锁1、公平锁2、非公平锁3、公平锁的优缺点：4、非公平锁的优缺点： 三、是否对症下药四、IntStream.rangeClosed是…...
手游刚开服就被攻击怎么办？如何防御DDoS？
开服初期是手游最脆弱的阶段，极易成为DDoS攻击的目标。一旦遭遇攻击，可能导致服务器瘫痪、玩家流失，甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案，帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...
调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候，遇到了一些问题，记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...
云计算——弹性云计算器（ECS）
弹性云服务器：ECS 概述 云计算重构了ICT系统，云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台，包含如下主要概念。 ECS（Elastic Cloud Server）：即弹性云服务器，是云计算…...
.Net框架，除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...
iPhone密码忘记了办？iPhoneUnlocker，iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候，难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵，或者买了二手 iPhone 却被原来的 iCloud 账号锁住，这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...
YSYX学习记录（八）
C语言，练习0： 先创建一个文件夹，我用的是物理机： 安装build-essential 练习1： 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件，随机修改或删除一部分，之后…...
HTML 列表、表格、表单
1 列表标签 作用：布局内容排列整齐的区域 列表分类：无序列表、有序列表、定义列表。 例如： 1.1 无序列表 标签：ul 嵌套 li，ul是无序列表，li是列表条目。 注意事项： ul 标签里面只能包裹 li…...
linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行，YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID： YW3…...
Spring Boot+Neo4j知识图谱实战：3步搭建智能关系网络！
一、引言 在数据驱动的背景下，知识图谱凭借其高效的信息组织能力，正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合，探讨知识图谱开发的实现细节，帮助读者掌握该技术栈在实际项目中的落地方法。 …...
Map相关知识
数据结构 二叉树 二叉树，顾名思义，每个节点最多有两个“叉”，也就是两个子节点，分别是左子 节点和右子节点。不过，二叉树并不要求每个节点都有两个子节点，有的节点只 有左子节点，有的节点只有…...