蓝桥杯每日一题2023.10.7
跑步锻炼 - 蓝桥云课 (lanqiao.cn)
题目描述

题目分析
简单枚举,对于+2的情况特判即可
#include<bits/stdc++.h>
using namespace std;
int num, ans, flag;
int m[13] = {0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
bool is_ren(int n)
{if((n % 4 == 0 && n % 100 != 0) || n % 400 == 0)return true;return false;
}
int main()
{for(int i = 2000; i <= 2020; i ++){if(is_ren(i))m[2] = 29;else m[2] = 28;for(int j = 1; j <= 12; j ++){for(int k = 1; k <= m[j]; k ++){num ++;if(k == 1 || (num % 7 - 3) == 0)ans += 2;else ans += 1; if(i == 2020 && j == 10 && k == 1){flag = 1;break;}}if(flag)break;}if(flag)break;}cout << ans;return 0;
}相关文章:

蓝桥杯每日一题2023.10.7
跑步锻炼 - 蓝桥云课 (lanqiao.cn) 题目描述 题目分析 简单枚举,对于2的情况特判即可 #include<bits/stdc.h> using namespace std; int num, ans, flag; int m[13] {0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31}; bool is_ren(int n) {if((n %…...
Linux 系统为何产生大量的 core 文件?
Author:rab 目录 一、问题分析二、解决方案扩展 一、问题分析 上一篇刚讲到《Docker 配置基础优化》,这里再补充一下。就在中秋国庆这段小长假里,接收到了线上服务器磁盘告警通知,线上服务器架构是一个 Docker Swarm 集群&#x…...
Web_python_template_injection SSTI printer方法
这题挺简单的 就是记录一下不同方法的rce python_template_injection ssti了 {{.__class__.__mro__[2].__subclasses__()}} 然后用脚本跑可以知道是 71 {{.__class__.__mro__[2].__subclasses__()[71]}} 然后直接 init {{.__class__.__mro__[2].__subclasses__()[71].__i…...
)
TCP/IP网络江湖——江湖导航(网络层上篇)
目录 一、引言 二、IP地址与路由 三、IP协议与数据包转发 3.1 IP协议:网络江湖的规矩...
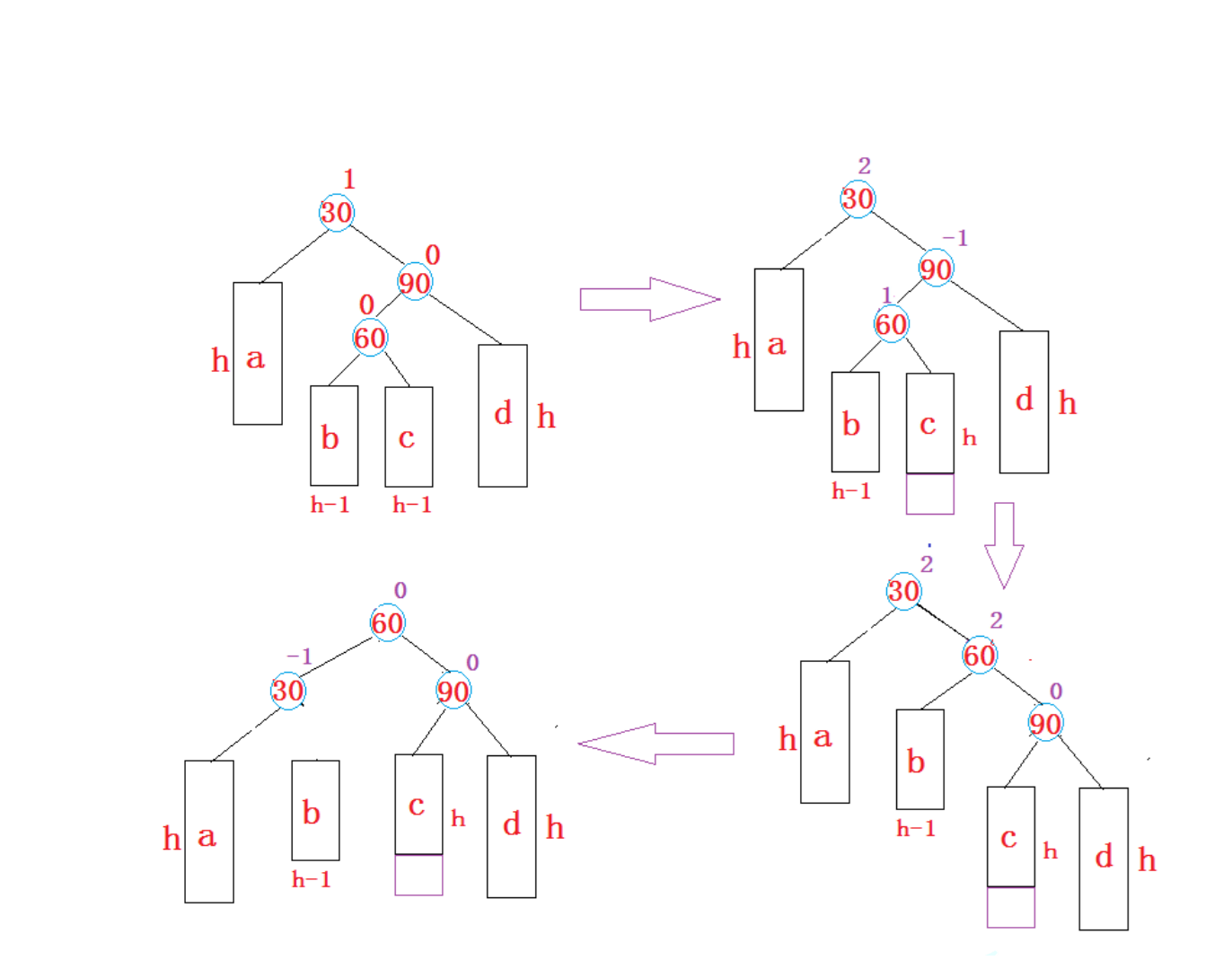
数据结构——AVL树(详解 + C++模拟实现)
文章目录 前言AVL树的概念AVL树节点的定义AVL树类框架AVL树的插入AVL树的旋转新节点插入较高子树的左侧 —— 左左: 右单旋新节点插入较高右子树的右侧——右右: 左单旋新节点插入较高左子树的右侧 —— 左右: 先左单旋然后再有单旋新节点插入较高右子树的左侧&…...

redis 雪崩,穿透,击穿及解决方案
一、缓存雪崩: 1. 原因: 缓存雪崩是指在我们设置缓存时大量采用了相同的过期时间,导致缓存在某一时刻同时失效,请求全部转发到DB,DB瞬时压力过重雪崩。 2. 解决方案: 将失效时间分散,通过生成随机数使得key的过期时间…...
Flutter环境搭建及新建项目
一、下载安装压缩包 https://storage.flutter-io.cn/flutter_infra_release/releases/stable/windows/flutter_windows_3.10.6-stable.zip 二、解压缩 解压之后,将里面的flutter整体拿出来 三、配置环境变量 将flutter/bin全路径配置到系统环境变量里面 四、运行…...

【面试题精讲】深拷贝和浅拷贝区别了解吗?什么是引用拷贝?
“ 有的时候博客内容会有变动,首发博客是最新的,其他博客地址可能会未同步,认准https://blog.zysicyj.top ” 首发博客地址[1] 面试题手册[2] 系列文章地址[3] 深拷贝和浅拷贝的区别: 深拷贝(Deep Copy)和浅拷贝&#…...

CentOS7.9中使用packstack安装train版本
这里写目录标题 材料准备为什么选择packstack安装静态ip系统配置使用阿里云yum源安装packstack部署openstack 材料准备 ecs云服务器8核心16g内存一台,系统盘100GB,系统CentOS7.9vpc网段:192.168.0.1/24eip一个,带宽5M以上 为什么…...

mfw git泄露构造闭合
这题也挺有想法 第一次确实没有想到 首先我们可以扫出 git 然后 我们githack 泄露一下 然后我们看index.php代码 <?phpif (isset($_GET[page])) {$page $_GET[page]; } else {$page "home"; }$file "templates/" . $page . ".php";/…...
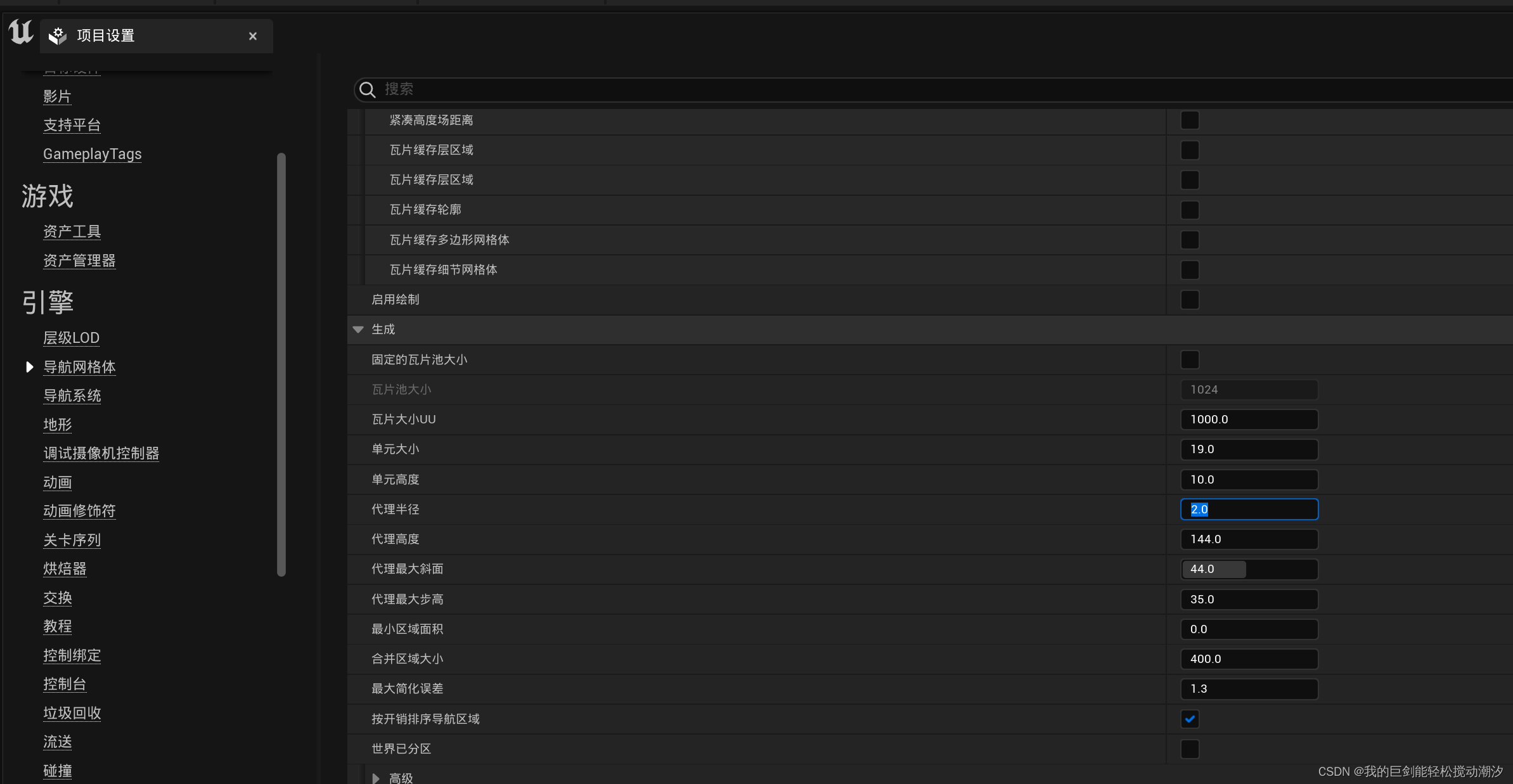
UE5修改导航网格的参数
Unreal Engine 4 - Recast NavMesh Size, how to Change Agent Radius / Tutorial - YouTubehttps://www.youtube.com/watch?vf3hF6xdmCTk 修改当前的 代理半径就是一般贴边的长度 修改编辑器的...
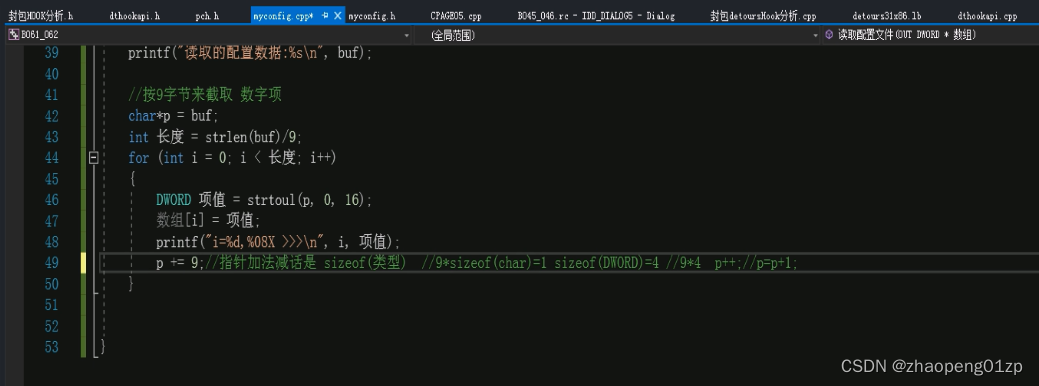
郁金香2021年游戏辅助技术中级班(七)
郁金香2021年游戏辅助技术中级班(七) 058-C,C写代码HOOK分析封包数据格式A059-C,C写代码HOOK分析封包数据格式B-detours劫持060-C,C写代码HOOK分析封包数据格式C-过滤和格式化061-C,C写代码HOOK分析封包数据格式D-写入配置文件062-C,C写代码HOOK分析封包…...
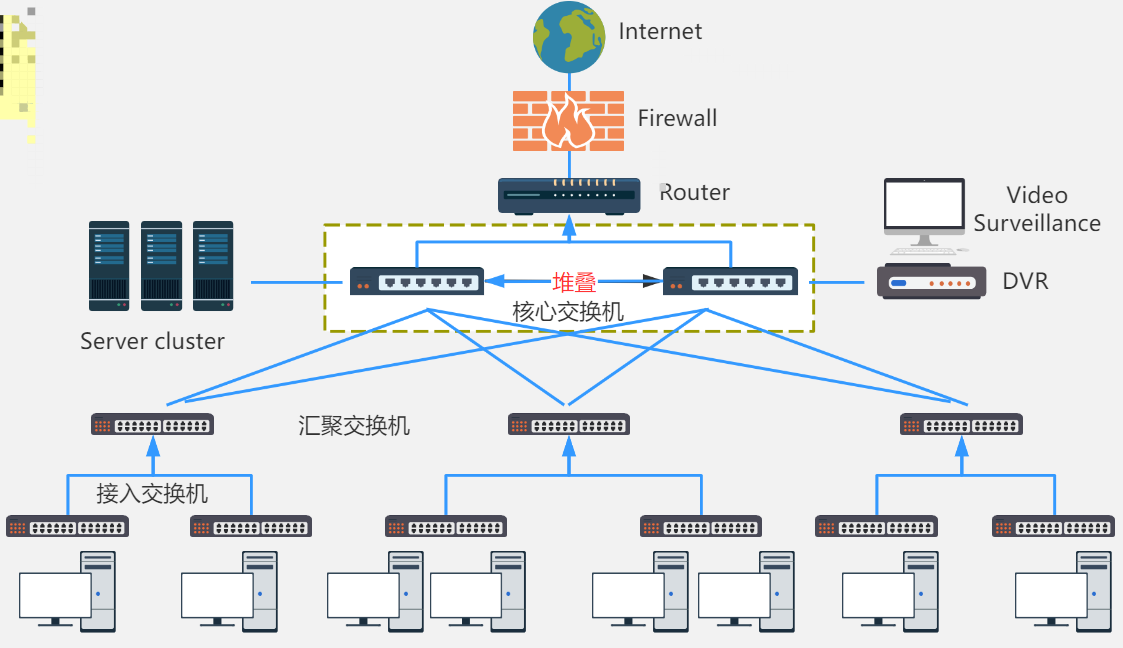
【网络】路由器和交换机的区别
🍁 博主 "开着拖拉机回家"带您 Go to New World.✨🍁 🦄 个人主页——🎐开着拖拉机回家_Linux,大数据运维-CSDN博客 🎐✨🍁 🪁🍁 希望本文能够给您带来一定的帮助…...
 函数、COALESCE()函数、DATEDIFF()函数)
SQL的CASE WHEN函数、CAST函数、CONVERT() 函数、COALESCE()函数、DATEDIFF()函数
一、CASE WHEN简单使用 SELECT CASE WHEN age > 18 AND age < 25 THEN 18-25WHEN age > 25 AND age < 35 THEN 25-35WHEN age > 35 AND age < 45 THEN 36-45ELSE 45END AS age_groupFROM peopleGROUP BY age_group;二、CASE WHEN语句与聚合函数一起使用 SE…...
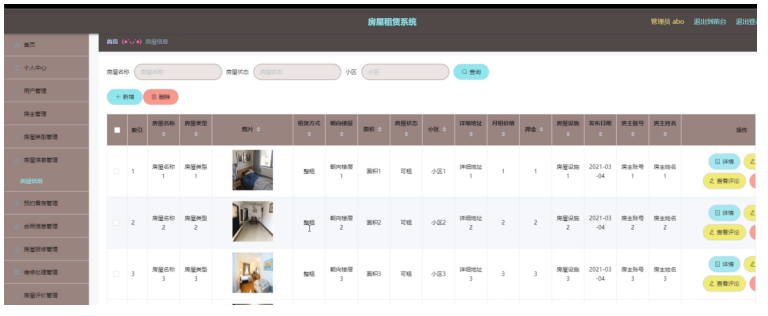
前后端分离计算机毕设项目之基于springboot+vue的房屋租赁系统《内含源码+文档+部署教程》
博主介绍:✌全网粉丝10W,前互联网大厂软件研发、集结硕博英豪成立工作室。专注于计算机相关专业毕业设计项目实战6年之久,选择我们就是选择放心、选择安心毕业✌ 🍅由于篇幅限制,想要获取完整文章或者源码,或者代做&am…...

《Spring框架前世今生》
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🦄 博客首页——🐅🐾猫头虎的博客🎐 🐳 《面试题大全专栏》 🦕 文章图文…...

基于树种优化的BP神经网络(分类应用) - 附代码
基于树种优化的BP神经网络(分类应用) - 附代码 文章目录 基于树种优化的BP神经网络(分类应用) - 附代码1.鸢尾花iris数据介绍2.数据集整理3.树种优化BP神经网络3.1 BP神经网络参数设置3.2 树种算法应用 4.测试结果:5.M…...

纳百川冲刺创业板上市:计划募资约8亿元,宁德时代为主要合作方
近日,纳百川新能源股份有限公司(下称“纳百川”)向深交所创业板递交的上市申请材料获得受理,浙商证券为其独家保荐人。 本次冲刺上市,纳百川计划募资8.29亿元,将用于纳百川(滁州)新能…...

light client轻节点简介
1. 引言 前序博客: Helios——a16z crypto构建的去中心化以太坊轻节点 去中心化和自我主权对于Web3的未来至关重要,但是这些理想并不总适用于每个项目或应用程序。在非托管钱包和bridges等工具中严格优先考虑安全性而不是便利性的用户,可选…...

1500*B. Zero Array(贪心数学找规律)
Problem - 1201B - Codeforces 解析: 因为每次减少2,如果总和为奇数肯定无法实现。 特例,如果某个数大于其他所有数的总和,同样无法实现。 其他均可实现。 #include<bits/stdc.h> using namespace std; #define int long l…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...

力扣热题100 k个一组反转链表题解
题目: 代码: func reverseKGroup(head *ListNode, k int) *ListNode {cur : headfor i : 0; i < k; i {if cur nil {return head}cur cur.Next}newHead : reverse(head, cur)head.Next reverseKGroup(cur, k)return newHead }func reverse(start, end *ListNode) *ListN…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...

手机平板能效生态设计指令EU 2023/1670标准解读
手机平板能效生态设计指令EU 2023/1670标准解读 以下是针对欧盟《手机和平板电脑生态设计法规》(EU) 2023/1670 的核心解读,综合法规核心要求、最新修正及企业合规要点: 一、法规背景与目标 生效与强制时间 发布于2023年8月31日(OJ公报&…...

通过MicroSip配置自己的freeswitch服务器进行调试记录
之前用docker安装的freeswitch的,启动是正常的, 但用下面的Microsip连接不上 主要原因有可能一下几个 1、通过下面命令可以看 [rootlocalhost default]# docker exec -it freeswitch fs_cli -x "sofia status profile internal"Name …...
