数据结构-----平衡二叉树
目录
前言
1.平衡二叉树
1.1概念与特点
1.2与二叉排序树比较
1.3判断平衡二叉树
2.平衡二叉树的构建
2.1平衡因子 BF
2.2 LL型失衡(右旋)
2.3 RR型失衡(左旋)
2.4 LR型失衡(先左旋再右旋)
2.5 RL型失衡(先右旋再左旋)
2.6构建平衡二叉树代码实现
3.删除节点操作
3.1删除叶子节点
3.2删除只有一个左(右)子树的节点
3.3删除有左右子树的节点
3.4删除节点代码实现
4.平衡二叉树相关操作
4.1查找数据
4.2判断是否为平衡二叉树
4.3中序遍历输出
4.4销毁平衡二叉树
前言
前面我发布了一篇介绍二叉排序树的相关文章,那么今天我们学习一种新的树----平衡二叉树,在此之前我们要学习过二叉排序树,才能更好的去学习平衡二叉树,平衡二叉树是二叉排序树的进一步优化,下面就一起来看看吧!
1.平衡二叉树
1.1概念与特点
在计算机科学中,AVL树是最先发明的自平衡二叉查找树。在AVL树中任何节点的两个子树的高度最大差别为1,所以它也被称为高度平衡树。增加和删除可能需要通过一次或多次树旋转来重新平衡这个树。AVL树得名于它的发明者G. M. Adelson-Velsky和E. M. Landis,他们在1962年的论文《An algorithm for the organization of information》中发表了它。
二叉排序树相关链接:数据结构-----二叉排序树_Gretel Tade的博客-CSDN博客
特性:
- 平衡二叉树是一个二叉排序树
- 它的左子树和右子树都是平衡二叉树
- 左右子树高度之差(简称平衡因子)的绝对值不超过 1(即:-1,0,1)
如图所示: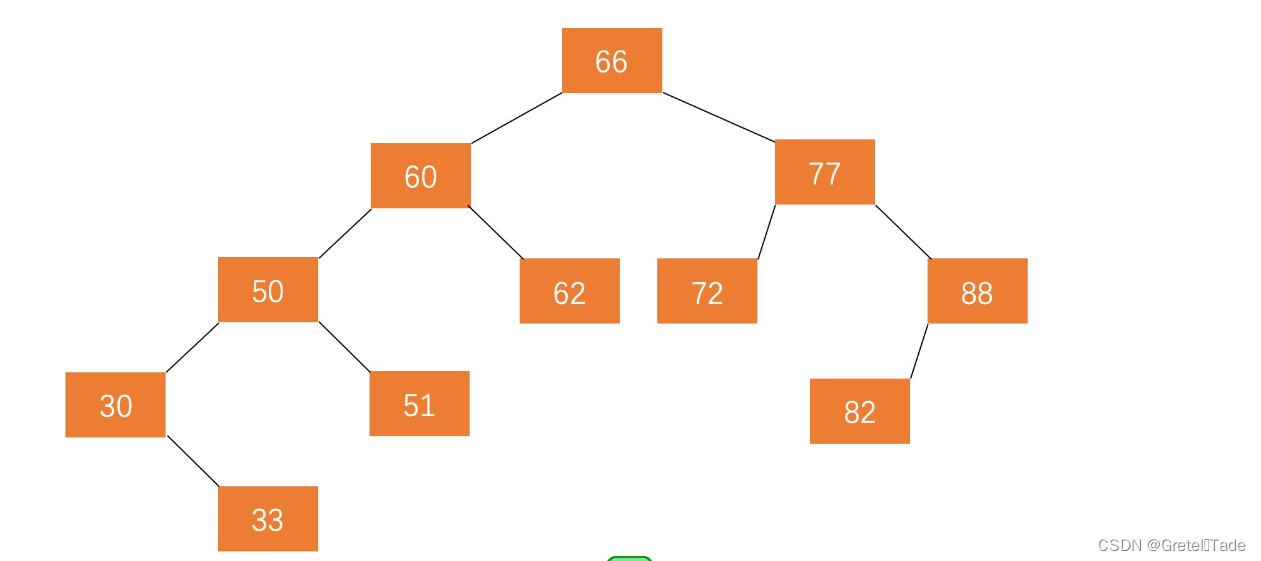
1.2与二叉排序树比较
在此之前我们学习过了二叉排序树的相关知识点,二叉排序树又名为二叉搜索树,但是当一个二叉排序树的形态是一个链状的话,那么搜索效率跟一个链表的搜索效率是毫无区别的,但是如果是一个平衡二叉树就不同了,因为平衡二叉树规定了左右子树高度差不会大于1,这样就可以大大提高了搜索的效率,下面看比较:

当前我插入[1,2,3,4,5,6] 这一数组构建一个二叉排序树的时候,其形态是如下图所示,很明显是一个链态的,无异于一个链表,当我要去搜索数字6的时候,就要遍历到最后一个数字,搜索效率为 O(n)。

但是如果我通过构建平衡二叉树来储存这些数据的话,那就会有很大的不同,如下图所示,当我要去搜索最后一个节点的时候,就不需要去遍历这么多节点了,可以这么说,平衡二叉树是排序二叉树的优化结果。
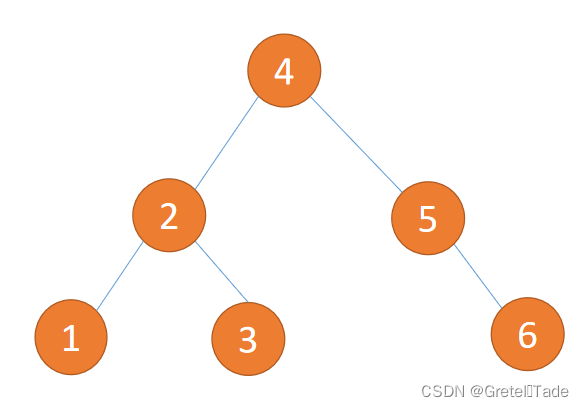
1.3判断平衡二叉树
- 1. 是二叉排序树
- 2. 任何一个节点的左子树或者右子树都是平衡二叉树,而且左右高度差小于等于 1
(1)这个不是平衡二叉树, 因为右子树比左子树高度差大于2

(2)这个不是平衡二叉树,因为没有符合二叉排序树的要求

(3)这个是平衡二叉树,既满足二叉排序树的要求,而且左右子树高度差小于2.
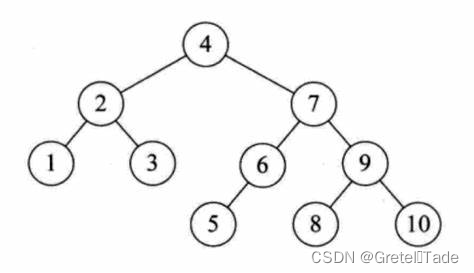
2.平衡二叉树的构建
前面去构建一个二叉排序树,非常简单,只需要排序就行了,那构建一个平衡二叉树不仅仅要考虑到排序问题,还要考虑到左右子树高度不大于1才行,下面我介绍一种通过旋转的方法来去构建平衡二叉树。
2.1平衡因子 BF
定义:左子树和右子树高度差
计算方法:左子树高度减右子树高度的绝对值
当满足BF<=1的时候,这个树就满足平衡条件。当不满足平衡条件的话,那就只能去通过旋转来实现平衡。下面有4种不满足平衡条件的情况,如图所示:
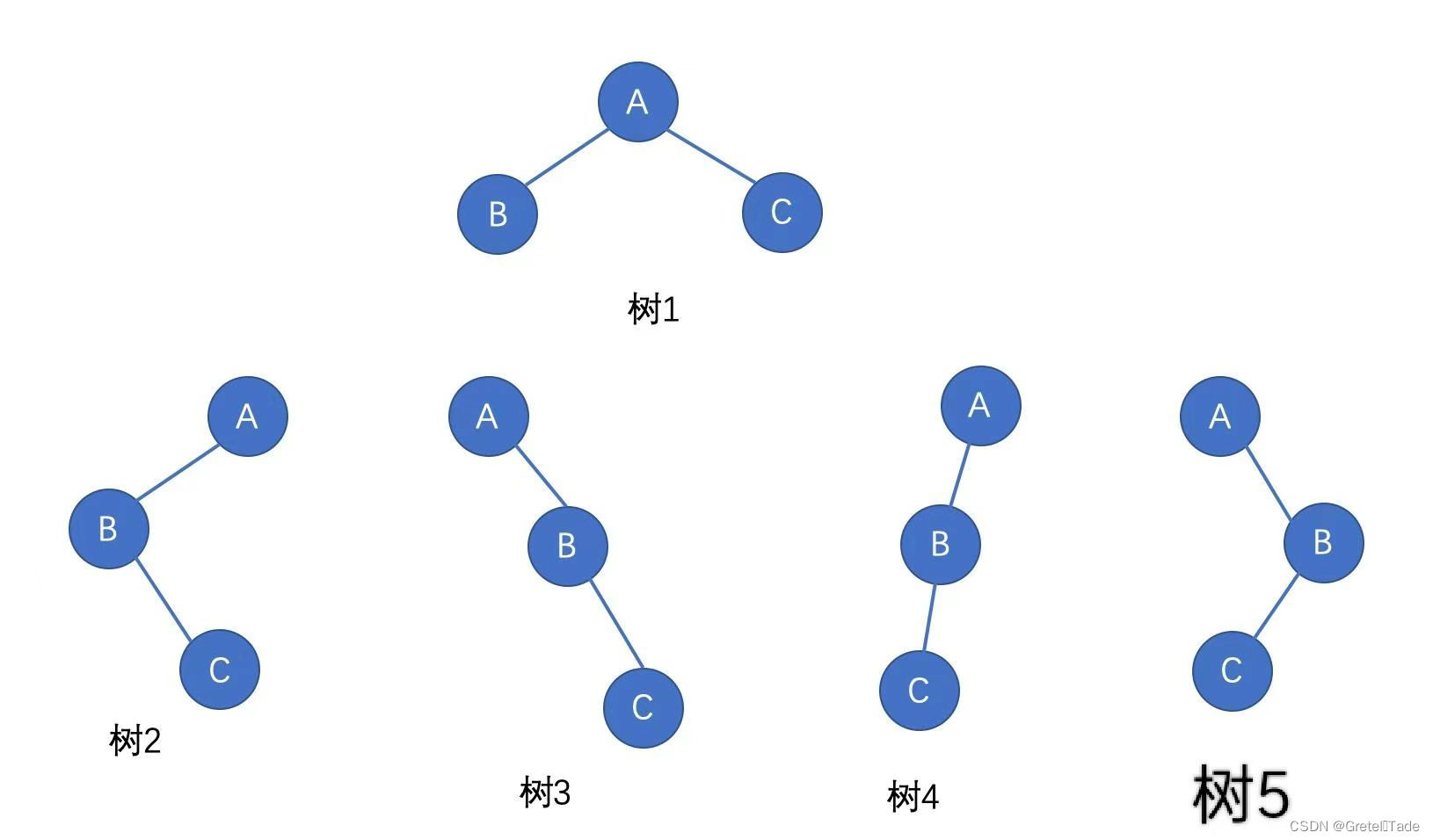
树1是满足平衡条件的情况;
树2是在左子树右子节点出现失衡情况,属于 LR型
树3是在右子树右子节点出现失衡情况,属于 RR型
树4是在左子树左子节点出现失衡情况,属于 LL型
树5是在右子树左子节点出现失衡情况,属于 LR型
下面我就一一讲解怎么去通过旋转来处理上面这四种失衡问题。
2.2 LL型失衡(右旋)
右旋就是通过顺时针旋转来实现平衡,就是处于右边的根结点落下变为叶子节点,而中间的节点变为新的根节点,最左边的叶子节点保持不变,最后形成新的结构。
动图演示: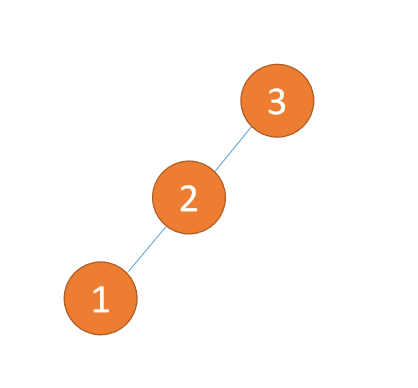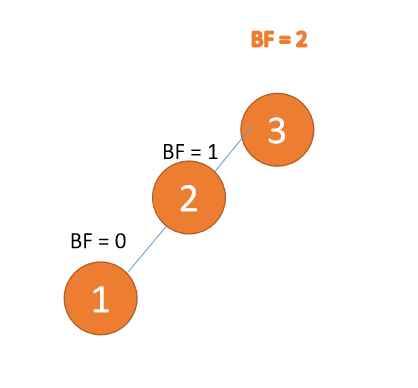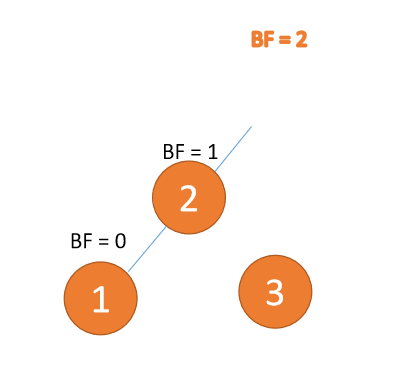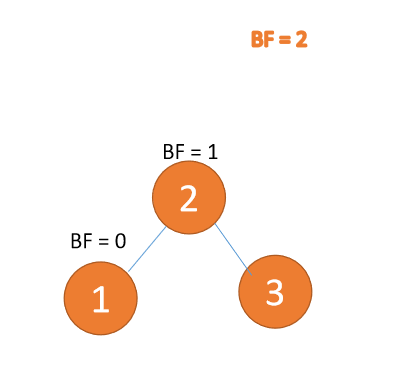
2.3 RR型失衡(左旋)
对于RR型失衡,通过逆时针旋转,最左边的根结点落下,变成叶子节点,中间的节点变为新的根节点,最右边的叶子节点保持不变。
动图演示:
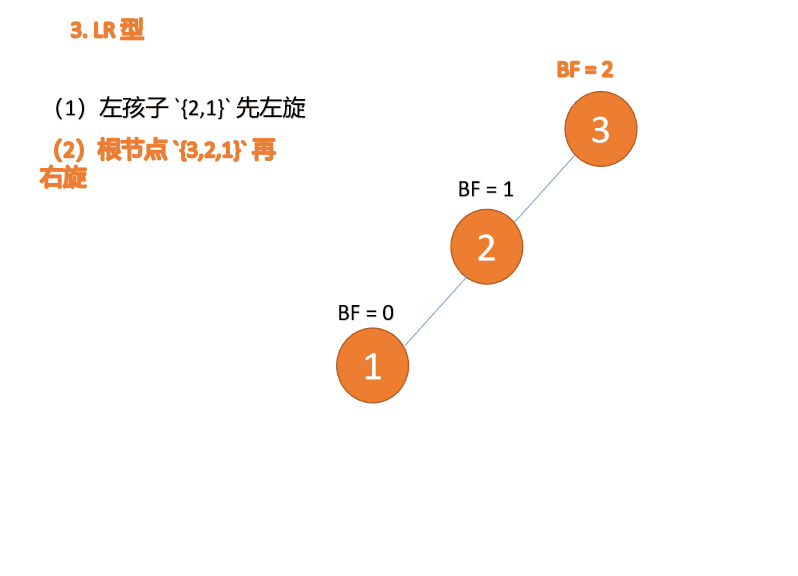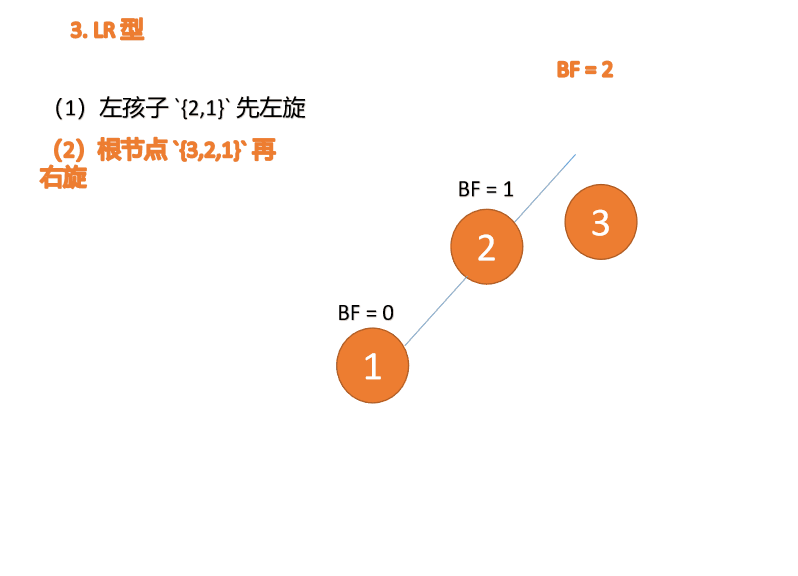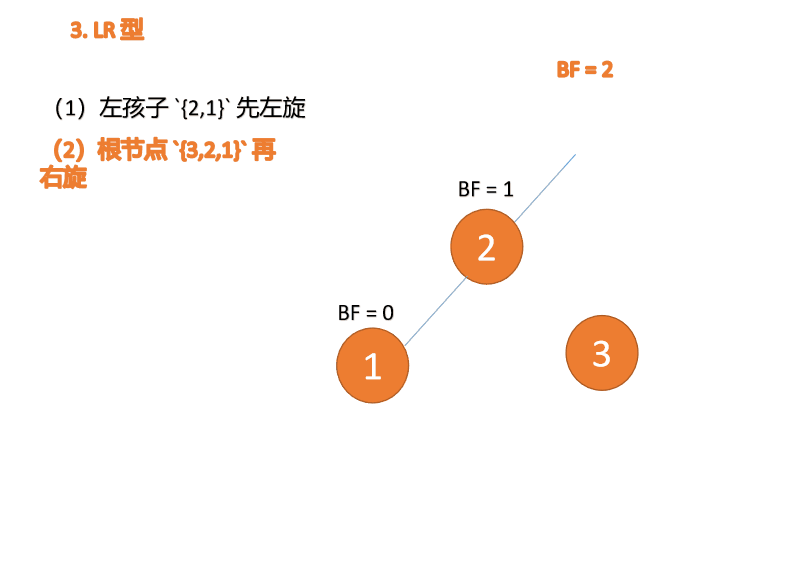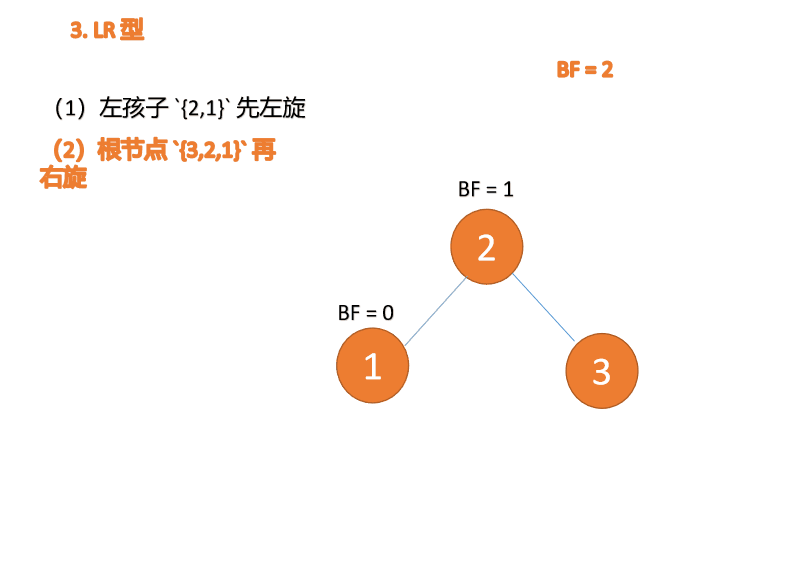
2.4 LR型失衡(先左旋再右旋)
对于LR型失衡,先在根节点左子树进行左旋处理,变成LL型失衡,然后再去通过右旋来实现整体平衡。动图演示如下:
先左旋:

再右旋:
2.5 RL型失衡(先右旋再左旋)
对于RL型失衡,在根节点的右子树先进行右旋处理,形成RR型失衡,然后整体进行左旋处理,最后达到平衡状态,动态演示如下:
先右旋:
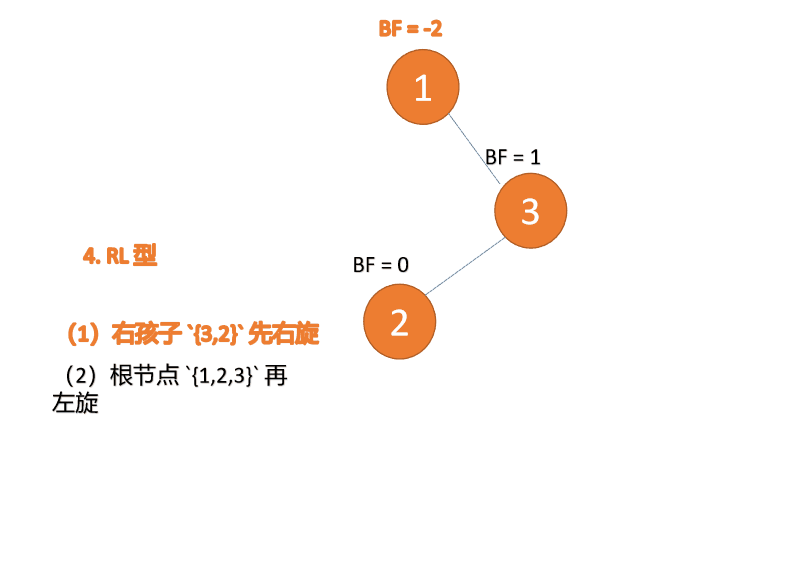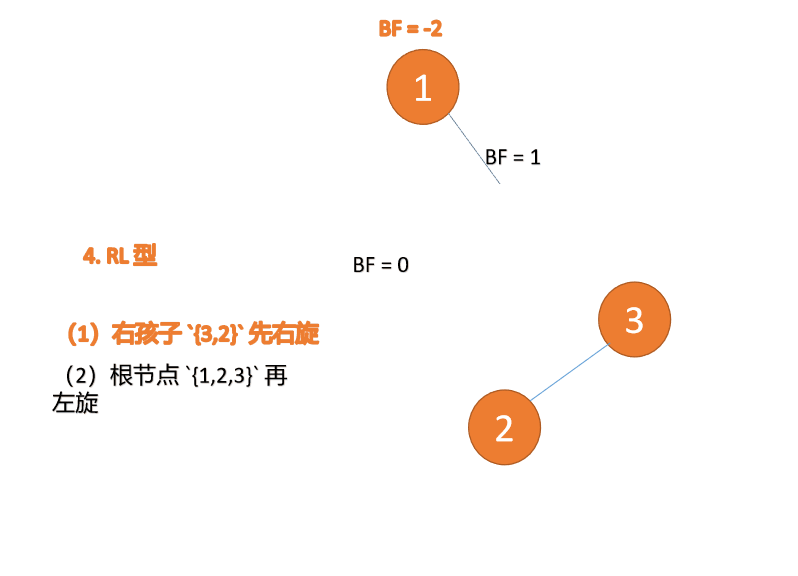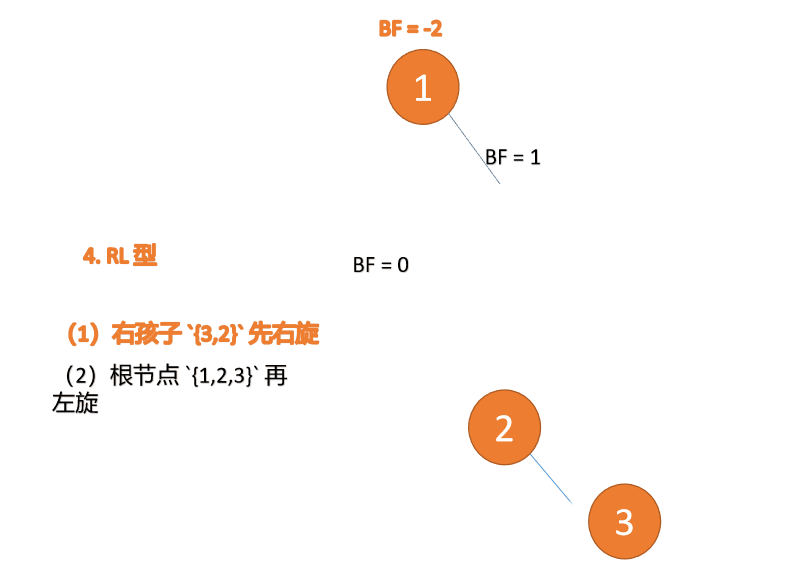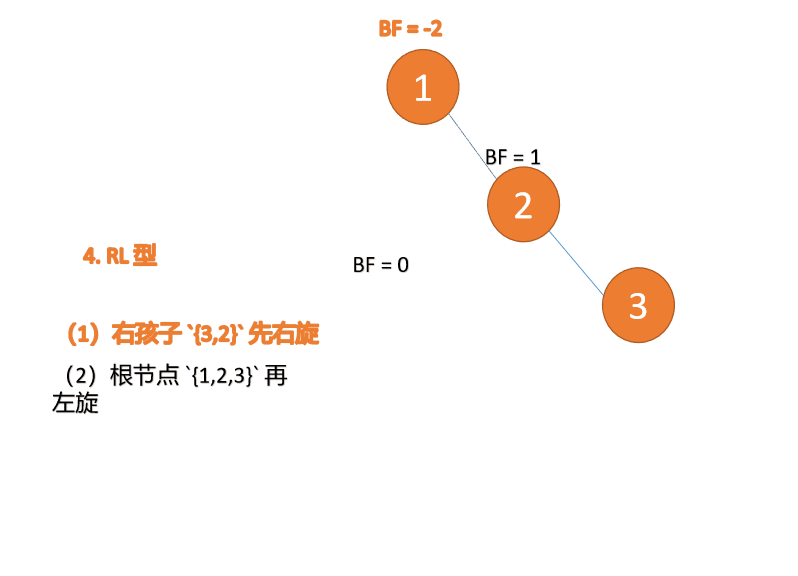 再左旋:
再左旋:
2.6构建平衡二叉树代码实现
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>typedef int Datatype;
typedef struct AVLtree {Datatype data;int heigh;//高度struct AVLtree* left;struct AVLtree* right;
}Node;//绝对值
int abs(int a, int b) {return a - b > 0 ? a - b : b - a;
}//创建一个节点
Node* Create_node(Datatype data) {Node* new_node = (Node*)malloc(sizeof(Node));if (!new_node) {printf("ERROR\n");exit(-1);}new_node->data = data;new_node->left = new_node->right = NULL;new_node->heigh = 0;return new_node;
}//获取高度
int get_height(Node* T) {if (!T)return 0;elsereturn T->heigh;
}//1.插入右子树右节点,右旋
void right_rigth(Node** root) {Node* k = (*root)->right;(*root)->right = k->left;k->left = (*root);k->heigh = get_height(k->left) > get_height(k->right) ? get_height(k->left) : get_height(k->right);(*root)->heigh = get_height((*root)->left) > get_height((*root)->right) ? get_height((*root)->left) : get_height((*root)->right);*root = k;
}
//2.插入左子树左节点,失去平衡,左旋
void left_left(Node** root) {Node* k = (*root)->left;(*root)->left = k->right;k->right = (*root);k->heigh = get_height(k->left) > get_height(k->right) ? get_height(k->left) : get_height(k->right);(*root)->heigh = get_height((*root)->left) > get_height((*root)->right) ? get_height((*root)->left) : get_height((*root)->right);*root = k;
}
//3.插入左子树,右节点,失去平衡,先右旋再左旋
void left_right(Node** root) {right_rigth(&((*root)->left));left_left(&(*root));
}
//4.插入右子树左节点,失去平衡,先左旋再右旋
void rigth_left(Node** root) {left_left(&((*root)->right));right_rigth(&(*root));
}//插入节点
void Insert_node(Datatype data, Node** root) {if (!(*root)) {(*root) = Create_node(data);return;}else {if (data < (*root)->data) {Insert_node(data, &((*root)->left));if (get_height((*root)->left) - get_height((*root)->right) > 1) {//如果出现失衡的情况if(data<(*root)->left->data)left_left(&(*root));elseleft_right(&(*root));}}else if (data > (*root)->data) {Insert_node(data, &((*root)->right));if (get_height((*root)->right) - get_height((*root)->left) > 1) {//如果出现失衡的情况if(data>(*root)->right->data)right_rigth(&(*root));elserigth_left(&(*root));}}else {printf("Do not insert numbers of the same size!\n");return;}}(*root)->heigh++;
}//创建平衡二叉树
void Create_AVLtree(Node** T, Datatype* data,int n) {if (!data) {return;}for (int i = 0; i < n; i++) {Insert_node(data[i],T);}
}3.删除节点操作
在对平衡二叉树进行删除节点的操作时候,跟插入节点也是一样的,会出现失衡的情况,那这里就要通过旋转来去处理了,要进行那种旋转就要根据删除的节点属性去看,以下有4种情况:
- 删除叶子结点
- 删除结点只有左子树
- 删除结点只有右子树
- 删除结点有左、右子树
下面就一个一个来看,怎么去进行删除吧
3.1删除叶子节点
删除叶子节点后要看,平衡二叉树是否失衡,如果没有失衡就直接删除即可;如果出现了失衡的情况就要从根节点开始向上依次检索看从哪个位置开始失衡了,一经发现失衡就进行相对于的旋转处理,直到根结点为止。
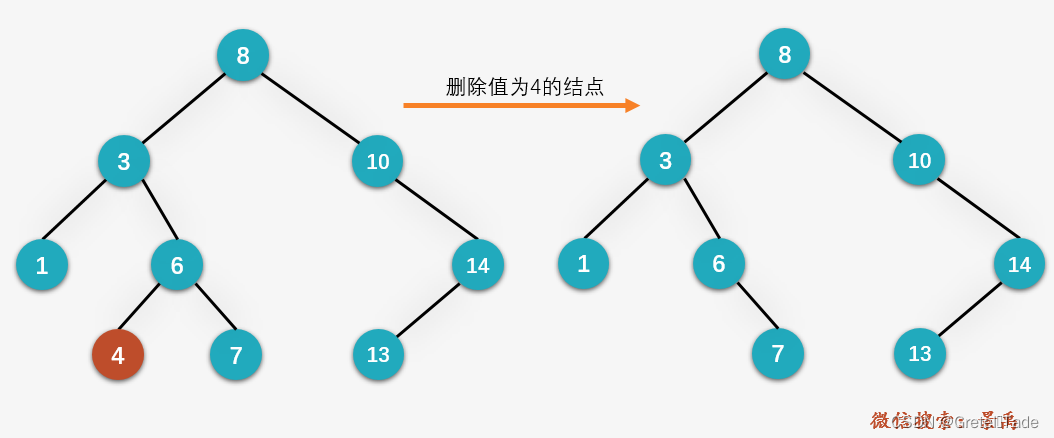
3.2删除只有一个左(右)子树的节点
这种情况就要用这个被删除节点的相邻节点来去顶替这个节点,然后整体进行相对于的旋转操作。如下图所示:

3.3删除有左右子树的节点
要删除的节点有左右子树的话,那么就找到左子树的最大节点或者找到右子树最小节点来替换掉这个节点,然后把这个节点的空间释放掉就行了。
3.4删除节点代码实现
//查找数据节点
Node* Search_node(Node *T,Datatype target) {if (!T) {return NULL;}if (target == T->data)return T;else if (target < T->data)Search_node(T->left, target);elseSearch_node(T->right, target);
}//删除指定数据的节点
void Del_node(Node** T, Datatype target) {Node* dnode = Search_node(*T, target);if (!dnode){//如果查找不成功,就返回printf("bye~~~error\n");return;}if (target < (*T)->data) {Del_node(&(*T)->left, target);if (get_height((*T)->left) - get_height((*T)->right) > 1) {if (target < (*T)->left->data)left_left(&*T);elseleft_right(&*T);}}else if (target > (*T)->data) {Del_node(&(*T)->right, target);if (get_height((*T)->right) - get_height((*T)->left) > 1) {if (target < (*T)->right->data)rigth_left(&*T);elseright_rigth(&*T);}}//此时(*T)就是要删除的节点//1.如果这个节点都有左右子树的话else if ((*T)->left && (*T)->right) {//找到右子树最左边的节点,也就是比这个要删除节点大一位的节点Node* min = (*T)->right;while (min->left)min = min->left;(*T)->data = min->data;Del_node(&(*T)->right, min->data);}//2.如果这个节点有一个左右子树或者没有子树的情况else {Node* dnode = (*T);(*T) = (*T)->left ? (*T)->left : (*T)->right;//把这个节点进行替换掉free(dnode);//释放空间,删除这个节点}//高度重新处理if((*T))(*T)->heigh=get_height((*T)->left)>get_height((*T)->right)? get_height((*T)->left)+1: get_height((*T)->right)+1;
}4.平衡二叉树相关操作
4.1查找数据
查找数据然后返回这个节点,我们直接通过二分查找就行了,代码如下:
//查找数据节点
Node* Search_node(Node *T,Datatype target) {if (!T) {return NULL;}if (target == T->data)return T;else if (target < T->data)Search_node(T->left, target);elseSearch_node(T->right, target);
}4.2判断是否为平衡二叉树
根据平衡二叉树的特性,我们需要判断这个二叉树是否排序,是否满足左右子树高度差不大于1 ,这里就需要用到递归一层一层检索了,最后取和运算,代码如下:
//判断一个树是否为平衡二叉树
bool Judge(Node* T) {if (!T){printf("NULL\n");exit(0);}if(T->left->data>T->data||T->right->data<T->data)return false;if (abs(get_height(T->left) - get_height(T->right)) > 1)return false;elsereturn true;return Judge(T->left)&&Judge(T->right);
}4.3中序遍历输出
//中序遍历输出
void In_travel(Node* T) {if (!T)return;In_travel(T->left);printf("%d ", T->data);In_travel(T->right);
}4.4销毁平衡二叉树
销毁平衡二叉树就要把每一个节点的空间释放掉,那就直接从下往上去释放空间,代码如下:
//销毁
void Destroy(Node** T) {if (!*T)return;Destroy(&(*T)->left);Destroy(&(*T)->right);free(*T);
}以上就是本期的全部内容了,我们下一期再见!
分享一张壁纸: 
相关文章:

数据结构-----平衡二叉树
目录 前言 1.平衡二叉树 1.1概念与特点 1.2与二叉排序树比较 1.3判断平衡二叉树 2.平衡二叉树的构建 2.1平衡因子 BF 2.2 LL型失衡(右旋) 2.3 RR型失衡(左旋) 2.4 LR型失衡(先左旋再右旋) 2.5 RL…...

vue3 keepalive翻页保存页面状态
描述 实现页面 A-> B , B->A(A保存之前页面状态,不刷新页面) // router/index.tsimport { createRouter, createWebHistory } from vue-router import HomeView from ../views/HomeView.vueconst router createRouter({h…...
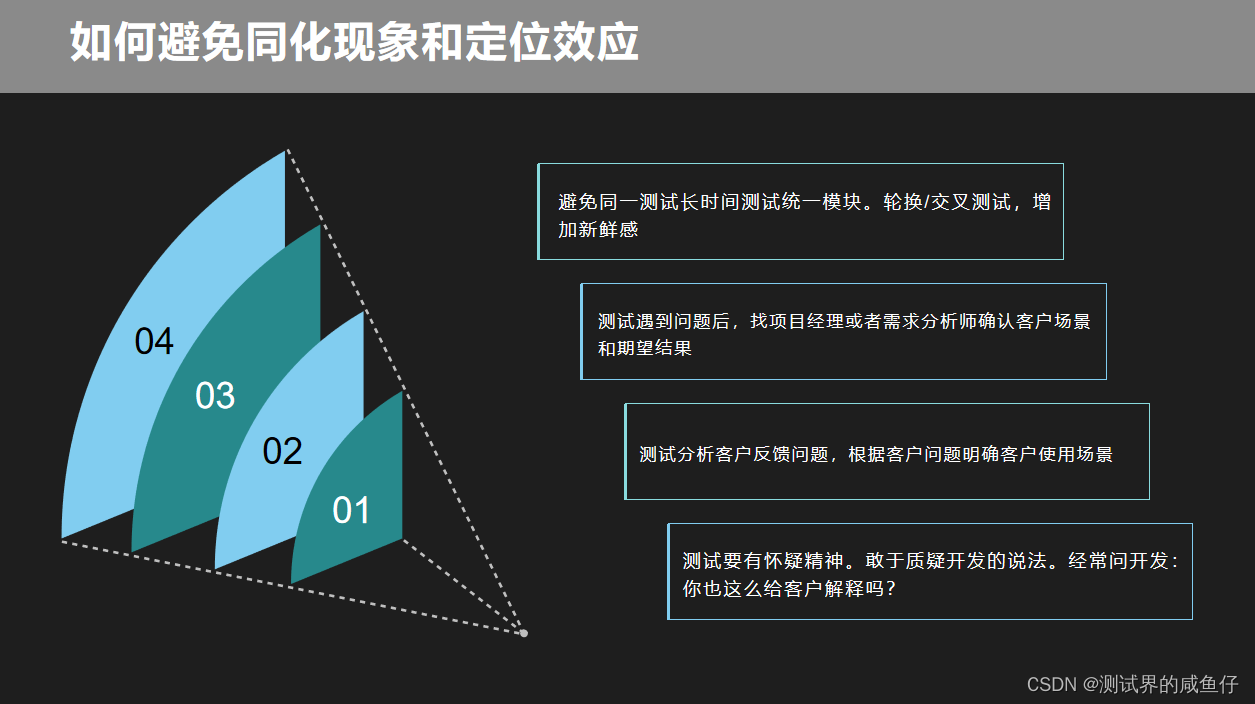
测试工程师思维学习
一、测试工程师应具备什么思维? 透过现象看本质,拒绝“一叶障目” 01、质疑和系统思维 02、创新思维 03、全局思维 04、风险驱动和组合思维 05、用户为中心和比较思维 06、BT思维和架构扩展性思维 二、测试工程师应避免的思维 01、同化现象 02、定位效…...
前端JavaScript入门到精通,javascript核心进阶ES6语法、API、js高级等基础知识和实战 —— Web APIs(六)
思维导图 一、正则表达式 1.1正则表达式介绍 1.2 语法 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta http-equiv"X-UA-Compatible" content"IEedge"><meta name"viewpor…...

云硬盘和物理硬盘的区别
服务器的硬盘是服务器用来存储数据,一般有云硬盘和物理硬盘两种。云硬盘是云计算平台的虚拟技术的存储服务,将数据存储于云端通过分布式存储架构的形式。物理硬盘是将数据存储在服务器或者是PC端上,存储空间比较大,读写速度也很快…...

数据分析--观察数据处理异常值
引包: import pandas as pd import numpy as np 读取文件: dfpd.read_csv(./HR.csv) 文件见绑定资源(来自kaggle的HR.csv) 处理过程: 一、从df中拿出处理对象 二、找出缺失值的位置并删除 s1_sdf[satisfactio…...

vue3+elementPlus el-input的type=“number“时去除右边的上下箭头
改成 代码如下 <script lang"ts" setup> import {ref} from vue const inputBtn ref() </script> <template><el-input type"number" v-model"inputBtn" style"width: 80px;" class"no_number">…...
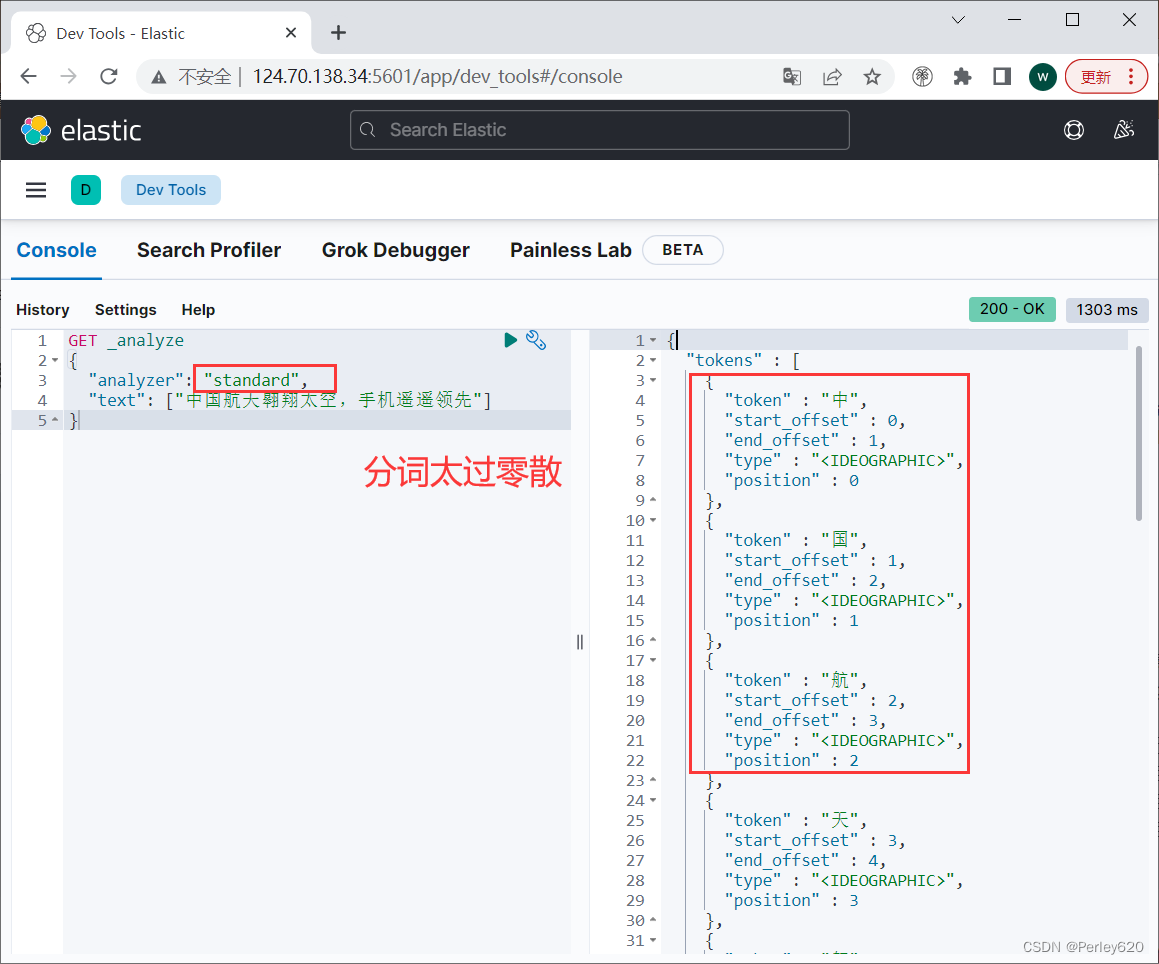
华为云云耀云服务器L实例评测|Elasticsearch的可视化Kibana工具安装 IK分词器的安装和使用
前言 最近华为云云耀云服务器L实例上新,也搞了一台来玩,期间遇到各种问题,在解决问题的过程中学到不少和运维相关的知识。 本篇博客介绍Elasticsearch的可视化Kibana工具安装,以及IK分词器的安装和使用。 其他相关的Elasticsea…...
)
加密货币交易技巧——人和(一)
交易原则 本篇主要讲述加密货币交易人需要注意的几个原则。 1.不能贪心,具体表现在做好仓位管理。第一,不要重仓进去,一定要轻仓。第二,开仓就想好本次要赚多少钱,不要太贪,到了预期点就止盈。第三&am…...

数学建模:最优化问题及其求解概述
数学建模:最优化问题及其求解概述 最优化问题定义分类离散优化问题连续优化问题 求解 此博客围绕运筹学以及最优化理论的相关知识,通俗易懂地介绍了最优化问题的定义、分类以及求解算法。 最优化问题 定义 数学优化(Mathematical Optimiza…...

企业办理CS资质,怎么选择办理等级?
信息系统建设和服务能力等级证书(Information system construction and service—Capability assessment system,简称:CS),由中国电子信息行业联合会组织开展的第三方评估活动,是根据《信息系统建设和服务能…...

华为云云耀云服务器L实例评测|Huawei Cloud EulerOS 自动化环境部署
[toc] Huawei Cloud EulerOS 自动化环境部署 云耀云服务器L实例【Huawei Cloud EulerOS 2.0 64bit】 Python Git Google Chrome Chromedriver Selenium More… 1. Python 镜像创建后自带。 2.Git 拉取项目。 sudo yum install git3. Google Chrome 使用root权限或sudo权…...
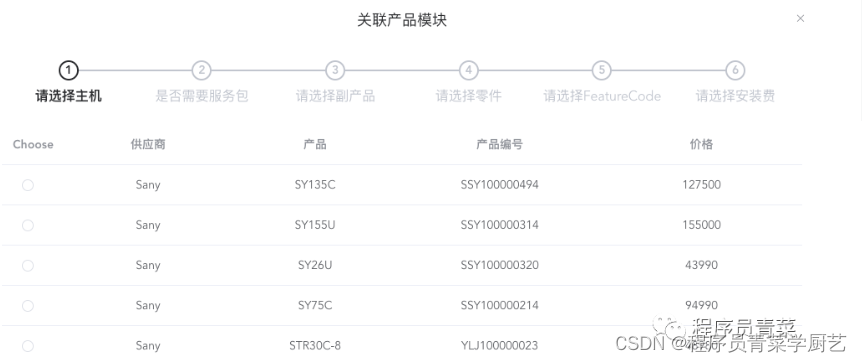
从一张表格开始做挖机报价系统
一、前言 历时4个月的挖机销售报价系统进入收尾阶段,由我直接负责与业务方对接,这中间各种折腾真是一言难尽,项目开发过程中还要维护POS系统以及牛奶配送系统,本项目我们采用的是迭代开发,今天讲一下具体的开发过程以…...
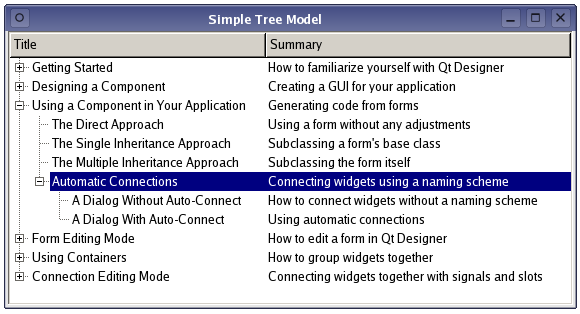
Qt扫盲-QTreeView 理论总结
QTreeView 理论使用总结 一、概述二、快捷键绑定三、提高性能四、简单实例1. 设计与概念2. TreeItem类定义3. TreeItem类的实现4. TreeModel类定义5. TreeModel类实现6. 在模型中设置数据 一、概述 QTreeView实现了 model 中item的树形表示。这个类用于提供标准的层次列表&…...

BF算法详解(JAVA语言实现)
目录 BF算法的介绍 图解 JAVA语言实现 BF算法的时间复杂度 BF算法的介绍 BF算法,即暴力(Brute Force)算法,是普通的模式匹配算法,BF算法的思想就是将目标串S的第一个字符与模式串T的第一个字符进行匹配,若相等,则继…...

零基础转行网络工程师,过来人给的一些建议
最近收到好多同学的一些提问,零基础没经验,能不能转行到网络工程师?薪资能有多少?发展前景怎么样? 应该有不少朋友都有这个疑问,那么,今天我尽量给大家做出一个详细的解答,希望能有…...

Vue中如何进行分布式搜索与全文搜索(如Elasticsearch)
在Vue中实现分布式搜索与全文搜索(使用Elasticsearch) 分布式搜索和全文搜索在现代应用程序中变得越来越重要,因为它们可以帮助用户快速查找和检索大量数据。Elasticsearch是一种强大的分布式搜索引擎,它可以用于实现高性能的全文…...
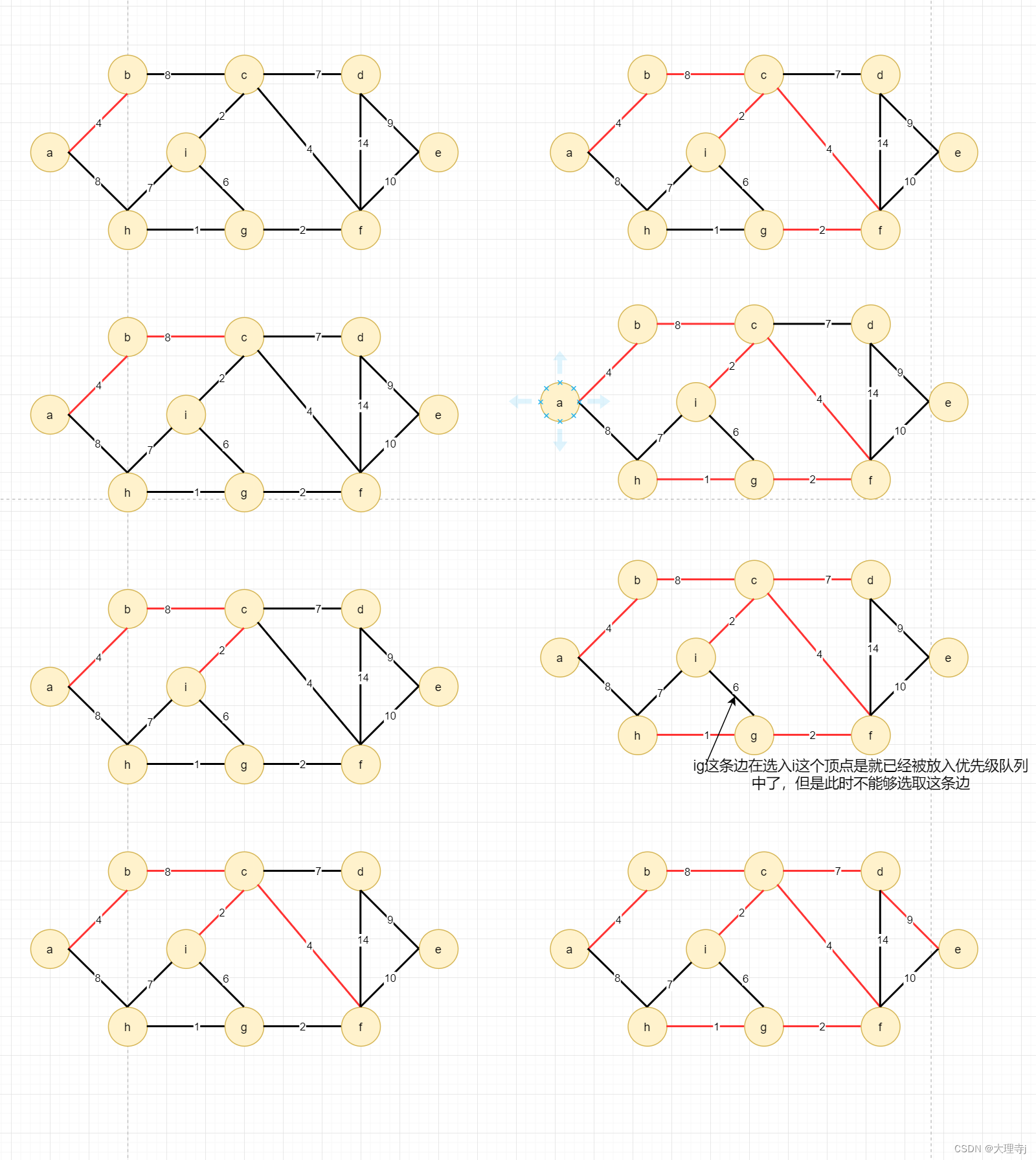
数据结构-图-最小生成树问题
最小生成树 并查集定义举例说明查找某个元素属于哪个集合代码实现路径压缩 Kruskal算法原理代码实现 Prim算法原理代码实现 并查集 定义 🚀在一些应用问题中,需要将n个不同的元素分成一些不相交的集合。开始时,每个元素自成一个单元素集合&…...
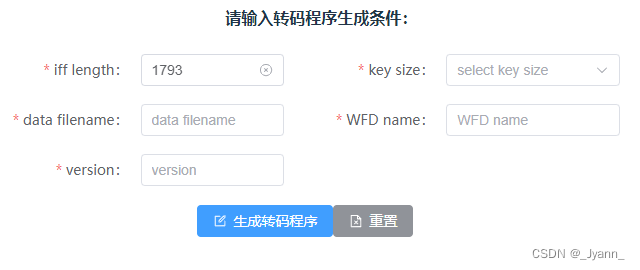
使用vite+npm封装组件库并发布到npm仓库
组件库背景:使用elementplusvue封装了一个通过表单组件。通过JSX对el-form下的el-input和el-button等表单进行统一封装,最后达到,通过数据即可一键生成页面表单的功能。 1.使用vite创建vue项目 npm create vitelatest elementplus-auto-form…...

85.最大矩形
单调栈,时间复杂度o(mn),空间复杂度o(mn) class Solution { public:int maximalRectangle(vector<vector<char>>& matrix) {int mmatrix.size();if(m0){return 0;}int nmatrix[0].size();//记录矩阵中每个元素左边连续1的数量vector<…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

DeepSeek源码深度解析 × 华为仓颉语言编程精粹——从MoE架构到全场景开发生态
前言 在人工智能技术飞速发展的今天,深度学习与大模型技术已成为推动行业变革的核心驱动力,而高效、灵活的开发工具与编程语言则为技术创新提供了重要支撑。本书以两大前沿技术领域为核心,系统性地呈现了两部深度技术著作的精华:…...

【安全篇】金刚不坏之身:整合 Spring Security + JWT 实现无状态认证与授权
摘要 本文是《Spring Boot 实战派》系列的第四篇。我们将直面所有 Web 应用都无法回避的核心问题:安全。文章将详细阐述认证(Authentication) 与授权(Authorization的核心概念,对比传统 Session-Cookie 与现代 JWT(JS…...


