【2357. 使数组中所有元素都等于零】
来源:力扣(LeetCode)
描述:
给你一个非负整数数组 nums 。在一步操作中,你必须:
- 选出一个正整数
x,x需要小于或等于nums中 最小 的 非零 元素。 nums中的每个正整数都减去x。
返回使 nums 中所有元素都等于 0 需要的 最少 操作数。
示例 1:
输入:nums = [1,5,0,3,5]
输出:3
解释:
第一步操作:选出 x = 1 ,之后 nums = [0,4,0,2,4] 。
第二步操作:选出 x = 2 ,之后 nums = [0,2,0,0,2] 。
第三步操作:选出 x = 2 ,之后 nums = [0,0,0,0,0] 。
示例 2:
输入:nums = [0]
输出:0
解释:nums 中的每个元素都已经是 0 ,所以不需要执行任何操作。
提示:
- 1 <= nums.length <= 100
- 0 <= nums[i] <= 100
方法一:排序 + 模拟
这道题要求计算将非负整数数组 nums 中的所有元素减少到 0 的最少操作数。用 m 表示数组 nums 中的最小非零元素,则可以选择不超过 m 的正整数 x,将数组中的每个非零元素减 x。为了使操作数最少,应选择 x = m,理由如下。
- 当选择 x = m 时,经过一次操作之后,数组中的所有元素 m 都变成 0,且其余的所有非零元素都减少 m。
- 当选择 x < m 时,经过一次操作之后,数组中的所有元素 m 在减少 x 之后仍大于 0,为了使数组中的最小非零元素变成 0,至少还需要一次操作,因此至少需要两次操作使数组中的所有元素 m 都变成 0,且其余的所有非零元素都减少 m。
由于当 x < m 时使元素 m 变成 0 的操作数大于当 x = m 时使元素 m 变成 0 的操作数,且两种方案中,使元素 m 变成 0 之后,剩余的最小非零元素相同(所有非零元素都减少 m),因此只有当 x = m 时才能使操作数最少。
根据上述分析,应使用贪心策略使操作数最少,贪心策略为每次选择数组中的最小非零元素作为 x,将数组中的每个非零元素减 x。
可以根据贪心策略模拟操作过程,计算最少操作数。
首先将数组 nums 按升序排序,然后从左到右遍历排序后的数组 nums。对于每个遍历到的非零元素,该元素是数组中的最小非零元素,将该元素记为 x,将数组中的每个非零元素都减 x,将操作数加 1。遍历结束之后,即可得到最少操作数。
代码:
class Solution {
public:void subtract(vector<int>& nums, int x, int startIndex) {int length = nums.size();for (int i = startIndex; i < length; i++) {nums[i] -= x;}}int minimumOperations(vector<int>& nums) {int ans = 0;sort(nums.begin(), nums.end());int length = nums.size();for (int i = 0; i < length; i++) {if (nums[i] > 0) {subtract(nums, nums[i], i);ans++;}}return ans;}
};
执行用时:0 ms, 在所有 C++ 提交中击败了100.00%的用户
内存消耗:7.9 MB, 在所有 C++ 提交中击败了100.00%的用户
复杂度分析
时间复杂度:O(n2),其中 n 是数组 nums 的长度。排序需要 O(nlogn) 的时间,排序之后需要遍历数组一次,对于每个非零元素,将数组中的所有非零元素减去最小非零元素需要 O(n) 的时间,因此时间复杂度是 O(n2)。
空间复杂度:O(logn),其中 n 是数组 nums 的长度。排序需要 O(logn) 的递归调用栈空间。
方法二:哈希集合
由于每次操作都将数组中的所有非零元素减少一个相同的值,因此数组中的相等元素减少到 0 的操作数相等,数组中的不相等元素减少到 0 的操作数不相等。
又由于使用贪心策略操作时,每次操作都会将数组中的最小非零元素减少到 0,因此最少操作数等于数组中的不同非零元素的个数。
使用哈希集合存储数组中的所有非零元素,则哈希集合的大小等于数组中的不同非零元素的个数,即为最少操作数。
需要注意的是,由于目标是将数组中的所有元素减少 0,如果数组中的一个元素已经是 0 则不需要对该元素执行操作,因此只需要考虑数组中的不同非零元素的个数。
代码:
class Solution {
public:int minimumOperations(vector<int>& nums) {unordered_set<int> hashSet;for (int num : nums) {if (num > 0) {hashSet.emplace(num);}}return hashSet.size();}
};
执行用时:0 ms, 在所有 C++ 提交中击败了100.00%的用户
内存消耗:8.2 MB, 在所有 C++ 提交中击败了28.86%的用户
复杂度分析
时间复杂度:O(n),其中 n 是数组 nums 的长度。需要遍历数组一次,每个非零元素加入哈希集合的时间是 O(1)。
空间复杂度:O(n),其中 n 是数组 nums 的长度。哈希集合需要 O(n) 的空间。
author:LeetCode-Solution
相关文章:

【2357. 使数组中所有元素都等于零】
来源:力扣(LeetCode) 描述: 给你一个非负整数数组 nums 。在一步操作中,你必须: 选出一个正整数 x ,x 需要小于或等于 nums 中 最小 的 非零 元素。nums 中的每个正整数都减去 x。 返回使 n…...

什么品牌的游戏蓝牙耳机比较好?玩游戏延迟低的蓝牙耳机推荐
游戏耳机的出现其实最主要的作用就是让玩家能够更专注的沉浸在游戏世界内,在声音层面去享受游戏的沉浸感,游戏最重要的就是操作灵敏,需要快速通过声音来判断敌人走向,所以小编特意整理了一期玩游戏延迟低的蓝牙耳机。 一、南卡小…...

day 33 状态压缩dp
二维状态压缩dp对于解决哈密顿回路问题的状态压缩dp只能计算固定起点到其他点的总方案数或最小路径等回路计数小蓝现在在第一栋教学楼,他想要访问每栋教学楼正好一次,最终回到第一栋教学楼(即走一条哈密尔顿回路)可看做࿱…...
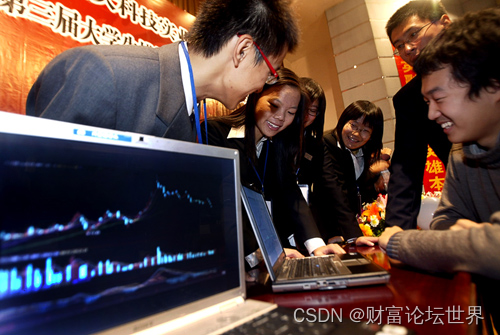
扬帆优配|超3600股飘绿,人民币贬值近300点!外资净卖近38亿
今天早盘,A股整体震动调整,白马蓝筹股体现较弱,上证50、沪深300指数均跌超1%。 盘面上,国防军工、造纸、数字钱银、IT设备等板块逆势活跃,酿酒、酒店餐饮、钙钛矿电池、有色等板块跌幅居前。两市半日成交4577亿&#x…...
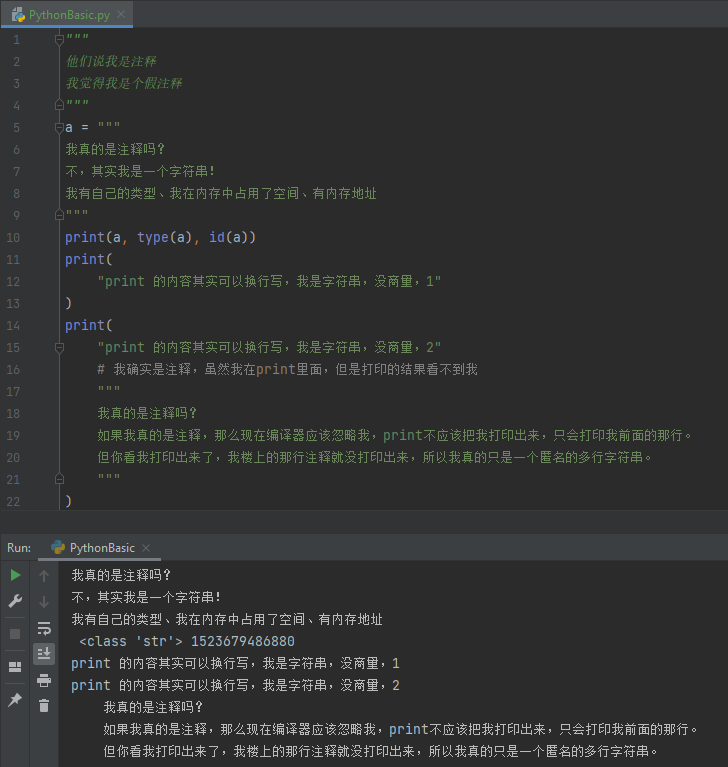
【编程基础之Python】6、Python基础知识
【编程基础之Python】6、Python基础知识Python基础知识Python的基本要素模块语句表达式注释Python的代码格式Python基础知识 Python 是一种高级的、动态的、解释型的编程语言,具有简单易学、开发效率高、可读性强等特点,广泛应用于数据科学、Web 开发、…...
selenium基本操作
爬虫与反爬虫之间的斗争爬虫:对某个网站数据或图片感兴趣,开始抓取网站信息;网站:请求次数频繁,并且访问ip固定,user_agent也是python,开始限制访问;爬虫:通过设置user_a…...
)
思科设备命令讲解(超基础二)
♥️作者:小刘在C站 ♥️个人主页:小刘主页 ♥️每天分享云计算网络运维课堂笔记,努力不一定有收获,但一定会有收获加油!一起努力,共赴美好人生! ♥️夕阳下,是最美的绽放࿰…...
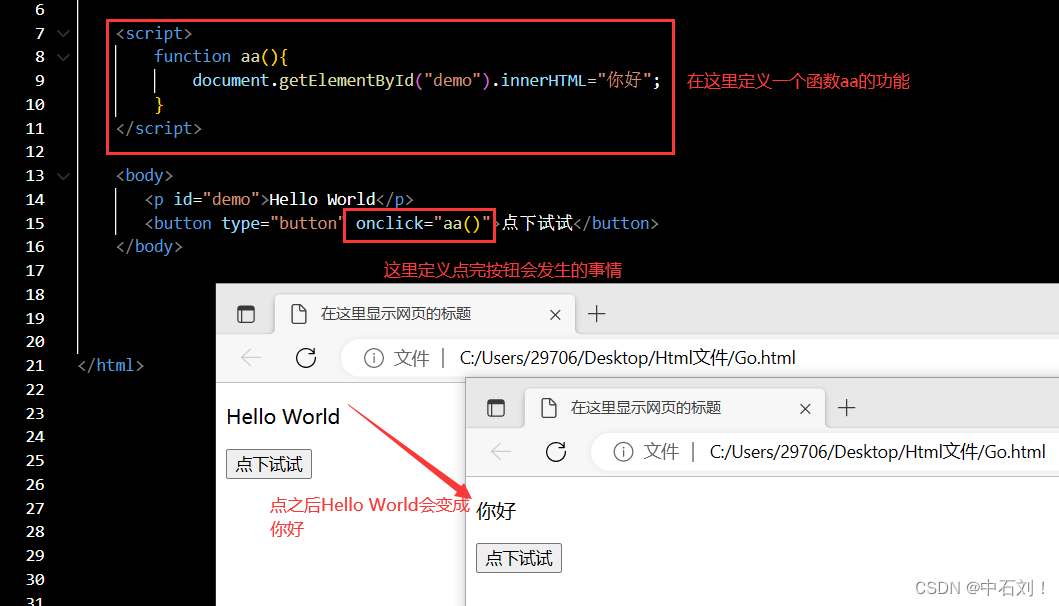
HTML基础(3)
HTML基础单选框、复选框、下拉框文本框< script >标签属性< script >基本使用单选框、复选框、下拉框 文本框 < script >标签属性 type属性定义script元素包含或src引用的脚本语言。属性值是MIME类型,包括text/javascript,text/ecmascript, appl…...
鸿蒙3.0 APP混合开发闪退问题笔记
APP采用cordova混合开发, 鸿蒙2.0以及安卓操作系统正常使用,但是在鸿蒙3.0中出现APP闪退,对APP进行真机调试发现,鸿蒙3.0系统对crosswork插件存在兼容问题,这些问题会导致APP页面加载失败,进而导致App闪退测…...
批量操作文件功能-课后程序(JAVA基础案例教程-黑马程序员编著-第七章-课后作业)
【实验7-1】 批量操作文件功能 任务介绍 1.任务描述 在日常工作中,经常会遇到批量操作系统文件的事情,通常情况下,只能手动重复的完成批量文件的操作,这样很是费时费力。本案例要求编写一个文件管理器,…...
Hadoop3.3.1完全分布式部署
Hadoop目录Hadoop3.3.1完全分布式部署(一)1、HDFS一、安装1、基础安装1.1、配置JDK-181.2、下载并解压hadoop安装包本地运行模式测试 eg:2、完全分布式运行模式1、概要:2、编写集群分发脚本,把1~4步安装的同步到其他服务器:2.1、创建脚本vim …...

SpringMVC中的注解
SpringMVC中的注解 文章目录SpringMVC中的注解RequestMapping注解RequestMapping中的value属性RequestMapping中的method属性派生类PathVariable注解RequestParam注解RequestMapping注解 RequestMapping中的value属性 RequestMapping:既可以标识在方法上也可以标识…...
python+Vue学生作业系统 django课程在线学习网站系统
系统分为学生,教师,管理员三个角色: 学生功能: 1.学生注册登录系统 2.学生查看个人信息,修改个人信息 3.学生查看主页综合评价,查看今日值班信息 4.学生在线申请请假信息,查看请假的审核结果和请…...
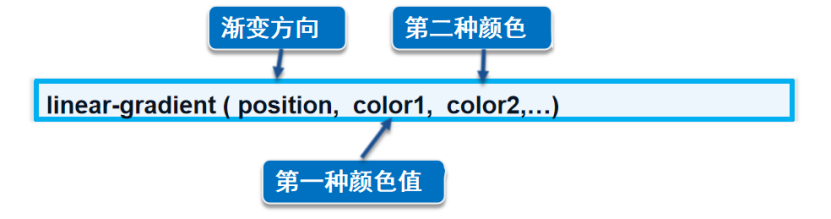
CSS 美化网页元素【快速掌握知识点】
目录 一、为什么使用CSS 二、字体样式 三、文本样式 color属性 四、排版文本段落 五、文本修饰和垂直对齐 1、文本装饰 2、垂直对齐方式 六、文本阴影 七、超链接伪类 1、语法 2、示例 3、访问时,蓝色;访问后,紫色; …...
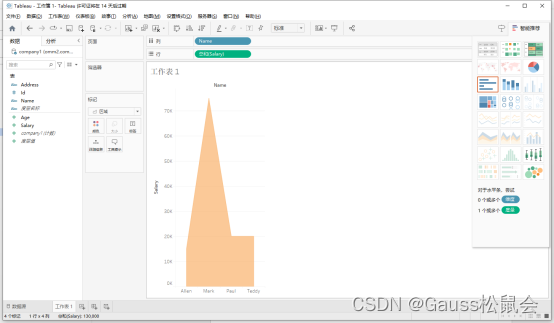
Tableau连接openGauss实践
目录 一、摘要 二、什么是Tableau? 三、安装Tableau 四、安装ODBC驱动 1、openGauss数据库 2、连接前置条件 3、Tableau连接openGauss方式一 4、Tableau连接openGauss方式二 一、摘要 Tableau可以连接到多种数据库,包括关系型数据库࿰…...

RabbitMQ 实现延迟队列
业务场景:1.生成订单30分钟未支付,则自动取消,我们该怎么实现呢?2.生成订单60秒后,给用户发短信1 安装rabbitMqwindows安装ubuntu中安装2 添加maven依赖<!-- https://mvnrepository.com/artifact/org.springframework.boot/spr…...
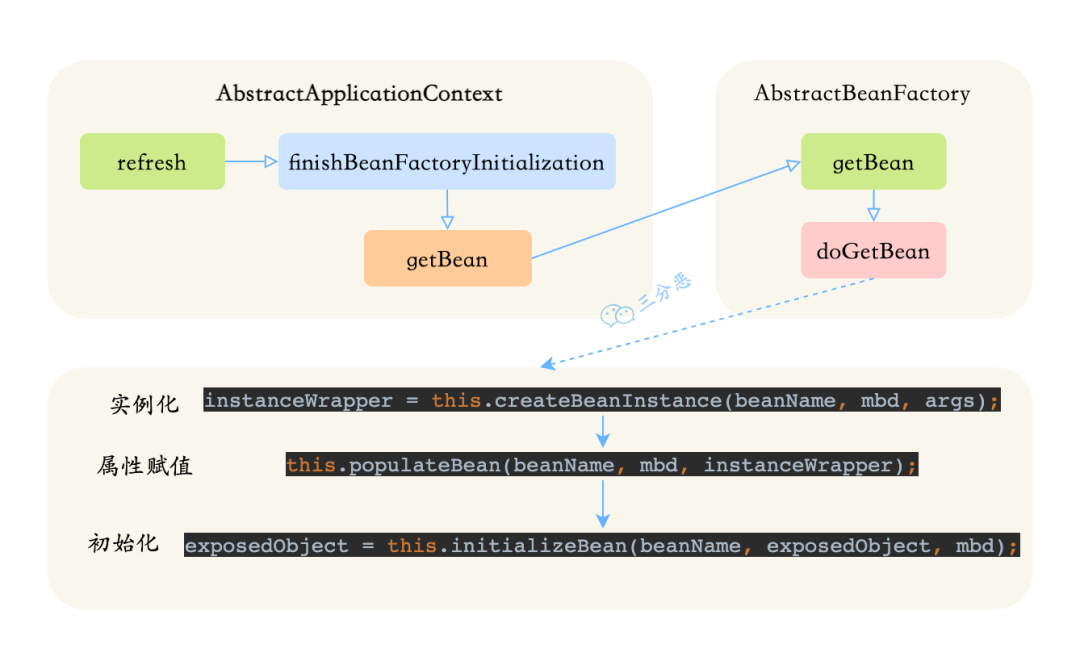
Spring Bean 生命周期,好像人的一生
简单说说IoC和Bean IoC,控制反转,想必大家都知道,所谓的控制反转,就是把new对象的权利交给容器,所有的对象都被容器控制,这就叫所谓的控制反转。 控制反转 Bean,也不是什么新鲜玩意儿…...

C++算法基础课 05 —— 数据结构1_单链表/双链表/栈/单调栈/队列/单调队列/KMP
文章目录 1. 单链表(用数组模拟链表)1.1 模板1.1.1 插入操作1.1.2 删除操作1.2 习题1 —— 826.单链表2. 双链表2.1 模板2.1.1 插入操作2.1.2 删除操作2.2 习题1 —— 827.双链表3. 栈(用数组模拟栈)3.1 模板3.2 习题1 —— 828.模拟栈4. 单调栈4.1 模板4.2 习题1 —— 830.单调…...

小型水库大坝安全监测的主要对象
一、监测背景 大坝监测的目的分成两个大的方面,一方面是为了验证设计、指导施工、为科研提供必要的资料;另一方面,也可以说是更重要的方面,就是为了长期监视大坝的安全运行。因此,一个成功的监测设计者不仅要能充分领会…...
版本介绍)
常见软件开源(alpha,beta等)版本介绍
一、开发期Alpha:是内部测试版,一般不向外部发布,会有很多Bug.一般只有测试人员使用。Beta:也是测试版,这个阶段的版本会一直加入新的功能。在Alpha版之后推出。-RC(ReleaseCandidate):最终测试版本;可能成为最终产品的…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

【入坑系列】TiDB 强制索引在不同库下不生效问题
文章目录 背景SQL 优化情况线上SQL运行情况分析怀疑1:执行计划绑定问题?尝试:SHOW WARNINGS 查看警告探索 TiDB 的 USE_INDEX 写法Hint 不生效问题排查解决参考背景 项目中使用 TiDB 数据库,并对 SQL 进行优化了,添加了强制索引。 UAT 环境已经生效,但 PROD 环境强制索…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...

OD 算法题 B卷【正整数到Excel编号之间的转换】
文章目录 正整数到Excel编号之间的转换 正整数到Excel编号之间的转换 excel的列编号是这样的:a b c … z aa ab ac… az ba bb bc…yz za zb zc …zz aaa aab aac…; 分别代表以下的编号1 2 3 … 26 27 28 29… 52 53 54 55… 676 677 678 679 … 702 703 704 705;…...

android RelativeLayout布局
<?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...

libfmt: 现代C++的格式化工具库介绍与酷炫功能
libfmt: 现代C的格式化工具库介绍与酷炫功能 libfmt 是一个开源的C格式化库,提供了高效、安全的文本格式化功能,是C20中引入的std::format的基础实现。它比传统的printf和iostream更安全、更灵活、性能更好。 基本介绍 主要特点 类型安全:…...

ubuntu系统文件误删(/lib/x86_64-linux-gnu/libc.so.6)修复方案 [成功解决]
报错信息:libc.so.6: cannot open shared object file: No such file or directory: #ls, ln, sudo...命令都不能用 error while loading shared libraries: libc.so.6: cannot open shared object file: No such file or directory重启后报错信息&…...
