【gcc】RtpTransportControllerSend学习笔记 3：gcc
- 本文是大神 https://www.cnblogs.com/ishen 的文章的学习笔记。
- 大神的webrtc源码分析(8)-拥塞控制(上)-码率预估 详尽而具体，堪称神作。
- 本文使用的代码是m79 ，与大神有不同。
- 2.4 Probe只会在一些特殊的时候才会进行探测(链路刚开始时, 码率不正常暴跌时)
- 2.5 ： 对发送的吞吐量进行估算
2.5 吞吐量-AcknowledgedBitrateEstimator
- D:\zhb-dev\gerrit\livecloud\src\third_party\webrtc\modules\congestion_controller\goog_cc\acknowledged_bitrate_estimator.h
class AcknowledgedBitrateEstimator {public:AcknowledgedBitrateEstimator(const WebRt相关文章：
【gcc】RtpTransportControllerSend学习笔记 3：gcc
本文是大神 https://www.cnblogs.com/ishen 的文章的学习笔记。大神的webrtc源码分析(8)-拥塞控制(上)-码率预估 详尽而具体，堪称神作。本文使用的代码是m79 ，与大神有不同。2.4 Probe只会在一些特殊的时候才会进行探测(链路刚开始时, 码率不正常暴跌时)2.5 ： 对发送的吞吐量…...
CSP-J第二轮试题-2019年-3题
文章目录 参考：总结 [CSP-J2019] 纪念品题目描述输入格式输出格式样例 #1样例输入 #1样例输出 #1 样例 #2样例输入 #2样例输出 #2 提示答案 现场真题注意事项 参考： P5662 CSP-J2019纪念品 总结 本系列为CSP-J/S算法竞赛真题讲解，会按照年…...
数据库：Hive转Presto（三）
继续上节代码。 import re import os import tkinter.filedialog from tkinter import *class Hive2Presto:def __int__(self):self.t_funcs [substr, nvl, substring, unix_timestamp] \[to_date, concat, sum, avg, abs, year, month, ceiling, floor]self.time_funcs [d…...
【AI视野·今日Robot 机器人论文速览 第四十八期】Thu, 5 Oct 2023
AI视野今日CS.Robotics 机器人学论文速览 Thu, 5 Oct 2023 Totally 32 papers 👉上期速览✈更多精彩请移步主页 Daily Robotics Papers LanguageMPC: Large Language Models as Decision Makers for Autonomous Driving Authors Hao Sha, Yao Mu, Yuxuan Jiang, Li…...
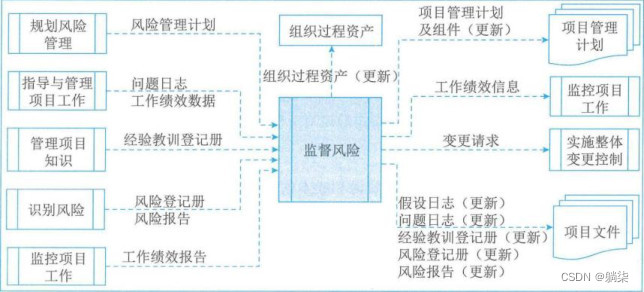
学信息系统项目管理师第4版系列20_风险管理
1. 针对不确定性的应对方法 1.1. 【高23上选58】 1.2. 收集信息 1.2.1. 可以对信息收集和分析工作进行规划，以便发现更多信息（如进行研究、争取专家参与或进行市场分析）来减少不确定性 1.3. 为多种结果做好准备 1.3.1. 制定可用的解决方…...
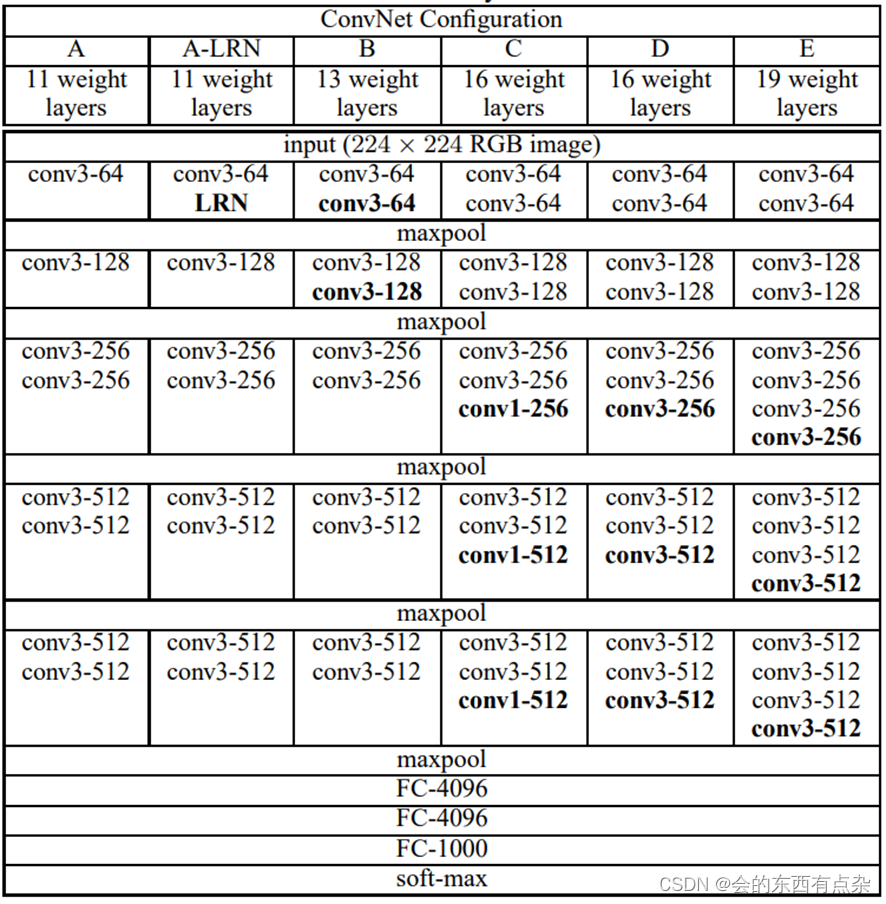
卷积神经网络的发展历史-VGG
VGG的产生 2014 年，Simonyan和Zisserman提出了VGG系列模型（包括VGG-11/VGG-13/VGG-16/VGG-19），并在当年的ImageNet Challenge上作为分类任务第二名、定位（Localization）任务第一名的基础网络出现。 VGG的…...
qt解决信号和槽连接时传递额外参数的问题
解决信号和槽连接时传递额外参数的问题 QSignalMapper 是 Qt 框架中的一个类，用于解决信号和槽连接时传递额外参数的问题。当一个信号被触发时，QSignalMapper 可以将该信号与一个特定的参数关联起来，并将信号与对应的槽函数进行连接。 下面…...
『力扣每日一题14』：消失的数字
昨天忙过头，等想起来已经 12 点多了，于是乎断更了。在这里先跟广大读者说声抱歉，并且稍后我会再更一篇。 一、题目 数组nums包含从0到n的所有整数，但其中缺了一个。请编写代码找出那个缺失的整数。你有办法在O(n)时间内完成吗&…...
【b站韩顺平 快速学Java课】Java的JDK8（包括公共JRE8）安装教程 总结
最近开始学Java，如果是程序员的话要使用Java——需要安装JDK。 不同操作系统（Win/Linux/Mac）——需要安装不同的JDK。 1.JDK安装官网链接： Java Downloads | Oracle 我的电脑是win x64,以下笔记总结就暂且以本人电脑操作系统版本…...
Spark 弹性分布式数据集 RDD
1.RDD简介 `RDD` 全称为 Resilient Distributed Datasets，是 Spark 最基本的数据抽象，它是只读的、分区记录的集合，支持并行操作，可以由外部数据集或其他 RDD 转换而来，它具有以下特性： 一个 RDD 由一个或者多个分区（Partitions）组成。对于 RDD 来说，每个分区会被一个…...
电脑被删除的文件怎么恢复？2023年数据恢复方法分享
大多数人在使用电脑时都可能会遇到误删文件的情况。一不小心，重要的文件或数据就消失了，情急之下，大多会感到慌乱和无助。但其实，文件误删除并非不可挽回的灾难。本文将为大家介绍几种有效的文件恢复方法，以帮助大家在…...
李宏毅 2022机器学习 HW3 boss baseline 上分记录
作业数据是所有数据都有标签的版本。 李宏毅 2022机器学习 HW3 boss baseline 上分记录 1. 训练数据增强2. cross validation&ensemble3. test dataset augmentation4. resnet 1. 训练数据增强 结论：训练数据增强、更长时间的训练、dropout都证明很有效果&…...
SpringBatch适配不同数据库的两种方法
一、配置JobRepository Configuration EnableBatchProcessing public class TaskArrangeConfig extends DefaultBatchConfigurer {Autowiredprivate DataSource dataSource;Autowiredprivate JobLauncher jobLauncher;Autowiredprivate JobExplorer jobExplorer;Autowiredpriv…...
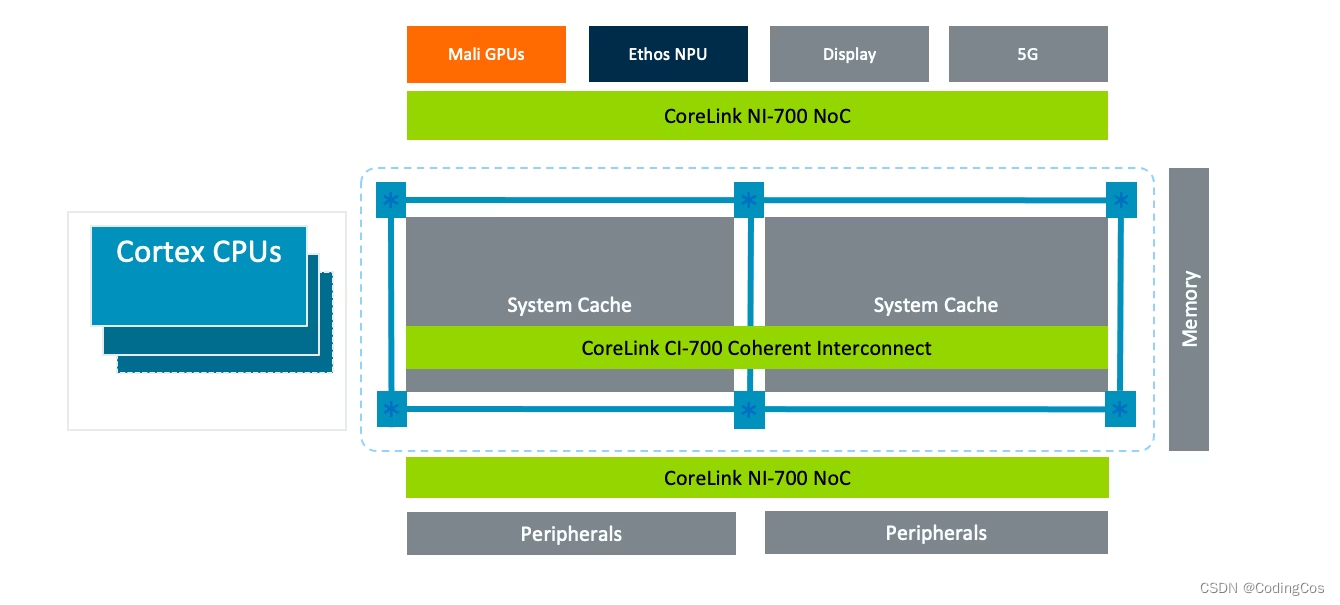
【ARM CoreLink 系列 5 -- CI-700 控制器介绍 】
文章目录 1.1 什么是 CI-700？1.1.1 关于 CI-7001.1.2 CI-700 特点1.2 全局配置参数1.2.1 寻址能力1.3 组件和配置1.3.1 CI-700 互联的结构1.3.2 Crosspoint(XP)1.3.3 外部接口1.4 组件(Components)1.1 什么是 CI-700？ CI-700是一种AMBA 5 CHI互连，具有可定制的网状拓扑结构…...
找不到msvcp140_1.dll怎么办，快速解决msvcp140_1.dll问题的方法分享
在日常使用计算机的过程中，经常会遇到一些程序无法正常运行的问题，其中最常见的就是“msvcp140_1.dll丢失”。这是一个典型的DLL文件丢失问题，但背后的原因却往往并不简单。通过深入研究这个问题，我对其有了更深入的理解。 首先&a…...
华为云云耀云服务器L实例评测｜部署私有网盘 Nextcloud
华为云云耀云服务器L实例评测｜部署私有网盘 Nextcloud 一、云耀云服务器L实例介绍1.1 云服务器介绍1.2 产品规格1.3 应用场景 二、云耀云服务器L实例配置2.1 重置密码2.2 服务器连接2.3 安全组配置 三、部署 Nextcloud3.1 Nextcloud 介绍3.2 Docker 环境搭建3.3 Nex…...
vue3中使用插件vite-plugin-svg-icons
在vue3 vite 项目中使用svg图标 插件：vite-plugin-svg-icons 预加载 在项目运行时就生成所有图标,只需操作一次 dom高性能 内置缓存,仅当文件被修改时才会重新生成 安装 yarn add vite-plugin-svg-icons -D # or npm i vite-plugin-svg-icons -D # or pnpm inst…...
面试题20231008
前端 2023年前端面试题汇总-CSDN博客 后端 1.Java基础 容器、线程等等 a.JDK 和 JRE 有什么区别？ JDK：Java Development Kit 的简称，Java 开发工具包，提供了 Java 的开发环境和运行环境。 JRE：Java Runtime Envir…...
2023全新小红书图集和视频解析去水印网站源码
2023全新小红书图集和视频解析去水印网站源码 小红书视频图集解析网站源码，在红书看到好看的图片以及好看的头像，但是直接下载又有水印就非常难受，这个可以一键解析去除水印，支持统计解析次数，本地接口。 源码下载&a…...
2023去水印小程序源码修复版-前端后端内置接口+第三方接口
去水印小程序源码，前端后端，内置接口第三方接口，修复数据库账号密码错误问题，内置接口支持替换第三方接口，看了一下文件挺全的，可以添加流量主代码，搭建需要准备一台服务器，备案域名…...
树莓派智能画布：从Raspbian部署到NeoPixel灯光系统集成
1. 项目概述：打造一个会发光的智能画布如果你和我一样，对嵌入式硬件和创意编程的结合着迷，那么将一块普通的画布变成一个由代码控制的动态灯光装置，绝对是一件充满乐趣和成就感的事情。这个项目，我称之为“CompuCanvas…...
ClawForgeAI：基于工作流编排的AIGC创意自动化平台解析
1. 项目概述：从“ClawForgeAI/clawforge”看AI驱动的创意工具新范式最近在GitHub上看到一个挺有意思的项目，叫“ClawForgeAI/clawforge”。光看这个名字，你可能会有点摸不着头脑——“ClawForge”听起来像是个游戏模组工具或者某种机械设计软…...
AI智能体技能库开发实战：从工具调用到系统集成
1. 项目概述：一个智能体技能库的诞生如果你正在研究或开发AI智能体，尤其是基于大型语言模型（LLM）的自主智能体，那么你一定遇到过这样的困境：智能体的核心能力，除了模型本身的理解和生成…...
STM32H7网络通信避坑指南：CubeMX配置LWIP 2.1.2时，这几个DCache和ETH的选项千万别选错
STM32H7网络通信避坑指南：CubeMX配置LWIP 2.1.2的关键陷阱解析 在STM32H7系列开发中，以太网通信的稳定性往往成为项目成败的分水岭。许多开发者在使用CubeMX配置LWIP 2.1.2协议栈时，明明按照官方文档一步步操作，却在实战中遭遇数据…...
AI应用开发利器：NeuroAPI网关统一管理多模型调用与部署实战
1. 项目概述：一个面向AI应用开发的API网关最近在折腾AI应用开发的朋友，估计都绕不开一个头疼的问题：模型管理。今天想试试Claude，明天项目需要接入GPT-4，后天可能又要调用一个开源的Llama模型。每个模型都有自己的API地…...
硬件预取技术：Alecto框架优化与性能提升
1. 硬件预取技术基础与挑战在现代处理器架构中，内存墙（Memory Wall）问题一直是制约性能提升的关键瓶颈。随着CPU与DRAM之间的速度差距不断拉大，硬件预取技术已成为缓解这一问题的核心手段。传统预取器通过分析程序的内存访问模式&…...
深入聊聊Zynq RFSoC里那些容易搞混的时钟：从外部输入到片内PLL再到AXI-Stream接口时钟
深入解析Zynq RFSoC时钟架构：从外部输入到AXI-Stream接口的完整路径 在Zynq UltraScale RFSoC的设计中，时钟系统堪称整个架构的"心脏"。尤其当涉及多通道同步、跨时钟域数据传输等高阶应用时，时钟配置的细微差别往往会导致性能差异…...
t-io HTTP服务器实现：如何替代Tomcat和Jetty的完整指南
t-io HTTP服务器实现：如何替代Tomcat和Jetty的完整指南 【免费下载链接】t-io T-io is a network programming framework developed based on Java AIO. From the collected cases, t-io is widely used for IoT, IM, and customer service, making it a top-notch …...
ClawPowers-Skills：开发者实战技能库与个人工具箱构建指南
1. 项目概述与核心价值最近在GitHub上看到一个挺有意思的项目，叫“ClawPowers-Skills”，作者是up2itnow0822。乍一看这个标题，你可能会有点摸不着头脑——“ClawPowers”是什么？“Skills”又具体指什么？这其实是一个典…...