机器学习笔记之近似推断(一)从深度学习角度认识推断
机器学习笔记之近似推断——从深度学习角度认识推断
- 引言
- 推断——基本介绍
- 精确推断难的原因
- 虽然能够表示,但计算代价太大
- 无法直接表示
引言
本节是一篇关于推断总结的博客,侧重点在于深度学习模型中的推断任务。
推断——基本介绍
推断(Inference\text{Inference}Inference)——我们并不陌生,在介绍的每一个概率模型,基本都涉及到推断问题。关于概率模型的三大核心问题分别是:表示(Representation\text{Representation}Representation),推断,学习(Learning\text{Learning}Learning)。我们从深度模型,主要是深度生成模型所涉及的推断任务出发,对推断进行描述。
首先,是什么样的原因,导致了推断这个任务的发生?换句话说,推断的动机是什么。
-
我们基于可观察的样本特征X\mathcal XX,构建概率图模型。如果包含隐变量Z\mathcal ZZ,而隐变量Z\mathcal ZZ绝大多数情况下没有物理意义,它只是我们建模过程中人工设置出来的随机变量。
Z\mathcal ZZ一上来就是未知的,但为了完善被构建的模型,我们有必要了解隐变量Z\mathcal ZZ的特征信息。从哪里去了解/通过什么渠道去了解Z\mathcal ZZ? 从 样本X\mathcal XX。
当样本X\mathcal XX进入到模型后,Z\mathcal ZZ会产生什么样的反映,而这个反映就是隐变量Z\mathcal ZZ的特征信息,即P(Z∣X)\mathcal P(\mathcal Z \mid \mathcal X)P(Z∣X)。而推断就是求解Z\mathcal ZZ特征信息P(Z∣X)\mathcal P(\mathcal Z \mid \mathcal X)P(Z∣X)的手段。因此:推断的第一个动机就是推断自身。我们需要通过样本X\mathcal XX的渠道,将Z\mathcal ZZ的特征信息描述出来。
-
关于推断的另一个动机来自于模型的学习任务。也就是说,在模型参数θ\thetaθ的学习过程中,可能存在 不可避免地使用推断。
一个经典例子就是受限玻尔兹曼机(Restricted Boltzmann Machine,RBM\text{Restricted Boltzmann Machine,RBM}Restricted Boltzmann Machine,RBM)。在受限玻尔兹曼机基于极大似然估计来求解对数似然梯度∇θ[logP(v(i);θ)]\nabla_{\theta} \left[\log \mathcal P(v^{(i)};\theta)\right]∇θ[logP(v(i);θ)]的过程中,可将对数似然梯度描述为如下形式:
需要注意的是,针对某个观测样本v(i)v^{(i)}v(i),我们并没有将所有参数的对数似然梯度都求出来,仅求解的是v(i)v^{(i)}v(i)中某一随机变量vj(i)v_j^{(i)}vj(i)与对应模型中隐变量h(i)h^{(i)}h(i)的某一随机变量hk(i)h_k^{(i)}hk(i)之间的模型参数Wvj(i)⇔hk(i)\mathcal W_{v_j^{(i)} \Leftrightarrow h_k^{(i)}}Wvj(i)⇔hk(i)的对数似然梯度。关于hj(i)h_j^{(i)}hj(i)是一个服从‘伯努利分布’的随机变量,完整推导过程见上述链接。
∇θ[logP(v(i);θ)]⇒∂∂Wvj(i)⇔hk(i)[logP(v(i);θ)]=P(hk(i)=1∣v(i))⋅vj(i)⏟第一项−∑v(i)P(v(i))⋅P(hk(i)=1∣v(i))⋅vj(i)⏟第二项\begin{aligned} \nabla_{\theta} \left[\log \mathcal P(v^{(i)};\theta)\right] & \Rightarrow \frac{\partial}{\partial \mathcal W_{v_j^{(i)} \Leftrightarrow h_k^{(i)}}} \left[\log \mathcal P(v^{(i)};\theta)\right] \\ & = \underbrace{\mathcal P(h_k^{(i)} = 1 \mid v^{(i)}) \cdot v_j^{(i)}}_{第一项} - \underbrace{\sum_{v^{(i)}} \mathcal P(v^{(i)}) \cdot \mathcal P(h_k^{(i)} = 1 \mid v^{(i)}) \cdot v_j^{(i)}}_{第二项} \end{aligned}∇θ[logP(v(i);θ)]⇒∂Wvj(i)⇔hk(i)∂[logP(v(i);θ)]=第一项P(hk(i)=1∣v(i))⋅vj(i)−第二项v(i)∑P(v(i))⋅P(hk(i)=1∣v(i))⋅vj(i)
关于上述的对数似然梯度结果,第一项中的P(hk(i)=1∣v(i))\mathcal P(h_k^{(i)} = 1 \mid v^{(i)})P(hk(i)=1∣v(i))就用到了后验概率的推断结果:
推导过程详见受限玻尔兹曼机——推断任务(后验概率),这里nnn表示v(i)v^{(i)}v(i)中随机变量结点的个数。
P(hk(i)=1∣v(i))=Sigmoid(∑j=1nWhk(i)⇔vj(i)⋅vj(i)+ck(i))\mathcal P(h_k^{(i)} = 1 \mid v^{(i)}) = \text{Sigmoid}\left(\sum_{j=1}^n \mathcal W_{h_k^{(i)}\Leftrightarrow v_j^{(i)}} \cdot v_j^{(i)} + c_k^{(i)}\right)P(hk(i)=1∣v(i))=Sigmoid(j=1∑nWhk(i)⇔vj(i)⋅vj(i)+ck(i))
这明显是一个精确推断(Precise Inference\text{Precise Inference}Precise Inference)。相反,同样使用推断的方式进行求解,使用对比散度这种近似推断的方式加快采样速度。
由于这里重点描述的是‘推断’与‘学习任务’之间的关联关系,这里就不展开求解了.另一个经典例子就是EM\text{EM}EM算法(Expectation Maximization,EM\text{Expectation Maximization,EM}Expectation Maximization,EM)。它的E\text{E}E步可表示为如下形式:
logP(X;θ)=∫ZQ(Z)⋅logP(X∣θ)dZ=∫ZQ(Z)logP(X,Z;θ)Q(Z)dZ⏟ELBO+{−∫ZQ(Z)logP(Z∣X)Q(Z)dZ}⏟KL Divergence\begin{aligned} \log \mathcal P(\mathcal X ; \theta) & = \int_{\mathcal Z} \mathcal Q(\mathcal Z) \cdot \log \mathcal P(\mathcal X \mid \theta) d\mathcal Z \\ & = \underbrace{\int_{\mathcal Z} \mathcal Q(\mathcal Z) \log \frac{\mathcal P(\mathcal X,\mathcal Z;\theta)}{\mathcal Q(\mathcal Z)}d\mathcal Z}_{\text{ELBO}} + \underbrace{\left\{- \int_{\mathcal Z} \mathcal Q(\mathcal Z) \log \frac{\mathcal P(\mathcal Z \mid \mathcal X)}{\mathcal Q(\mathcal Z)} d\mathcal Z\right\}}_{\text{KL Divergence}} \end{aligned}logP(X;θ)=∫ZQ(Z)⋅logP(X∣θ)dZ=ELBO∫ZQ(Z)logQ(Z)P(X,Z;θ)dZ+KL Divergence{−∫ZQ(Z)logQ(Z)P(Z∣X)dZ}
其中X\mathcal XX是基于样本的随机变量集合;Q(Z)\mathcal Q(\mathcal Z)Q(Z)是人为设定的、关于隐变量Z\mathcal ZZ的分布;如果关于Z\mathcal ZZ的后验分布P(Z∣X)\mathcal P(\mathcal Z \mid \mathcal X)P(Z∣X)可求解,即Q(Z)=P(Z∣X)\mathcal Q(\mathcal Z) = \mathcal P(\mathcal Z \mid \mathcal X)Q(Z)=P(Z∣X),那么此时KL Divergence=0\text{KL Divergence} = 0KL Divergence=0,自然可以使用参数迭代逼近 的方式对模型参数θ\thetaθ进行迭代求解:
其中的Q(Z)=P(Z∣X)\mathcal Q(\mathcal Z) = \mathcal P(\mathcal Z \mid \mathcal X)Q(Z)=P(Z∣X)明显是一种对P(Z∣X)\mathcal P(\mathcal Z \mid \mathcal X)P(Z∣X)的精确推断。
{logP(X;θ)=ELBO(KL Divergence=0)θ(t+1)=argmaxθ[∫ZP(Z∣X,θ(t))logP(X,Z;θ)dZ]\begin{cases} \log \mathcal P(\mathcal X;\theta) = \text{ELBO} \quad (\text{KL Divergence} = 0) \\ \theta^{(t+1)} = \mathop{\arg\max}\limits_{\theta} \left[\int_{\mathcal Z} \mathcal P(\mathcal Z \mid \mathcal X,\theta^{(t)}) \log \mathcal P(\mathcal X , \mathcal Z;\theta) d\mathcal Z\right] \end{cases}⎩⎨⎧logP(X;θ)=ELBO(KL Divergence=0)θ(t+1)=θargmax[∫ZP(Z∣X,θ(t))logP(X,Z;θ)dZ]
但实际情况下,关于隐变量Z\mathcal ZZ的后验分布P(Z∣X)\mathcal P(\mathcal Z \mid \mathcal X)P(Z∣X)可能无法精确求解,此时Q(Z)\mathcal Q(\mathcal Z)Q(Z)的作用就是逼近当前迭代步骤中的P(Z∣X)\mathcal P(\mathcal Z \mid \mathcal X)P(Z∣X),使得当前迭代步骤的ELBO\text{ELBO}ELBO达到最大;再将当前迭代步骤最优近似分布Q(Z)\mathcal Q(\mathcal Z)Q(Z)带回ELBO\text{ELBO}ELBO中,从而求出当前迭代步骤的最优参数。这就是广义EM\text{EM}EM算法:相对于EM算法过程,因P(Z∣X)\mathcal P(\mathcal Z \mid \mathcal X)P(Z∣X)自身无法精确求解的问题,广义EM算法使得分布Q(Z)≈P(Z∣X)\mathcal Q(\mathcal Z) \approx \mathcal P(\mathcal Z \mid \mathcal X)Q(Z)≈P(Z∣X)这明显是一种近似推断。下面描述给定ttt时刻模型参数θ(t)\theta^{(t)}θ(t)的条件下,求解t+1t+1t+1时刻E\text{E}E步的近似分布Q^(t+1)(Z)\hat {\mathcal Q}^{(t+1)}(\mathcal Z)Q^(t+1)(Z)与t+1t+1t+1时刻M\text{M}M步最优参数θ(t+1)\theta^{(t+1)}θ(t+1)的过程。
{Q^(t+1)(Z)=argmaxQ(Z)∫ZQ(Z)logP(X,Z;θ(t))Q(Z)dZ⏟ELBO⇔argminQ(Z)−∫ZQ(Z)logP(Z∣X)Q(Z)dZ⏟KL Divergenceθ(t+1)=argmaxθ∫ZQ^(t+1)(Z)logP(X,Z;θ)Q^(t+1)(Z)dZ⏟ELBO\begin{cases} \hat {\mathcal Q}^{(t+1)}(\mathcal Z) = \mathop{\arg\max}\limits_{\mathcal Q(\mathcal Z)} \underbrace{\int_{\mathcal Z} \mathcal Q(\mathcal Z) \log \frac{\mathcal P(\mathcal X,\mathcal Z;\theta^{(t)})}{\mathcal Q(\mathcal Z)} d\mathcal Z}_{\text{ELBO}} \Leftrightarrow \mathop{\arg\min}\limits_{\mathcal Q(\mathcal Z)} \underbrace{- \int_{\mathcal Z} \mathcal Q(\mathcal Z) \log \frac{\mathcal P(\mathcal Z \mid \mathcal X)}{\mathcal Q(\mathcal Z)} d\mathcal Z}_{\text{KL Divergence}}\\ \theta^{(t+1)} = \mathop{\arg\max}\limits_{\theta} \underbrace{\int_{\mathcal Z} \hat {\mathcal Q}^{(t+1)}(\mathcal Z) \log \frac{\mathcal P(\mathcal X,\mathcal Z ;\theta)}{\hat {\mathcal Q}^{(t+1)}(\mathcal Z)}d\mathcal Z}_{\text{ELBO}} \end{cases}⎩⎨⎧Q^(t+1)(Z)=Q(Z)argmaxELBO∫ZQ(Z)logQ(Z)P(X,Z;θ(t))dZ⇔Q(Z)argminKL Divergence−∫ZQ(Z)logQ(Z)P(Z∣X)dZθ(t+1)=θargmaxELBO∫ZQ^(t+1)(Z)logQ^(t+1)(Z)P(X,Z;θ)dZ
这两个模型参数学习的例子(一个是学习参数梯度,一个是迭代学习参数),它们都不可避免地对隐变量的后验分布进行推断。
精确推断难的原因
虽然能够表示,但计算代价太大
为什么要近似推断?最核心的原因是:精确推断非常困难。也就是说,精确推断的代价太大了。
- 依然以上述受限玻尔兹曼机对数似然梯度求解过程中的第二项为例:
∑v(i)P(v(i))⋅P(hk(i)=1∣v(i))⋅vj(i)\sum_{v^{(i)}} \mathcal P(v^{(i)}) \cdot \mathcal P(h_k^{(i)} = 1 \mid v^{(i)}) \cdot v_j^{(i)}v(i)∑P(v(i))⋅P(hk(i)=1∣v(i))⋅vj(i)
其中,∑v(i)\sum_{v^{(i)}}∑v(i)表示样本数量的连加项,有NNN项;如果观测变量V\mathcal VV中包含nnn个随机变量,即:v(i)=(v1(i),v2(i),⋯,vn(i))n×1Tv^{(i)} = (v_1^{(i)},v_2^{(i)},\cdots,v_n^{(i)})_{n \times 1}^Tv(i)=(v1(i),v2(i),⋯,vn(i))n×1T,并且各观测变量之间相互独立且均服从伯努利分布。那么P(v(i))\mathcal P(v^{(i)})P(v(i))可表示为如下形式:
P(v(i))=∏m=1nP(vm(i))\mathcal P(v^{(i)}) = \prod_{m=1}^n \mathcal P(v_m^{(i)})P(v(i))=m=1∏nP(vm(i))
仅仅P(v(i))\mathcal P(v^{(i)})P(v(i))一项的复杂度就是O(2n)\mathcal O(2^n)O(2n);暂时不考虑P(hk(i)=1∣v(i))\mathcal P(h_k^{(i)} = 1 \mid v^{(i)})P(hk(i)=1∣v(i))中Sigmoid\text{Sigmoid}Sigmoid函数内线性计算的复杂度,上式中的复杂度 至少是O(N⋅2n)\mathcal O(N\cdot 2^n)O(N⋅2n)。能算吗?能算,但样本足够多的情况下,代价可看作是无穷大。
这还仅仅是将随机变量设置成最简单的伯努利分布,如果复杂度出现‘指数级别’,就可看做是‘无法求解的’(Intractable\text{Intractable}Intractable).
上述的例子可以根据受限玻尔兹曼机自身关于随机变量的约束能够将复杂的概率分布进行分解,只是分解出的结果计算量太大;
无法直接表示
然而存在一些模型,模型内部随机变量关联关系复杂的同时,还十分没有章法。最终导致联合概率分布连分解都做不到。
-
例如玻尔兹曼机(Boltzmann Machine,BM\text{Boltzmann Machine,BM}Boltzmann Machine,BM),它本质上就是一个由观测变量、隐变量构成的马尔可夫随机场:
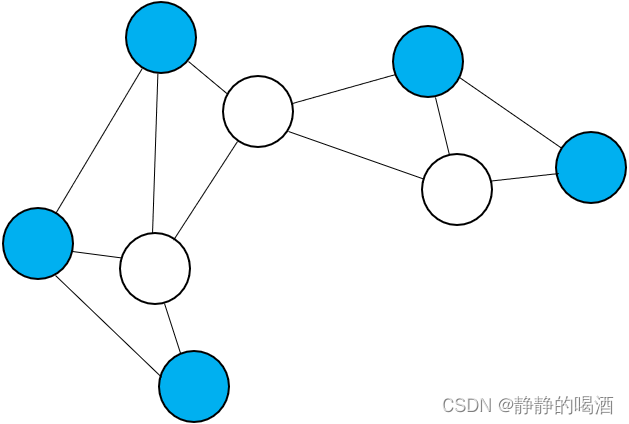
由于隐变量Z\mathcal ZZ、观测变量X\mathcal XX内部可能存在关联关系,因此关于该模型隐变量的后验概率P(Z∣X)\mathcal P(\mathcal Z \mid \mathcal X)P(Z∣X),干脆是无法用公式表达的。 -
还有一种就是以Sigmoid\text{Sigmoid}Sigmoid信念网络(Sigmoid Belief Network\text{Sigmoid Belief Network}Sigmoid Belief Network)为代表的包含隐变量、观测变量的贝叶斯网络:
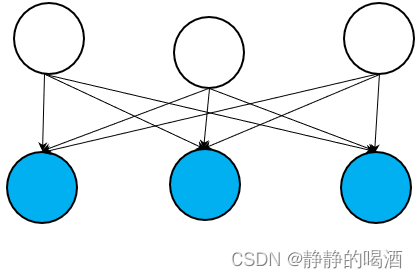
该模型同样无法对其联合概率分布P(X,Z)\mathcal P(\mathcal X,\mathcal Z)P(X,Z)进行分解,其核心原因是 指向同一观测变量的隐变量结点之间属于V\mathcal VV型结构。而V\mathcal VV型结构意味着隐变量结点之间不是相互独立的,因而无法分解。
关于V\mathcal VV型结构 -> 贝叶斯网络的条件独立性描述详见贝叶斯网络的结构表示,也称作Explain Away\text{Explain Away}Explain Away问题. -
最后一种情况就是上述两种情况的混合情况。代表模型是深度信念网络(Deep Belief Network,DBN\text{Deep Belief Network,DBN}Deep Belief Network,DBN),这里就不再赘述了。
由于受限玻尔兹曼机的条件约束,使得隐变量、观测变量内部均条件独立。但并不是说受限玻尔兹曼机比玻尔兹曼机性能更强大(powerful\text{powerful}powerful),而是玻尔兹曼机仅是理论上的产物,太过于理想化。在真实环境中没有实际作用;
相反受限玻尔兹曼机通过增加约束,使得隐变量的后验分布P(Z∣X)\mathcal P(\mathcal Z \mid \mathcal X)P(Z∣X)能够准确表示出来。相当于 放弃了模型复杂度,而去追求计算上的可行性。
与之相似的还有‘隐马尔可夫模型’中的齐次马尔可夫假设与观测独立性假设,它们都是放弃复杂度、追求计算可行性的典型示例。
可以看出,无向图模型无法直接表示后验概率的主要原因在于随机变量结点之间关联关系过于复杂,从而无法实现条件独立性;而有向图模型无法直接表示后验概率的主要原因在于随机变量之间的结构关系,从而无法实现条件独立性。
相关参考:
(系列二十五)近似推断1-介绍
相关文章:

机器学习笔记之近似推断(一)从深度学习角度认识推断
机器学习笔记之近似推断——从深度学习角度认识推断引言推断——基本介绍精确推断难的原因虽然能够表示,但计算代价太大无法直接表示引言 本节是一篇关于推断总结的博客,侧重点在于深度学习模型中的推断任务。 推断——基本介绍 推断(Inference\text{…...
指针的进阶
一、字符指针 int main() {char ch w;char* pc &ch;//pc就是字符指针//const char *p "abcdef";//这里其实是把字符串"abcdef"的首地址放入了指针p中//*p w;//这是错误的无法修改值(可以看到这里绿色波浪线警告)char arr[] …...

一元二次方程方程的类
1 问题设计一个一元二次方程的类,其中包括能够反映一元二次方程的属性与操作行为,然后再设计一个测试类,检测类的使用情况。2 方法使用package语句将方程的属性即计算跟的方法封装在一个有包名的类中,包名为tom.jiafei,…...

Ask林曦|来回答,30个你关心的日常问题(二)
在林曦老师的线上书法直播课上,上课前后的聊天时间里,时常有同学向林曦老师提问,这些问题涵盖了日常生活的诸多方面,从身体的保养,到快乐的法门,皆是大家感兴趣的,也都共同关切的。 暄桐教室…...

哪款电容笔适合开学季?电容笔和Apple Pencil的区别
其实,市场上一般的电容笔和Apple Pencil的最大差别,就在于Apple Pencil与普通电容笔两者的重量和压感。然而,由于苹果电容笔价格过高,目前电容笔的市场份额逐渐转向平替电容笔,平替电容笔其性能也逐渐得到改善。下面&a…...

Qt之Qprocess
QProcess 可用于完成启动外部程序,并与之交互通信。 一、启动外部程序的两种方式 1)一体式:void QProcess::start(const QString & program,const QStringList &arguments,OpenMode mode ReadWrite) 外部程序启动后&…...

为什么不愿意专升本 学历有什么用
专升本包括两种形式普通专升本和成人专升本。普通专升本毕业是全日制学历,考试仅有一次,错过不能补考所以考生不愿意选择,成人专升本毕业是非全日制学历,学历被国家承认,和普通高校毕业证有相同的使用效力。为何考生不…...

构造函数的使用大全
概述 在C中创建一个对象时,通常需要做一些数据初始化的工作,因此便提供了一个特殊的成员函数 —— 构造函数。一般情况下,并不需要程序员主动调用构造函数,而是在创建对象时,由系统自动调用。构造函数可以由程序员定义…...
ASP.NET Core MVC 项目 IOC容器
目录 一:什么是IOC容器 二:简单理解内置Ioc容器 三:依赖注入内置Ioc容器 四:生命周期 五:多种注册方式 一:什么是IOC容器 IOC容器是Inversion Of Control的缩写,翻译的意思就是控制反转。 …...

ARM工控机/网关- 钡铼技术
一、NXP处理器ARM控制器的介绍 NXP半导体是汽车、穿戴、消费电子等领域中智能机器解决方案的领先供应商。其产品线庞大,包括处理器、微控制器、快速设计平台、ARM控制器等。在物联网控制、汽车电子、安全应用等领域,NXP处理器ARM控制器已成为半导体行业的…...
为什么都在喊数据可视化?它究竟怎么做?
在数字化转型的浪潮中,不论是传统行业,还是新兴行业总会提到“数据可视化”这个词。那数据可视化到底是什么?为什么会受到那么多人追捧?又该怎么才能做到数据可视化呢? 一、数据可视化是什么? 首先“可视…...
nodejs+vue停车场停车位短租系统vscode
目 录前端技术:nodejsvueelementui 前端:HTML5,CSS3、JavaScript、VUE 1、 node_modules文件夹(有npn install产生) 这文件夹就是在创建完项目后,cd到项目目录执行npm install后生成的文件夹,下载了项目需要的依赖项。 2、…...

物理真机上LUKS结合TPM的测试 —— 使用随机数密钥
1. 创建磁盘空间 命令如下: dd if/dev/zero ofenc.disk bs1M count50 实际命令及结果如下: $ dd if/dev/zero ofenc.disk bs1M count50 输入了 500 块记录 输出了 500 块记录 52428800 字节 (52 MB, 50 MiB) 已复制,0.0587495 sÿ…...
Linux USB 开发指南
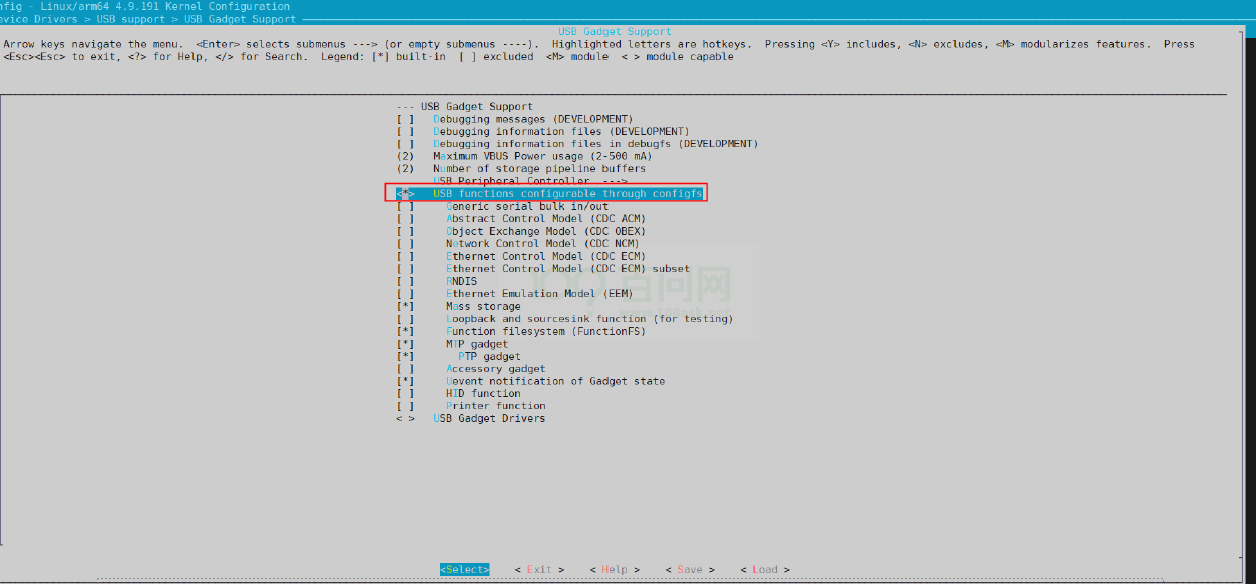
文章目录Linux USB 开发指南1 前言1.1 文档简介1.2 目标读者1.3 适用范围2 模块介绍2.1 模块功能介绍2.2 相关术语介绍2.3 模块配置介绍2.3.1 Device Tree 配置说明2.3.2 board.dts 配置说明2.3.3 kernel menuconfig 配置说明2.4 源码结构介绍2.5 驱动框架介绍2.6 Gadget 配置2…...

FreeRTOS入门(03):队列、信号量、互斥量
文章目录目的队列(queue)信号量(semaphore)互斥量(mutex)互斥量递归互斥量总结目的 FreeRTOS提供给用户最核心的功能是任务(Task),实际项目中通常会有多个任务ÿ…...
Biome-BGC在模拟过程中,如何使用Linux、Python等,完成前处理和后处理工作???
在Biome-BGC模型中,对于碳的生物量积累,采用光合酶促反应机理模型计算出每天的初级生产力(GPP),将生长呼吸和维持呼吸减去后的产物分配给叶、枝条、干和根。生物体的碳每天都按一定比例以凋落方式进入凋落物碳库;对于水份输运过程…...
【unittest学习】unittest框架主要功能
1.认识unittest在 Python 中有诸多单元测试框架,如 doctest、unittest、pytest、nose 等,Python 2.1 及其以后的版本已经将 unittest 作为一个标准模块放入 Python 开发包中。2.认识单元测试不用单元测试框架能写单元测试吗?答案是肯定的。单…...
京东测开岗3+1面经+经验分享,拿到offer,月薪34k....
现在,招聘黄金时间已经来临,在网上看了很多大佬的面经,也加了很多交流群,受到了很多朋友的提点,今天终于轮到我来分享面经啦,之前面试了几家公司,最后拿到了京东测试岗的 offer,这里…...
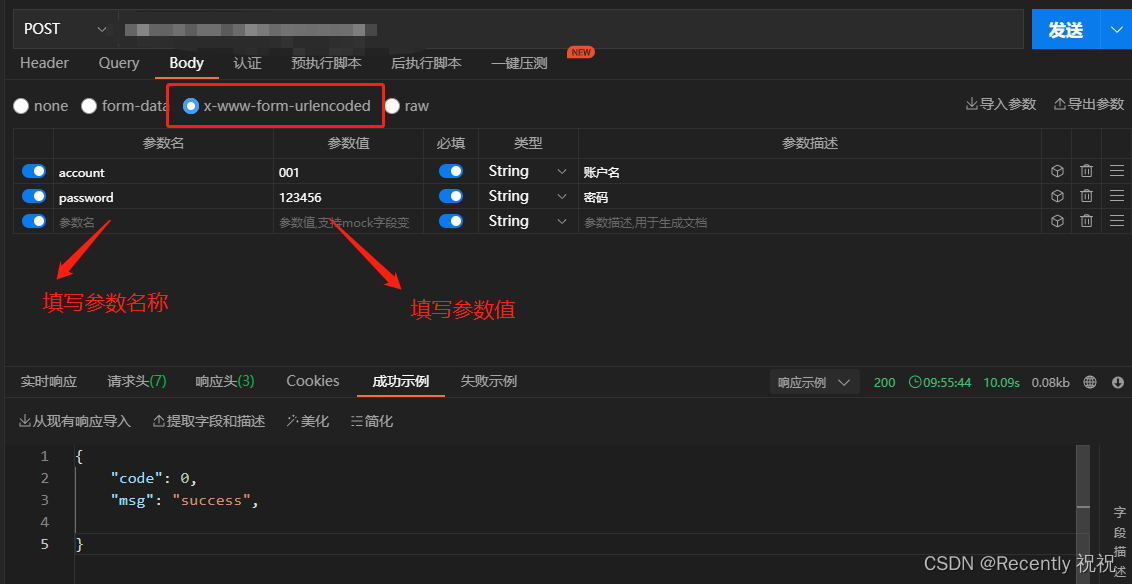
后端接收格式为x-www-form-urlencoded的数据
1.x-www-form-urlencoded是什么? x-www-form-urlencoded纸面翻译即所谓url格式的编码,是post的默认Content-Type,其实就是一种编码格式,类似json也是一种编码传输格式。form表单中使用 form的enctype属性为编码方式࿰…...
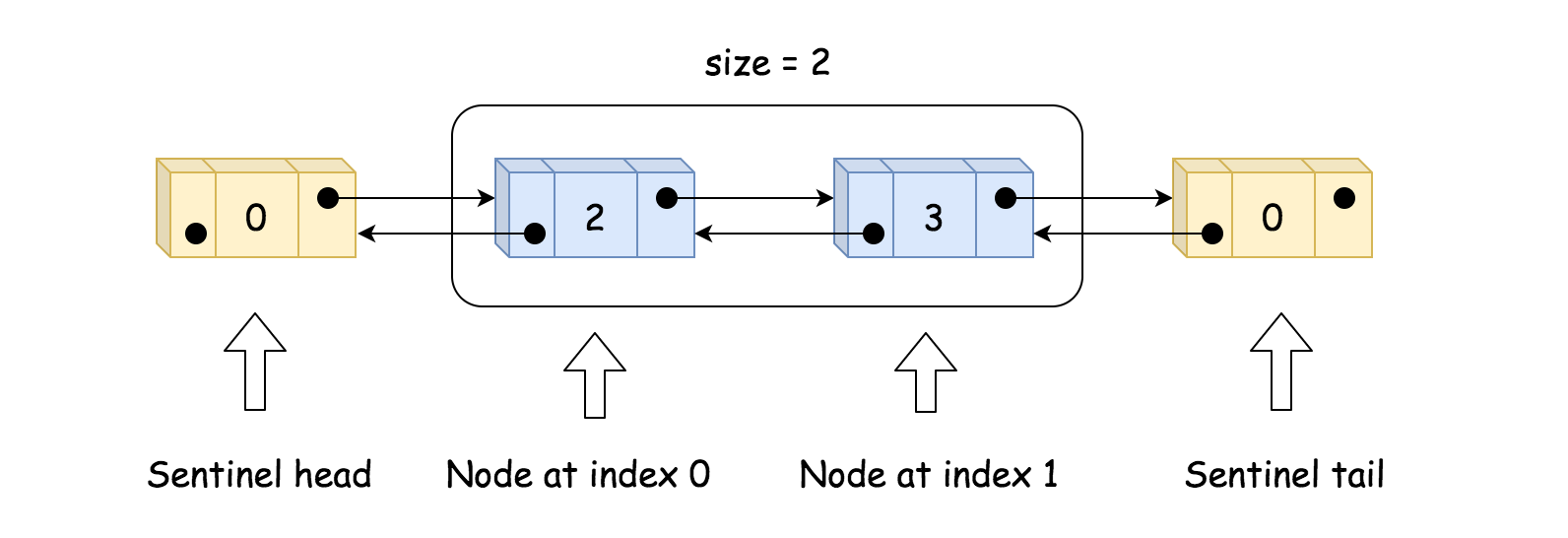
LeetCode 707. 设计链表
LeetCode 707. 设计链表 难度:middle\color{orange}{middle}middle 题目描述 设计链表的实现。您可以选择使用单链表或双链表。单链表中的节点应该具有两个属性:valvalval 和 nextnextnext。valvalval 是当前节点的值,nextnextnext 是指向下…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...

ETLCloud可能遇到的问题有哪些?常见坑位解析
数据集成平台ETLCloud,主要用于支持数据的抽取(Extract)、转换(Transform)和加载(Load)过程。提供了一个简洁直观的界面,以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...

第7篇:中间件全链路监控与 SQL 性能分析实践
7.1 章节导读 在构建数据库中间件的过程中,可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中,必须做到: 🔍 追踪每一条 SQL 的生命周期(从入口到数据库执行)&#…...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...
