【华为OD机试模拟题】用 C++ 实现 - 非严格递增连续数字序列(2023.Q1)
相关文章:

【华为OD机试模拟题】用 C++ 实现 - 非严格递增连续数字序列(2023.Q1)
最近更新的博客 华为OD机试 - 入栈出栈(C++) | 附带编码思路 【2023】 华为OD机试 - 箱子之形摆放(C++) | 附带编码思路 【2023】 华为OD机试 - 简易内存池 2(C++) | 附带编码思路 【2023】 华为OD机试 - 第 N 个排列(C++) | 附带编码思路 【2023】 华为OD机试 - 考古…...

RN面试题
RN面试题1.React Native相对于原生的ios和Android有哪些优势?1.性能媲美原生APP 2.使用JavaScript编码,只要学习这一种语言 3.绝大部分代码安卓和IOS都能共用 4.组件式开发,代码重用性很高 5.跟编写网页一般,修改代码后即可自动刷…...
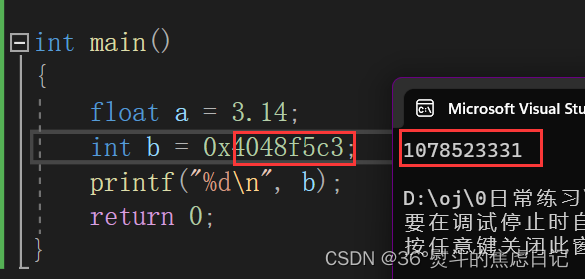
【数据存储】浮点型在内存中的存储
目录 一、存储现象 二、IEEE标准规范 1.存储 2.读取 三、举例验证 1.存储 2.读取 浮点型存储的标准是IEEE(电气电子工程师学会)754制定的。 一、存储现象 浮点数由于其有小数点的特殊性,有很多浮点数是不能精确存储的,如&#…...
:异常处理)
Servlet笔记(8):异常处理
1、错误页面配置 web.xml <!-- servlet 定义 --> <servlet><servlet-name>ErrorHandler</servlet-name><servlet-class>ErrorHandler</servlet-class> </servlet> <!-- servlet 映射 --> <servlet-mapping><servle…...

stm32f407探索者开发板(二十一)——窗口看门狗
文章目录一、窗口看门狗概述1.1 看门狗框图1.2 窗口看门狗工作过程总结1.3 超时时间1.4 为什么需要窗口看门狗1.5 其他注意事项二、常用寄存器和库函数2.1 控制寄存器WWDG_ CR2.2 配置寄存器WWDG_ CFR2.3 状态寄存器WWDG_SR三、手写窗口看门狗3.1 配置过程3.2 初始化窗口看门狗…...
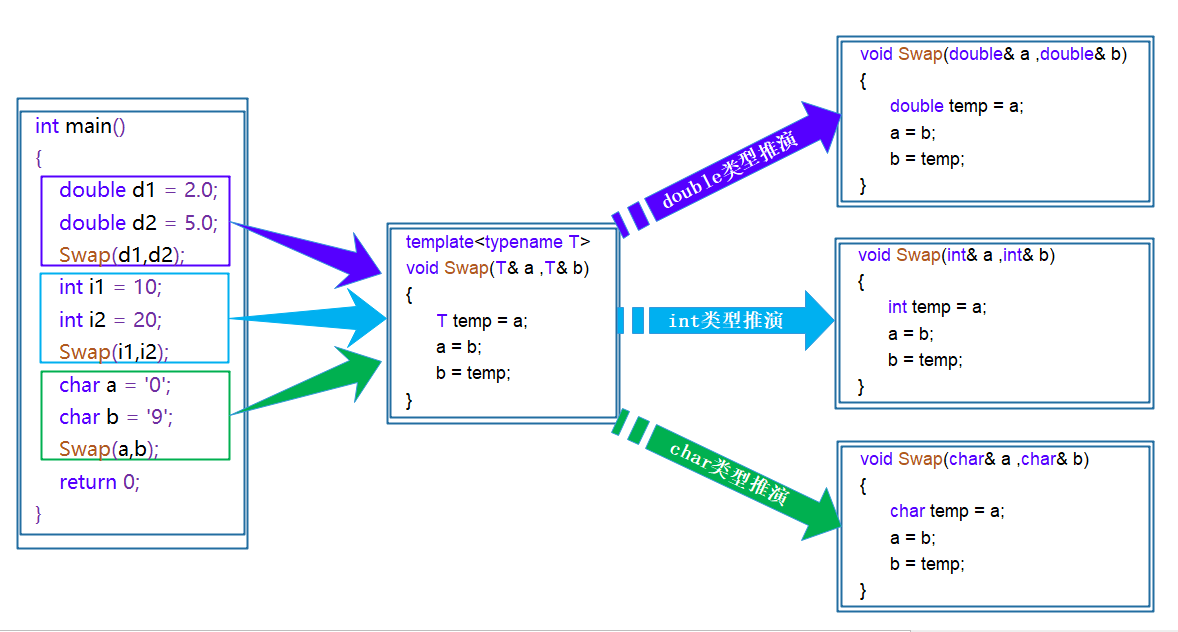
C++ 模板
1. 泛型编程实现一个通用的交换函数,使用函数重载虽然可以实现,但是有以 下几个不好的地方:1. 重载的函数仅仅是类型不同,代码复用率比较低,只要有新类型出现时,就需要用户自己增加对应的函数2. 代码的可维…...

C++中的友元及运算符重载
友元 意义 程序中,有些私有属性也想让类外特殊的一些函数或者类进行访问,就要用到友元技术 关键字 friend 友元的三种实现 全局函数做友元 class Room{friend void test(Person &p);//friend class test;public:string phone_number;private:string…...
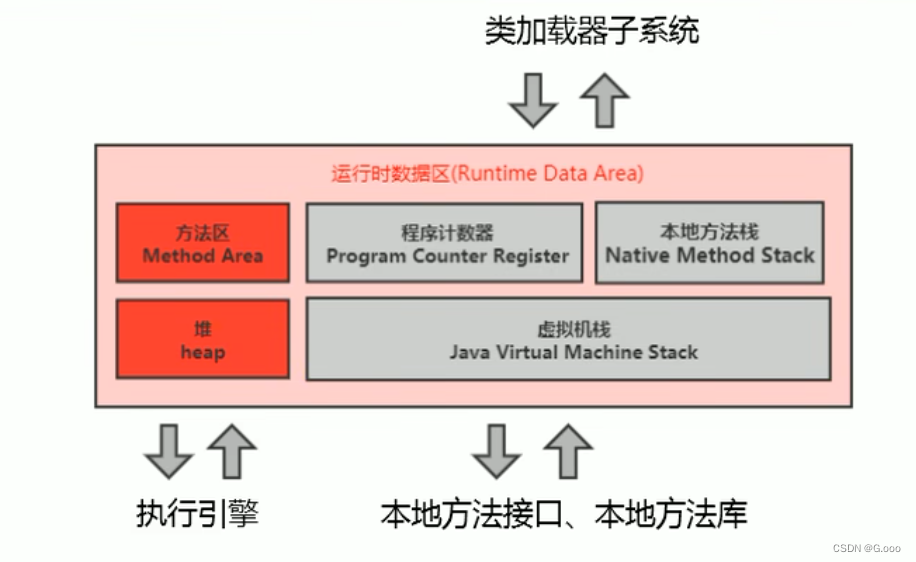
五、运行时数据区内部结构、JVM中的线程
内存是非常重要的系统资源,是硬盘和cpu的中间仓库及桥梁,承载着操作系统和应用程序的实时运行。JVM内存布局规定了Java在运行过程种内存申请、分配‘、管理的策略,保证了JVM的高效稳定运行,不同的JVM对于内存的划分方式和管理机制…...
Codeforces Round #848 (Div. 2)A-C
传送门 目录 A. Flip Flop Sum 代码: B. The Forbidden Permutation 代码: C. Flexible String 代码: A. Flip Flop Sum 题意:给你一个长度为n的数组(数组元素只为1或者-1),你要且只能进行…...
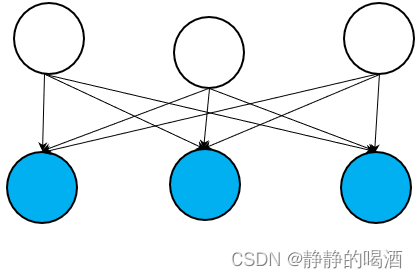
机器学习笔记之近似推断(一)从深度学习角度认识推断
机器学习笔记之近似推断——从深度学习角度认识推断引言推断——基本介绍精确推断难的原因虽然能够表示,但计算代价太大无法直接表示引言 本节是一篇关于推断总结的博客,侧重点在于深度学习模型中的推断任务。 推断——基本介绍 推断(Inference\text{…...
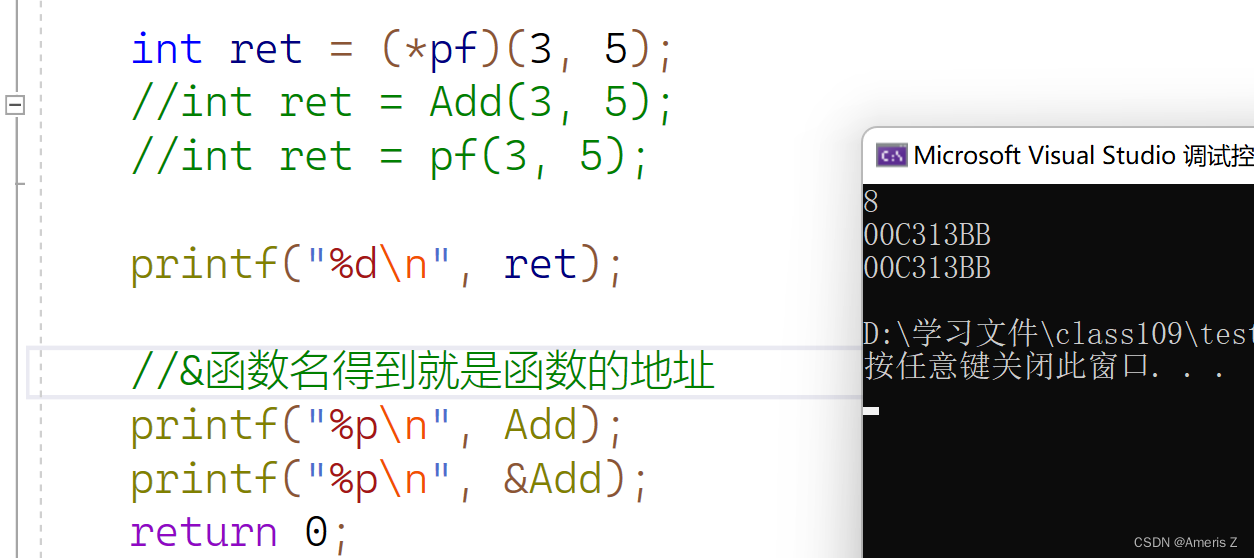
指针的进阶
一、字符指针 int main() {char ch w;char* pc &ch;//pc就是字符指针//const char *p "abcdef";//这里其实是把字符串"abcdef"的首地址放入了指针p中//*p w;//这是错误的无法修改值(可以看到这里绿色波浪线警告)char arr[] …...

一元二次方程方程的类
1 问题设计一个一元二次方程的类,其中包括能够反映一元二次方程的属性与操作行为,然后再设计一个测试类,检测类的使用情况。2 方法使用package语句将方程的属性即计算跟的方法封装在一个有包名的类中,包名为tom.jiafei,…...

Ask林曦|来回答,30个你关心的日常问题(二)
在林曦老师的线上书法直播课上,上课前后的聊天时间里,时常有同学向林曦老师提问,这些问题涵盖了日常生活的诸多方面,从身体的保养,到快乐的法门,皆是大家感兴趣的,也都共同关切的。 暄桐教室…...

哪款电容笔适合开学季?电容笔和Apple Pencil的区别
其实,市场上一般的电容笔和Apple Pencil的最大差别,就在于Apple Pencil与普通电容笔两者的重量和压感。然而,由于苹果电容笔价格过高,目前电容笔的市场份额逐渐转向平替电容笔,平替电容笔其性能也逐渐得到改善。下面&a…...

Qt之Qprocess
QProcess 可用于完成启动外部程序,并与之交互通信。 一、启动外部程序的两种方式 1)一体式:void QProcess::start(const QString & program,const QStringList &arguments,OpenMode mode ReadWrite) 外部程序启动后&…...

为什么不愿意专升本 学历有什么用
专升本包括两种形式普通专升本和成人专升本。普通专升本毕业是全日制学历,考试仅有一次,错过不能补考所以考生不愿意选择,成人专升本毕业是非全日制学历,学历被国家承认,和普通高校毕业证有相同的使用效力。为何考生不…...

构造函数的使用大全
概述 在C中创建一个对象时,通常需要做一些数据初始化的工作,因此便提供了一个特殊的成员函数 —— 构造函数。一般情况下,并不需要程序员主动调用构造函数,而是在创建对象时,由系统自动调用。构造函数可以由程序员定义…...
ASP.NET Core MVC 项目 IOC容器
目录 一:什么是IOC容器 二:简单理解内置Ioc容器 三:依赖注入内置Ioc容器 四:生命周期 五:多种注册方式 一:什么是IOC容器 IOC容器是Inversion Of Control的缩写,翻译的意思就是控制反转。 …...

ARM工控机/网关- 钡铼技术
一、NXP处理器ARM控制器的介绍 NXP半导体是汽车、穿戴、消费电子等领域中智能机器解决方案的领先供应商。其产品线庞大,包括处理器、微控制器、快速设计平台、ARM控制器等。在物联网控制、汽车电子、安全应用等领域,NXP处理器ARM控制器已成为半导体行业的…...
为什么都在喊数据可视化?它究竟怎么做?
在数字化转型的浪潮中,不论是传统行业,还是新兴行业总会提到“数据可视化”这个词。那数据可视化到底是什么?为什么会受到那么多人追捧?又该怎么才能做到数据可视化呢? 一、数据可视化是什么? 首先“可视…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

【分享】推荐一些办公小工具
1、PDF 在线转换 https://smallpdf.com/cn/pdf-tools 推荐理由:大部分的转换软件需要收费,要么功能不齐全,而开会员又用不了几次浪费钱,借用别人的又不安全。 这个网站它不需要登录或下载安装。而且提供的免费功能就能满足日常…...

tomcat入门
1 tomcat 是什么 apache开发的web服务器可以为java web程序提供运行环境tomcat是一款高效,稳定,易于使用的web服务器tomcathttp服务器Servlet服务器 2 tomcat 目录介绍 -bin #存放tomcat的脚本 -conf #存放tomcat的配置文件 ---catalina.policy #to…...

pikachu靶场通关笔记19 SQL注入02-字符型注入(GET)
目录 一、SQL注入 二、字符型SQL注入 三、字符型注入与数字型注入 四、源码分析 五、渗透实战 1、渗透准备 2、SQL注入探测 (1)输入单引号 (2)万能注入语句 3、获取回显列orderby 4、获取数据库名database 5、获取表名…...
