数据结构——排序算法(C语言)
本篇将详细讲一下以下排序算法:
- 直接插入排序
- 希尔排序
- 选择排序
- 快速排序
- 归并排序
- 计数排序
排序的概念
排序:所谓排序,就是使一串记录,按照其中的某个或某写关键字的大小,按照递增或递减0排列起来的操作。
稳定性的概念
假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变。如一下例子,
5 2 3 4 5 9 8
经过排序,如果红5和蓝5的相对顺序不对,这就叫稳定,反之则不稳定。
直接插入排序
直接插入排序的思想:将待排序的记录按其关键码值的大小逐个插入到一个已经排好序的序列中,直到所有的序列为有序序列。
实际中,我们玩扑克牌时,就用到了这样的一个排序算法。



时间复杂度:
直接插入排序时一个稳定的排序,如果有相同的元素,它们的相对位置不会发生变化。它时间复杂度最好的情况下是O(N),当一个数插入到已经排好序的序列中,只需要比较一次就好了。
最坏情况:O(N^2) ,在完全逆序的情况下,要排升序。
希尔排序
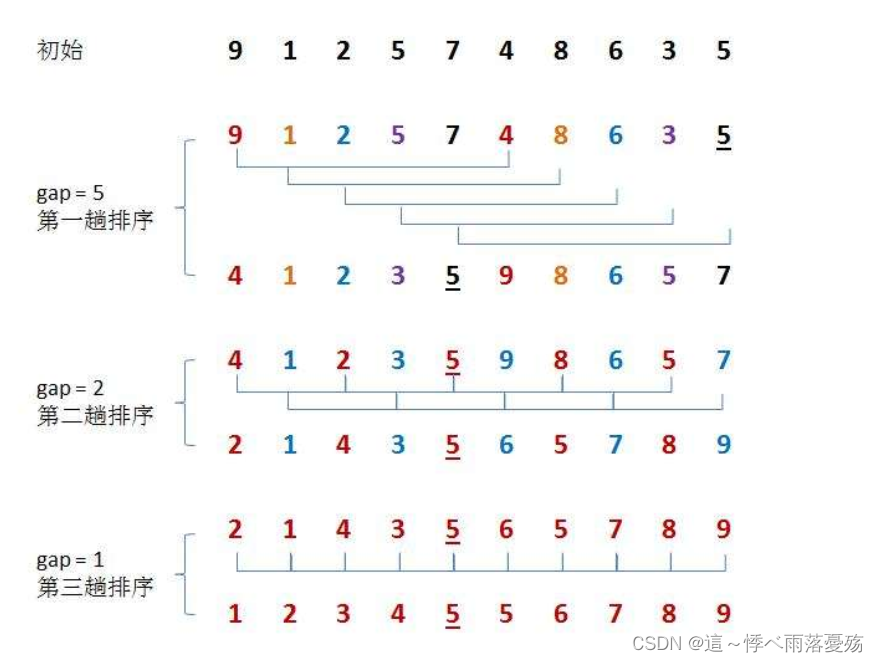
希尔排序其实和插入排序很像,只不过希尔排序的思想是:先预排序,最后插入排序。
预排序的意义在哪里??
- 大的数更快到后面去,小的数更快到前面去。gap越大跳的越快,越不有序,当gap =1 时就是插入排序。

时间复杂度
希尔排序的时间复杂度:大约为O(N^1.3)
选择排序
选择排序的思想:选择排序可以在一次查找中找到最大的数和最小的数,然后把最大的数放到最后,最小的数放到最前面。

时间复杂度
时间复杂度是O(N^2)
稳定性:差

快速排序
快排思想:说到排序,或多或少都听过快速排序,快速排序是Hoare于1962年提出的一种二叉树结构的交换方法,其基本思想为:任取待排序元素序列中的某个元素作为基准值,按照该排序吗将待排序集合分割成2个子序列,左序列小于keyi值,右序列大于keyi值,然后重复此方法,最后拍完序。
快速排序一次可以确定一个值在正确的位置上。(这个值就是key值)
if (begin >= end){return;}int left = begin, right = end;int keyi = left;while (left < right){//先让右边先走while (left<right && a[right]>=a[keyi]){--right;}while (left < right && a[left] <= a[keyi]){++left;}Swap(&a[left], &a[right]);}Swap(&a[keyi], &a[left]);keyi = left;//[begin,keyi-1] keyi [keyi+1,end]QuickSort(a,begin,keyi-1);QuickSort(a,keyi+1,end);最常见的就是上面的递归代码,这是Hoare的一种方式实现快排。
Hoare思想:让基准值的右边先走,直到找到比基准值小的数,然后让左边走,直到找到比基准值大的数,然后交换,最后left=right相等的时候,将left位置的值与基准值交换。这样就实现了一次排序。

这里我们想一想快速排序为什么要让基准值的对面开始????

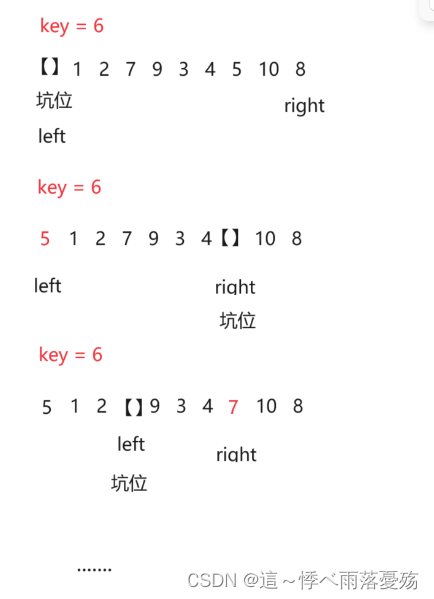
挖坑法: 用一个tmp记录第一个值的坑位,让右边先走,直到找到比坑位小的数,然后让a[right]赋值给坑位,然后把坑位给给right,继续让左边先走,直到找到比坑位大的数,然后把值赋给坑位,让坑位给给left,一直循环。
前后指针法:让prev指向key值,cur指向key值之后的一个值,当a[cur] < a[key] 的时候,就让prev++和cur交换,然后一直循环。

快排的非递归: 快排的思想其实不难发现像一个栈(后进先出),因为快排每次可以确定一个基准值的位置,所以,第一次push进left和right,让他们进行一次排序,就接着push进right和keyi+1,再push进keyi-1和left,注意顺序,因为快排的中间也是一个后进先出的思想。
快排的缺点
快排其实是有缺点的,因为快排的时间复杂度不一定是O(N*logN),如果排升序,给一个倒序的序列,就有可能达到O(N^2)。所以有了这么一个缺点,就可以做一个三数区中的优化,其实Sort函数中也有这样的处理,而且Sort中还优化了一次快排递归深度过深的时候会用堆排序,在接近有序的时候会用插入排序,而且Sort中只对了右边进行递归处理。如果有兴趣,可以去了解一下Sort的源码,里面有详细解释。

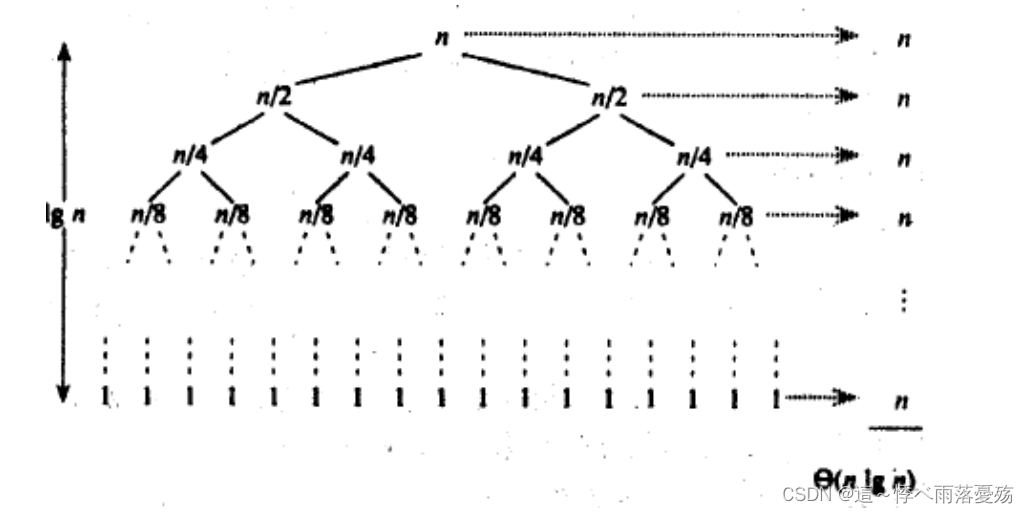
归并排序
归并排序:它是建立在归并操作上的一种有效的排序算法,该算法采用了分治的思想。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段有序。若将两个有序表合并成一个有序表,称为二路归并。
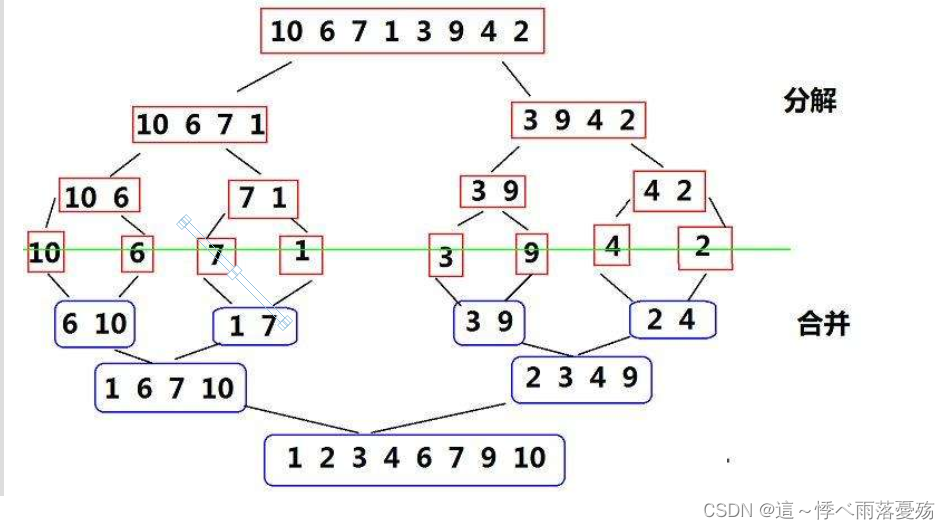

归并排序可以看出是一个后序的排序, 先递归,然后从前面开始排好序,然后再memcpy到原数组。
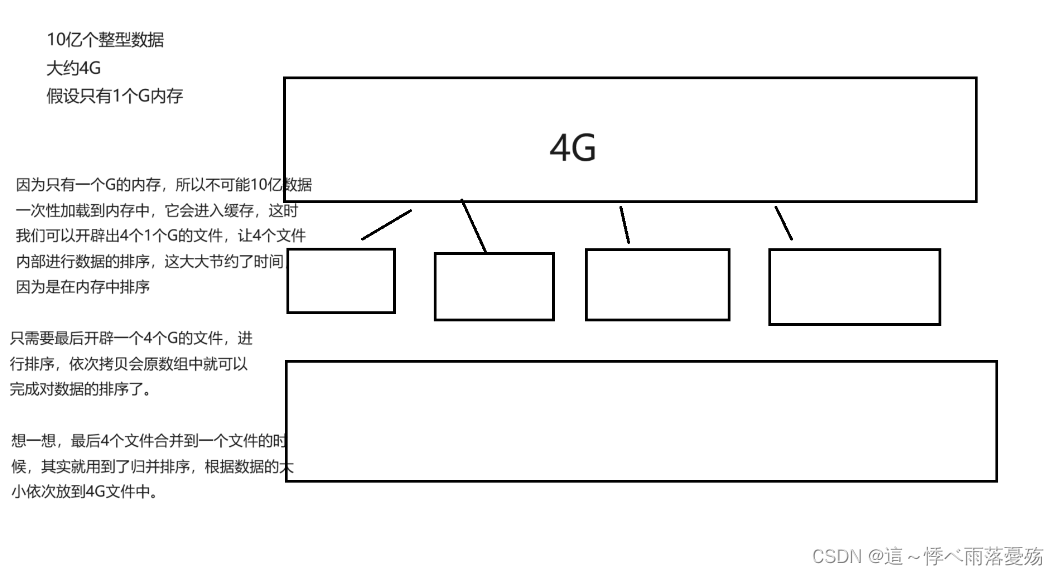
归并排序其实用在解决磁盘外的外排序问题中,如果有下面的场景,归并排序就起到了很大的作用。
时间复杂度
归并排序也是一种经典的O(N*logN) 空间复杂度是O(N),这时因为开辟了一块tmp临时数组
计数排序
思想:计数排序又称为鸽巢原理,是对哈希直接定址法的变形应用。
步骤:1.统计想相同元素出现的次数
2.根据统计的结果将序列回收到原来的序列中
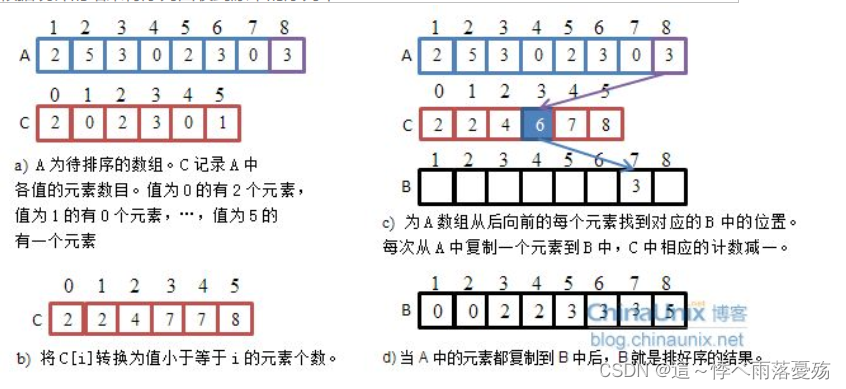 计数排序的特性:
计数排序的特性:
- 计数排序在数据范围集中时,效率很高,但是使用范围及场景有限。
- 时间复杂度:O(MAX(N,范围))
- 空间复杂度:O(范围)
相关文章:

数据结构——排序算法(C语言)
本篇将详细讲一下以下排序算法: 直接插入排序希尔排序选择排序快速排序归并排序计数排序 排序的概念 排序:所谓排序,就是使一串记录,按照其中的某个或某写关键字的大小,按照递增或递减0排列起来的操作。 稳定性的概念…...

基于Http Basic Authentication的接口
Basic Authenrication是 HTTP 用户代理提供用户名的一种方法 ,它是对 Web 资源实施访问控制的最简单技术,它不需要 Cookie、会话标识符和登录页面。HTTP Basic身份验证使用静态的标准HTTP标头,这意味着 不必在预期中进行握手。 当用户代理想…...
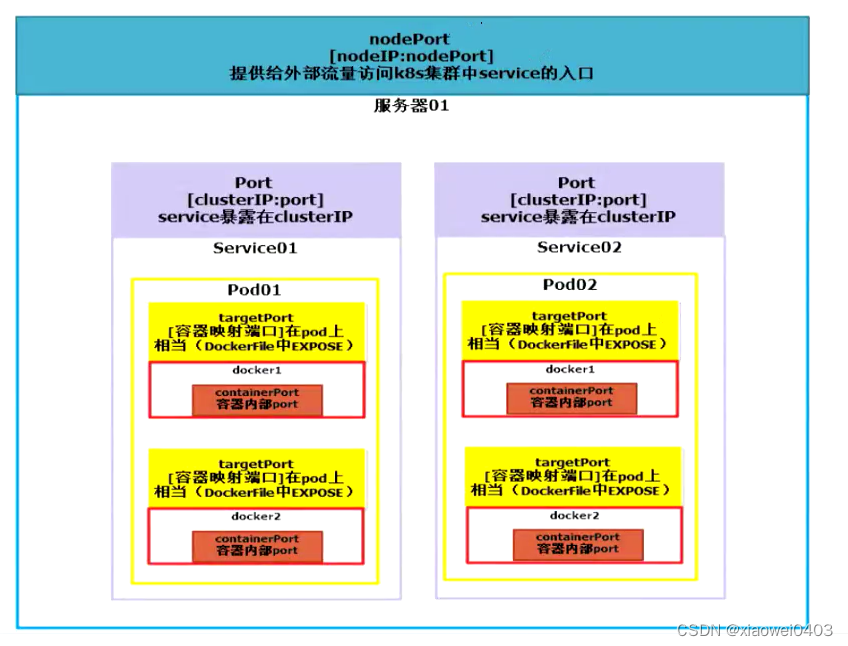
【yaml文件的编写】
yaml文件编写 YAML语法格式写一个yaml文件demo创建资源对象查看创建的pod资源创建service服务对外提供访问并测试创建资源对象查看创建的service在浏览器输入 nodeIP:nodePort 即可访问 详解k8s中的port:portnodePorttargetPortcontainerPortkubectl run --dry-runc…...
kt6368A双模蓝牙芯片无法透传 可能是什么问题呢
一、问题简介- kt6368A蓝牙芯片无法透传 可能是什么问题呢? KT6368A蓝牙芯片,在使用上还是非常的简单,总共也就8个腿,焊接也是很容易的事情 出现不能透传,大概率有如下2点原因 硬件问题,比如࿱…...
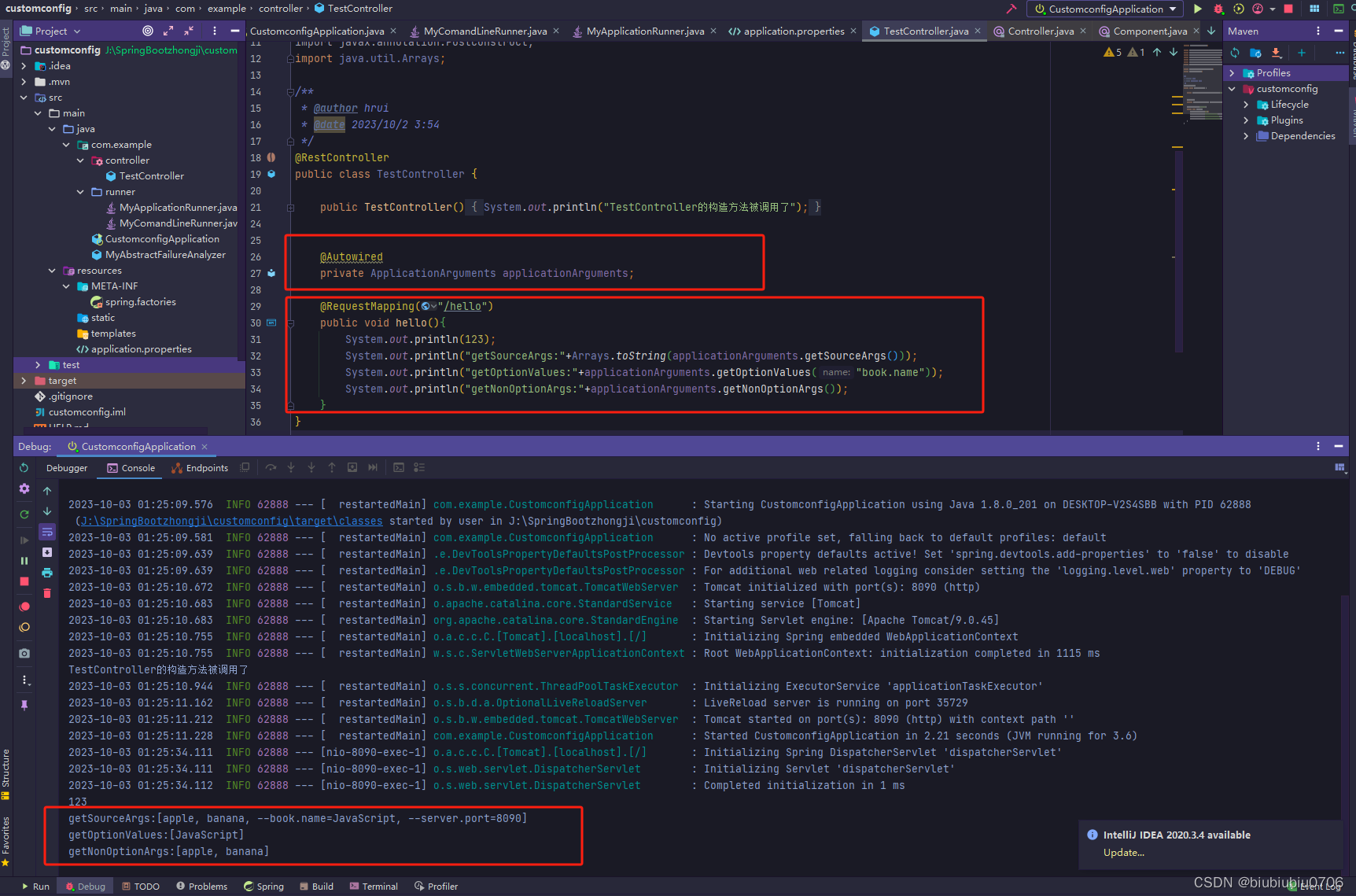
SpringBoot终极讲义第二章笔记
01.关于Import 和 ImportResource Import注解用法(类上): 一般和Configuration一起使用,用来导入里面Bean方法返回的对象 ImportResource(类上):一般和Configuration一起使用,用来导入某个.XML文件里的bean 个人觉得这两个注解有点鸡肋 SpringBoot启动类默认扫描的是启动类…...

【C++面向对象侯捷下】4. pointer-like classes,关于智能指针 | 5. function-like classes,所谓仿函数
文章目录 4. pointer-like classes,关于智能指针pointer-like classes,关于智能指针 shared_ptrpointer-like classes,关于迭代器5. function-like classes,所谓仿函数【不懂,跳过】 4. pointer-like classes,关于智能指针 pointer-like classes,关于智…...

社科院与杜兰大学能源管理硕士项目——惊喜会随时间慢慢酝酿而出
我们越来越难感受到惊喜,按部就班的生活让我们丧失了感知力,我们再难以被简单的确幸所打动。试试停下脚步,惊喜往往不期而遇。社科院与杜兰大学能源管理硕士项目是你人生中的小确幸吗 学习是一种持续不断的自我提升,它能让我们逐渐…...

Array简介
概念: 数组(Array)是Java中最简单的数据结构之一,它用于存储固定大小的相同类型元素序列。数组是一个连续分配的内存块,可以通过索引访问其中的元素。元素在数组中按照顺序排列,并使用整数索引来唯一标识每…...
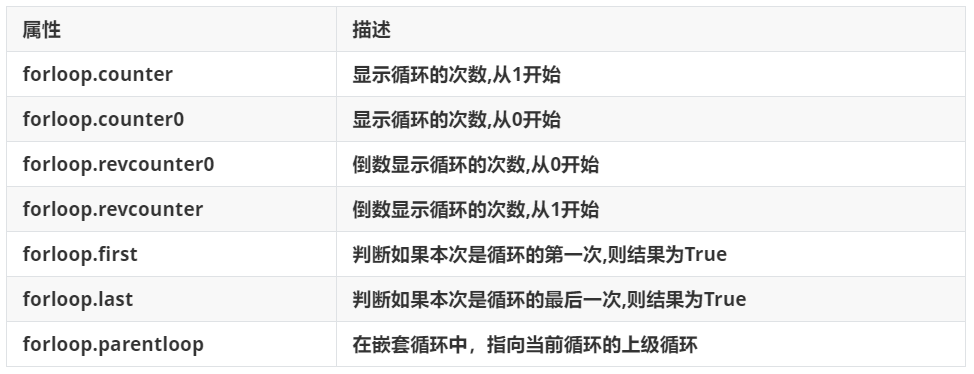
Django的模版使用(Django-03)
一 模版的使用 模板引擎是一种可以让开发者把服务端数据填充到html网页中完成渲染效果的技术。它实现了 把前端代码和服务端代码分离 的作用,让项目中的业务逻辑代码和数据表现代码分离,让前端开发者和服务端开发者可以更好的完成协同开发。 静态网页&…...
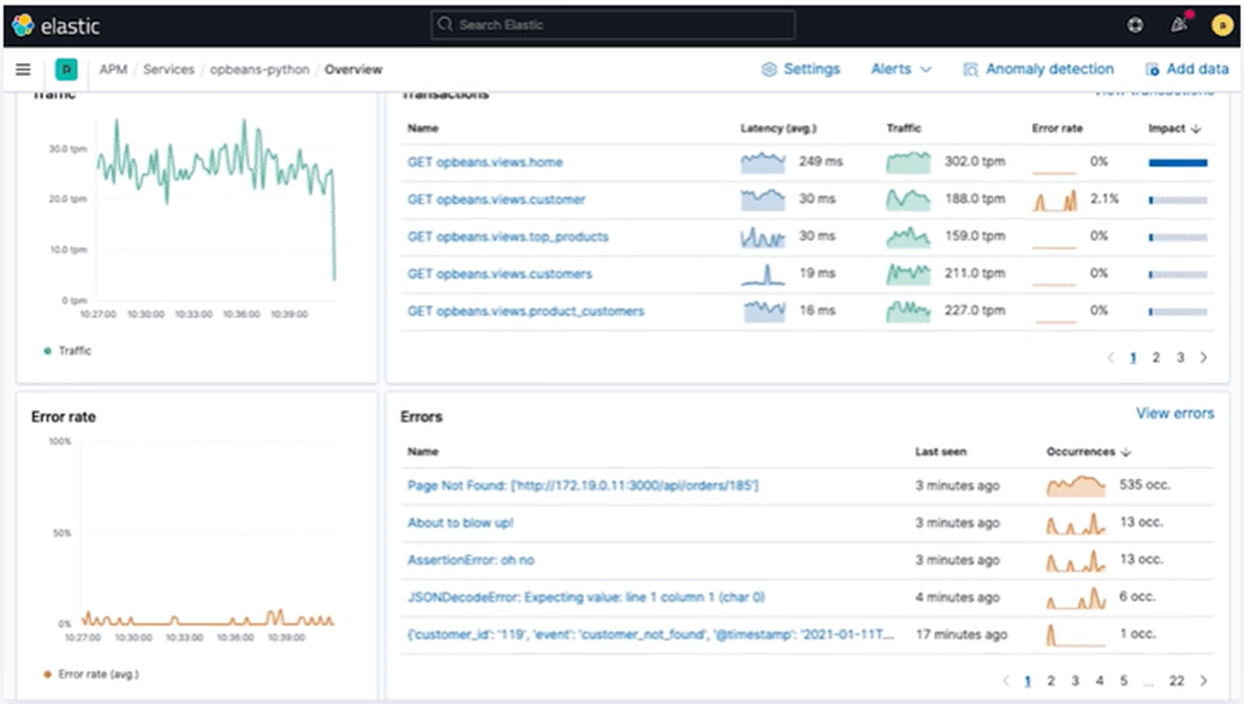
详解分布式搜索技术之elasticsearch
目录 一、初识elasticsearch 1.1什么是elasticsearch 1.2elasticsearch的发展 1.3为什么学习elasticsearch? 1.4正向索引和倒排索引 1.4.1传统数据库采用正向索引 1.4.2elasticsearch采用倒排索引 1.4.3posting list 1.4.4总结 1.5 es的一些概念 1.5.1文档和字段 …...

系统架构设计:3 软件架构建模技术与应用
目录 一 架构“4+1”视图 二 论点 1 架构的本质 2 “4+1”视图 (1)逻辑视图 <...
JAVA在线电子病历编辑器源码 B/S架构
电子病历在线制作、管理和使用的一体化电子病历解决方案,通过一体化的设计,提供对住院病人的电子病历书写、保存、修改、打印等功能。电子病历系统将临床医护需要的诊疗资料以符合临床思维的方法展示。建立以病人为中心,以临床诊疗信息为主线…...

TS中的枚举是什么如何使用
在 TypeScript 中,枚举(enum)是一种用于定义命名常量集合的数据类型。枚举可以提高代码的可读性和可维护性,因为它允许开发人员定义并使用有意义的符号名称来表示特定的常量。 下面是一个使用枚举的示例: enum Color…...
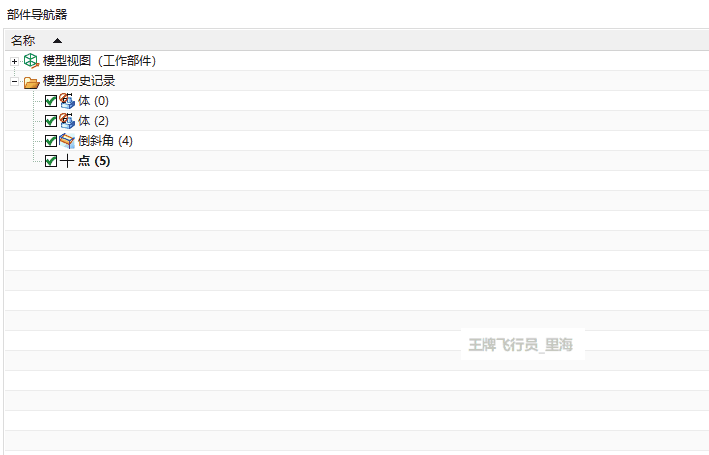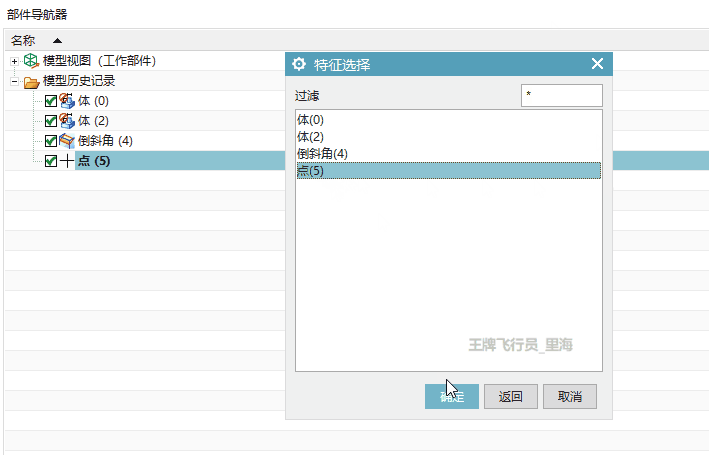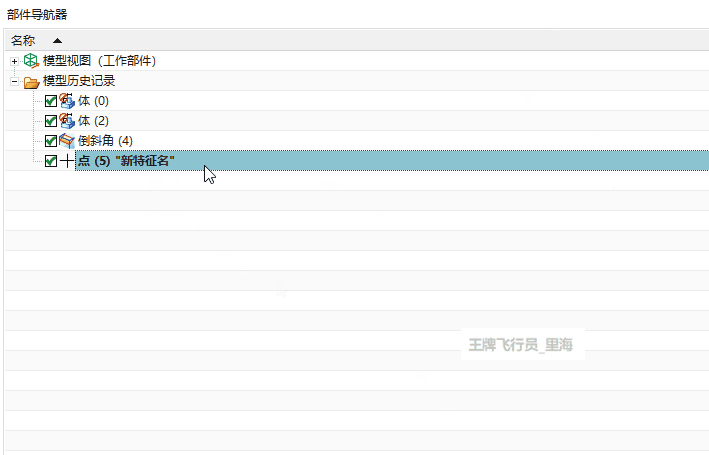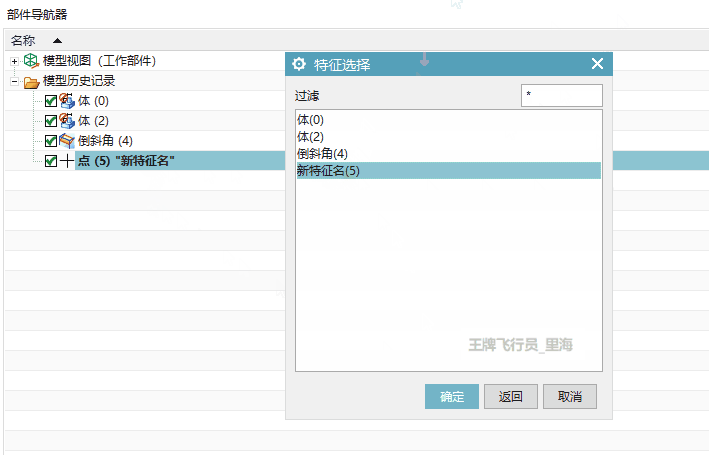
UG\NX二次开发 重命名特征对象 UF_OBJ_set_name
文章作者:里海 来源网站:《里海NX二次开发3000例专栏》 感谢粉丝订阅 感谢 林闹 订阅本专栏,非常感谢。 简介 UG\NX二次开发 重命名特征 UF_OBJ_set_name 效果 代码 #include "me.hpp" #include <vector> #include...

低欲望社会:只要我没欲望,世界就对我束手无策?
新的转变正在发生,越来越多的人,正从外部的物质世界向内部的精神世界回归。 比如,中产不再炫名牌,而是改炫读书;打工人不再炫工资,而是炫如何整顿职场。 越来越多的人认为消费主义弥漫着恶臭,…...
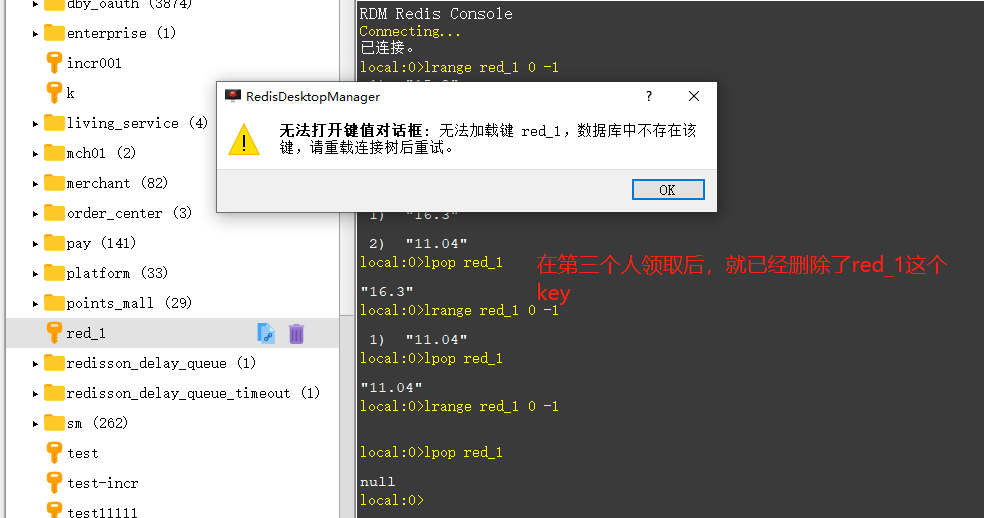
抢红包设计
抢红包大致可以分为2步:1 发红包 ;2 抢红包 发红包流程 为了突出红包设计主题,以下设计会忽略支付流程、24H过期退款剩余金额、用户领取红包余额到账等业务,则简化后的相关表设计如下: CREATE TABLE red_record (id…...

k8s集群-6(daemonset job cronjob控制器)
Daemonset 一个节点部署一个节点 当有节点DaemonSet 确保全部 (或者某些) 节点上运行一个 Pod 的副本。加入集群时,也会为他们新增一个 Pod 。当有节点从集群移除时,这些Pod 也会被回收。删除 DaemonSet 将会删除它创建的所有 Pod。 DaemonSet 的典型用…...

Compose 编译器版本和Kotlin版本对应关系
使用了最新的kotlin版本,compose报错,不兼容,在这里记录一下版本对应关系 值得注意的是Compose Kotlin 编译器扩展 (androidx.compose.compiler) 未关联到 Compose 库版本。相反,它会关联到 Kotlin 编译器插件的版本,…...

vite+vue+cesium
1.创建vite项目 npm create vite 项目名称 2. 选择vuejs/ts 3.在终端输入命令 npm install 4.安装cesium插件,在终端输入命令 npm i cesium vite-plugin-cesium vite -D 5.项目配置cesium 在vite.config.js里进行配置 import { defineConfig } from vite i…...
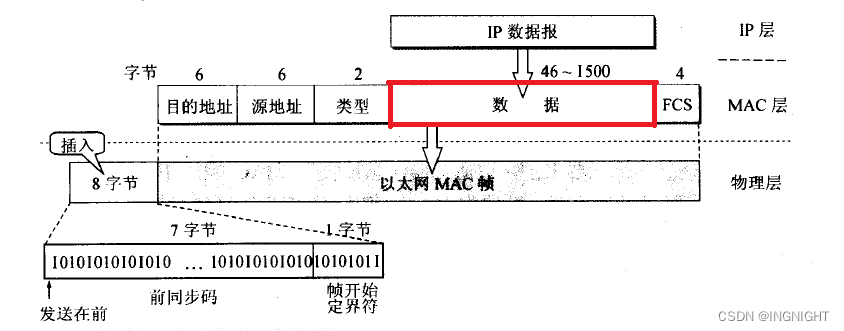
tcp滑动窗口原理
18.1 滑动窗口 我们再来看这个比喻: 网络仅仅是保证了整个网络的连通性,我们我们基于整个网络去传输,那么是不是我想发送多少数据就发送多少数据呢?如果是这样的话,是不是就会像我们的从一个池塘抽水去灌到另外一个…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...

Webpack性能优化:构建速度与体积优化策略
一、构建速度优化 1、升级Webpack和Node.js 优化效果:Webpack 4比Webpack 3构建时间降低60%-98%。原因: V8引擎优化(for of替代forEach、Map/Set替代Object)。默认使用更快的md4哈希算法。AST直接从Loa…...
