一些常见分布-正态分布、对数正态分布、伽马分布、卡方分布、t分布、F分布等
目录
正态分布
对数正态分布
伽马分布
伽马函数
贝塔函数
伽马分布
卡方分布
F分布
t分布
附录
参考文献
本文主要介绍一些常见的分布,包括正态分布、对数正态分布、伽马分布、卡方分布、F分布、t分布。给出了分布的定义,推导了概率密度函数,以及函数图像。
正态分布

当,称为标准正态分布,即
。
对数正态分布
对数正态分布(logarithmic normal distribution)是指一个随机变量的对数服从正态分布,则该随机变量服从对数正态分布。对数正态分布从短期来看,与正态分布非常接近。但长期来看,对数正态分布向上分布的数值更多一些。

证明:
假设服从的正态分布为
,概率密度函数为
,
服从的分布为
,概率密度函数为
。显然有
。
下面证明的概率密度函数
表达式如上面所示。
一般我们通过分布函数和概率的定义来证明。
,因为
,则
,
即
,两边对
求导,得到:
,即:
,注意到正态分布概率密度函数
如下:

代入后,可得到表达式如上面所示。
伽马分布
伽马函数
在介绍伽马分布之前,我们先对伽马函数有一个基本理解,伽马函数如下:
![]()
是自变量。伽马函数图像如下:
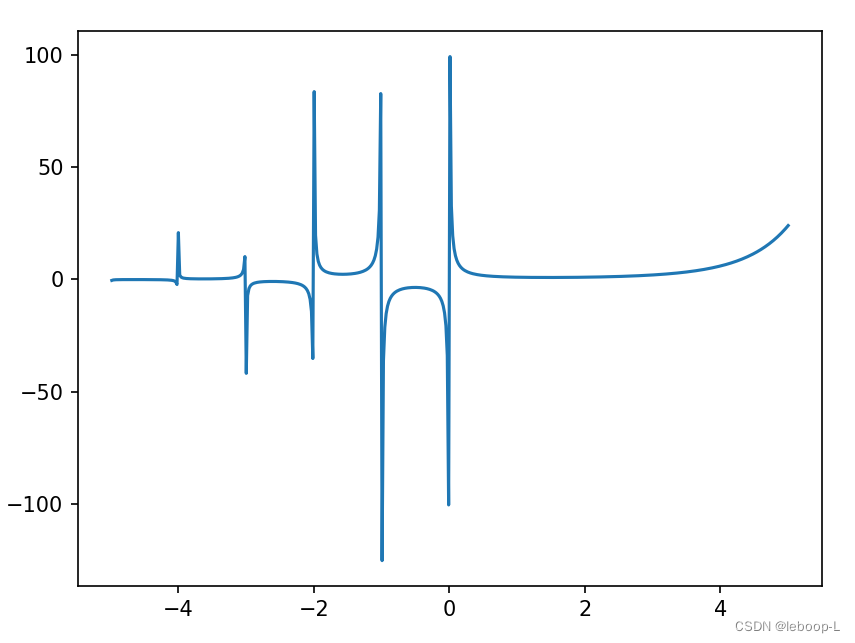
伽马函数图像绘制代码,如下:
import numpy as np
import matplotlib.pyplot as plt
from scipy.special import gammaif __name__ == '__main__':x = np.linspace(-5, 5, 500) # -5到5之间生成500个点y = gamma(x) # 计算y的值,也就是伽马函数的值plt.plot(x, y)plt.show() 为了后面方便推导卡方分布,这里我们证明 。
下面利用标准正态分布的概率密度函数曲线下的面积为1来证明。即:
由正态分布对称性,得到
令进行换元,
因为伽马函数如下:
![]()
知道
伽马函数还有其他很多的函数表达式,这里不再累述。
贝塔函数
在概率统计和其他应用学科中会经常用到伽玛函数和贝塔函数,有的反常积分的计算最后也会归结为贝塔函数或伽玛函数。贝塔函数又称为第一类欧拉积分,而第二类欧拉积分就是大名鼎鼎的伽玛函数Γ(x。贝塔函数具有很好的性质,以及实用的递推公式,另外需要注意的是伽玛函数和贝塔函数之间的关系。贝塔函数如下:
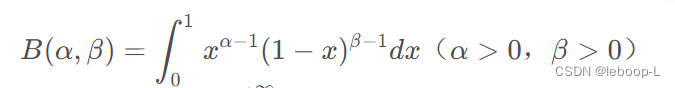
贝塔函数是一个积分形式,为参数。
下面推导伽马函数与贝塔函数之间存在的关系。我们先给出他们的关系:
由伽马函数:
![]()
得到
使用如下积分换元,即
容易得到,并且s=0时,v=1,
时,v=0。变换前后微元关系如下:
则换元后,原式如下:
即:
为了直观地理解贝塔函数,下面我们绘制出贝塔函数的三维曲面图像。代码如下:
import numpy as np
from scipy.special import beta
import matplotlib.pyplot as pltif __name__ == '__main__':# 创建一个网格x, y = np.meshgrid(np.linspace(0.1, 1, 100), np.linspace(0.1, 1, 100))print('x=', '\n', x)print('y=', '\n', y)z = beta(x, y)print('z=', '\n', z)plt.rcParams['font.sans-serif'] = ['Simhei'] # 显示中文fig = plt.figure(figsize=(10, 8))ax = fig.add_subplot(111, projection='3d')ax.tick_params(axis="both", labelsize=12)ax.plot_surface(x, y, z, cmap='viridis')ax.set_xlabel('x', fontsize=13)ax.set_ylabel('y', fontsize=13)ax.set_zlabel('z')ax.set_title('贝塔函数图像')plt.show()
运行结果,如下:
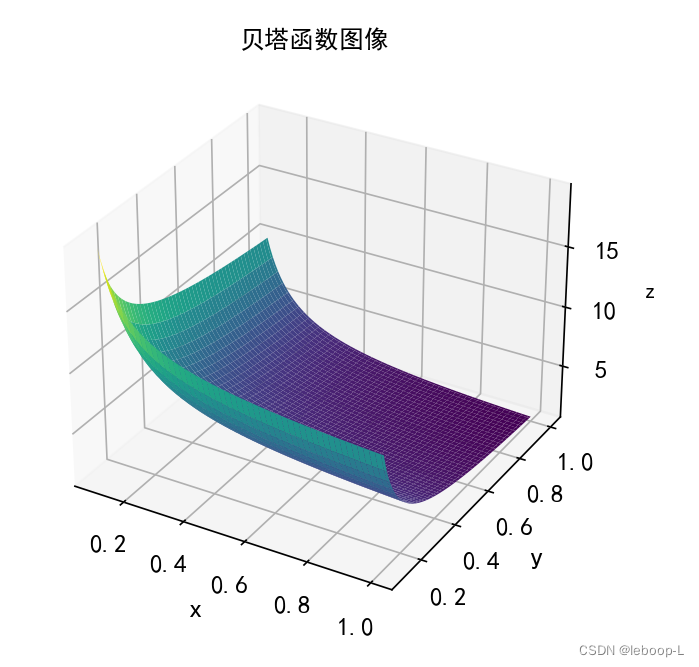
伽马分布
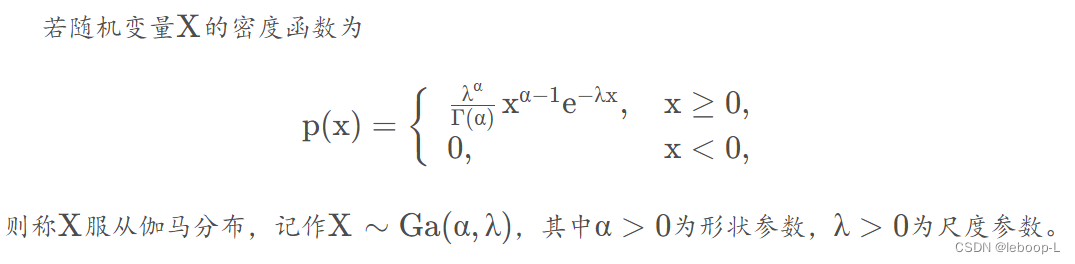
从定义可以看到,伽马分布的概率密度函数的分母中就是伽马函数。 可以通过scipy提供的统计库stats,绘制出正态分布、对数正态分布、伽马分布的概率密度函数曲线,代码如下:
import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import gamma as gamma_dis
from scipy.stats import lognorm
from scipy.stats import normif __name__ == '__main__':alpha = 2 # 伽马分布的形状参数theta = 2 # 伽马分布的比例参数# 创建一个 sample spacex = np.linspace(0, 10, 200)# 计算概率密度函数 (PDF)gamma_pdf = gamma_dis.pdf(x, alpha, scale=theta) # 伽马分布概率密度函数log_norm_pdf = lognorm.pdf(x, loc=0, s=1) # 对数正态分布概率密度函数norm_pdf = norm.pdf(x, loc=0, scale=1) # 正态分布概率密度函数plt.rcParams['font.sans-serif'] = ['Simhei'] # 显示中文# 绘制伽马分布曲线plt.plot(x, gamma_pdf)plt.plot(x, log_norm_pdf)plt.plot(x, norm_pdf)plt.legend(['伽马分布', '对数正态分布', '正态分布']) # 设置图例plt.title('概率密度函数曲线')plt.xlabel('x')plt.ylabel('概率密度函数值')plt.show()
运行结果如下:
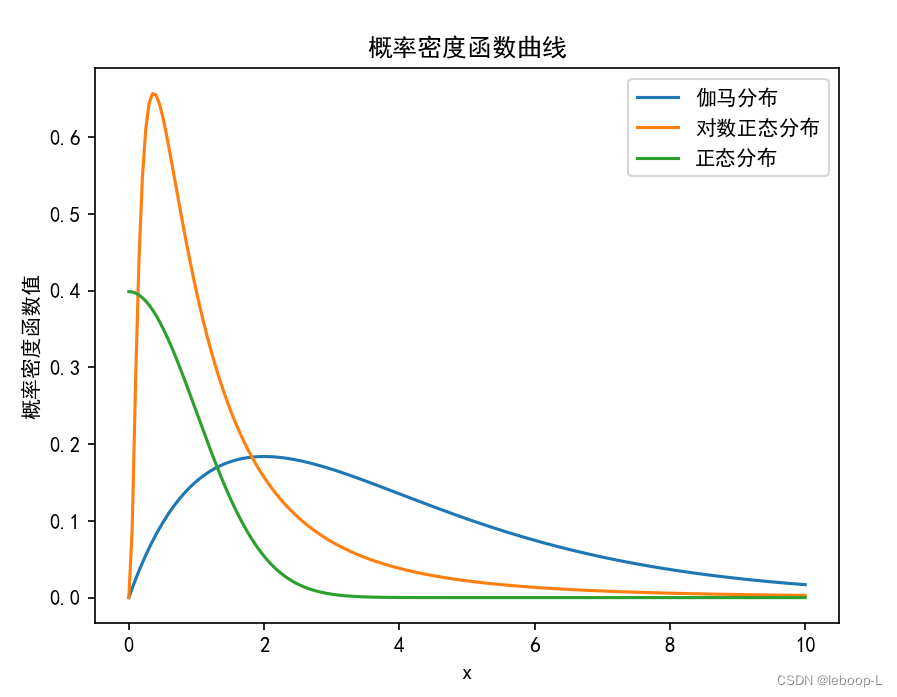
伽马分布有如下重要的性质:
(1)设随机变量,
,且
相互独立,则
。
证明:
假设随机变量的分布为
,概率密度函数为
,随机变量
的概率密度函数分别为
,
。两者的联合概率密度函数为
,因为
相互独立,显然有:
因为
取值都在
,所以
的取值也在
,从而当
时,
。
当时,
,这里将z看成常数,有
使用换元,将x看陈常数,有
,则
,且
,
得到
两边对z求导,得到
。
这就是卷积公式。因为
,
,代入得到
使用换元,当
时,
,并且
,则
根据,得到
,所以
卡方分布
假设n个相互独立的随机变量,均服从标准正态分布(也称独立同分布于标准正态分布)
。则这n个服从标准正态分布的随机变量的平方和
构成一个新的随机变量,其分布规律称为卡方分布(chi-square distribution),记作
,n称为卡方分布的自由度(degree of freedom),记作
。
这个分布由麦克斯韦(James Clerk Maxwell, 1831-1879)在研究空气分子的运动速度的分布时发现的,他发现分子运动速度的平方服从自由度为3的卡方分布,即
。后来又有多人提出这种分布,例如弗里德里希·罗伯特·海尔默特(Friedrich Robert Helmert, 1843-1917)于1875年,故卡方分布有时(在德国常见,因海尔默特是德国人)也称海尔默特分布;另外,这一结果被英国生物统计学家、优生学家、数理统计学创始人和社会达尔文主义理论家卡尔·皮尔逊(Karl Pearson, 1857-1936)推广并于1900年发表。
卡方分布的概率密度函数
下面来推导。
(1)当df=1时,。卡方分布的概率密度函数变为:
假设随机变量的分布函数为
,概率密度函数为
,随机变量
的分布函数为
,概率密度函数为
,随机变量
的分布函数为
,概率密度函数为
。因为
,
服从标准正态分布,有
。
因为
两边对x求导,
因为,所以:
即
事实上,它是的伽马分布,即
。根据如下伽马分布的概率密度函数,很容易得出。
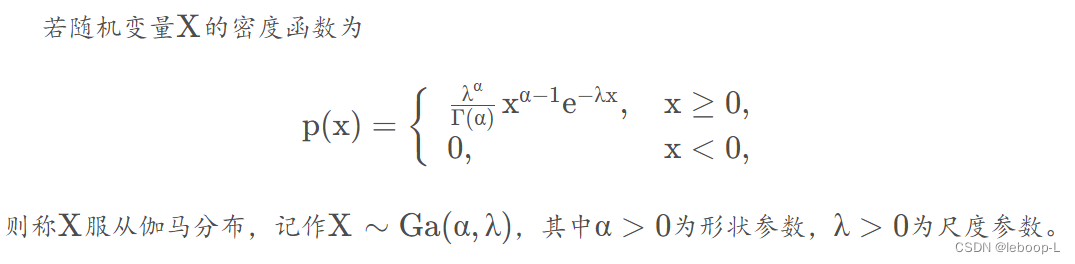
(2)当df=n时,,由上面的结论知道,
。另外因为
相互独立,所以
也相互独立。根据之前证明的如下结论:
如果随机变量,
,且
相互独立,则
。
得到服从
,代入伽马分布,得到如下卡方分布
从结论来看,卡方分布是伽马分布的一个特例,即。也就是说
。
为了直观的观测卡方分布,下面使用python代码绘制卡方分布曲线。代码如下:
import numpy as np
from scipy.special import beta
import matplotlib.pyplot as plt
from scipy import statsif __name__ == '__main__':# # 创建一个网格# x, y = np.meshgrid(np.linspace(0.1, 1, 100), np.linspace(0.1, 1, 100))# print('x=', '\n', x)# print('y=', '\n', y)# z = beta(x, y)# print('z=', '\n', z)#plt.rcParams['font.sans-serif'] = ['Simhei'] # 显示中文# fig = plt.figure(figsize=(10, 8))# ax = fig.add_subplot(111, projection='3d')# ax.tick_params(axis="both", labelsize=12)# ax.plot_surface(x, y, z, cmap='viridis')# ax.set_xlabel('x', fontsize=13)# ax.set_ylabel('y', fontsize=13)# ax.set_zlabel('z')# ax.set_title('贝塔函数图像')# plt.show()X = np.linspace(0.1, 14, 500)plt.subplots(figsize=(8, 5))plt.plot(X, stats.chi2.pdf(X, df=1), label="1 d.o.f")plt.plot(X, stats.chi2.pdf(X, df=2), label="2 d.o.f")plt.plot(X, stats.chi2.pdf(X, df=4), label="4 d.o.f")plt.plot(X, stats.chi2.pdf(X, df=6), label="6 d.o.f")plt.plot(X, stats.chi2.pdf(X, df=11), label="11 d.o.f")plt.title("卡方分布")plt.legend()plt.show()
代码中绘制了自由度为1,2,3,4,11的5个卡方分布,运行结果如下:
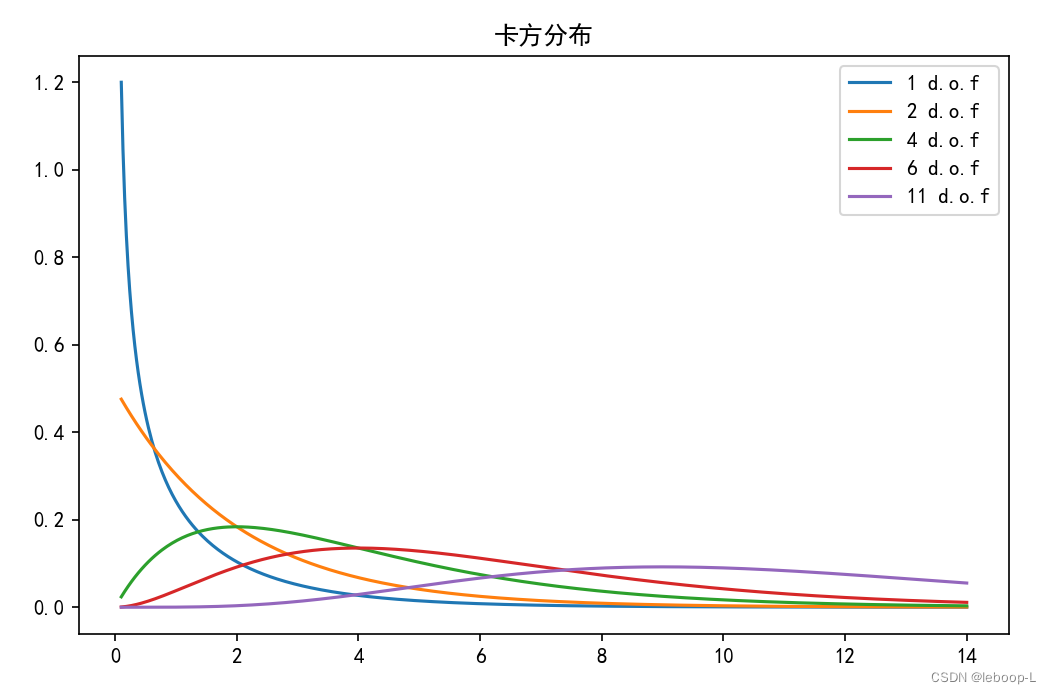
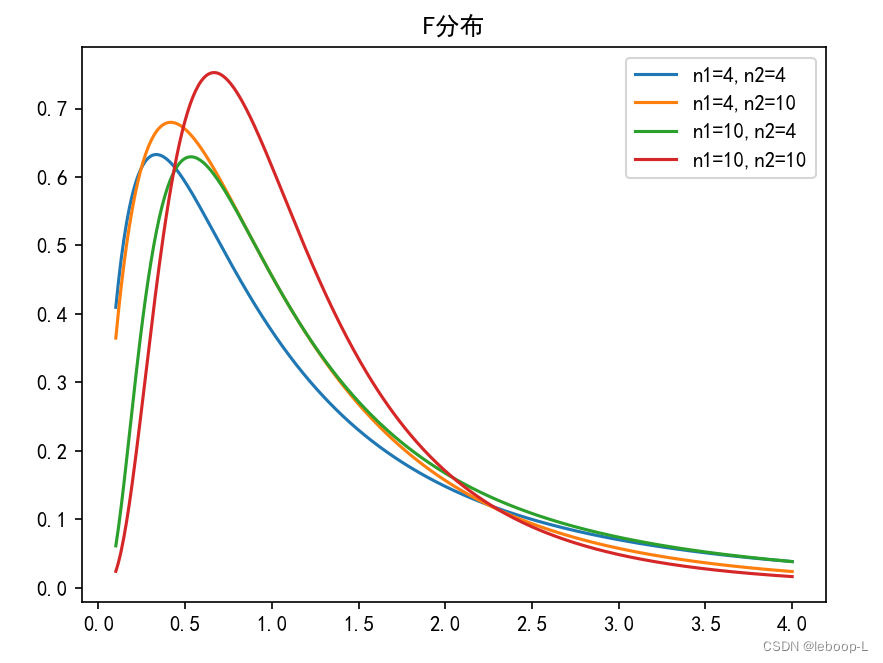
F分布
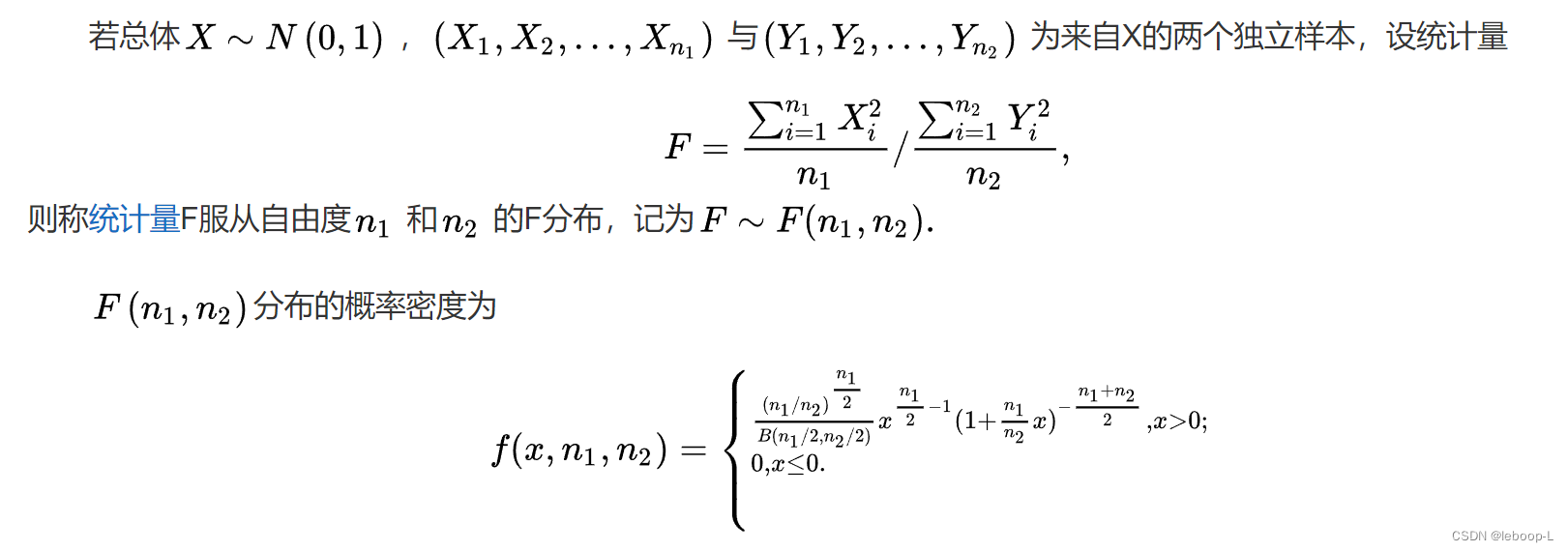
由卡方分布的定义知道,F分布定义可以转换为:如果 ,
,则
为F分布。概率密度函数的证明参见参考文献。
代码如下:
X = np.linspace(0.1, 4, 500)plt.plot(X, stats.f.pdf(X, 4,4), label="n1=4,n2=4")plt.plot(X, stats.f.pdf(X, 4,10), label="n1=4,n2=10")plt.plot(X, stats.f.pdf(X, 10,4), label="n1=10,n2=4")plt.plot(X, stats.f.pdf(X, 10,10), label="n1=10,n2=10")plt.title("F分布")plt.legend()plt.show()运行结果如下:
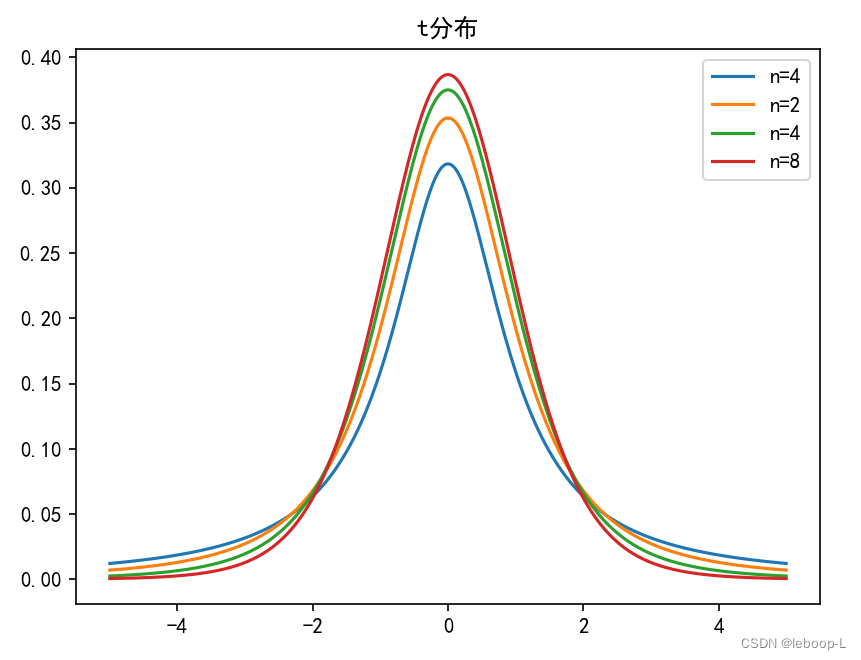
t分布
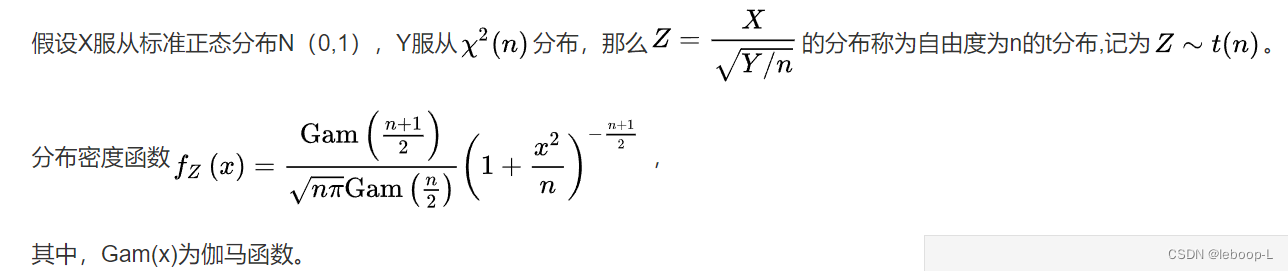
代码如下:
plt.rcParams["axes.unicode_minus"] = False # 设置显示中文后,负号显示受影响,显示负号X = np.linspace(-5, 5, 1500)plt.plot(X, stats.t.pdf(X, 1), label="n=4")plt.plot(X, stats.t.pdf(X, 2), label="n=2")plt.plot(X, stats.t.pdf(X, 4), label="n=4")plt.plot(X, stats.t.pdf(X, 8), label="n=8")plt.title("t分布")plt.legend()plt.show()运行结果如下:
附录
本节所有代码如下:
import numpy as np
from scipy.special import beta
import matplotlib.pyplot as plt
from scipy import statsif __name__ == '__main__':# 创建一个网格x, y = np.meshgrid(np.linspace(0.1, 1, 100), np.linspace(0.1, 1, 100))print('x=', '\n', x)print('y=', '\n', y)z = beta(x, y)print('z=', '\n', z)plt.rcParams['font.sans-serif'] = ['Simhei'] # 显示中文fig = plt.figure(figsize=(10, 8))ax = fig.add_subplot(111, projection='3d')ax.tick_params(axis="both", labelsize=12)ax.plot_surface(x, y, z, cmap='viridis')ax.set_xlabel('x', fontsize=13)ax.set_ylabel('y', fontsize=13)ax.set_zlabel('z')ax.set_title('贝塔函数图像')plt.show()X = np.linspace(0.1, 14, 500)plt.subplots(figsize=(8, 5))plt.plot(X, stats.chi2.pdf(X, df=1), label="1 d.o.f")plt.plot(X, stats.chi2.pdf(X, df=2), label="2 d.o.f")plt.plot(X, stats.chi2.pdf(X, df=4), label="4 d.o.f")plt.plot(X, stats.chi2.pdf(X, df=6), label="6 d.o.f")plt.plot(X, stats.chi2.pdf(X, df=11), label="11 d.o.f")plt.title("卡方分布")plt.legend()plt.show()X = np.linspace(0.1, 4, 500)plt.plot(X, stats.f.pdf(X, 4,4), label="n1=4,n2=4")plt.plot(X, stats.f.pdf(X, 4,10), label="n1=4,n2=10")plt.plot(X, stats.f.pdf(X, 10,4), label="n1=10,n2=4")plt.plot(X, stats.f.pdf(X, 10,10), label="n1=10,n2=10")plt.title("F分布")plt.legend()plt.show()plt.rcParams["axes.unicode_minus"] = False # 设置显示中文后,负号显示受影响,显示负号X = np.linspace(-5, 5, 1500)plt.plot(X, stats.t.pdf(X, 1), label="n=4")plt.plot(X, stats.t.pdf(X, 2), label="n=2")plt.plot(X, stats.t.pdf(X, 4), label="n=4")plt.plot(X, stats.t.pdf(X, 8), label="n=8")plt.title("t分布")plt.legend()plt.show()
参考文献
高数篇(一)-- Gamma 函数 VS Beta 函数
极坐标与直角坐标二重积分转换
F分布概率密度函数的推导
python绘制正态分布及三大抽样分布的概率密度图像
相关文章:

一些常见分布-正态分布、对数正态分布、伽马分布、卡方分布、t分布、F分布等
目录 正态分布 对数正态分布 伽马分布 伽马函数 贝塔函数 伽马分布 卡方分布 F分布 t分布 附录 参考文献 本文主要介绍一些常见的分布,包括正态分布、对数正态分布、伽马分布、卡方分布、F分布、t分布。给出了分布的定义,推导了概率密度函数&…...

科技云报道:押注向量数据库,为时过早?
科技云报道原创。 在大模型的高调火热之下,向量数据库也获得了前所未有的关注。 近两个月内,向量数据库迎来融资潮,Qdrant、Chroma、Weaviate先后获得融资,Pinecone宣布1亿美元B轮融资,估值达到7.5亿美元。 东北证券…...

铭控传感亮相2023国际物联网展,聚焦“多场景物联感知方案”应用
金秋九月,聚焦IoT基石技术,荟萃最全物联感知企业,齐聚IOTE 2023第20届国际物联网展深圳站。铭控传感携智慧楼宇,数字工厂,智慧消防,智慧泵房等多场景物联感知方案及多品类无线传感器闪亮登场,现…...

前端demo: 实现对图片进行上传前的压缩功能
前端可以使用canvas和File API来对图片进行压缩和缩放处理,以下是一个示例代码 : 压缩方法compressImg这段代码是实现对图片进行上传前的压缩功能 1. 定义了一个压缩图片的函数 compressImg,接受两个参数:file表示要压缩的文件,q…...
)
计算机网络(文章链接汇总)
参考引用 计算机网络微课堂-湖科大教书匠计算机网络(第7版)-谢希仁 计算机网络(一):概述计算机网络(二):物理层计算机网络(三):数据链路层计算机网…...

黑科技-Android
1热更新(热修复):apk不用发版,就能修复bug 原理:我们修复好了bug的时候,把那些有改动的java源码编译成class,再打包成dex,然后通过反射技术放到dexElements数组的最前面,…...
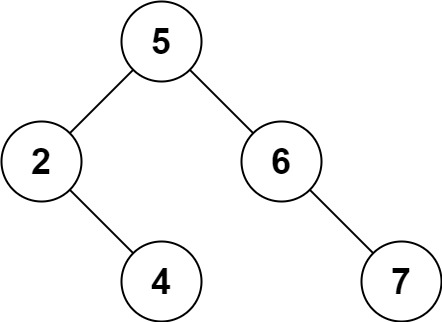
450. 删除二叉搜索树中的节点
给定一个二叉搜索树的根节点 root 和一个值 key,删除二叉搜索树中的 key 对应的节点,并保证二叉搜索树的性质不变。返回二叉搜索树(有可能被更新)的根节点的引用。 一般来说,删除节点可分为两个步骤: 首先…...

python安全工具开发基础
文章目录 拷贝、with、is深拷贝、浅拷贝with 三器一闭迭代器生成器闭包装饰器 动态绑定垃圾回收网络编程UdpTcp 协程mysql预处理防止注入 redis未授权/弱密码 拷贝、with 、is a [11, 22, 33] b [11, 22, 33] ca print(id(a)) print(id(b)) print(id(c))print(a b) print(…...

26 docker前后端部署
[参考博客]((257条消息) DockerNginx部署前后端分离项目(SpringBootVue)的详细教程_在docker中安装nginx实现前后端分离_这里是杨杨吖的博客-CSDN博客) (DockerNginx部署前后端分离项目(SpringBootVue)) 安装docker # 1、yum 包更新到最新 yum update # 2、安装需要的软件包…...
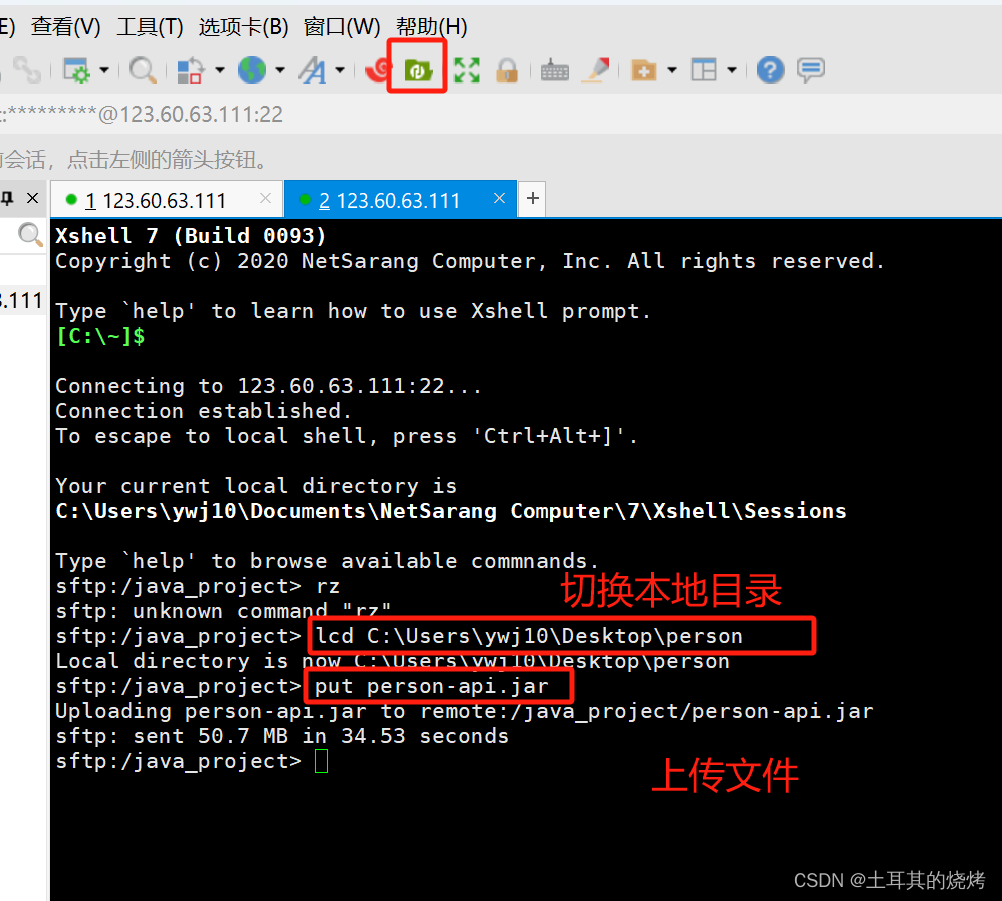
[linux] SFTP文件传输基本命令 --- xshell 直接上传文件
2.sftp - 上传文件:如果上传/下载的是文件夹, 在put/get命令后加上-r参数即可。 上传文件: 把本地服务器的/www/wwwroot目录下面的study.log文件上传到远程服务器的/www/server目录下。 sftp> lcd /www/wwwroot sftp> put study.log /www/server…...

Tomcat 多实例
一、Tomcat 多实例 1、概念: Tomcat 多实例是指在同一台服务器上运行多个独立的 Tomcat 服务器实例。它们可以同时运行在同一台物理服务器或虚拟服务器上,但它们彼此之间是相互独立的,有各自的配置、应用程序和资源。 2、配置:…...

全民拼购模式:电商的新趋势和机遇
全民拼购模式是一种基于社交电商的新型模式,它通过拼团、拼购等方式,让消费者享受更优惠的价格和更便捷的购物体验。这种模式的出现,不仅为电商平台注入了新的活力,也成为了消费者追求高性价比商品的新选择。 全民拼购模式有以下…...

免费使用,媲美Midjourney!微软在Bing Chat等提供—DALL-E 3
微软在官网宣布,将OpenAI最新模型DALL-E 3集成在Bing Chat和Bing Image Create中,并免费提供给用户使用。 据悉,DALL-E 3是一款类Midjourney产品,通过文本就能生成二次元、3D、朋克、涂鸦、素描、黑白、极简、印象派、位面像素等…...

Nacos中AP和CP 切换
CAP理论 这个定理的内容是指的是在一个分布式系统中、Consistency(一致性)、 Availability(可用性)、Partition tolerance(分区容错性),三者不可得兼。 一致性(C):在分布式系统中&a…...
服务器中勒索病毒怎么解决?勒索病毒解密,数据恢复
服务器中勒索病毒是一件低频、高概率的事情。而且一旦用户的服务器中招以后,想要处理无论是经济成本还是时间成本都非常的高。也会对企业的生产经营造成很大的影响。所以绝大多数企业主都很关心服务器中勒索病毒后怎么解决。针对这个问题,云天数据恢复中…...
)
全面解析UDP协议(特点、报文格式、UDP和TCP的区别)
了解UDP(User Datagram Protocol) UDP是无连接通信协议,即在数据传输时,数据的发送端和接收端不建立逻辑连接。简单来说,当一台计算机向另外一台计算机发送数据时,发送端不会确认接收端是否存在࿰…...
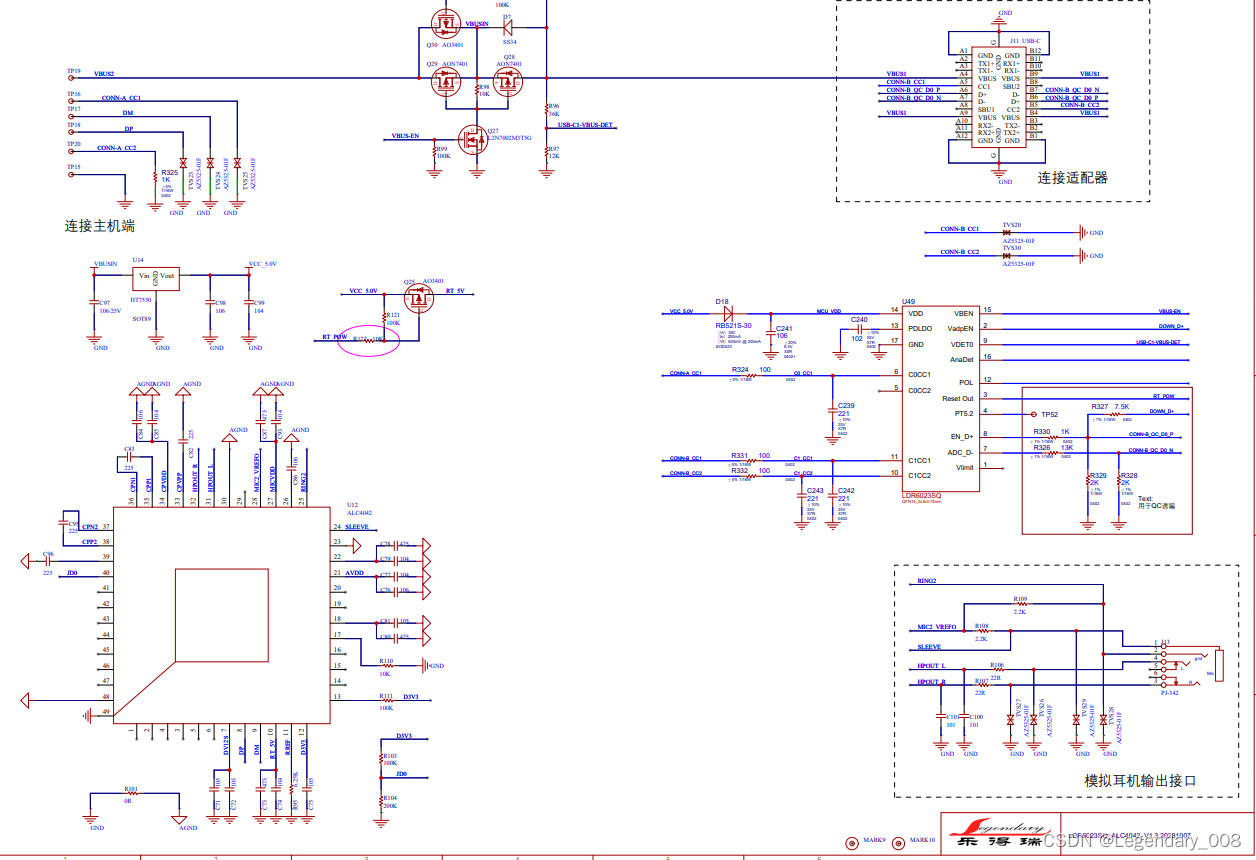
iPhone15手机拓展坞方案,支持手机快充+传输数据功能
手机拓展坞的组合有何意义?首先是数据存储场景,借助拓展坞扩展出的接口,可以连接U盘、移动硬盘等采用USB接口的设备,实现大文件的快速存储或者流转;其次是图片、视频的读取场景,想要读取相机、无人机SD/TF存…...
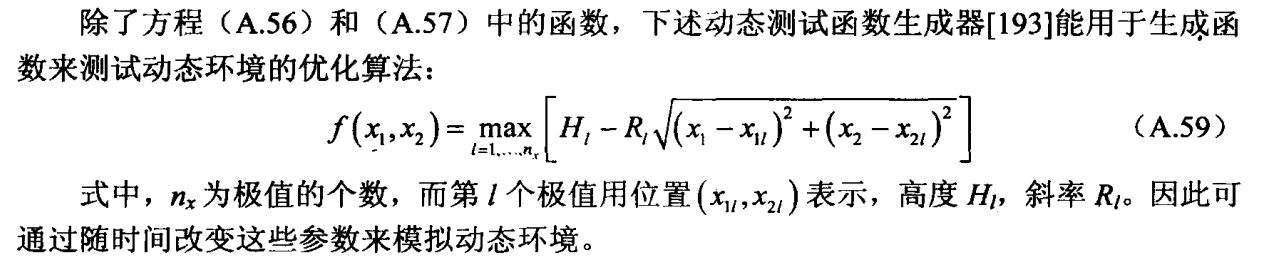
优化理论笔记
目录 一、前言 二、优化问题的基本要素 三、优化问题分类 四、最优值类型 五、最优化方法分类 六、非约束优化 1、问题定义 2、优化算法 1)一般局部搜索过程 2)集束搜索 3)禁忌搜索 4)模拟退火 5)蛙跳算法…...

FastAPI学习-23.异常处理器 exception_handler
前言 通常我们可以通过 raise 抛出一个 HTTPException 异常,请求参数不合法会抛出RequestValidationError 异常,这是最常见的2种异常。 HTTPException 异常 向客户端返回 HTTP 错误响应,可以使用 raise 触发 HTTPException。 from fastap…...
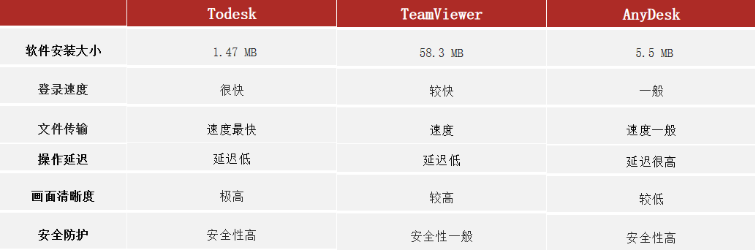
国庆出游远程实测:ToDesk 、TeamViewer、AnyDesk远程控制软件稳定性
ToDesk 、TeamViewer、AnyDesk远程控制软件稳定性 【前言】【实测软件】【测试环境】【实操体验】1. 软件安装2. 登录速度3. 文件传输4. 操作延迟5. 画面清晰度6. 安全防护 【本文小结】 【前言】 随着科技的不断发展,远程控制软件已成为我们生活中不可或缺的一部分…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

Unsafe Fileupload篇补充-木马的详细教程与木马分享(中国蚁剑方式)
在之前的皮卡丘靶场第九期Unsafe Fileupload篇中我们学习了木马的原理并且学了一个简单的木马文件 本期内容是为了更好的为大家解释木马(服务器方面的)的原理,连接,以及各种木马及连接工具的分享 文件木马:https://w…...

使用LangGraph和LangSmith构建多智能体人工智能系统
现在,通过组合几个较小的子智能体来创建一个强大的人工智能智能体正成为一种趋势。但这也带来了一些挑战,比如减少幻觉、管理对话流程、在测试期间留意智能体的工作方式、允许人工介入以及评估其性能。你需要进行大量的反复试验。 在这篇博客〔原作者&a…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...
