【C++】set map 的底层封装
在了解底层封装之前除了对set和map的使用情况要有一定了解,还需要先学习一下二叉搜索树,AVL树,红黑树这些数据结构。
【C++】二叉搜索树
【C++】AVL树 & 红黑树
RBTree.h
enum Colour
{RED,BLACK
};template<class T>
class RBTreeNode
{
public:RBTreeNode(const T& data): _data(data), _left(nullptr), _right(nullptr), _parent(nullptr){}T _data;RBTreeNode<T>* _left;RBTreeNode<T>* _right;RBTreeNode<T>* _parent;Colour _col;
};template<class T, class Ref, class Ptr>
// 红黑树的迭代器实现
class __RBTreeIterator
{
public:typedef RBTreeNode<T> Node;typedef __RBTreeIterator<T, Ref, Ptr> Self;
public:__RBTreeIterator(Node* node): _node(node){}Ref operator*(){return _node->_data;}Ptr operator->(){return &_node->_data;}bool operator!=(const Self& s) const{return _node != s._node;}bool operator==(const Self& s) const{return _node == s._node;}Self& operator++(){// 右子树不为空if (_node->_right){// ++就是找右子树的最左节点Node* left = _node->_right;while (left->_left){left = left->_left;}_node = left;}// 右子树为空else{// ++就是找不是其右孩子的祖先Node* parent = _node->_parent;Node* cur = _node;while (parent && parent->_right == cur){cur = cur->_parent;parent = parent->_parent;}_node = parent;}return *this;}Self& operator--(){// 左子树不为空if (_node->_left){// --就是找左子树的最右节点Node* right = _node->_left;while (right->_right){right = right->_right;}_node = right;}// 左子树为空else{// --就是找不是其左孩子的祖先Node* parent = _node->_parent;Node* cur = _node;while (parent && parent->_left == cur){cur = cur->_parent;parent = parent->_parent;}_node = parent;}return *this;}
public:Node* _node;
};// KeyOfT: 用于获取T中的key的一个仿函数类
template<class K, class T, class KeyOfT>
class RBTree
{
private:typedef RBTreeNode<T> Node;
public:typedef __RBTreeIterator<T, T&, T*> iterator;RBTree(Node* root = nullptr): _root(root){}// begin() 就是找红黑树的最左节点iterator begin(){Node* left = _root;while (left && left->_left){left = left->_left;}return iterator(left);}// 因为迭代器是左闭右开,所以end()的迭代器设置为空iterator end(){return iterator(nullptr);}pair<iterator, bool> Insert(const T& data){KeyOfT kot;if (_root == nullptr){_root = new Node(data);_root->_col = BLACK;return make_pair(iterator(_root), true);}Node* parent = nullptr;Node* cur = _root;while (cur){if (kot(data) > kot(cur->_data)){parent = cur;cur = cur->_right;}else if (kot(data) < kot(cur->_data)){parent = cur;cur = cur->_left;}else{return make_pair(iterator(cur), false);}}cur = new Node(data);cur->_col = RED;// 保存cur用于返回Node* newnode = cur;if (kot(data) > kot(parent->_data)){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;while (parent && parent->_col == RED){Node* grandparent = parent->_parent;if (parent == grandparent->_left){Node* uncle = grandparent->_right;if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandparent->_col = RED;cur = grandparent;parent = cur->_parent;}else{if (cur == parent->_left){RotateR(grandparent);parent->_col = BLACK;grandparent->_col = RED;}else{RotateL(parent);RotateR(grandparent);cur->_col = BLACK;grandparent->_col = RED;}break;}}else{Node* uncle = grandparent->_left;if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandparent->_col = RED;cur = grandparent;parent = cur->_parent;}else{if (cur == parent->_right){RotateL(grandparent);parent->_col = BLACK;grandparent->_col = RED;}else{RotateR(parent);RotateL(grandparent);cur->_col = BLACK;grandparent->_col = RED;}break;}}}_root->_col = BLACK;return make_pair(iterator(newnode), true);}
private:void RotateL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL){subRL->_parent = parent;}Node* ppNode = parent->_parent;subR->_left = parent;parent->_parent = subR;if (_root == parent){_root = subR;subR->_parent = nullptr;}else{if (ppNode->_left == parent){ppNode->_left = subR;}else{ppNode->_right = subR;}subR->_parent = ppNode;}}void RotateR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR){subLR->_parent = parent;}Node* ppNode = parent->_parent;subL->_right = parent;parent->_parent = subL;if (_root == parent){_root = subL;subL->_parent = nullptr;}else{if (ppNode->_left == parent){ppNode->_left = subL;}else{ppNode->_right = subL;}subL->_parent = ppNode;}}
private:Node* _root;
};
Set.h
#include "RBTree.h"namespace zs
{template<class K>class set{public:class SetKeyOfT{public:const K& operator()(const K& key){return key;}};typedef typename RBTree<K, K, SetKeyOfT>::iterator iterator;iterator begin(){return _t.begin();}iterator end(){return _t.end();}pair<iterator, bool> insert(const K& key){return _t.Insert(key);}private:// set的底层就是一棵红黑树RBTree<K, K, SetKeyOfT> _t;};
}
Map.h
#include "RBTree.h"namespace zs
{template<class K, class V>class map{public:class MapKeyOfT{public:const K& operator()(const pair<K, V>& kv){return kv.first;}};typedef typename RBTree<K, pair<K,V>, MapKeyOfT>::iterator iterator;iterator begin(){return _t.begin();}iterator end(){return _t.end();}pair<iterator, bool> insert(const pair<K, V>& kv){return _t.Insert(kv);}// map支持[]操作V& operator[](const K& key){pair<iterator, bool> ret = insert(make_pair(key, V()));return ret.first->second;}private:// map的底层就是一棵红黑树RBTree<K, pair<K, V>, MapKeyOfT> _t;};}
相关文章:

【C++】set map 的底层封装
在了解底层封装之前除了对set和map的使用情况要有一定了解,还需要先学习一下二叉搜索树,AVL树,红黑树这些数据结构。 【C】二叉搜索树 【C】AVL树 & 红黑树 RBTree.h enum Colour {RED,BLACK };template<class T> class RBTreeNo…...

JavaWeb整体介绍
JavaWeb整体介绍 什么是Java Web Web:全球广域网,也称为万维网(www),能够通过浏览器访问的网站JavaWeb:是使用Java技术解决相关web互联网领域的技术栈(就是用java开发网站) 网页&a…...
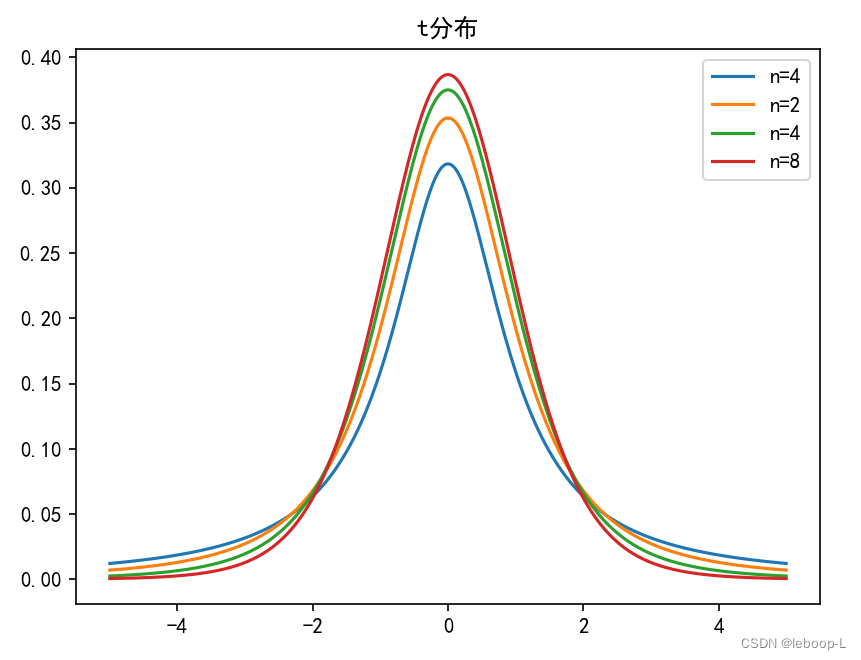
一些常见分布-正态分布、对数正态分布、伽马分布、卡方分布、t分布、F分布等
目录 正态分布 对数正态分布 伽马分布 伽马函数 贝塔函数 伽马分布 卡方分布 F分布 t分布 附录 参考文献 本文主要介绍一些常见的分布,包括正态分布、对数正态分布、伽马分布、卡方分布、F分布、t分布。给出了分布的定义,推导了概率密度函数&…...

科技云报道:押注向量数据库,为时过早?
科技云报道原创。 在大模型的高调火热之下,向量数据库也获得了前所未有的关注。 近两个月内,向量数据库迎来融资潮,Qdrant、Chroma、Weaviate先后获得融资,Pinecone宣布1亿美元B轮融资,估值达到7.5亿美元。 东北证券…...

铭控传感亮相2023国际物联网展,聚焦“多场景物联感知方案”应用
金秋九月,聚焦IoT基石技术,荟萃最全物联感知企业,齐聚IOTE 2023第20届国际物联网展深圳站。铭控传感携智慧楼宇,数字工厂,智慧消防,智慧泵房等多场景物联感知方案及多品类无线传感器闪亮登场,现…...

前端demo: 实现对图片进行上传前的压缩功能
前端可以使用canvas和File API来对图片进行压缩和缩放处理,以下是一个示例代码 : 压缩方法compressImg这段代码是实现对图片进行上传前的压缩功能 1. 定义了一个压缩图片的函数 compressImg,接受两个参数:file表示要压缩的文件,q…...
)
计算机网络(文章链接汇总)
参考引用 计算机网络微课堂-湖科大教书匠计算机网络(第7版)-谢希仁 计算机网络(一):概述计算机网络(二):物理层计算机网络(三):数据链路层计算机网…...

黑科技-Android
1热更新(热修复):apk不用发版,就能修复bug 原理:我们修复好了bug的时候,把那些有改动的java源码编译成class,再打包成dex,然后通过反射技术放到dexElements数组的最前面,…...
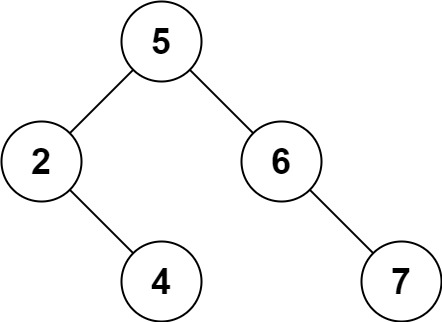
450. 删除二叉搜索树中的节点
给定一个二叉搜索树的根节点 root 和一个值 key,删除二叉搜索树中的 key 对应的节点,并保证二叉搜索树的性质不变。返回二叉搜索树(有可能被更新)的根节点的引用。 一般来说,删除节点可分为两个步骤: 首先…...

python安全工具开发基础
文章目录 拷贝、with、is深拷贝、浅拷贝with 三器一闭迭代器生成器闭包装饰器 动态绑定垃圾回收网络编程UdpTcp 协程mysql预处理防止注入 redis未授权/弱密码 拷贝、with 、is a [11, 22, 33] b [11, 22, 33] ca print(id(a)) print(id(b)) print(id(c))print(a b) print(…...

26 docker前后端部署
[参考博客]((257条消息) DockerNginx部署前后端分离项目(SpringBootVue)的详细教程_在docker中安装nginx实现前后端分离_这里是杨杨吖的博客-CSDN博客) (DockerNginx部署前后端分离项目(SpringBootVue)) 安装docker # 1、yum 包更新到最新 yum update # 2、安装需要的软件包…...
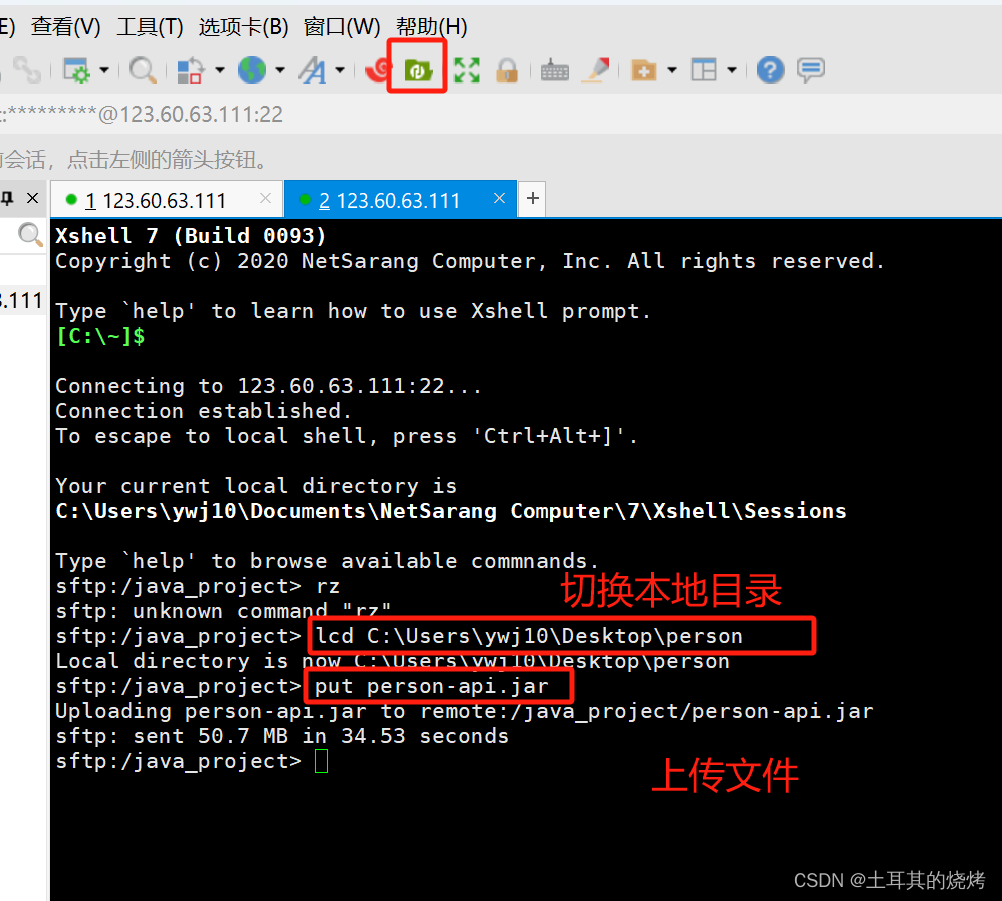
[linux] SFTP文件传输基本命令 --- xshell 直接上传文件
2.sftp - 上传文件:如果上传/下载的是文件夹, 在put/get命令后加上-r参数即可。 上传文件: 把本地服务器的/www/wwwroot目录下面的study.log文件上传到远程服务器的/www/server目录下。 sftp> lcd /www/wwwroot sftp> put study.log /www/server…...

Tomcat 多实例
一、Tomcat 多实例 1、概念: Tomcat 多实例是指在同一台服务器上运行多个独立的 Tomcat 服务器实例。它们可以同时运行在同一台物理服务器或虚拟服务器上,但它们彼此之间是相互独立的,有各自的配置、应用程序和资源。 2、配置:…...

全民拼购模式:电商的新趋势和机遇
全民拼购模式是一种基于社交电商的新型模式,它通过拼团、拼购等方式,让消费者享受更优惠的价格和更便捷的购物体验。这种模式的出现,不仅为电商平台注入了新的活力,也成为了消费者追求高性价比商品的新选择。 全民拼购模式有以下…...

免费使用,媲美Midjourney!微软在Bing Chat等提供—DALL-E 3
微软在官网宣布,将OpenAI最新模型DALL-E 3集成在Bing Chat和Bing Image Create中,并免费提供给用户使用。 据悉,DALL-E 3是一款类Midjourney产品,通过文本就能生成二次元、3D、朋克、涂鸦、素描、黑白、极简、印象派、位面像素等…...

Nacos中AP和CP 切换
CAP理论 这个定理的内容是指的是在一个分布式系统中、Consistency(一致性)、 Availability(可用性)、Partition tolerance(分区容错性),三者不可得兼。 一致性(C):在分布式系统中&a…...
服务器中勒索病毒怎么解决?勒索病毒解密,数据恢复
服务器中勒索病毒是一件低频、高概率的事情。而且一旦用户的服务器中招以后,想要处理无论是经济成本还是时间成本都非常的高。也会对企业的生产经营造成很大的影响。所以绝大多数企业主都很关心服务器中勒索病毒后怎么解决。针对这个问题,云天数据恢复中…...
)
全面解析UDP协议(特点、报文格式、UDP和TCP的区别)
了解UDP(User Datagram Protocol) UDP是无连接通信协议,即在数据传输时,数据的发送端和接收端不建立逻辑连接。简单来说,当一台计算机向另外一台计算机发送数据时,发送端不会确认接收端是否存在࿰…...
iPhone15手机拓展坞方案,支持手机快充+传输数据功能
手机拓展坞的组合有何意义?首先是数据存储场景,借助拓展坞扩展出的接口,可以连接U盘、移动硬盘等采用USB接口的设备,实现大文件的快速存储或者流转;其次是图片、视频的读取场景,想要读取相机、无人机SD/TF存…...
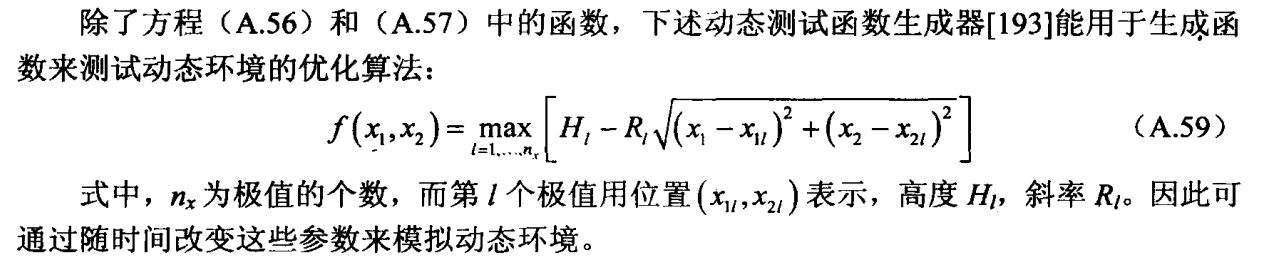
优化理论笔记
目录 一、前言 二、优化问题的基本要素 三、优化问题分类 四、最优值类型 五、最优化方法分类 六、非约束优化 1、问题定义 2、优化算法 1)一般局部搜索过程 2)集束搜索 3)禁忌搜索 4)模拟退火 5)蛙跳算法…...

第19节 Node.js Express 框架
Express 是一个为Node.js设计的web开发框架,它基于nodejs平台。 Express 简介 Express是一个简洁而灵活的node.js Web应用框架, 提供了一系列强大特性帮助你创建各种Web应用,和丰富的HTTP工具。 使用Express可以快速地搭建一个完整功能的网站。 Expre…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...
:爬虫完整流程)
Python爬虫(二):爬虫完整流程
爬虫完整流程详解(7大核心步骤实战技巧) 一、爬虫完整工作流程 以下是爬虫开发的完整流程,我将结合具体技术点和实战经验展开说明: 1. 目标分析与前期准备 网站技术分析: 使用浏览器开发者工具(F12&…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...
