Web开发-单例模式
目录
- 单例模式介绍
- 代码实现单例模式
单例模式介绍
- 单例模式是一种创建型设计模式,它确保一个类只有一个实例,并提供一个全局访问点。
- 单例模式可以通过private属性实现。通过将类的构造函数设为private,可以防止类在外部被实例化。
- 单例模式通常会提供一个静态方法来获取类的唯一实例。
代码实现单例模式
在 Java 中,可以使用以下代码实现单例模式:
public class Singleton { private static Singleton instance;private Singleton() { // 防止通过反射创建多个实例 if (instance != null) { throw new IllegalStateException("Singleton instance already exists"); } }public static Singleton getInstance() { if (instance == null) { instance = new Singleton(); } return instance; }
}
在上面的代码中,Singleton 类有一个私有的构造函数和一个静态的 getInstance() 方法,用于获取 Singleton 类的唯一实例。当第一次调用 getInstance() 方法时,会创建一个 Singleton 实例,并将其存储在 instance 变量中。之后,每次调用 getInstance() 方法时,都会返回已经创建的实例,而不是创建新的实例。
要使用 Singleton 类的实例,可以像下面这样:
Singleton singleton = Singleton.getInstance();
这样,就可以确保在整个应用程序中只有一个 Singleton 实例,可以全局访问该实例。
相关文章:

Web开发-单例模式
目录 单例模式介绍代码实现单例模式 单例模式介绍 单例模式是一种创建型设计模式,它确保一个类只有一个实例,并提供一个全局访问点。单例模式可以通过private属性实现。通过将类的构造函数设为private,可以防止类在外部被实例化。单例模式通…...
MySQL:温备份和恢复-mysqldump (4)
介绍 温备:同样是在数据库运行的时候进行备份的,但对当前数据库的操作会产生影响。(只可以读操作,不可以写操作) 温备份的优点: 1.可在表空间或数据文件级备份,备份时间短。 2.备份时数据库依然…...
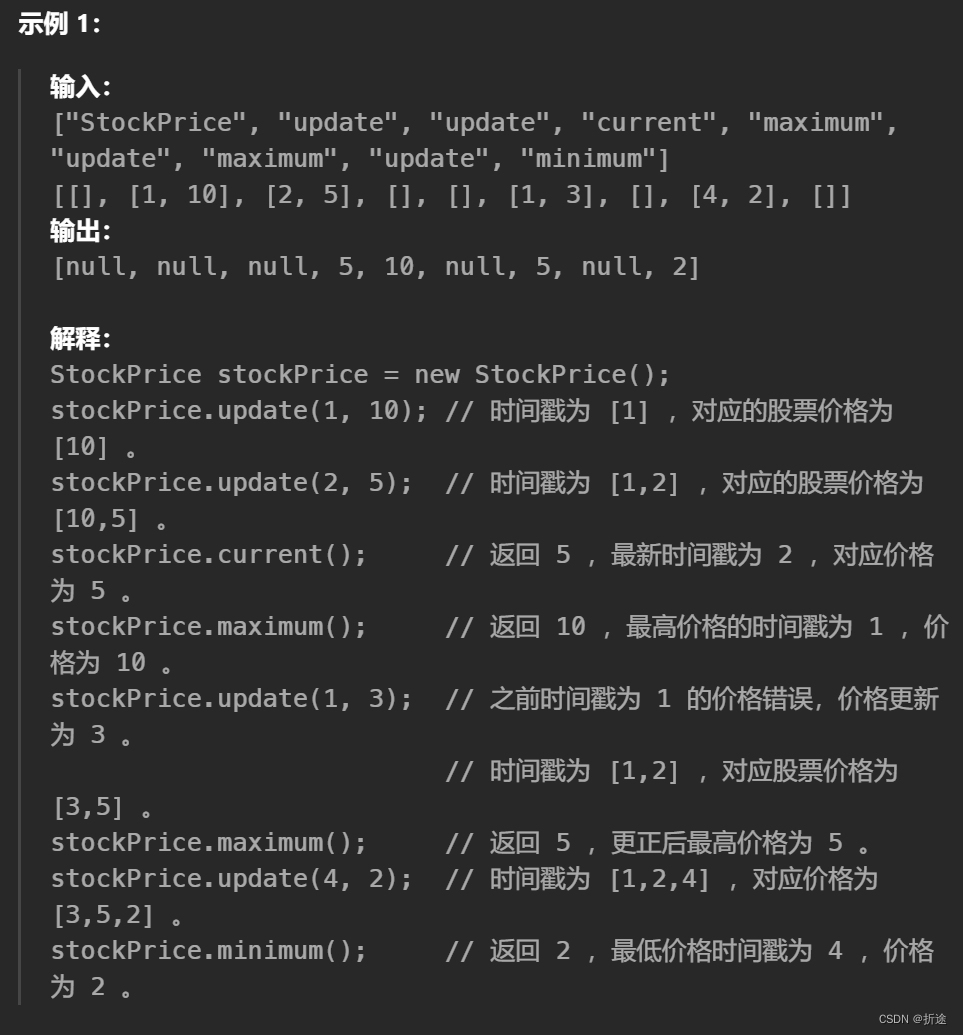
【力扣每日一题】2023.10.8 股票价格波动
目录 题目: 示例: 分析: 代码: 题目: 示例: 分析: 这道题是程序设计题,要我们实现一个类,一共是四个功能,第一个是给一个时间戳和价格,表示该…...

Linux隐藏文件或文件夹
在Linux中,以点(.)开头的文件或文件夹是隐藏文件或隐藏文件夹。要创建一个隐藏文件或文件夹,可以使用以下命令: 创建隐藏文件: touch .filename这将在当前目录下创建一个名为 “.filename” 的隐藏文件。…...
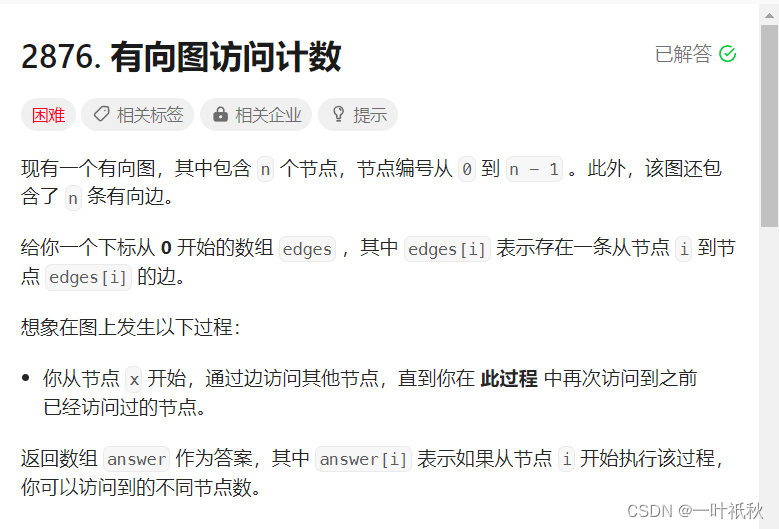
leetcode - 365周赛
一,2873.有序三元组中的最大值 I 该题的数据范围小,直接遍历: class Solution {public long maximumTripletValue(int[] nums) {int n nums.length;long ans 0;for(int i0; i<n-2; i){for(int ji1; j<n-1; j){for(int kj1; k<…...

为什么mac上有的软件删除不掉?
对于Mac用户来说,软件卸载通常是一个相对简单的过程。然而,有时你可能会发现某些软件似乎“顽固不化”,即使按照常规方式尝试卸载,也依然存在于你的电脑上。这到底是为什么呢?本文将探讨这一问题的可能原因。 1.卸载失…...
【vue3】wacth监听,监听ref定义的数据,监听reactive定义的数据,详解踩坑点
假期第二篇,对于基础的知识点,我感觉自己还是很薄弱的。 趁着假期,再去复习一遍 之前已经记录了一篇【vue3基础知识点-computed和watch】 今天在学习的过程中发现,之前记录的这一篇果然是很基础的,很多东西都讲的不够…...
跨境电商如何通过软文建立品牌形象?
在全球产业链结构重塑后的今天,越来越多的企业意识到想要可持续发展,就需要在建立品牌形象,在用户心中留下深刻印象,那么应该如何有效建立品牌形象呢?可以利用软文来打造品牌形象,接下来媒介盒子就告诉大家…...
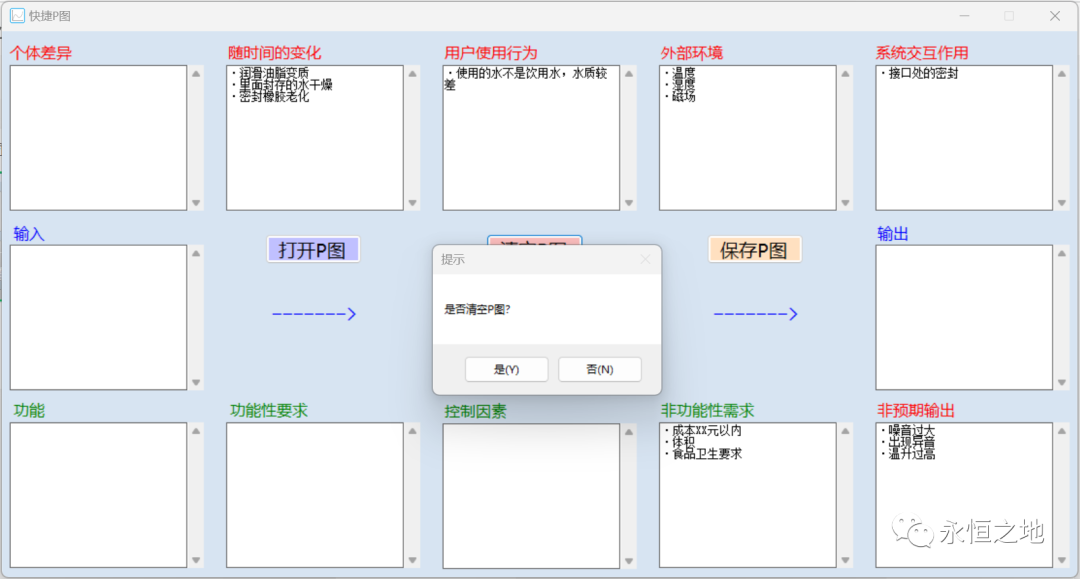
我做了一个简易P图(参数图)分析软件
P图(即参数图,Parameter Diagram),是一个结构化的工具,帮助大家对产品更好地进行分析。 典型P图格式 P图最好是和FMEA软件联动起来,如国可工软的FMEA软件有P图分析这个功能。 单纯的P图分析软件很少,为了方便做P图分…...
:状态,按键分区,算子状态,状态后端。容错机制,检查点,保存点。状态一致性。flink与kafka整合)
209.Flink(四):状态,按键分区,算子状态,状态后端。容错机制,检查点,保存点。状态一致性。flink与kafka整合
一、状态 1.概述 算子任务可以分为有状态、无状态两种。 无状态:filter,map这种,每次都是独立事件有状态:sum这种,每次处理数据需要额外一个状态值来辅助。这个额外的值就叫“状态”2.状态的分类 (1)托管状态(Managed State)和原始状态(Raw State) 托管状态就是由…...
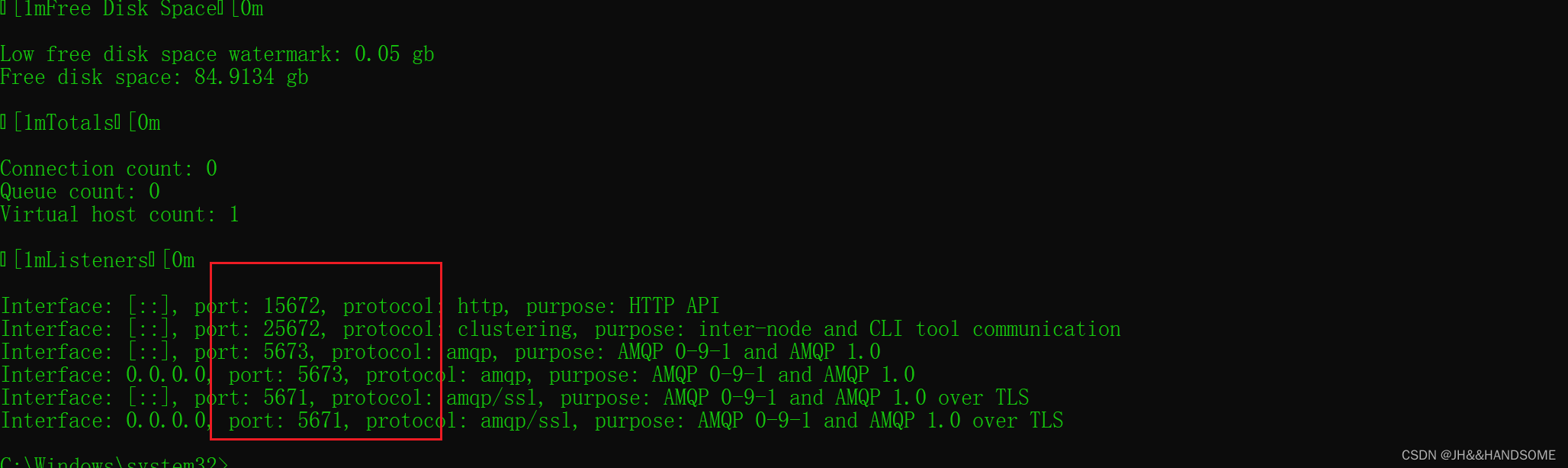
rabbitmq查看节点信息命令失败
不影响访问rabbitmq,但是无法使用 命令查看节点信息 等 查看节点信息命令:rabbitmq-diagnostics status --node rabbitJHComputer Error: unable to perform an operation on node ‘rabbitJHComputer‘. Please see diagnostics informatio rabbitmq-…...
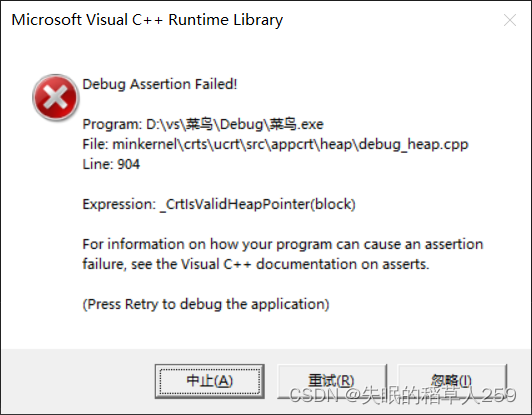
c语言动态内存分布
前言: 随着我们深入的学习c语言,之前使用的静态内存分配已经难以满足我们的实际需求。比如前面我们的通讯录功能的实现,如果只是静态内存分配,那么也就意味着程序开始的内存分配大小就是固定的,应该开多大的空间呢&am…...

1.3.2有理数减法(第一课时)作业设计
【学习目标】 1.理解有理数减法法则,能熟练地进行有理数的减法运算. 2.感受有理数减法与加法对立统一的辨证思想,体会转化的思想方法....
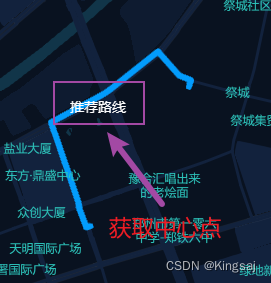
vue3 -- ts封装 Turf.js地图常用方法
Turf.js中文网 地理空间分析库,处理各种地图算法 文档地址 安装 Turf 库 npm install @turf/turf创建src/hooks/useTurf.ts 文件1:获取线中心点 效果: 代码: useTurf.ts import * as turf from @turf/turf// 获取线中心点 export class CenterPointOfLine {...
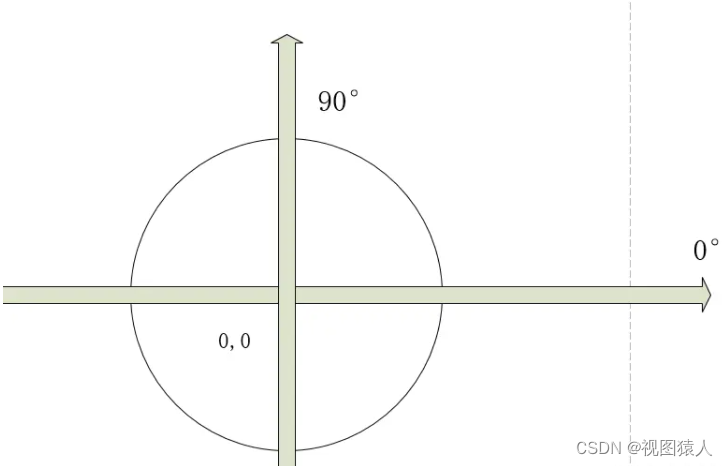
Qt之实现圆形进度条
在Qt自带的控件中,只有垂直进度条、水平进度条两种。 在平时做页面开发时,有些时候会用到圆形进度条,比如说:下载某个文件的下载进度。 展示效果,如下图所示: 实现这个功能主要由以下几个重点:…...

C# 图解教程 第5版 —— 第1章 C# 和 .NET 框架
文章目录 1.1 在 .NET 之前1.2 .NET 时代1.2.1 .NET 框架的组成1.2.2 大大改进的编程环境 1.3 编译成 CIL1.4 编译成本机代码并执行1.5 CLR1.6 CLI1.7 各种缩写1.8 C# 的演化1.9 C# 和 Windows 的演化(*) 1.1 在 .NET 之前 MFC(Microsoft Fou…...
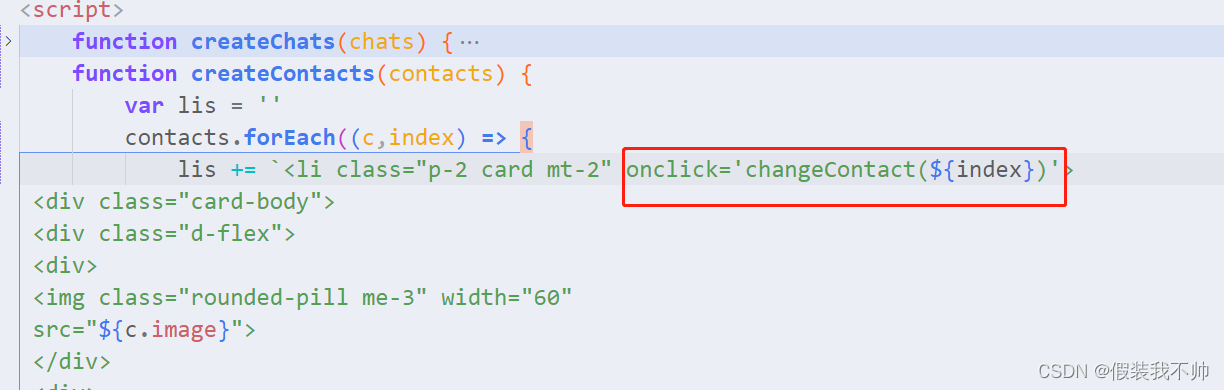
electronjs入门-聊天应用程序,与Electron.js通信
随着第一章中构建的应用程序,我们将开始将其与Electron框架中的模块集成,并以此为基础,以更实用的方式了解它们。 过程之间的通信 根据第二章中的解释,我们将发送每个进程之间的消息;具体来说联系人和聊天࿱…...
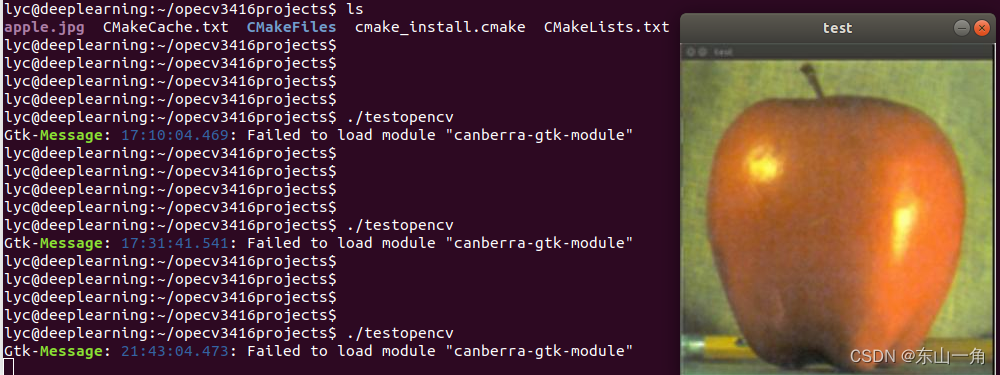
【自用】ubuntu 18.04 LTS安装opencv 3.4.16 + opencv_contrib 3.4.16
1.下载 opencv 3.4.16 opencv_contrib 3.4.16 其中,opencv_contrib解压后的多个文件夹复制到opencv内、合并 声明:尚未验证该方式是否可行 2.安装 参考博文: https://zhuanlan.zhihu.com/p/650792342 https://zhuanlan.zhihu.com/p/8719780…...
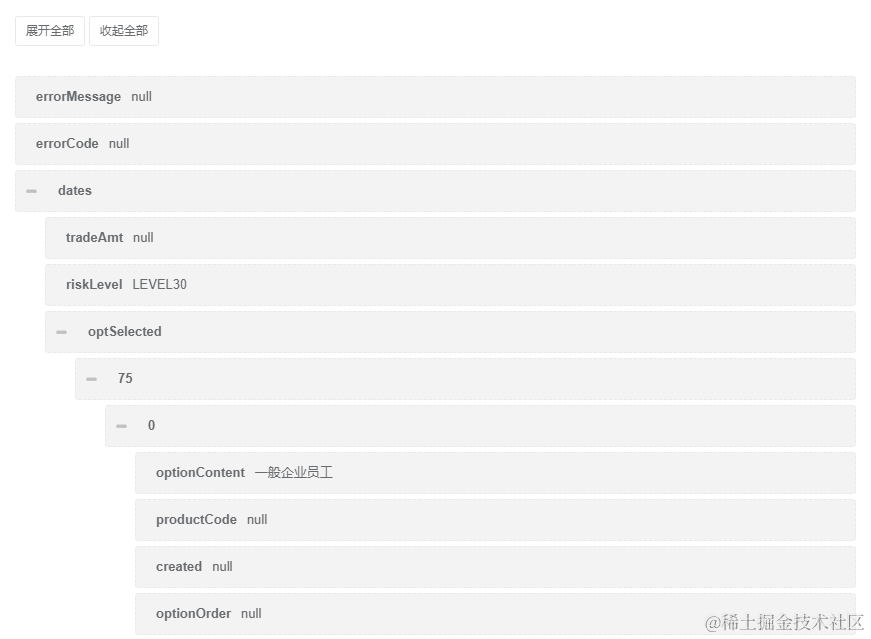
递归解析Json,实现生成可视化Tree+快速获取JsonPath | 京东云技术团队
内部平台的一个小功能点的实现过程,分享给大家: 递归解析Json,可以实现生成可视化Tree快速获取JsonPath。 步骤: 1.利用JsonPath读取根,获取JsonObject 2.递归层次遍历JsonObjec,保存结点信息 3.利用z…...

GraceUI相关的 知识
调试工具:UniApp提供了一些调试工具和插件,如uni-app-cli、调试器等,可以帮助你更好地定位和解决问题。同时,使用浏览器的开发者工具或模拟器的调试功能,可以更直观地观察页面效果和调试代码。 对于 GraceUI 的普通版本…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现,这取决于你是想在组件内部直接设置,还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法: 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...
