数字三角形加强版题解(组合计数+快速幂+逆元)
Description
一个无限行的数字三角形,第 i 行有 i 个数。第一行的第一个数是 1 ,其他的数满足如下关系:如果用 F[i][j] 表示第 i 行的第 j 个数,那么 F[i][j]=A∗F[i−1][j]+B∗F[i−1][j−1] (不合法的下标的数为 0 )。 当 A=2,B=3 时的数字三角形的前 5 行为: 1 2 3 4 12 9 8 36 54 27 16 96 216 216 81现在有 T 次询问,求 A=a,B=b 时数字三角形的第 n 行第 m 个数的值模 10^9+9 的结果。
Input
第一行为一个整数 T 。 接下一共 T 行,每行四个整数 a,b,n,m
Output
一共 T 行,每行一个整数,表示那个位置上的数的值。
Sample Input
2 2 3 3 3 3 1 4 1
Sample Output
9 27
Hint
n,t<=1e5;1<=m<=n; 0<=a,b<=1e9;
思路:
看例子:
1
A B
A^2 2*A*B B^2
A^3 3*A^2*B 3*A*B^2 B^3
我们可以看出答案是:
对于,分母我们利用费马小定理求逆元。
代码:
#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<string>
#include<cstring>
#include<cmath>
#include<ctime>
#include<algorithm>
#include<utility>
#include<stack>
#include<queue>
#include<vector>
#include<set>
#include<math.h>
#include<unordered_map>
#include<map>
using namespace std;
#define LL long long
const long long mod = 1e9 + 9;
const int N = 1e5 + 100;
LL xia[N];
LL quick(LL a, LL b, LL p)//根据a^(p-1)%p=1求a的逆元a^(p-2)%p;
{
LL res = 1;
while (b)
{
if (b & 1) res = (res * a) % p;
b >>= 1;
a = (a * a) % p;
}
return res;
}
LL seek(LL x, LL y)
{
LL e = 1;
while (y)
{
if (y & 1)
e = e * x % mod;
x = x * x % mod;
y = y >> 1;
}
return e;
}
int main()
{
int T;
LL a, b, n, m;
xia[0] = 1;
for (int i = 1; i <=1e5; i++)
xia[i] = (xia[i-1] * i) % mod;
scanf("%d", &T);
while (T--)
{
LL ans = 1;
scanf("%lld%lld%lld%lld", &a, &b, &n, &m);
ans = (ans*seek(a, n - m))%mod;
ans = (ans*seek(b, m-1))%mod;
ans = (ans * xia[n-1]) % mod;
ans = (ans * quick(xia[m-1], mod - 2, mod)) % mod;
ans= (ans * quick(xia[n-m], mod - 2, mod)) % mod;
printf("%lld\n",(ans % mod + mod) % mod);
}
return 0;
}
相关文章:
数字三角形加强版题解(组合计数+快速幂+逆元)
Description 一个无限行的数字三角形,第 i 行有 i 个数。第一行的第一个数是 1 ,其他的数满足如下关系:如果用 F[i][j] 表示第 i 行的第 j 个数,那么 F[i][j]A∗F[i−1][j]B∗F[i−1][j−1] (不合法的下标的数为 0 &a…...
MySQL:主从复制-基础复制(6)
环境 主服务器 192.168.254.1 从服务器(1)192.168.254.2 从服务器(2)192.168.253.3 我在主服务器上执行的操作会同步至从服务器 主服务器 yum -y install ntp 我们去配置ntp是需要让从服务器和我们主服务器时间同步 sed -i /…...

盒子模型的基础
盒子模型 边框(border) border可以设置元素的边框,边框分成三部分,边框的(粗细)边框的样式,边框的颜色 <style>div {width: 100px;height: 100px;border-width: 200;border-style: 边框…...
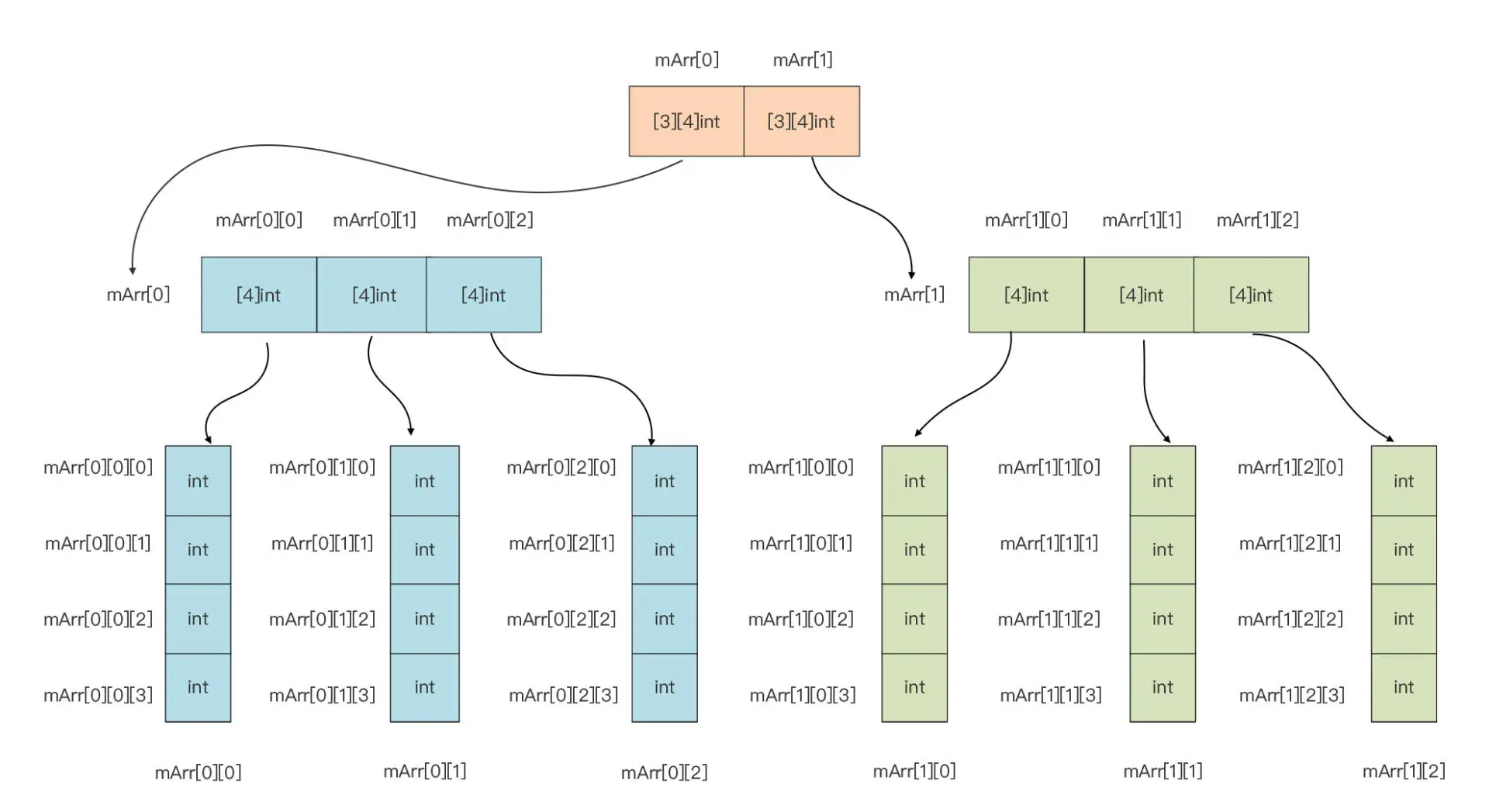
Go复合类型之数组类型
Go复合类型之数组 文章目录 Go复合类型之数组一、数组(Array)介绍1.1 基本介绍1.2 数组的特点 二、数组的声明与初始化2.1 数组声明2.2 常见的数据类型声明方法2.3 数组的初始化方式一:使用初始值列表初始化数组方法二:根据初始值个数自动推断数组长度方…...

rust闭包
一、闭包是什么 (一)闭包是什么 我们先来看看javascript中的闭包。 在函数外部无法读取函数内的局部变量。但是我们有时候需要得到函数内的局部变量,那么如何从外部读取局部变量?那就是在函数的内部,再定义一个函数。…...

通过位运算,实现单字段标识多个状态位
可能经常有如下这种需求: 需要一张表,来记录学员课程的通过与否. 课程数量不确定,往往很多,且会有变动,随时可能新增一门课. 这种情况下,在设计表结构时,一门课对应一个字段,就有些不合适, 因为不知道课程的具体数量,也无法应对后期课程的增加. 考虑只用一个状态标志位,利用位运…...

ALSA pcm接口的概念解释
PCM(数字音频)接口 PCM缩写: Pulse Code Modulation脉冲调制编码,我们理解为通过一定连续时间周期产生数字音频并带有音量样本的处理过程. 模拟信号被记录通过模拟到数字转换器,数字值(也就是某个特定时刻的音量值)获得来自ADC可以进一步处理,接下的图片展示的是个sine wavefor…...

logging的基本使用教程
logging的基本使用教程 一、简介: logging模块是Python的标准库,用于记录应用程序运行时的日志信息。使用logging模块可以帮助您在开发过程中调试代码、追踪问题和监控应用程序的运行状况。 二、使用教程 1、logging模块的基本使用方法: …...

ds套dp——考虑位置转移or值域转移:CF1762F
https://www.luogu.com.cn/problem/CF1762F 分析性质,就是我们选的数要么递增,要么递减(非严格)然后很明细是ds套dp, f i f_i fi 表示以 i i i 开头的答案然后考虑如何转移(ds套dp难点反而在转移而不是…...
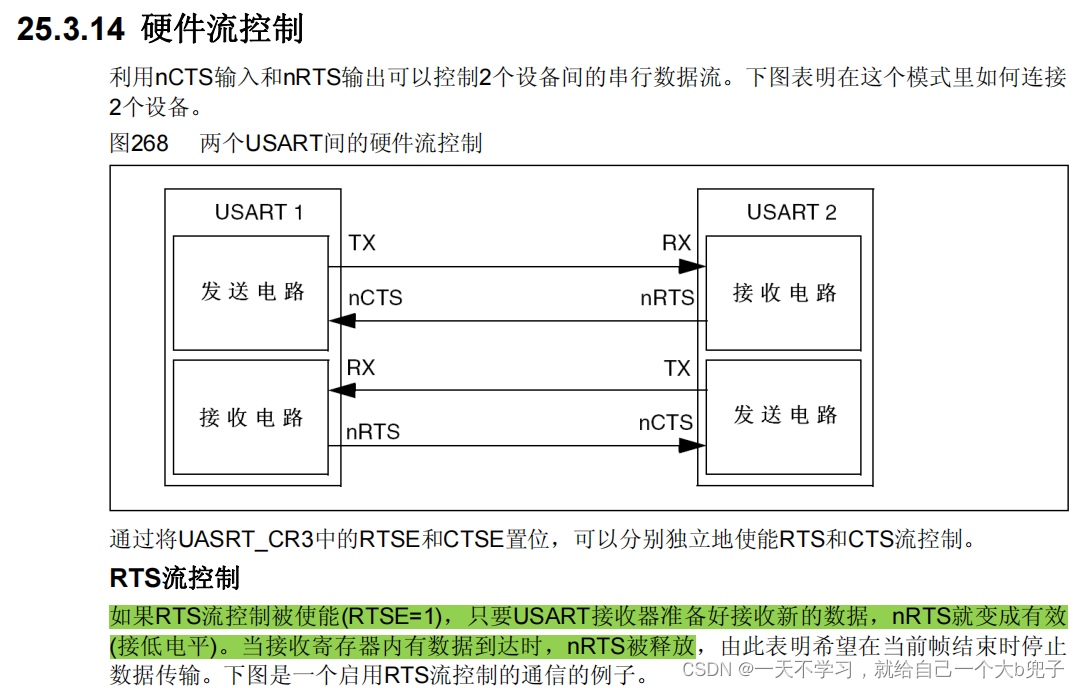
stm32的GPIO寄存器操作以及GPIO外部中断,串口中断
一、学习参考资料 (1)正点原子的寄存器源码。 (2)STM32F103最小系统板开发指南-寄存器版本_V1.1(正点) (3)STM32F103最小系统板开发指南-库函数版本_V1.1(正点&a…...
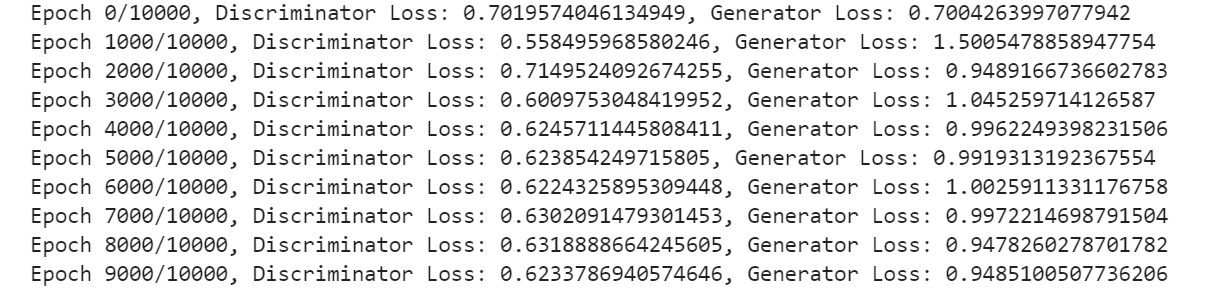
生成对抗网络入门案例
前言 生成对抗网络(Generative Adversarial Networks,简称GANs)是一种用于生成新样本的机器学习模型。它由两个主要组件组成:生成器(Generator)和判别器(Discriminator)。生成器尝试…...
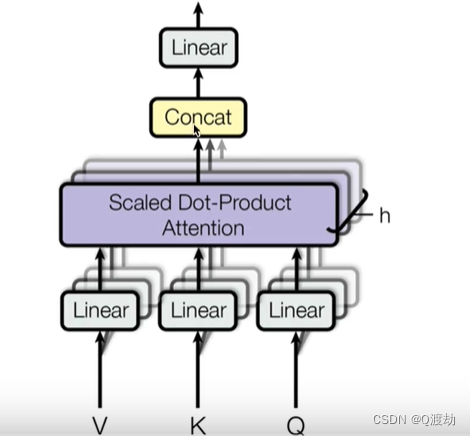
多头注意力机制
1、什么是多头注意力机制 从多头注意力的结构图中,貌似这个所谓的多个头就是指多组线性变换,但是并不是,只使用了一组线性变换层,即三个变换张量对 Q、K、V 分别进行线性变换,这些变化不会改变原有张量的尺寸…...
Qt + FFmpeg 搭建 Windows 开发环境
Qt FFmpeg 搭建 Windows 开发环境 Qt FFmpeg 搭建 Windows 开发环境安装 Qt Creator下载 FFmpeg 编译包测试 Qt FFmpeg踩坑解决方法1:换一个 FFmpeg 库解决方法2:把项目改成 64 位 后记 官方博客:https://www.yafeilinux.com/ Qt开源社区…...

[网鼎杯 2020 白虎组]PicDown python反弹shell proc/self目录的信息
[网鼎杯 2020 白虎组]PicDown - 知乎 这里确实完全不会 第一次遇到一个只有文件读取思路的题目 这里也确实说明还是要学学一些其他的东西了 首先打开环境 只存在一个框框 我们通过 目录扫描 抓包 注入 发现没有用 我们测试能不能任意文件读取 ?url../../../../etc/passwd …...
SDL2绘制ffmpeg解析的mp4文件
文章目录 1.FFMPEG利用命令行将mp4转yuv4202.ffmpeg将mp4解析为yuv数据2.1 核心api: 3.SDL2进行yuv绘制到屏幕3.1 核心api 4.完整代码5.效果展示6.SDL2事件响应补充6.1 处理方式-016.2 处理方式-02 本项目采用生产者消费者模型,生产者线程:使用ffmpeg将m…...

决策树C4.5算法的技术深度剖析、实战解读
目录 一、简介决策树(Decision Tree)例子: 信息熵(Information Entropy)与信息增益(Information Gain)例子: 信息增益比(Gain Ratio)例子: 二、算…...
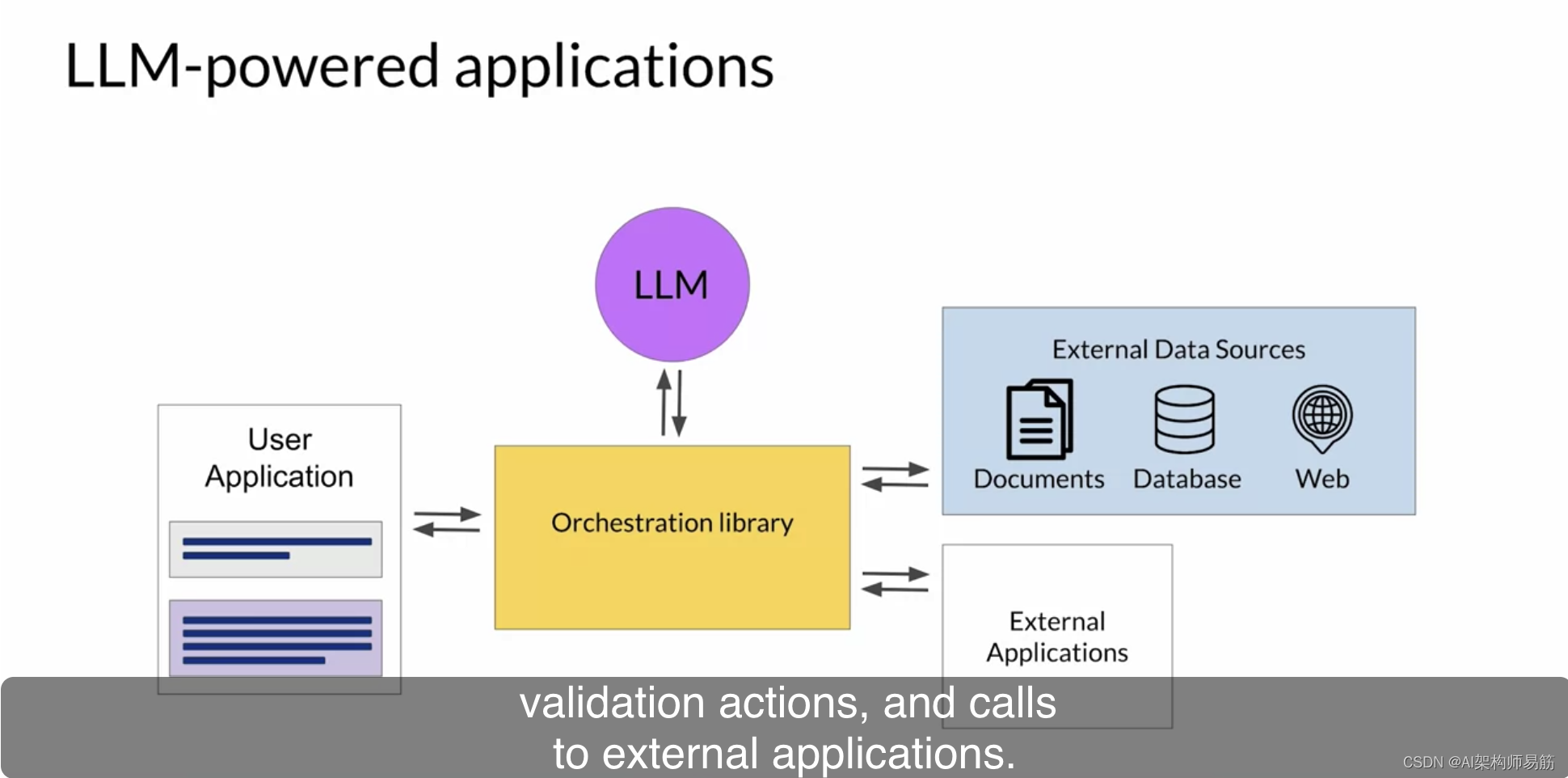
LLMs Python解释器程序辅助语言模型(PAL)Program-aided language models (PAL)
正如您在本课程早期看到的,LLM执行算术和其他数学运算的能力是有限的。虽然您可以尝试使用链式思维提示来克服这一问题,但它只能帮助您走得更远。即使模型正确地通过了问题的推理,对于较大的数字或复杂的运算,它仍可能在个别数学操…...
【12】c++设计模式——>单例模式练习(任务队列)
属性: (1)存储任务的容器,这个容器可以选择使用STL中的队列(queue) (2)互斥锁,多线程访问的时候用于保护任务队列中的数据 方法:主要是对任务队列中的任务进行操作 &…...
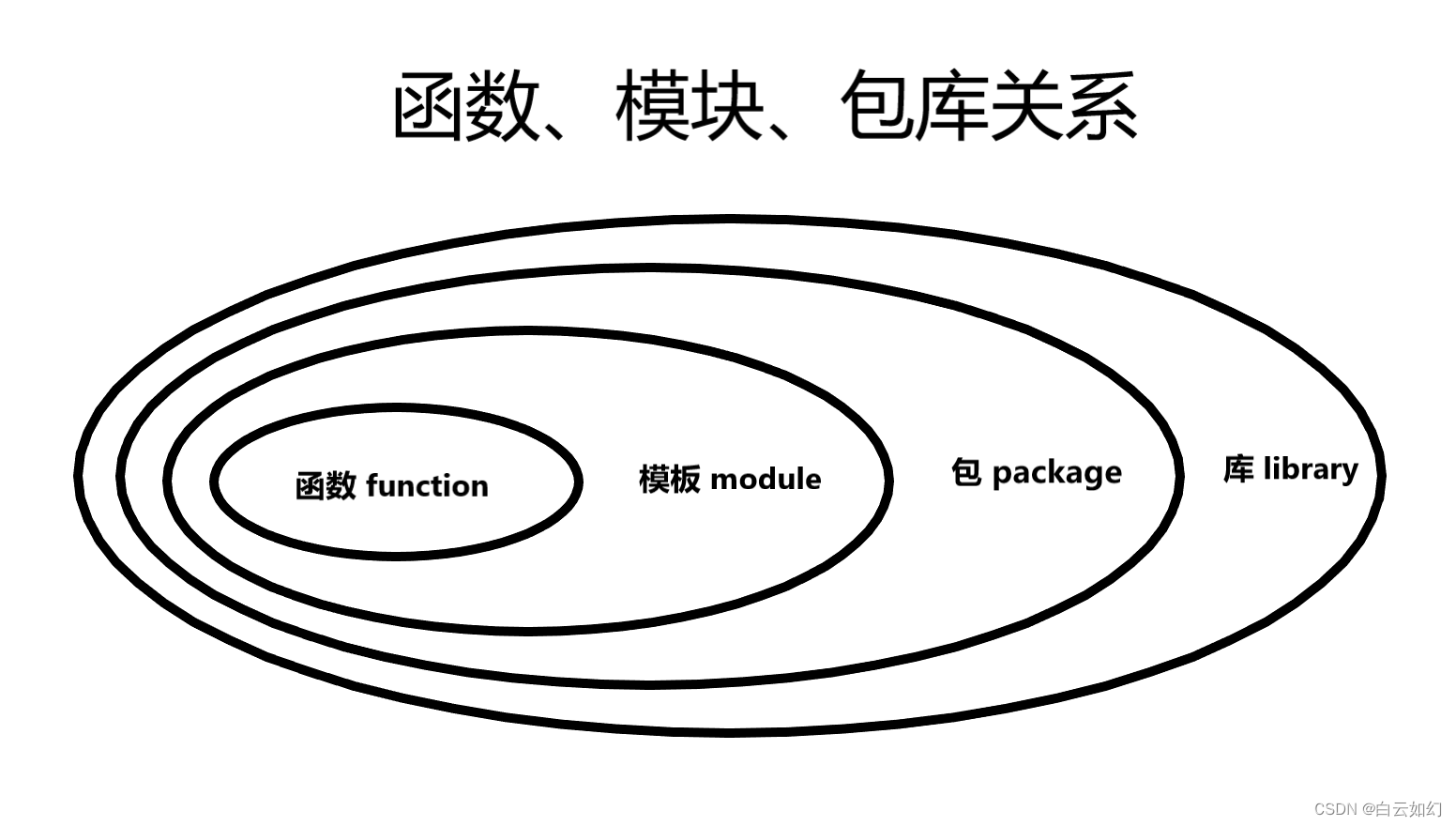
Python之函数、模块、包库
函数、模块、包库基础概念和作用 A、函数 减少代码重复 将复杂问题代码分解成简单模块 提高代码可读性 复用老代码 """ 函数 """# 定义一个函数 def my_fuvtion():# 函数执行部分print(这是一个函数)# 定义带有参数的函数 def say_hello(n…...

SQL创建与删除索引
索引创建、删除与使用: 1.1 create方式创建索引:CREATE [UNIQUE – 唯一索引 | FULLTEXT – 全文索引 ] INDEX index_name ON table_name – 不指定唯一或全文时默认普通索引 (column1[(length) [DESC|ASC]] [,column2,…]) – 可以对多列建立组合索引 …...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

STM32---外部32.768K晶振(LSE)无法起振问题
晶振是否起振主要就检查两个1、晶振与MCU是否兼容;2、晶振的负载电容是否匹配 目录 一、判断晶振与MCU是否兼容 二、判断负载电容是否匹配 1. 晶振负载电容(CL)与匹配电容(CL1、CL2)的关系 2. 如何选择 CL1 和 CL…...

解析奥地利 XARION激光超声检测系统:无膜光学麦克风 + 无耦合剂的技术协同优势及多元应用
在工业制造领域,无损检测(NDT)的精度与效率直接影响产品质量与生产安全。奥地利 XARION开发的激光超声精密检测系统,以非接触式光学麦克风技术为核心,打破传统检测瓶颈,为半导体、航空航天、汽车制造等行业提供了高灵敏…...

通过 Ansible 在 Windows 2022 上安装 IIS Web 服务器
拓扑结构 这是一个用于通过 Ansible 部署 IIS Web 服务器的实验室拓扑。 前提条件: 在被管理的节点上安装WinRm 准备一张自签名的证书 开放防火墙入站tcp 5985 5986端口 准备自签名证书 PS C:\Users\azureuser> $cert New-SelfSignedCertificate -DnsName &…...

【LeetCode】算法详解#6 ---除自身以外数组的乘积
1.题目介绍 给定一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O…...
