【剑指Offer】重建二叉树(递归+迭代)
重建二叉树
- 一、递归法
- 二、迭代法
题目链接
题目描述:
输入某二叉树的前序遍历和中序遍历的结果,请构建该二叉树并返回其根节点。
假设输入的前序遍历和中序遍历的结果中都不含重复的数字。
示例 1:

Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
Output: [3,9,20,null,null,15,7]
示例 2:
Input: preorder = [-1], inorder = [-1]
Output: [-1]
一、递归法
首先我们知道中序的左边就是该节点的左子树,中序的右边就是该节点的右子树,而确认根的顺序就需要靠前序。
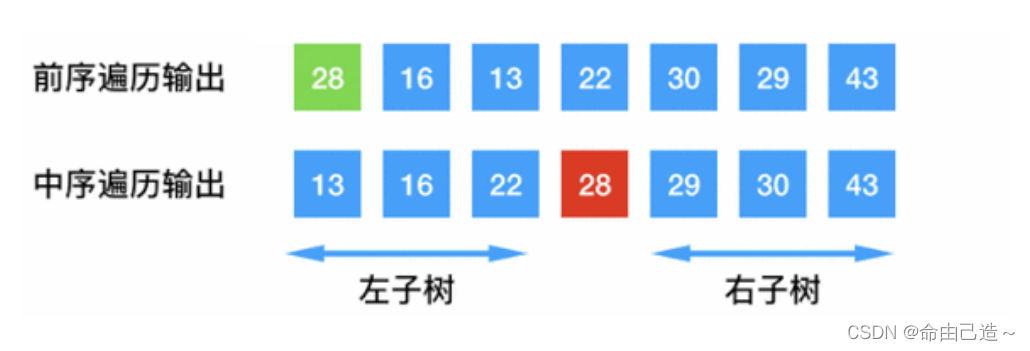
所以我们可以用一个变量pi记录前序遍历的位置,在中序中找到相同的元素,然后把它的左右区间递归下去。
这里注意如果要每次递归都需要遍历中序找到根,时间复杂度过高,所以我们可以在递归前先用哈希表映射根的位置。
代码如下
class Solution {
public:unordered_map<int, int> index;TreeNode* _bulidTree(vector<int>& pre, vector<int>& in, int& pi, int begin, int end){if (begin > end) return nullptr;int mid = index[pre[pi]];TreeNode* root = new TreeNode(pre[pi++]);root->left = _bulidTree(pre, in, pi, begin, mid - 1);root->right = _bulidTree(pre, in, pi, mid + 1, end);return root;}TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {int pi = 0;for (int i = 0; i < preorder.size(); i++){index[inorder[i]] = i;}return _bulidTree(preorder, inorder, pi, 0, preorder.size() - 1);}
};
二、迭代法
三种顺序的迭代法遍历:【数据结构】二叉树的非递归遍历
我们先假象一种情况,一棵树只有左子树的话,那么就相当于是一个单链表,那么它的前序遍历和中序遍历就刚好是反过来的。那么我们就可以使用栈来逆序存放,一旦遍历到最左下节点,这时候就该返回,开始弹栈,当我们发现弹栈的顺序和中序遍历不一致的时候,说明最后一个弹出来的节点有右子树。
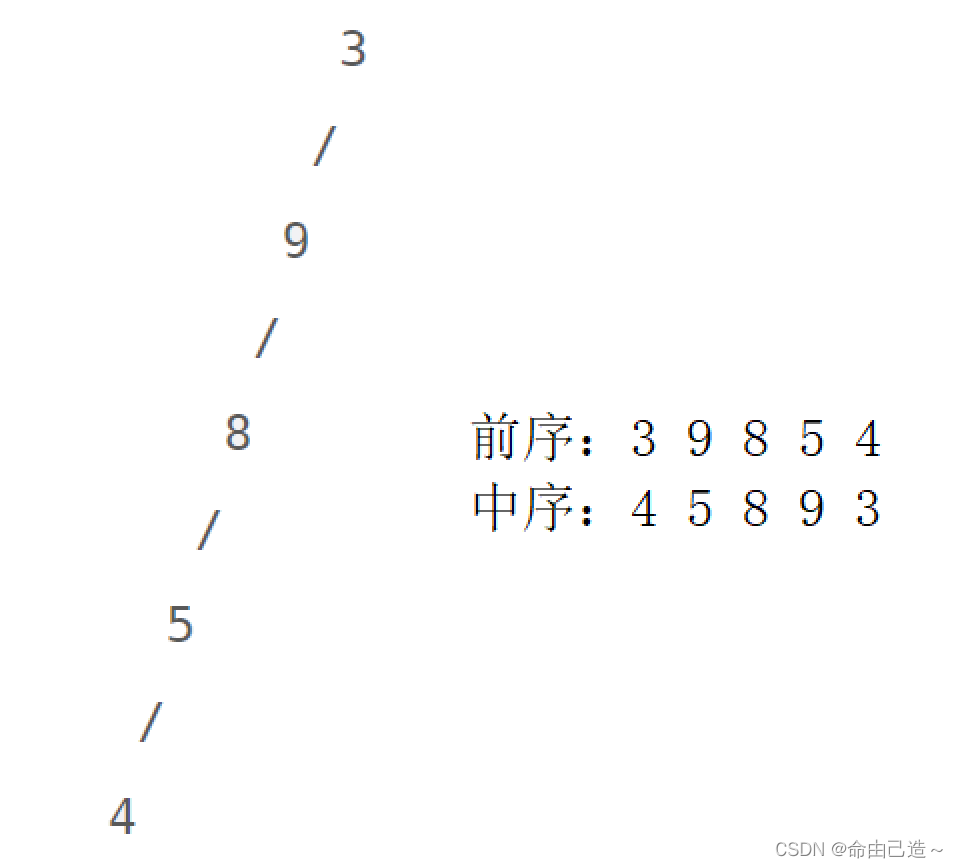
可以发现前序走完后出栈顺序刚好是中序遍历的结果,所以没有右子树。
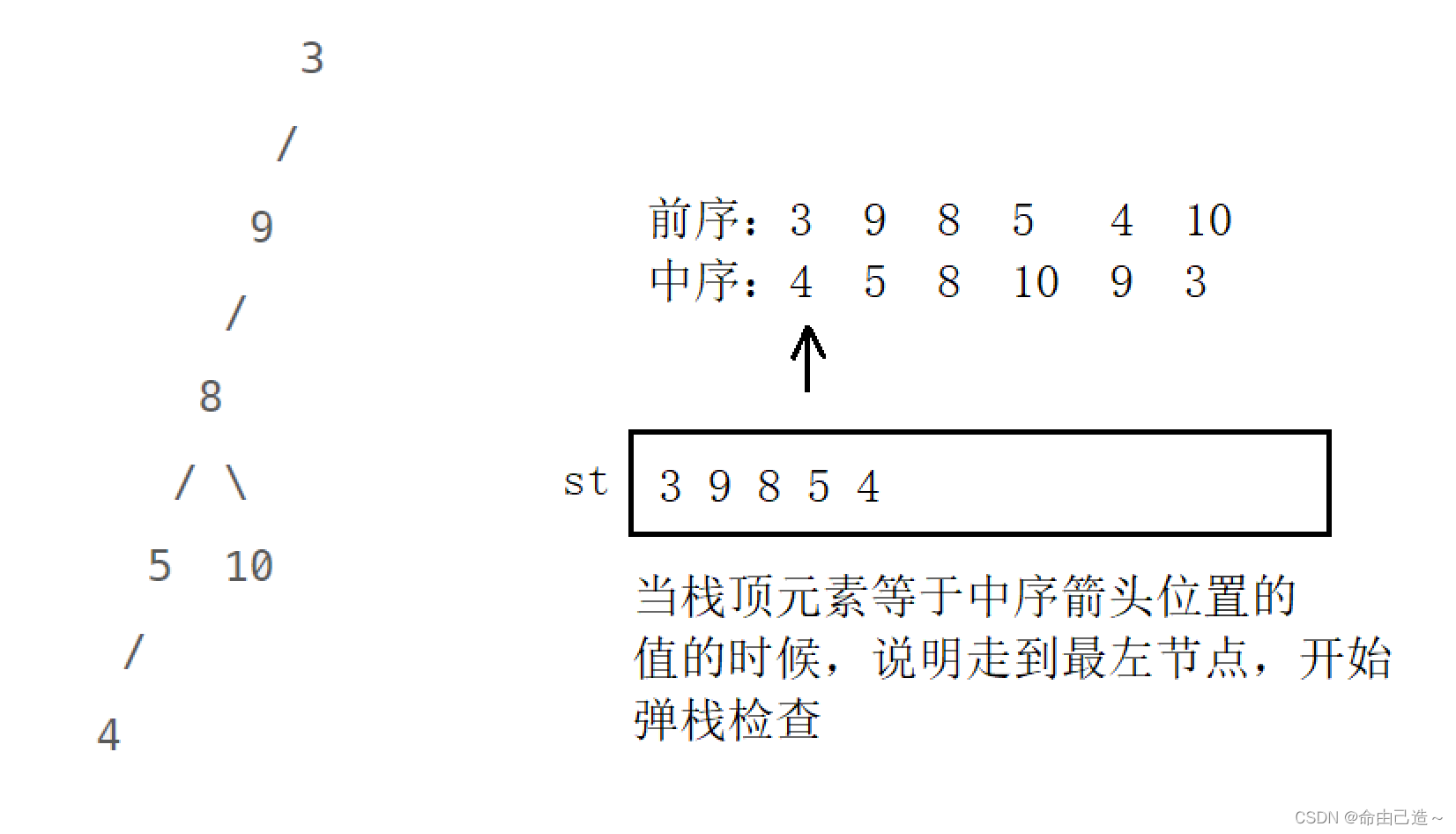
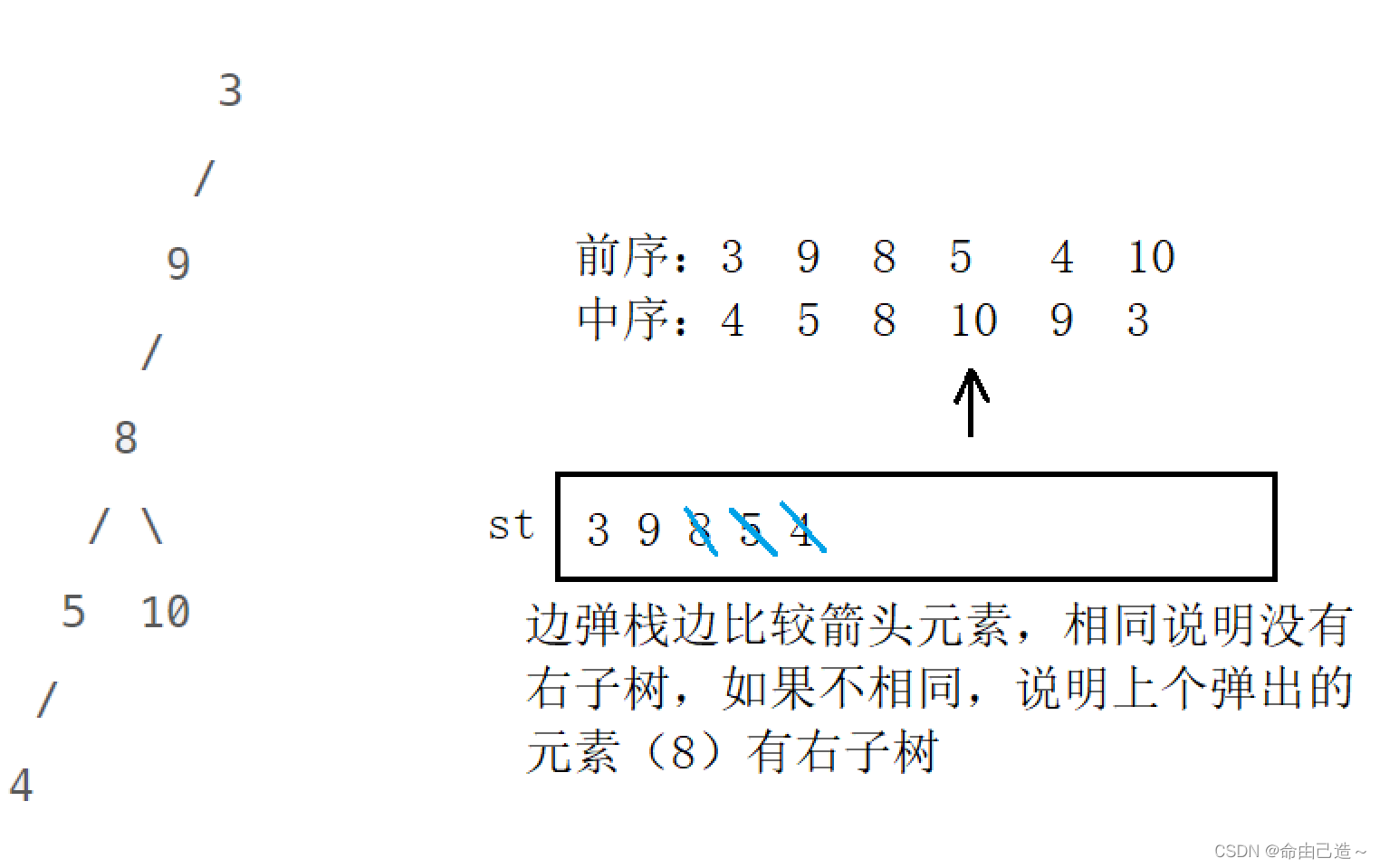
代码如下:
class Solution {
public:TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {if(preorder.empty()) return nullptr;stack<TreeNode*> st;int inorIndex = 0;TreeNode* root = new TreeNode(preorder[0]);st.push(root);for(int i = 1; i < preorder.size(); i++){TreeNode* node = st.top();if(node->val != inorder[inorIndex]){node->left = new TreeNode(preorder[i]);st.push(node->left);}else{while(!st.empty() && st.top()->val == inorder[inorIndex]){node = st.top();st.pop();inorIndex++;}node->right = new TreeNode(preorder[i]);st.push(node->right);}}return root;}
};
相关文章:

【剑指Offer】重建二叉树(递归+迭代)
重建二叉树一、递归法二、迭代法题目链接 题目描述: 输入某二叉树的前序遍历和中序遍历的结果,请构建该二叉树并返回其根节点。 假设输入的前序遍历和中序遍历的结果中都不含重复的数字。 示例 1: Input: preorder [3,9,20,15,7], inorder [9,3,15,…...

注解@Transactional 原理和常见的坑
这篇文章,会先讲述 Transactional 的 4 种不生效的 Case,然后再通过源码解读,分析 Transactional 的执行原理,以及部分 Case 不生效的真正原因1 项目准备下面是 DB 数据和 DB 操作接口:uidunameusex1张三女2陈恒男3楼仔…...

2023年全国最新交安安全员精选真题及答案4
百分百题库提供交安安全员考试试题、交安安全员考试预测题、交安安全员考试真题、交安安全员证考试题库等,提供在线做题刷题,在线模拟考试,助你考试轻松过关。 31.特种劳动防护用品必须具有“三证”,下列不属于“三证”的是&#…...
扬帆优配|半天翻倍,“蹭热点”翻车,前期“牛股”已近腰斩
周五上午,A股商场整体走低,多数职业板块和个股跌落,军工和核算机等板块逆势上涨,北向资金半天净卖出额约38亿元。 个股方面,昨夜公告被证监会立案查询的奥联电子股价再度大跌,盘中最贱价较近期高位已腰斩。…...

6 种易于上手的编程副业,每月赚取 1,000 多美元——没有废话
没有自由职业者或博客,也不需要前期费用。你们中的大多数人阅读这样的故事是希望其中的一些故事能帮助您赚更多的钱。好吧,几年前我还是同一个人。我希望尝试一些新的副业并赚点钱。其中一个视频建议我在网上写作,此后我写了很多技术文章。在…...
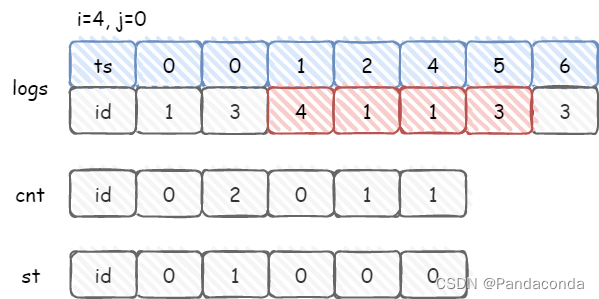
第九届蓝桥杯省赛 C++ B组 - 日志统计
✍个人博客:https://blog.csdn.net/Newin2020?spm1011.2415.3001.5343 📚专栏地址:蓝桥杯题解集合 📝原题地址:日志统计 📣专栏定位:为想参加蓝桥杯的小伙伴整理常考算法题解,祝大家…...

记一次服务器入侵事件的应急响应
0x01 事件背景 8月某日,客户官网被黑,需在特定时间内完成整改。为避免客户业务受到影响,实验室相关人员第一时间展开本次攻击事件的应急处理。 0x02 事件分析 网站源码被篡改,攻击者一定获取到了权限,那么接下来的思…...
)
作用域链查找机制(回顾)
全局 / 私有变量作用域的概念作用域链 scopeChain 的概念作用域链 scopeChain 的形成函数执行步骤作用域链查找机制 全局 / 私有变量 全局变量:在全局上下文EC(G)中的全局变量对象VO(G)中,存储的变量 私有变量:在函数执行形成的私有上下文EC(XXX)中的变…...

前端基础之HTML扫盲
文章目录一. 第一个HTML程序1. 创建一个HTML文件并运行2. HTML的基本结构二. HTML常见标签1. 注释标签2. 标题标签3. 段落标签4. 换行标签5. 格式化标签6. 图片标签7. 超链接标签8. 表格标签9. 列表标签10. 表单标签10.1 input标签10.2 select标签10.3 textarea标签11. 无语义标…...

大规模食品图像识别:T-PAMI 2023论文解读
美团基础研发平台视觉智能部与中科院计算所展开科研课题合作,共同构建大规模数据集Food2K,并提出渐进式区域增强网络用于食品图像识别,相关研究成果已发表于T-PAMI 2023。本文主要介绍了数据集特点、方法设计、性能对比,以及基于该…...

【java】Spring Cloud --Spring Cloud Alibaba RocketMq 异步通信实现
文章目录介绍RocketMQ特点Spring Cloud StreamWindow搭建部署RocketMQ下载启动NameServer服务启动Broker服务示例创建 RocketMQ 消息生产者创建 RocketMQ 消息消费者使用示例示例关联项目运行示例测试介绍 RocketMQ 是一款开源的分布式消息系统,基于高可用分布式集…...
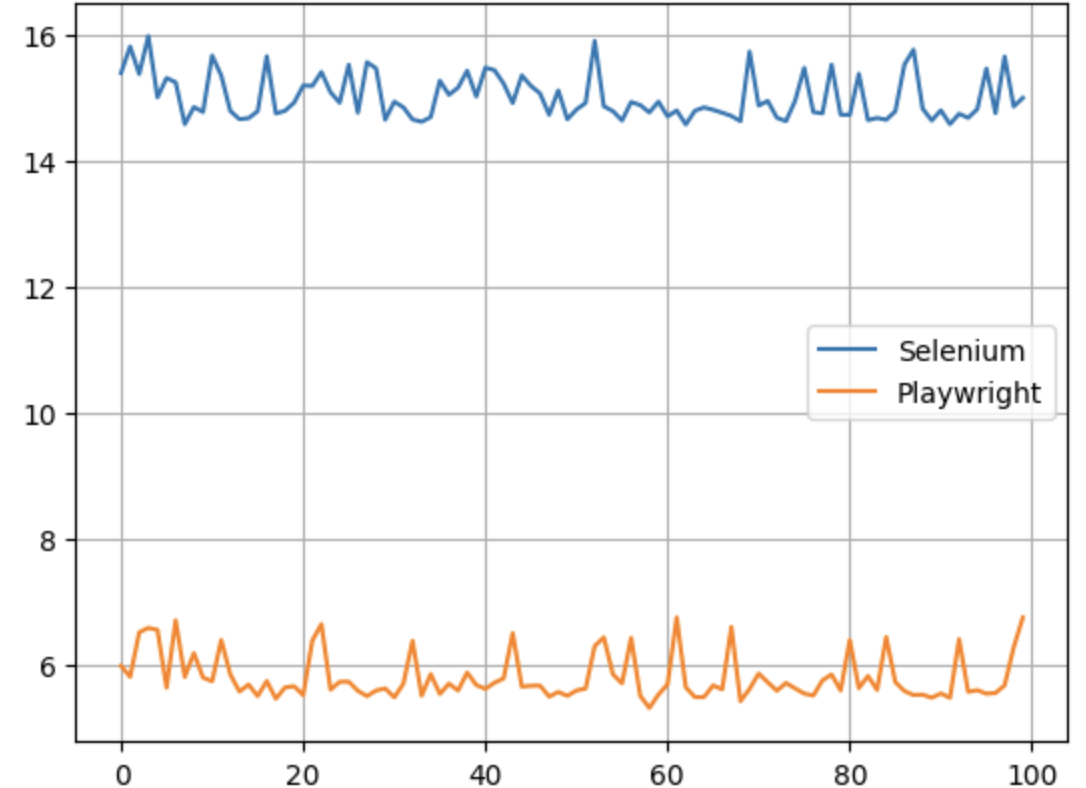
玫瑰花变蚊子血,自动化无痕浏览器对比测试,新贵PlayWright Vs 老牌Selenium,基于Python3.10
也许每一个男子全都有过这样的两个女人,至少两个。娶了红玫瑰,久而久之,红的变了墙上的一抹蚊子血,白的还是床前明月光;娶了白玫瑰,白的便是衣服上沾的一粒饭黏子,红的却是心口上一颗朱砂痣。–…...

Spring Cloud入门篇 Hello World | Spring Cloud 1
一、专栏说明 Spring Cloud是一系列框架的有序集合。它利用Spring Boot的开发便利性巧妙地简化了分布式系统基础设施的开发,如:服务发现/注册、配置中心、消息总线、负载均衡、断路器、数据监控等,都可以用Spring Boot的开发风格做到一键启动和部署。 本文主要介绍Spring C…...

C++学习笔记-数据结构
结构 是C中另一种用户自定义的可用数据类型,允许存储不同类型的数据项。 C/C 数组允许定义可存储相同类型数据项的变量,但是结构是 C 中另一种用户自定义的可用的数据类型,它允许存储不同类型的数据项。 结构用于表示一条记录,假…...

【C++的OpenCV】第五课-OpenCV图像常用操作(二):OpenCV的基本绘图、平滑滤波(模糊)处理
让我们继续一、OpenCV基本绘图1.1 OpenCV关于绘图的操作1.1.1 cv::Point()1.1.2 cv::Scalar()1.1.3 cv::line()画线1.1.4 cv::rectangle()画矩形1.1.5 cv::circle()画圆二、图像的平滑滤波处理2.1 概念2.2 OpenCV关于图像模糊的操作2.2.1 常用滤波器的分类2.2.2 各种滤波方法具…...

[SSD固态硬盘技术 19] 谁是数据的守护神? 盘内RAID1/RAID5图文详解_盘内数据冗余保护
版权声明: 付费作品,禁止转载前言提到冗余保护,最容易想到的就是RAID(Redundant Arrays of Independent Disks) , 独立冗余磁盘阵列。它是一种把多块独立的物理硬盘按不同方式组合形成一个硬盘组,以此提供比单个硬盘更高的存储性能…...

linux相对于windows环境为啥相对来说更加具有安全性
linux相对于windows环境为啥相对来说更加具有安全性 文章目录linux相对于windows环境为啥相对来说更加具有安全性前言一、linux不需要防病毒软件1.1Linux 桌面的恶意软件很少见1.2Linux 的软件安装更安全1.3Linux 保护自己免受恶意软件的侵害1.4杀毒效果存疑1.5Linux 良好的安全…...

iOS开发笔记之九十七——关于Restful API的一些总结
*****阅读完此文,大概需要3分钟******一、什么是 Restful API?Restful(Representational State Transfer表现层状态转换)是目前最流行的接口设计规范。Restful API 是一种设计风格(是设计风格而不是标准)&a…...

Linux系统Nginx下载和安装
文章目录golang学习面试网站Linux启动nginx参考Linux启动nginx版权声明:本文为博主原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。 本文链接:https://blog.csdn.net/weixin_36755535/article/details/110…...

交叉编译 acl
交叉编译 acl 概述 访问控制列表(Access Control Lists,ACL)是应用在路由器接口的指令列表。在 Linux 系统中,ACL 用于设定用户针对文件的权限,而不是在交换路由器中用来控制数据访问的功能(类似于防火墙…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

PHP 8.5 即将发布:管道操作符、强力调试
前不久,PHP宣布了即将在 2025 年 11 月 20 日 正式发布的 PHP 8.5!作为 PHP 语言的又一次重要迭代,PHP 8.5 承诺带来一系列旨在提升代码可读性、健壮性以及开发者效率的改进。而更令人兴奋的是,借助强大的本地开发环境 ServBay&am…...
