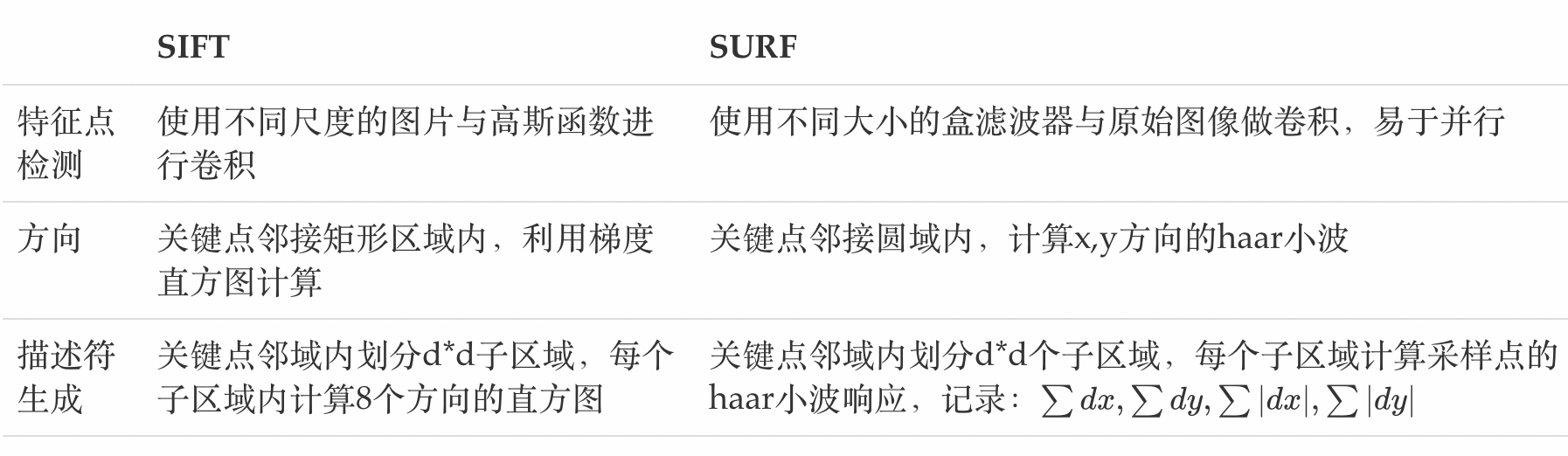
OpenCV 15(SIFT/SURF算法)
一、SIFT
Harris和Shi-Tomasi角点检测算法,这两种算法具有旋转不变性,但不具有尺度不变性,以下图为例,在左侧小图中可以检测到角点,但是图像被放大后,在使用同样的窗口,就检测不到角点了。

尺度不变特征转换即SIFT (Scale-invariant feature transform)。它用来侦测与描述影像中的局部性特征,它在空间尺度中寻找极值点,并提取出其位置、尺度、旋转不变量,此算法由 David Lowe在1999年所发表,2004年完善总结。应用范围包含物体辨识、机器人地图感知与导航、影像缝合、3D模型建立、手势辨识、影像追踪和动作比对等领域。
Lowe将SIFT算法分解为如下四步:

(1)建立高斯查分金字塔:搜索所有尺度上的图像位置。通过高斯差分函数来识别潜在的对于尺度和旋转不变的关键点。
在不同的尺度空间是不能使用相同的窗口检测极值点,对小的关键点使用小的窗口,对大的关键点使用大的窗口,为了达到上述目的,我们使用尺度空间滤波器。
高斯核是唯一可以产生多尺度空间的核函数。-《Scale-space theory: A basic tool for analysing structures at different scales》。 近处清晰,远处模糊
一个图像的尺度空间L(x,y,σ),定义为原始图像I(x,y)与一个可变尺度的2维高斯函数G(x,y,σ)卷积运算 ,即:

σ是尺度空间因子,它决定了图像的模糊的程度。在大尺度下(σ值大)表现的是图像的概貌信息,在小尺度下(σ值小)表现的是图像的细节信息。

下面我们构建图像的高斯金字塔,它采用高斯函数对图像进行模糊以及降采样处理得到的,整个流程如下图所示:

- 高斯金字塔构建过程中,首先将图像扩大一倍,在扩大的图像的基础之上构建高斯金字塔,然后对该尺寸下图像进行高斯模糊,几幅模糊之后的图像集合构成了一个Octave;
- 对该Octave下的最模糊的一幅图像进行下采样的过程,长和宽分别缩短一倍,图像面积变为原来四分之一。这幅图像就是下一个Octave的初始图像,在初始图像的基础上完成属于这个Octave的高斯模糊处理;
- 以此类推完成整个算法所需要的所有Octave构建,这样这个高斯金字塔就构建出来了
利用LoG(高斯拉普拉斯方法),即图像的二阶导数,可以在不同的尺度下检测图像的关键点信息,从而确定图像的特征点。但LoG的计算量大,效率低。所以我们通过两个相邻高斯尺度空间的图像的相减,得到DoG(高斯差分)来近似LoG。
为了计算DoG我们构建高斯差分金字塔,该金字塔是在上述的高斯金字塔的基础上构建而成的,建立过程是:在高斯金字塔中每个Octave中相邻两层相减就构成了高斯差分金字塔。如下图所示:

高斯差分金字塔的第1组第1层是由高斯金字塔的第1组第2层减第1组第1层得到的。以此类推,逐组逐层生成每一个差分图像,所有差分图像构成差分金字塔。概括为DOG金字塔的第o组第l层图像是有高斯金字塔的第o组第l+1层减第o组第l层得到的。后续Sift特征点的提取都是在DOG金字塔上进行的。
总结:
先用高斯核进行卷积,得到高斯金字塔 --》 差分卷积核
(2)极值点精确定位
在 DoG 搞定之后,就可以在不同的尺度空间中搜索局部最大值了。对于图像中的一个像素点而言,它需要与自己周围的 8 邻域,以及尺度空间中上下两层中的相邻的 18(2x9)个点相比。如果是局部最大值(26个点),它就可能是一个关键点。基本上来说关键点是图像在相应尺度空间中的最好代表。如下图所示:

在离散空间中寻找到的极值点并不一定是真正的极值点我们用离散值插值的方式,将离散空间转换为连续空间,得到更加准确的极值点。同时去除低对比度的关键点和不稳定的边缘响应点。

(3)关键点方向确定
经过上述两个步骤,图像的关键点就完全找到了,这些关键点具有尺度不变性。为了实现旋转不变性,还需要为每个关键点分配一个方向角度,也就是根据检测到的关键点所在高斯尺度图像的邻域结构中求得一个方向基准。
对于任一关键点,我们采集其所在高斯金字塔图像以r为半径的区域内所有像素的梯度特征(幅值和幅角),半径r为:
![]()
其中σ是关键点所在octave的图像的尺度,可以得到对应的尺度图像。
梯度的幅值和方向的计算公式为:


关键点的方向,并不是关键点的梯度方向,而是统计关键点邻域内所有点的梯度方向,将0-360度分为8个方向,每45度一个方向。形成的8个方向形成方向柱状图。

峰值代表关键点方向,大于峰值80%的作为辅方向。
辅方向对特征点匹配的稳定性非常重要
(4)关键点描述
为了保证特征点的旋转不变性,以特征点为中心,将坐标轴旋转为关键点的主方向,如下图所示:

取特征点周围8*8的像素进行梯度方向统计和高斯加权(蓝色圆圈代表高斯加权范围)。每4*4窗口生成8个方向,这样就生成了2*2*8的向量作为特征点的数学描述。

SIFT算法采用4*4*8共128维向量作为特征点的描述子。最后通过描述子的欧式距离进行特征点匹配。

SIFT在图像的不变特征提取方面拥有无与伦比的优势,但并不完美,仍然存在实时性不高,有时特征点较少,对边缘光滑的目标无法准确提取特征点等缺陷,自SIFT算法问世以来,人们就一直对其进行优化和改进,其中最著名的就是SURF算法。
sift = cv.xfeatures2d.SIFT_create() 实例化sift
kp,des = sift.detectAndCompute(gray,None) 检测关键点并计算参数:
- gray: 进行关键点检测的图像,注意是灰度图像
返回:
- kp: 关键点信息,包括位置,尺度,方向信息
- des: 关键点描述符,每个关键点对应128个梯度信息的特征向量
将关键点检测结果绘制在图像上
cv.drawKeypoints(image, keypoints, outputimage, color, flags)
- image: 原始图像
- keypoints:关键点信息,将其绘制在图像上
- outputimage:输出图片,可以是原始图像
- color:颜色设置,通过修改(b,g,r)的值,更改画笔的颜色,b=蓝色,g=绿色,r=红色。
- flags:绘图功能的标识设置
- cv2.DRAW_MATCHES_FLAGS_DEFAULT:创建输出图像矩阵,使用现存的输出图像绘制匹配对和特征点,对每一个关键点只绘制中间点
- cv2.DRAW_MATCHES_FLAGS_DRAW_OVER_OUTIMG:不创建输出图像矩阵,而是在输出图像上绘制匹配对
- cv2.DRAW_MATCHES_FLAGS_DRAW_RICH_KEYPOINTS:对每一个特征点绘制带大小和方向的关键点图形
- cv2.DRAW_MATCHES_FLAGS_NOT_DRAW_SINGLE_POINTS:单点的特征点不被绘制
import cv2 as cv
import numpy as np
import matplotlib.pyplot as plt
# 1 读取图像
img = cv.imread('./image/tv.jpg')
gray= cv.cvtColor(img,cv.COLOR_BGR2GRAY)
# 2 sift关键点检测
# 2.1 实例化sift对象
sift = cv.xfeatures2d.SIFT_create()# 2.2 关键点检测:kp关键点信息包括方向,尺度,位置信息,des是关键点的描述符
kp,des=sift.detectAndCompute(gray,None)
# 2.3 在图像上绘制关键点的检测结果
cv.drawKeypoints(img,kp,img,flags=cv.DRAW_MATCHES_FLAGS_DRAW_RICH_KEYPOINTS)
# 3 图像显示
plt.figure(figsize=(8,6),dpi=100)
plt.imshow(img[:,:,::-1]),plt.title('sift检测')
plt.xticks([]), plt.yticks([])
plt.show()
二、SURF
使用 SIFT 算法进行关键点检测和描述的执行速度比较慢, 需要速度更快的算法。 2006 年 Bay提出了 SURF 算法,是SIFT算法的增强版,它的计算量小,运算速度快,提取的特征与SIFT几乎相同,将其与SIFT算法对比如下:
相关文章:

OpenCV 15(SIFT/SURF算法)
一、SIFT Harris和Shi-Tomasi角点检测算法,这两种算法具有旋转不变性,但不具有尺度不变性,以下图为例,在左侧小图中可以检测到角点,但是图像被放大后,在使用同样的窗口,就检测不到角点了。 尺度…...
)
前端二维码图片解析图片识别/网络图片解析成链接/图片网络链接转本地链接(Js/Vue/Jquery)
注:需要用到canvas/jsqr/jquery! 1、远程图片链接本地化 页面: <!-- 识别二维码用的 canvas--> <canvas class"canvas" ref"canvas" style"display: none"></canvas> 1.创建图片 get2: fu…...
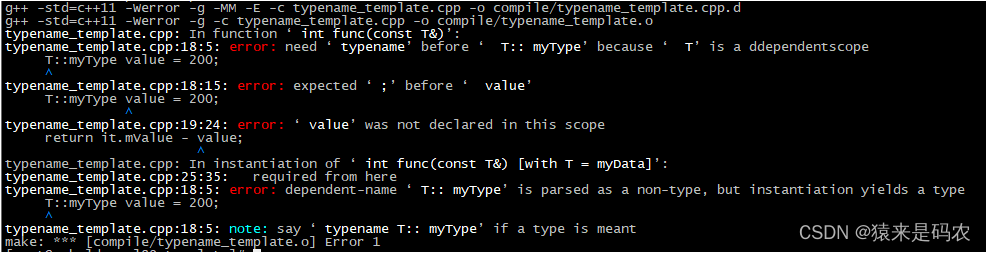
模板中的依赖类型使用 --- typename
依赖类型,顾名思义就是依赖于模板参数的类型,在使用这种类型时,必须使用 typename,否则编译器是无法知道是在使用类型,还是类的成员(因为类的静态成员的使用方法也是T::xxx,这跟某个类中的类型的…...
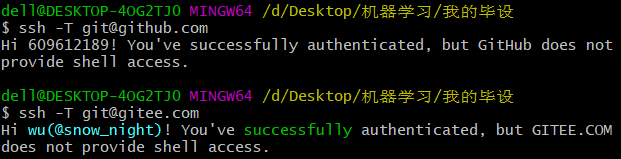
git 同时配置 gitee github
git 同时配置 gitee github 1、 删除C:\Users\dell\.ssh目录。 在任意目录右击——》Git Bash Here,打开Git Bash窗口,下方命令在Git Bash窗口输入。 2、添加git全局范围的用户名和邮箱 git config --global user.email "609612189qq.com" …...

2023.10.8 面试
面试工作1年的程序员 看到生涩才入职场不久的面试者,为人也相对诚恳的模样,我对此是很欣赏的态度。 因为完全看到了自己毕业1年时的场景。 简历上写的事情,讨论起来,描述不清楚,为此感到遗憾,因我本人也会…...

【前端】js实现队列功能 先进后出 先进先出 等
也可以定义一个定时器 不断的去取队列 执行任务 用一个flag定义队列正在执行中, 如果没有执行 则定时器不断的去调用队列,(因为会随时添加一个任务到队列中) 队列任务结束后 自动取下一个队列 也可以边加队列 边取 队列定义 function Queue() {//初始化队列(使用…...

07.数据持久化之文件操作
1. 文件操作 计算机的文件,就是存储在某种 长期储存设备 上的一段 数据 长期存储设备包括:硬盘、U 盘、移动硬盘、光盘… 文本文件和二进制文件 文本文件 可以使用 文本编辑软件 查看本质上还是二进制文件例如:python 的源程序 二进制文件…...
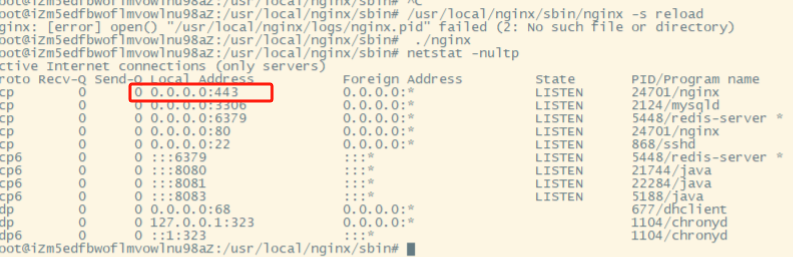
nginx开启https配置之后网页无法访问问题处理
背景说明 最近新购服务器部署nginx之后按照之前的方式部署前端项目并配置https之后访问页面显示:无法访问.新的服务器ECS系统和之前相同,nginx安装方式也相同,nginx配置方式也是相同.但是访问还是显示无法访问.下面简单记录一下问题处理过程. 处理过程 1.https访问之后无法访问…...
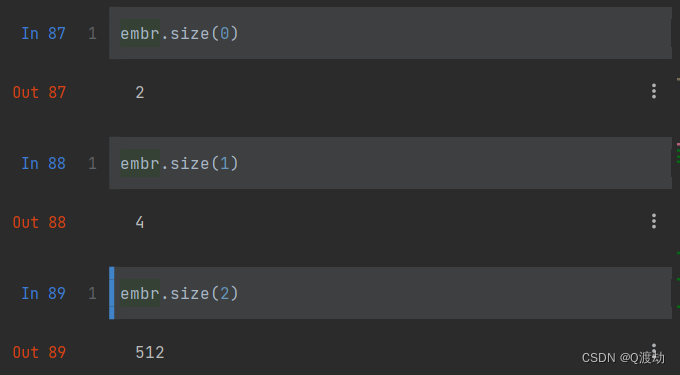
文本嵌入层
目录 1、文本嵌入层的作用 2、代码演示 3、构建Embeddings类来实现文本嵌入层 1、文本嵌入层的作用 无论是源文本嵌入层还是目标文本嵌入,都是为了将文本词汇中的数字表示转变为向量表示,希望在这样的高维空间中捕捉词汇之间的关系 2、代码演示 Emb…...
如何搭建自动化测试框架
关于测试框架的好处,比如快速回归提高测试效率,提高测试覆盖率等这里就不讨论了。这里主要讨论自动化框架包含哪些内容,以及如何去设计一个测试框架。 1. 什么是自动化测试框架? 它是由一个或多个自动化测试基础模块、自动化测试…...
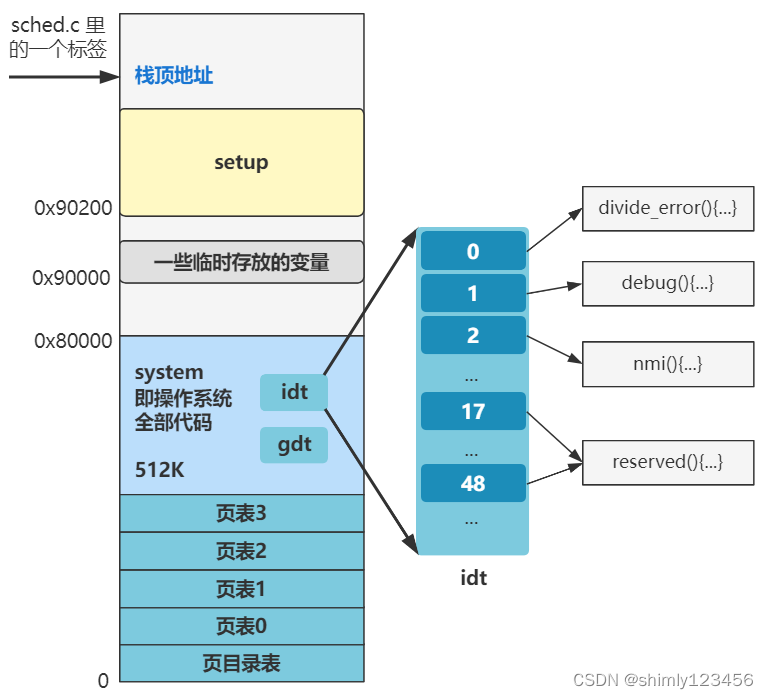
抄写Linux源码(Day17:你的键盘是什么时候生效的?)
回忆我们需要做的事情: 为了支持 shell 程序的执行,我们需要提供: 1.缺页中断(不理解为什么要这个东西,只是闪客说需要,后边再说) 2.硬盘驱动、文件系统 (shell程序一开始是存放在磁盘里的,所以需要这两个东…...

在原生html中使用less
引入less <link rel"stylesheet/less" href"./lessDemo.less" /><script src"./js/less.min.js"></script> less.min.js文件下载地址:https://github.com/less/less.js 注意:less文件在前,js文件在后…...
【Qt】顶层窗口和普通窗口区别以及用法
区别 在Qt项目开发中,经常会用到窗体控件用于显示及数据操作和其他交互等。 但,窗体分为顶层窗口(Top-level Window)和普通窗口(Regular Window)。 他们之间是有区别的,包括在项目实际中的用法…...
qt开发从入门到实战2
以下是本人学习笔记 原视频:最新QT从入门到实战完整版|传智教育 qt开发从入门到实战1 练习示例 设计一个按钮,点击时弹出新窗口,再次点击时新窗口关闭 // exerciseQWidget* second_window new QWidget();QPushButton* btn3 new QPushBu…...
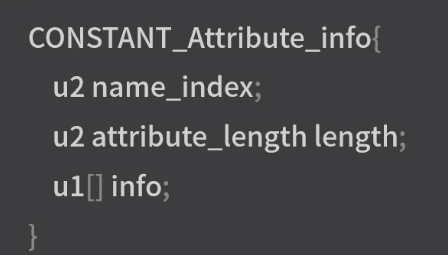
Android---字节码层面分析Class类文件
Java 提供了一种可以在所有平台上都能使用的一种中间代码---字节码文件(.class文件)。有了字节码,无论是那个平台只要安装了虚拟机都可以直接运行字节码文件。有了虚拟机,解除了 java 虚拟机与 java 代码之间的耦合。 Java 虚拟机当初被设计出来时就不单…...
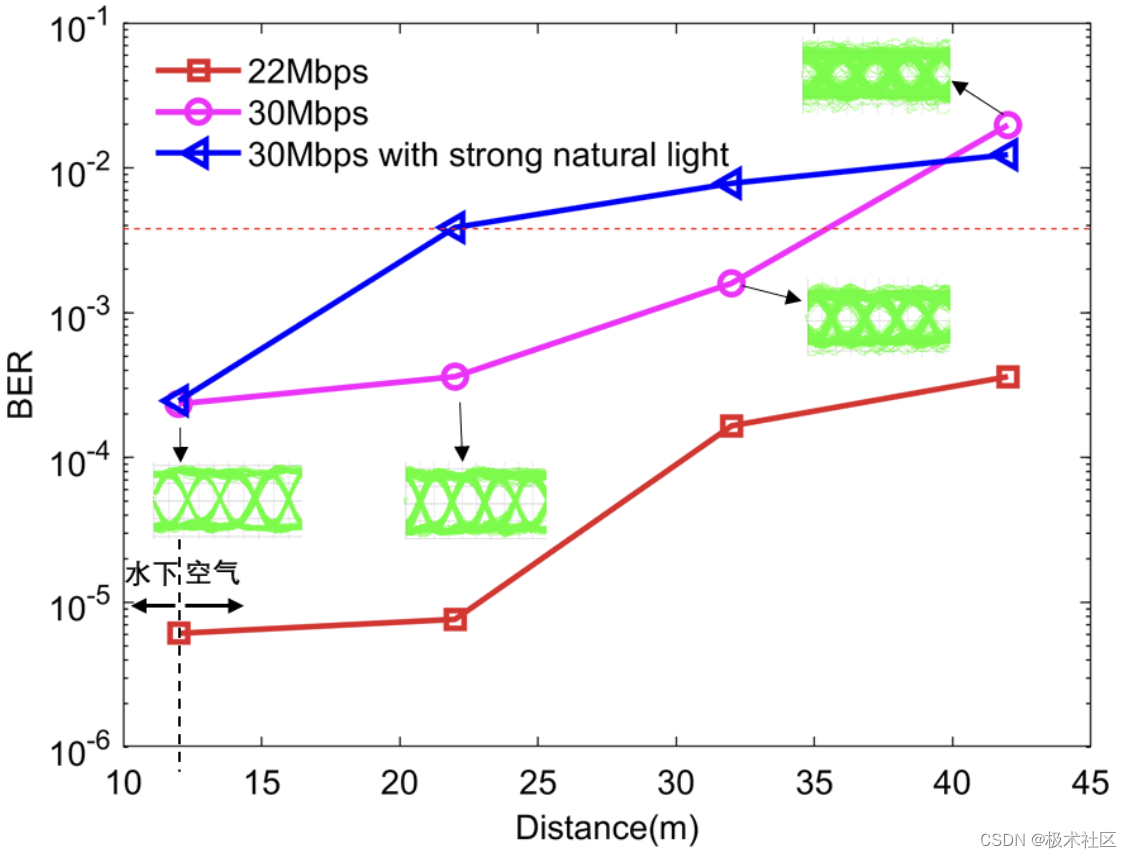
【2023研电赛】东北赛区一等奖作品:基于FPGA的小型水下无线光通信端机设计
本文为2023年第十八届中国研究生电子设计竞赛东北赛区一等奖作品分享,参加极术社区的【有奖活动】分享2023研电赛作品扩大影响力,更有丰富电子礼品等你来领!,分享2023研电赛作品扩大影响力,更有丰富电子礼品等你来领&a…...

JWT授权为啥要在 Authorization标头里加个Bearer 呢
这是因为 W3C 的 HTTP 1.0 规范,Authorization 的格式是: Authorization: <type> <authorization-parameters> w3c规定,请求头Authorization用于验证用户身份。这就是告诉我们,token应该写在请求头Authorization中 …...

一篇理解TCP协议
一、TCP协议概念。 TCP(Transmission Control Protocol,传输控制协议)是一种面向连接的、可靠的传输层协议。它主要用于在计算机网络中,通过建立可靠的通信连接来进行数据传输。 TCP协议的特点如下: 可靠性…...

rk平台android12系统设置里面互联网选项中的以太网选项点击不了问题
rk平台android12系统中,系统设置中的互联网选项,当连接以太网以后,会显示以太网的选项,但是点击没作用,现在需要点击能够进入到以太网的设置界面,需要添加相关的点击事件。 首先,在packages/apps/Settings/AndroidManifest.xml中的以太网设置配置添加一个action,用于打…...

ctrl+d和ctrl+c的区别
CtrlD和CtrlC都是常用的键盘快捷键,但它们的功能不同。 CtrlD 在不同的操作系统和应用程序中可以有不同的功能。在Unix/Linux系统的命令行终端中,CtrlD的作用是发送EOF(End of File)信号,表示输入结束。在Windows系统中…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

Spark 之 入门讲解详细版(1)
1、简介 1.1 Spark简介 Spark是加州大学伯克利分校AMP实验室(Algorithms, Machines, and People Lab)开发通用内存并行计算框架。Spark在2013年6月进入Apache成为孵化项目,8个月后成为Apache顶级项目,速度之快足见过人之处&…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

【CSS position 属性】static、relative、fixed、absolute 、sticky详细介绍,多层嵌套定位示例
文章目录 ★ position 的五种类型及基本用法 ★ 一、position 属性概述 二、position 的五种类型详解(初学者版) 1. static(默认值) 2. relative(相对定位) 3. absolute(绝对定位) 4. fixed(固定定位) 5. sticky(粘性定位) 三、定位元素的层级关系(z-i…...

Nuxt.js 中的路由配置详解
Nuxt.js 通过其内置的路由系统简化了应用的路由配置,使得开发者可以轻松地管理页面导航和 URL 结构。路由配置主要涉及页面组件的组织、动态路由的设置以及路由元信息的配置。 自动路由生成 Nuxt.js 会根据 pages 目录下的文件结构自动生成路由配置。每个文件都会对…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...
