RSA攻击:Smooth攻击
目录
前言:缘起
P-1光滑攻击
P+1光滑攻击
前缀知识
Lucas-Subsquence(卢卡斯序列)
编码实现与理解
小试牛刀
[NCTF 2019]childRSA
引用
前言:缘起
Smooth攻击(光滑攻击),在最近刷题的时候总是能偶尔蹦跶到我的脑子里面。不是天天遇见它,而是其背后的原理总是让人头痛。所以,为了解决心头大患,只好尽自己所能搜罗网上资料理解Smooth攻击背后的数学原理。特此来记录这几天克服中的重重险阻时,迸发的灵感。
光滑攻击有两种:p-1光滑攻击,p+1光滑攻击。其中p-1光滑攻击是容易理解的,理解他并非什么难事。网上也不缺少它的证明,但是p+1光滑攻击则恰恰相反。首先,它违反人类感觉上的认知(编码上),所以阅读代码解析时困难,其次理论知识需要一定储备,所以学习上成本较大。因此,本文会对前者做出证明和记录,对后者给出部分性质证明以及一些个人的理解。
下面就进入正文啦~
P-1光滑攻击
P-1光滑攻击的底层原理,比较符合我们的小学认知。我们先给出一些定义以及结论。
定义1:一个数n可以被分解为若干小质数的乘积,则称其为光滑数。
定义2:若一个光滑数最大的小质数因子 <= B, 则称其为 B-光滑数。
即 n =
。
特此说明,定义2中的表达式解释中应当满足这条关系:。
从上面的两个定义中,我们不难可以得出一个事实。如果光滑数N的小质数因子互不相同,那么有 。也就是说,
。
正是因为B-光滑数的这一特性,加上给出的条件是p-1为光滑数,我们可以很自然的联想到使用费马小定理来配合求解。
以为下为p-1光滑数的证明:

通过上述证明,我们明确了因此P的可计算性,一旦N,P,Q知其二,那么RSA就得以破解。剩下的计算过程想必大家都了如指掌,就不展开说了。
上脚本
# 采用Python语言编写imoprt gmpy2def Pollards_p_1(N):a = 2 # 为了快速计算以及满足费马小定理条件n = 2 # 从1开始没必要while(True):a = pow(a, n, N) # 递推计算a^B!p = gmpy2.gcd(a - 1, N) # 尝试计算pif p != 1 and p != n: # 满足要求则返回return pn += 1P+1光滑攻击
在这种攻击方式下,底层的数学原理并非那么被人熟知或者被我们频繁使用。因此,我需要较大篇幅的导入一些前缀知识。如果你嫌弃篇幅过长的话,可以根据目录索引至代码部分的理解。
前缀知识
Lucas-Subsquence(卢卡斯序列)
这个名字有些令人陌生,确实它不如它的“好兄弟”,Fiboncci,那般有名气。现在,我们直接给出卢卡斯序列的样子(在密码学应用中),,于是,我们可以使用特征根将其求解。先将原式子变换为
,得到两个根为
。因此,等于
。带入n = 1时,由待定系数法可知,λ = 1。
接下来,我们需要找到卢卡斯序列的最小循环节。令s = 。


注意:两个多项式出去首位两项,其他的偶数都是p的配属二次项系数决定了p已知存在。
编码实现与理解
当然有了一些潦草的前缀知识之后,我们并不能马上解出答案。因为这需要我们对RSA原过程做出一些变换,以及扩展一些数学知识。
引理1:对于卢卡斯序列,
成立。
引理可以通过通项式子证明,其次因为m,n位置可以到对调,所以我们不让m>n吧,这样序列就不有负下标。

根据前缀知识,我们了解到,S(N)一定是数列的一个循环周期,但不一定是最小周期。但是这已经够了。
def lucas(c, d, N):x = c # a1y = (c**2 - 2) % N # a2for bit in bin(d)[3:]: # 快速乘(从高到低位)--我个人理解if bit == '1':x = (x*y - c) % N # 下标对应a_{x+y},其次保证a_{2k-1}=a_{k}a_{k-1}-a_{0}成立y = (y**2 - 2) % N # 使得y翻倍--正常的快速幂流程else:y = (x*y - c) % N # 保证a_{2k-1}=a_{k}a_{k-1}-a_{0}成立x = (x**2 - 2) % N # a_{k} 翻倍return x #返回a_{ed} 关于编码层面上采用快速乘的想法。源于引理1,由其可知,,
,且
。所以计算小标ed时,我们可以把d拆分为2进制数,依次用来完成快速乘。
小试牛刀
[NCTF 2019]childRSA
获取附件之后,我们可以看到以下代码段。

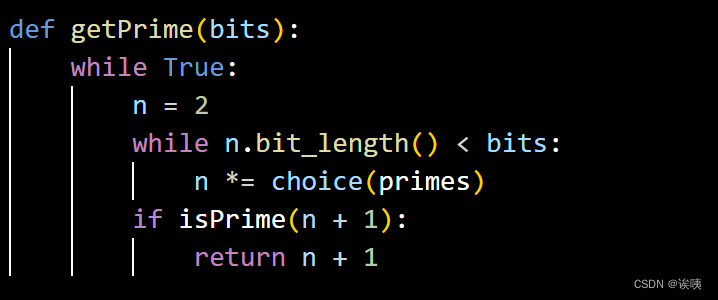
我们,容易分析出P、Q是自定义素数生成器生成的。因此,我们的重点核心来到解析素数生成器的原理。
通过 n *= choice(primes) 知道,这一通过小素数累积得到的,并且这些小素数互不相同。除此之外,我们发现最后的返回值为 n + 1,也就是说 p = n + 1,即 p - 1 是一个光滑数。因此,我们可以选择p-1光滑攻击。
def Pollards_p_1(N):a = 2 # 为了快速计算以及满足费马小定理条件n = 2 # 从1开始没必要while(True):a = pow(a, n, N)p = gmpy2.gcd(a - 1, N)if p != 1 and p != n:return pn += 1p = Pollards_p_1(n)由上诉代码段破解得到:
p = 178449493212694205742332078583256205058672290603652616240227340638730811945224947826121772642204629335108873832781921390308501763661154638696935732709724016546955977529088135995838497476350749621442719690722226913635772410880516639651363626821442456779009699333452616953193799328647446968707045304702547915799734431818800374360377292309248361548868909066895474518333089446581763425755389837072166970684877011663234978631869703859541876049132713490090720408351108387971577438951727337962368478059295446047962510687695047494480605473377173021467764495541590394732685140829152761532035790187269724703444386838656193674253139# 因此
q = n // p
phi = (p - 1) * (q - 1)
import primefac
e = 0x10001
d = primefac.modinv(e, phi)
c = 26308018356739853895382240109968894175166731283702927002165268998773708335216338997058314157717147131083296551313334042509806229853341488461087009955203854253313827608275460592785607739091992591431080342664081962030557042784864074533380701014585315663218783130162376176094773010478159362434331787279303302718098735574605469803801873109982473258207444342330633191849040553550708886593340770753064322410889048135425025715982196600650740987076486540674090923181664281515197679745907830107684777248532278645343716263686014941081417914622724906314960249945105011301731247324601620886782967217339340393853616450077105125391982689986178342417223392217085276465471102737594719932347242482670320801063191869471318313514407997326350065187904154229557706351355052446027159972546737213451422978211055778164578782156428466626894026103053360431281644645515155471301826844754338802352846095293421718249819728205538534652212984831283642472071669494851823123552827380737798609829706225744376667082534026874483482483127491533474306552210039386256062116345785870668331513725792053302188276682550672663353937781055621860101624242216671635824311412793495965628876036344731733142759495348248970313655381407241457118743532311394697763283681852908564387282605279108
m = pow(c, d, n)
print(long_to_bytes(m))从而我们获取flag:NCTF{Th3r3_ar3_1ns3cure_RSA_m0duli_7hat_at_f1rst_gl4nce_appe4r_t0_be_s3cur3}
引用
1.Cryptosystem on lucas - hash_hash
2.Wiki
相关文章:

RSA攻击:Smooth攻击
目录 前言:缘起 P-1光滑攻击 P1光滑攻击 前缀知识 Lucas-Subsquence(卢卡斯序列) 编码实现与理解 小试牛刀 [NCTF 2019]childRSA 引用 前言:缘起 Smooth攻击(光滑攻击),在最近刷题的时候总是能偶尔蹦跶到我的脑子里面。不是天天遇见它&am…...

什么是位域和位段?如何定义和使用位域?
位域(Bit Fields)是C语言中一种用于在数据结构中以位为单位对数据进行精确控制的技术。它们允许程序员将一个整数字段分割成多个更小的部分,每个部分可以存储不同的信息。位域通常在对内存节省要求高、数据压缩或硬件寄存器描述等情况下使用。…...

网络攻防备课笔记
从“踩点”到“创建后门”的攻击流程 踩点:攻击者在实施攻击前对目标进行初步的探索和调查的过程,包括收集目标的IP地址、开放的端口、服务版本、可能的漏洞等信息。 扫描:使用工具如Nmap、Masscan等对目标进行端口扫描,找出开放…...
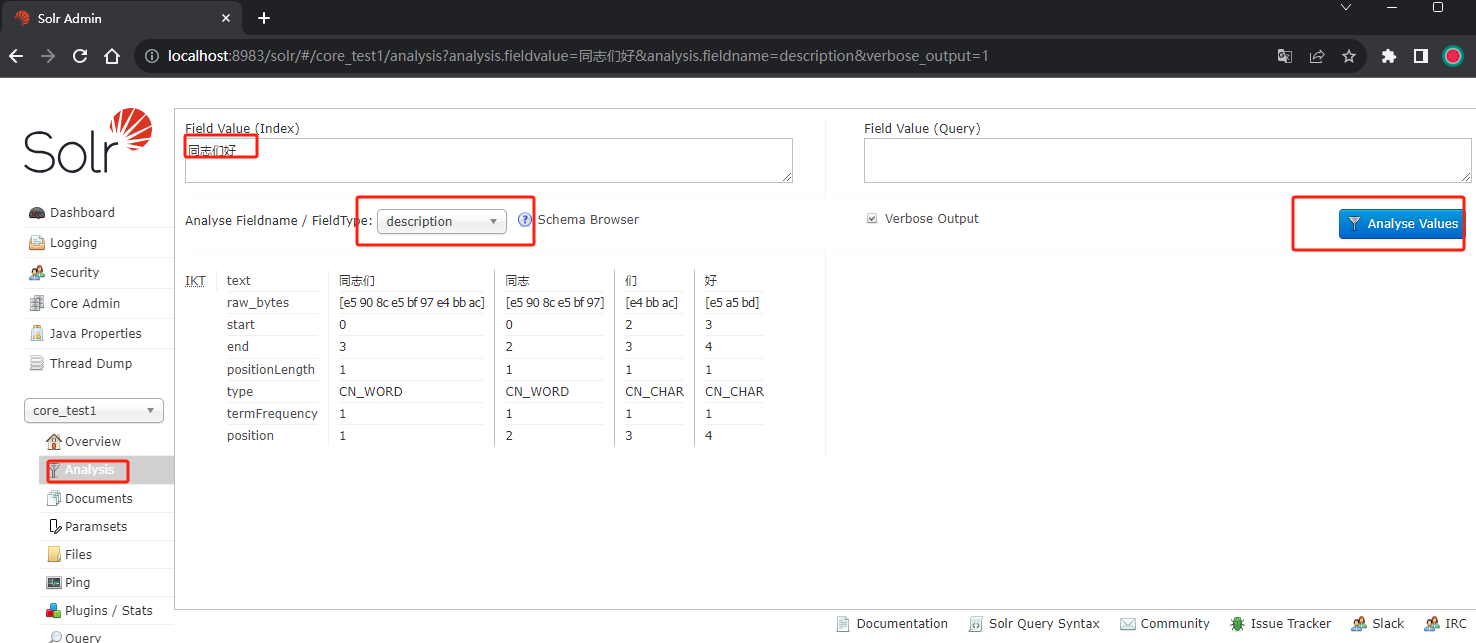
Apache Solr9.3 快速上手
Apache Solr 简介 Solr是Apache的顶级开源项目,使用java开发 ,基于Lucene的全文检索服务器。 Solr比Lucene提供了更多的查询语句,而且它可扩展、可配置,同时它对Lucene的性能进行了优化。 安装 下载 : 下载地址解压 : tar -zxv…...

按关键字搜索淘宝商品API接口获取商品销量、优惠价、商品标题等参数示例
关键词搜索商品接口的作用是提供搜索功能,让用户根据关键词在电商平台上搜索商品,并根据搜索条件和偏好获取相关的商品列表和推荐结果,提高用户购物体验和准确度。对于电商平台而言,这个接口也能帮助用户发现更多商品、提升销量和…...

【外汇天眼】价格波动的节奏感:优化止盈方法!
止盈,依然是一种经验,而不是一种技术。它涉及到价格波动的灵活应对,以确保我们不会错失潜在的盈利,同时也不会让盈利被逆市波动所侵蚀。以下是关于如何有效实施止盈策略的一些建议: 首先,我们要明确&#…...
VMvare虚拟机安装国产麒麟V10桌面操作系统
一、系统下载 进入银河麒麟官网:https://www.kylinos.cn/ 选择桌面操作系统,然后进入操作系统版本选择页面,选择银河麒麟桌面操作系统V10 选择后,进入系统介绍页面,然后点击申请试用 点击后进入申请页面…...
Golang--channel+waitGroup控制并发量
文章目录 channelwaitGroup控制并发量前言示例 channelwaitGroup控制并发量 前言 golang的goroutine非常轻量级,同时启动数万协程都没问题。如果不对并发量进行控制,比如同时产生数百万的协程,会压垮服务器通过控制channel缓冲区的大小&…...

前端【响应式图片处理】之 【picture标签】
目录 🌟前言🌟目前最常见的解决方案🌟新的解决方案<picture>🌟<picture>的工作原理🌟<picture> 兼容性解决方案🌟写在最后 🌟前言 哈喽小伙伴们,前端开发过程中经…...

js实现链式调用,查询和处理数据
实现一个 query 方法,实现对数据的链式查询和处理 要求如下 query 传入参数为原始数据(数组格式,每个元素都是对象) 通过进行链式调用对数据执行操作,支持的方法有where(predicate): 根据参数的条件进行筛选࿰…...
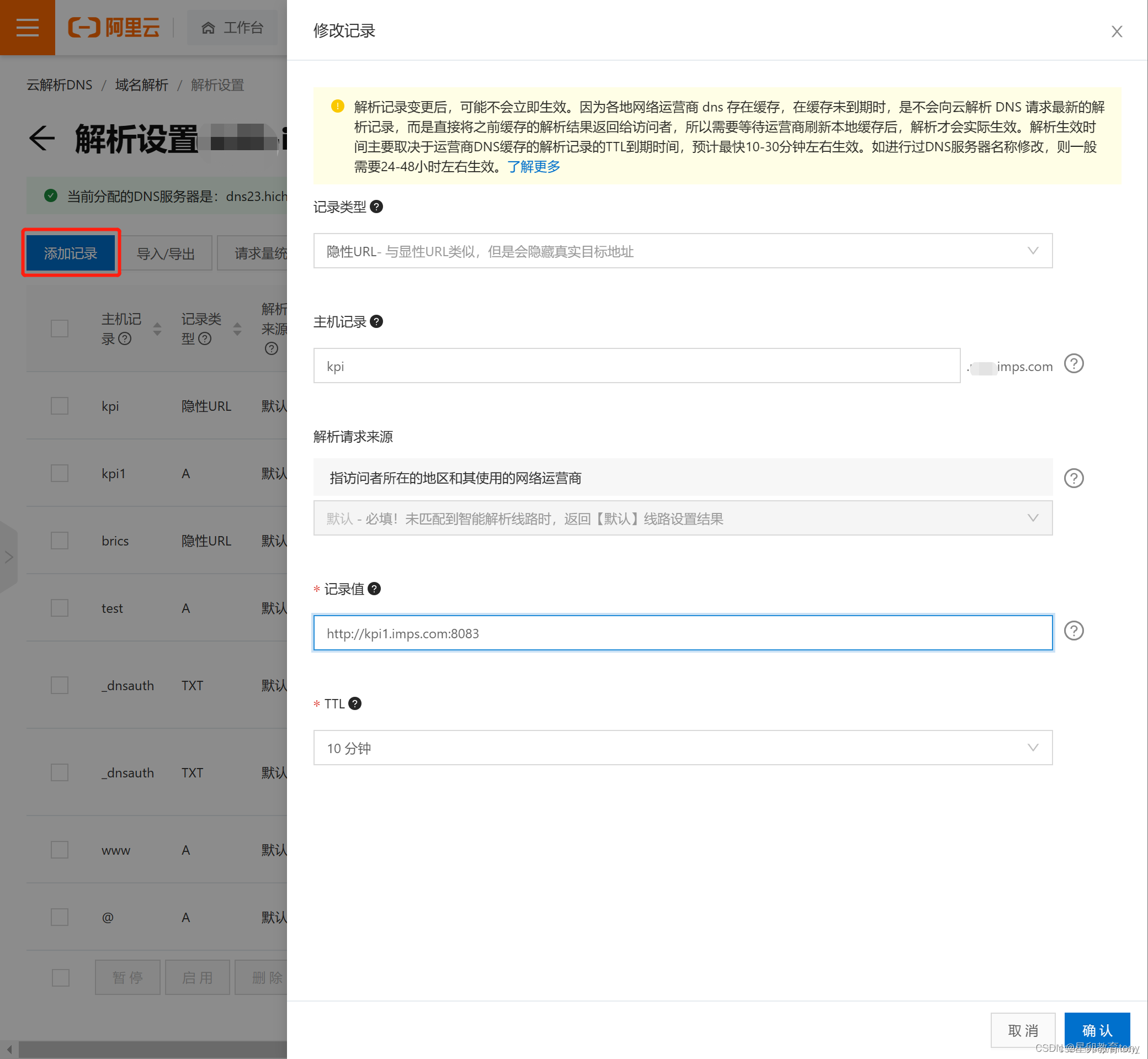
阿里云 腾讯云 配置二级域名并解析指向非80端口操作指南
目标:主域名 imps.com 已完成配置,新增配置 kpi.imps.com 等二级域名并指向 8083 端口。 (此操作需要主域名已经通过备案3天后,最好指向的IP地址网站也通过了备案申请,否则会提示域名没有备案。) 操作流程…...

菜单子节点的写法
菜单子节点的写法 1.测试数据2.实现代码3.获取父ID层级 1.测试数据 1.表结构SQL CREATE TABLE test (id int DEFAULT NULL,u_id int DEFAULT NULL,p_u_id int DEFAULT NULL ) ENGINEInnoDB DEFAULT CHARSETutf8mb4 COLLATEutf8mb4_general_ci;2.数据SQL INSERT INTO test (i…...

系统架构设计:9 论软件系统架构评估及其应用
目录 一 架构评估的意义 1 性能 2 可用性 3 安全性 4 可修改性 5 易用性...
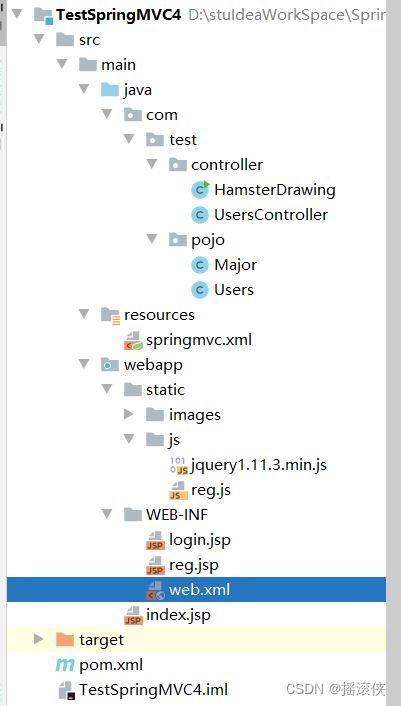
javaee SpringMVC中json的使用
jsp <%--Created by IntelliJ IDEA.User: 呆萌老师:QQ:2398779723Date: 2019/12/6Time: 15:55To change this template use File | Settings | File Templates. --%> <% page contentType"text/html;charsetUTF-8" language"java" %> <%St…...

【系统架构】软件架构的演化和维护
导读:本文整理关于软件架构的演化和维护知识体系。完整和扎实的系统架构知识体系是作为架构设计的理论支撑,基于大量项目实践经验基础上,不断加深理论体系的理解,从而能够创造新解决系统相关问题。 目录 1、软件架构演化和定义 …...

一盏茶的功夫帮你彻底搞懂JavaScript异步编程从回调地狱到async/await
🎬 江城开朗的豌豆:个人主页 🔥 个人专栏 :《 VUE 》 《 javaScript 》 ⛺️ 生活的理想,就是为了理想的生活 ! 目录 📘 1. 引言 📘 2. 使用方法 📘 3. 实现原理 📘 4. 写到最后…...
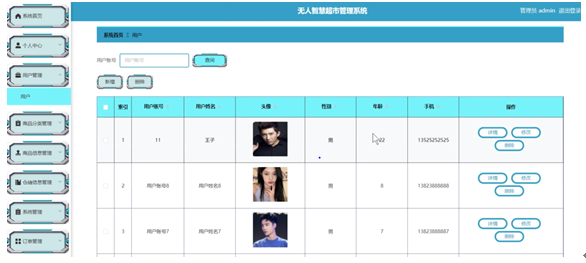
前后端分离计算机毕设项目之基于SpringBoot的无人智慧超市管理系统的设计与实现《内含源码+文档+部署教程》
博主介绍:✌全网粉丝10W,前互联网大厂软件研发、集结硕博英豪成立工作室。专注于计算机相关专业毕业设计项目实战6年之久,选择我们就是选择放心、选择安心毕业✌ 🍅由于篇幅限制,想要获取完整文章或者源码,或者代做&am…...
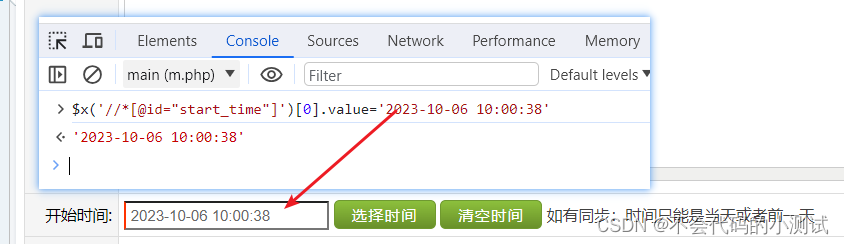
从0开始python学习-31.selenium 文本输入框、下拉选择框、文件上传、时间插件选择元素定位
目录 1. 纯文本输入框 2. 存在默认值的文本输入 3. 下拉选择框 4. 输入后下拉选择框 5. 文件上传 6. 时间插件 1. 纯文本输入框 driver.find_element(By.XPATH,/html/body/div[2]/td[2]/input).send_keys(测试名称) 2. 存在默认值的文本输入 注意: 1. 这种存…...

MyCat-web安装文档:安装Zookeeper、安装Mycat-web
安装Zookeeper A. 上传安装包 zookeeper-3.4.6.tar.gzB. 解压 #解压到当前目录,之后会生成一个安装后的目录 tar -zxvf zookeeper-3.4.6.tar.gz#加上-c 代表解压到指定目录 tar -zxvf zookeeper-3.4.6.tar.gz -C /usr/local/C. 在安装目录下,创建数据…...
Ajax跨域访问,访问成功但一直走error不走success的的问题解决
Ajax跨域访问,访问成功但一直走error不走success的的问题解决 通过搜索各种资料,终于解决啦,废话不多说了,还是老规矩直接上代码: 我这里用了jsonp,有想了解的点击 : jsonp 前端代码: $.ajax({type:post…...
: K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?)
云原生核心技术 (7/12): K8s 核心概念白话解读(上):Pod 和 Deployment 究竟是什么?
大家好,欢迎来到《云原生核心技术》系列的第七篇! 在上一篇,我们成功地使用 Minikube 或 kind 在自己的电脑上搭建起了一个迷你但功能完备的 Kubernetes 集群。现在,我们就像一个拥有了一块崭新数字土地的农场主,是时…...

阿里云ACP云计算备考笔记 (5)——弹性伸缩
目录 第一章 概述 第二章 弹性伸缩简介 1、弹性伸缩 2、垂直伸缩 3、优势 4、应用场景 ① 无规律的业务量波动 ② 有规律的业务量波动 ③ 无明显业务量波动 ④ 混合型业务 ⑤ 消息通知 ⑥ 生命周期挂钩 ⑦ 自定义方式 ⑧ 滚的升级 5、使用限制 第三章 主要定义 …...

UDP(Echoserver)
网络命令 Ping 命令 检测网络是否连通 使用方法: ping -c 次数 网址ping -c 3 www.baidu.comnetstat 命令 netstat 是一个用来查看网络状态的重要工具. 语法:netstat [选项] 功能:查看网络状态 常用选项: n 拒绝显示别名&#…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...
