C++算法:寻找两个正序数组的中位数
题目
寻找两个正序数组的中位数
给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。
算法的时间复杂度应该为 O(log (m+n)) 。
示例 1:
输入:nums1 = [1,3], nums2 = [2]
输出:2.00000
解释:合并数组 = [1,2,3] ,中位数 2
示例 2:
输入:nums1 = [1,2], nums2 = [3,4]
输出:2.50000
解释:合并数组 = [1,2,3,4] ,中位数 (2 + 3) / 2 = 2.5
2023年3月13号的解法
class Solution {
public:
double findMedianSortedArrays(vector& nums1, vector& nums2) {
const int Len = nums1.size() + nums2.size();
const int iAvg1 = Rec(nums1.data(), nums1.data() + nums1.size(), nums2.data(), nums2.data() + nums2.size(), (Len - 1) / 2);
if (Len & 1)
{
return iAvg1;
}
const int iAvg2 = Rec(nums1.data(), nums1.data() + nums1.size(), nums2.data(), nums2.data() + nums2.size(), (Len - 1) / 2+1);
return (iAvg1 + iAvg2) / 2.0;
}
int Rec(int* b1, int* e1, int* b2, int* e2, int iFindIndex)
{
if (b1 == e1)
{
return b2[iFindIndex];
}
if (b2 == e2)
{
return b1[iFindIndex];
}
if (0 == iFindIndex)
{
return min(*b1, *b2);
}
int k = (iFindIndex + 1) / 2;
const int index1 = min(k - 1,(int)( e1 - b1)-1);
const int index2 = min(k - 1, (int)(e2 - b2 )- 1);
if (b1[index1] < b2[index2])
{
return Rec(b1 + index1 + 1, e1, b2, e2, iFindIndex - index1 - 1);
}
return Rec(b1, e1, b2 + index2 + 1, e2, iFindIndex - index2 - 1);
}
};
2023年8月6号的解法
class Solution {
public:
double findMedianSortedArrays(vector& nums1, vector& nums2) {
m_c = nums1.size() + nums2.size();
m_iHalf = m_c / 2;
int left = 0, r = min(m_iHalf, (int)nums1.size()) + 1;//左闭右开
while (r > left + 1)
{
const auto mid = left + (r - left) / 2;
const int leftLen2 = m_iHalf - mid;
const int iRet = Cmp(mid, leftLen2, nums1, nums2);
if (0 == iRet)
{
break;
}
else if (iRet < 0)
{
r = mid;
}
else
{
left = mid;
}
}
if (m_dRet < 0 )
{
Cmp(left,m_iHalf-left,nums1,nums2);
}
return m_dRet;
}
int Cmp(int leftLen1, int leftLen2, const vector& nums1, const vector& nums2)
{
if (leftLen2 > nums2.size())
{
return 1;
}
int iLeftMax = INT_MIN;
if (leftLen1 > 0)
{
iLeftMax = max(iLeftMax, nums1[leftLen1 - 1]);
}
if (leftLen2 > 0)
{
iLeftMax = max(iLeftMax, nums2[leftLen2 - 1]);
}
int iRightMin = INT_MAX;
if (leftLen1 < nums1.size())
{
iRightMin = min(iRightMin, nums1[leftLen1]);
}
if (leftLen2 < nums2.size())
{
iRightMin = min(iRightMin, nums2[leftLen2]);
}
if (iLeftMax <= iRightMin)
{
if (1 & m_c)
{
m_dRet = iRightMin;
}
else
{
m_dRet = (iLeftMax + iRightMin) / 2.0;
}
return 0;
}
if ((leftLen1 > 0) && (nums1[leftLen1 - 1] > iRightMin))
{
return-1;
}
return 1;
}
double m_dRet=-1;
int m_c;
int m_iHalf;
};
其它
视频课程
如果你觉得复杂,想从简单的算法开始,可以学习我的视频课程。
https://edu.csdn.net/course/detail/38771
我的其它课程
https://edu.csdn.net/lecturer/6176
测试环境
win7 VS2019 C++17
相关下载
doc版文档,排版好
https://download.csdn.net/download/he_zhidan/88348653
相关文章:

C++算法:寻找两个正序数组的中位数
题目 寻找两个正序数组的中位数 给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。 算法的时间复杂度应该为 O(log (mn)) 。 示例 1: 输入:nums1 [1,3], nums2 [2] 输…...

2.1 关系数据结构及形式化定义
思维导图: 2.1.1 关系 笔记: 关系数据库模型是一个简单但强大的方式来表示数据及其之间的关系。下面是这节的关键内容: - **关系模型核心概念** * 关系数据模型的核心是“关系”,它在逻辑上表现为一个二维表。 * 此表中&a…...
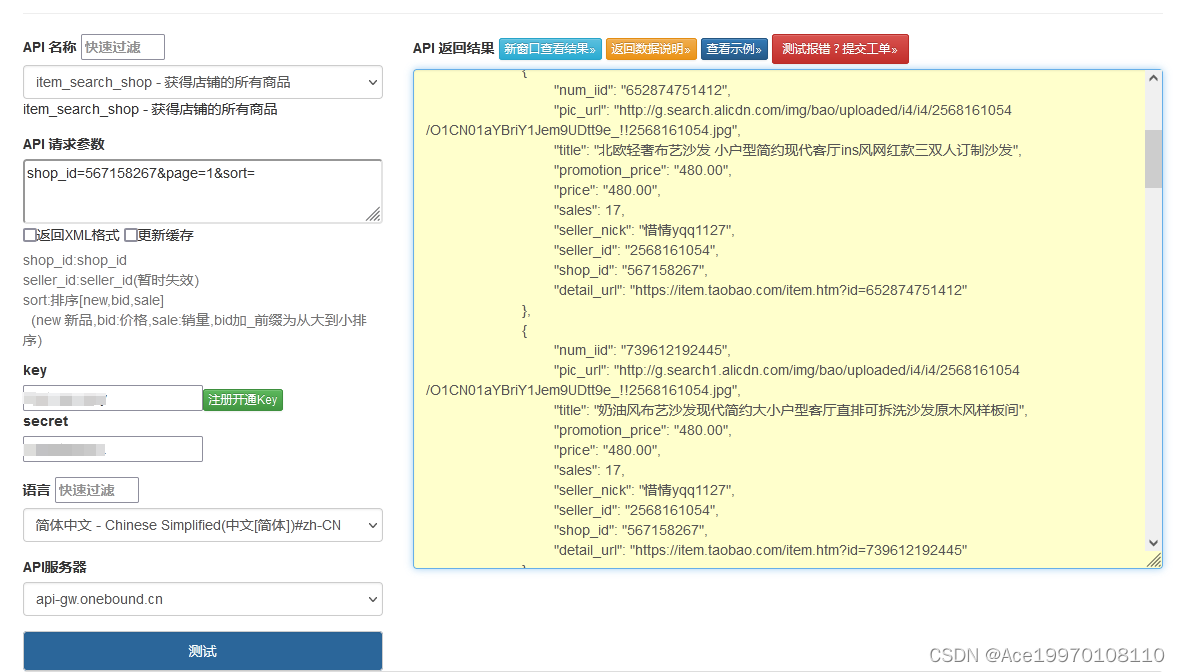
“揭秘淘宝店铺所有商品接口:一键获取海量热销宝贝信息!“
淘宝店铺所有商品接口可以通过shop id或店铺主链接获取到整店商品,数据包括:商品ID,图片地址,店铺标题,优惠价,价格,销量,宝贝链接等整个店铺的商品。 要使用这个接口,需…...

跟着播客学英语-Why I use vim ? part two
在上一期作者讲到了他使用 Vim 的主要原因是提高效率,不需要再去使用鼠标,今天我们继续上次未听完的内容: if you type Vi, thats going to be alias to Vim anyway by default theres, not really a good reason for you to use vi that I c…...
【网络通信三要素】TCP与UDP快速入门
网络通信三要素 1.什么是网络编程? 可以让设备中的程序,与网络上其他设备中的程序进行数据交互,从而实现网络通信的手段,java.net.*包下提供了网络编程的解决方案 2.基本的通信架构 基本的通信架构有2种形式:CS架构…...

k8s集群的简单搭建
K8S简单集群搭建 前提条件 windos11电脑,内存16g以上安装vmware虚拟机软件安装三个centos7虚拟机,分配硬盘40g,内存4g,CPU4核心网络均采用NAT模式(新建虚拟机默认的模式) centos7镜像下载:https://mirrors.tuna.tsi…...

语义分割笔记(三):通过opencv对mask图片来画分割对象的外接椭圆
文章目录 mask图像介绍步骤代码 mask图像介绍 根据 mask 图像来画分割对象的外接椭圆是一种常见的图像分割任务。Mask 图像通常是一个二值图像,其中包含了感兴趣对象的像素。通常情况下,白色像素表示对象,黑色像素表示背景。 步骤 以下是一…...

Nosql redis高可用和持久化
Nosql redis高可用和持久化 1、redis高可用2、redis持久化2.1redis持久化2.2Redis 持久化方法2.3RDB 持久化2.3.1RDB持久化工作原理2.3.2触发条件2.3.3其他自动触发机制2.3.4执行流程2.3.5启动时加载 2.4AOF 持久化2.4.1AOF持久化原理2.4.2开启AOF2.4.3执行流程2.4.4文件重写的…...
)
软件工程(1、2;5~7小测参考答案)
目录 软件工程第1、2章小测 需求工程第5-7章小测 软件工程第1、2章小测 一 单项选择题(12分) 1、下列关于软件开发的描述不正确的是()。(1分) 软件是独立于计算机硬件的一部分,但它又依赖于计算机硬件。 软件既是一种复杂的逻辑实体,又是一种工具。 软件的核心是程序,…...

服务器存储面临的两大难题
服务器存储面临的两大难题 服务器存储为核心的IT系统承受着业务发展带来的巨大压力: 随着业务发展,IT应用数量不断增多,当前数据中心的IT基础设施愈加复杂,服务器、存储等设备的数量不断增加。服务器与存储管理更加复杂:随着业务应用对IT基础…...

Blind Signature盲签名与fabric区块链结合的应用
盲签名的概念 首先由 David Chaum 于1982年提出,盲签名实现了签名者对发送者的消息进行签名,却不能知道签名者消息的具体内容。 相当于将文件放入信封,签名者在信封上对文件进行签名,而不知道具体的文件内容。 盲签名的实现方式…...
ueditor
下载文件 文档 UEditor入门部署 入门部署和体验 1.1 下载编辑器 到官网下载 UEditor 最新版:http://ueditor.baidu.com/website/download.html#ueditor 1.2 创建demo文件 解压下载的包,在解压后的目录创建 demo.html 文件,填入下面的…...
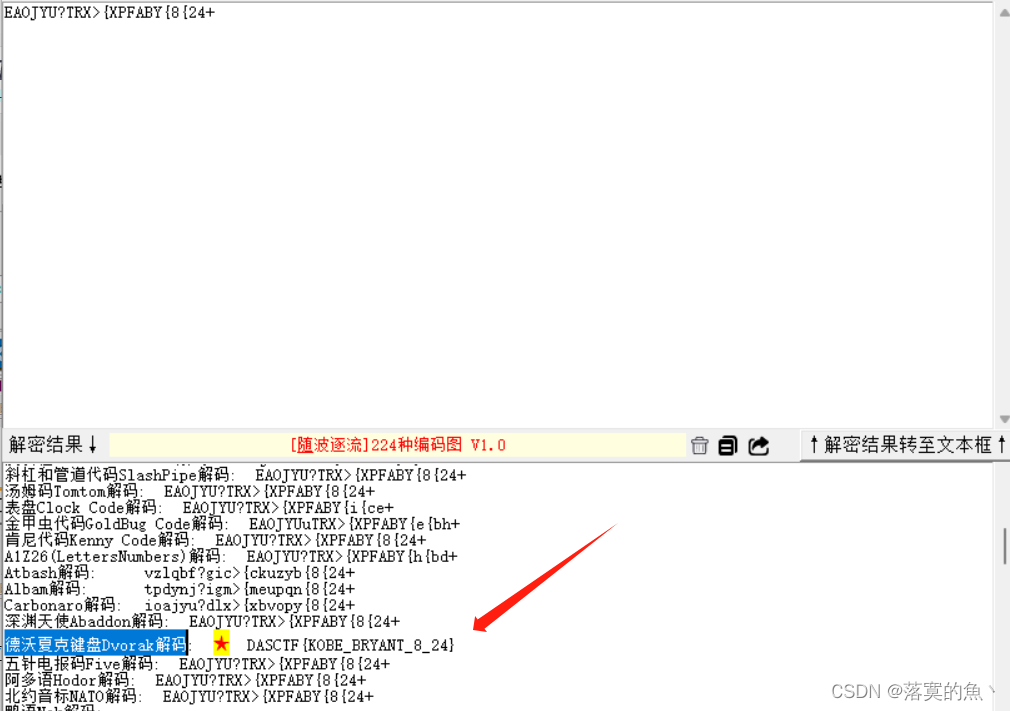
2023年台州市第三届网络安全技能大赛(MISC)—Black Mamba
前言:当时比赛没有做出来现在来复现一下 就当记录一下(这个思路没想到) Black Mamba: 一张图片 常规得分离,属性,LSB,盲水印等都尝试过 无果! 考点:异或解密࿰…...
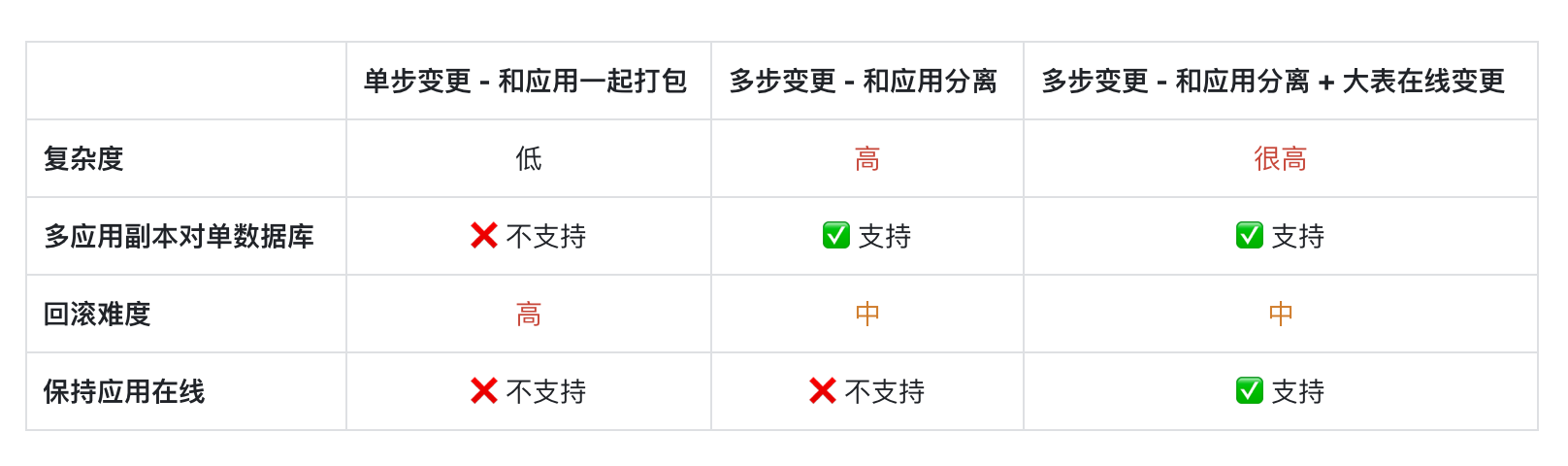
这道面试题工作中经常碰到,但 99% 的程序员都答不上来
小时候都被问过一个脑筋急转弯,把大象放进冰箱有几个步骤?我们一开始都会抓耳挠腮,去想着该如何把大象塞进冰箱。最终揭晓的答案却根本不关心具体的操作方法,只是提供了 3 个步骤组成的流程,「把冰箱打开,把…...

Linux安装单机PostgreSQL15.4
1. 联网rpm安装 1.1.关闭服务 ## 关闭防火墙 systemctl stop firewalld.service systemctl disable firewalld.service ## 关闭 selinux cat /etc/selinux/config SELINUXdisabled1.2.安装yum源 yum install -y https://download.postgresql.org/pub/repos/yum/reporpms/EL-…...

最新 SpringCloud微服务技术栈实战教程 微服务保护 分布式事务 课后练习等
SpringCloud微服务技术栈实战教程,涵盖springcloud微服务架构Nacos配置中心分布式服务等 SpringCloud及SpringCloudAlibaba是目前最流行的微服务技术栈。但大家学习起来的感受就是组件很多,不知道该如何应用。这套《微服务实战课》从一个单体项目入手&am…...
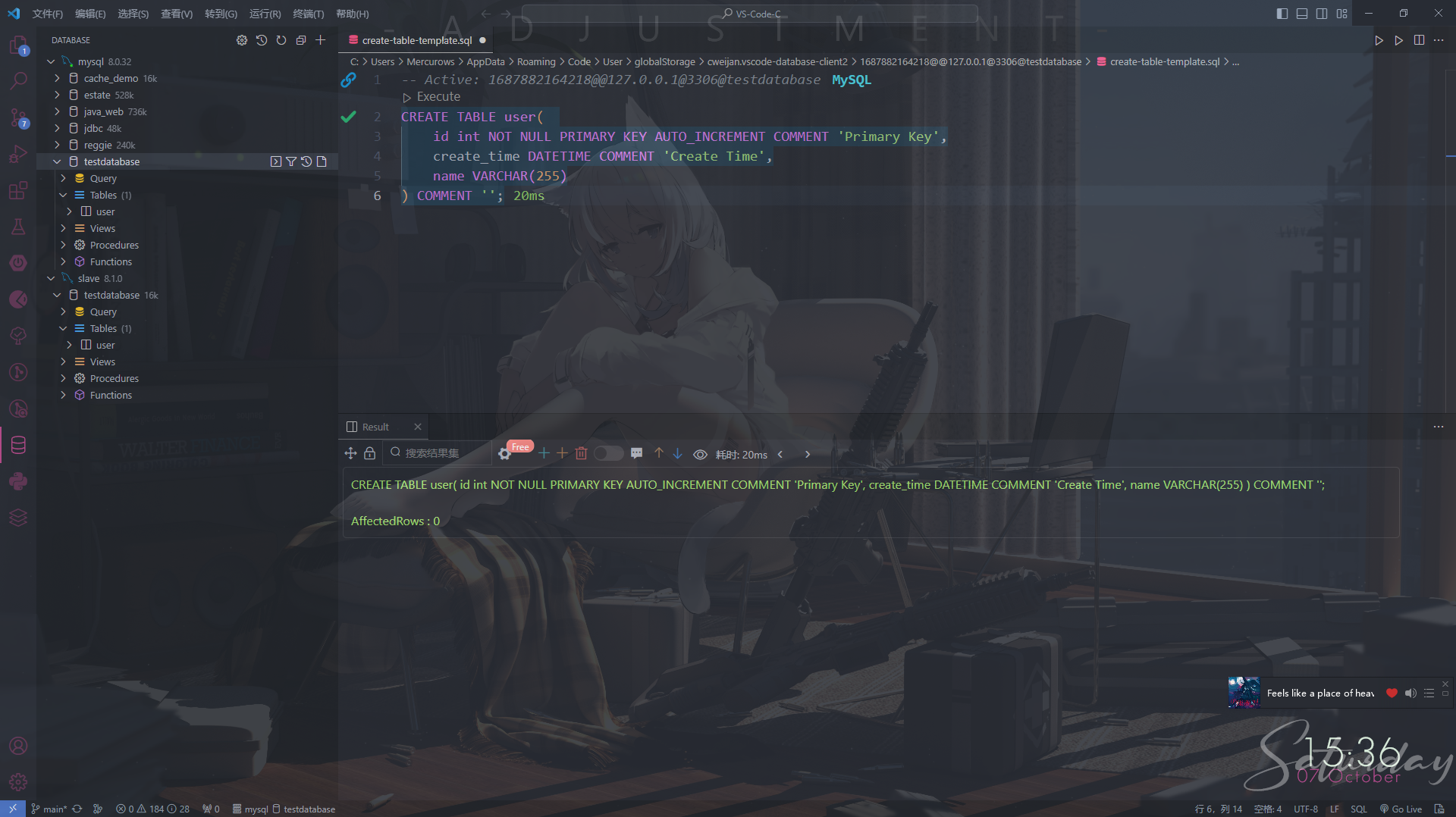
Docker搭建MySQL8.0主从复制(一主一从)
0. 配置说明 宿主机使用的版本为19045的win10专业版,MySQL使用的是8.0,Docker容器使用Linux。 1. 安装Docker Desktop 略 修改Docker默认安装路径 安装包自己就提供了修改安装路径的功能,CMD中运行: “Docker Desktop Installe…...
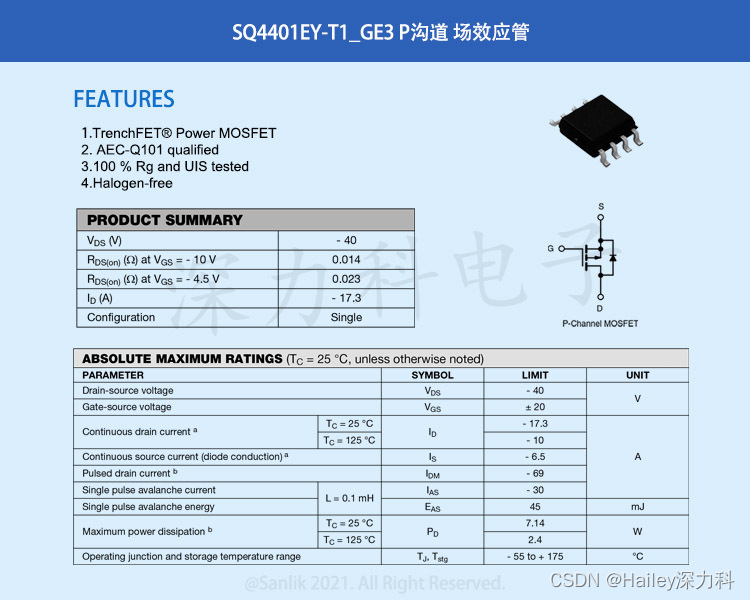
40V汽车级P沟道MOSFET SQ4401EY-T1_GE3 工作原理、特性参数、封装形式—节省PCB空间,更可靠
AEC-Q101车规认证是一种基于失效机制的分立半导体应用测试认证规范。它是为了确保在汽车领域使用的分立半导体器件能够在严苛的环境条件下正常运行和长期可靠性而制定的。AEC-Q101认证包括一系列的失效机制和应力测试,以验证器件在高温、湿度、振动等恶劣条件下的可…...
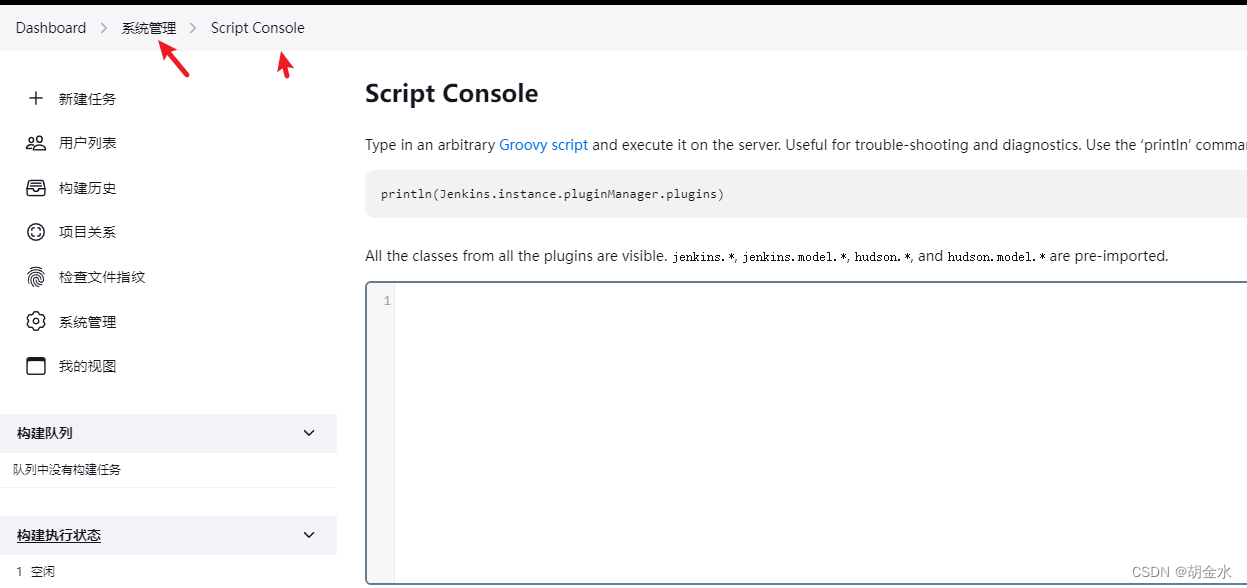
记录在搭建Jenkins时,所遇到的坑,以及解决方案
项目场景: 记录在搭建Jenkins时,所遇到的坑,以及解决方案.问题描述1 在使用Jenkins构建时,报错如下: cp: cannot stat /project/xx/xxxx/dist/: No such file or directory Build step Execute shell marked build as failure Finished: FAILURE解决方…...
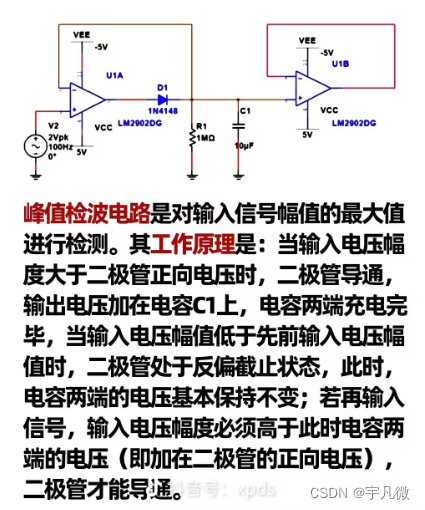
二极管“天马行空”的作用,你知道吗?
网友:二极管怎么有这么多种类呀? 工程师:二极管可以说除了电阻电容外用的比较多的一种元器件,起到的作用多着呢 那么二极管都可以起到哪些作用呢: 一、防反作用,主回路中串联一个二极管,是利用…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

多模态商品数据接口:融合图像、语音与文字的下一代商品详情体验
一、多模态商品数据接口的技术架构 (一)多模态数据融合引擎 跨模态语义对齐 通过Transformer架构实现图像、语音、文字的语义关联。例如,当用户上传一张“蓝色连衣裙”的图片时,接口可自动提取图像中的颜色(RGB值&…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

MySQL中【正则表达式】用法
MySQL 中正则表达式通过 REGEXP 或 RLIKE 操作符实现(两者等价),用于在 WHERE 子句中进行复杂的字符串模式匹配。以下是核心用法和示例: 一、基础语法 SELECT column_name FROM table_name WHERE column_name REGEXP pattern; …...

HDFS分布式存储 zookeeper
hadoop介绍 狭义上hadoop是指apache的一款开源软件 用java语言实现开源框架,允许使用简单的变成模型跨计算机对大型集群进行分布式处理(1.海量的数据存储 2.海量数据的计算)Hadoop核心组件 hdfs(分布式文件存储系统)&a…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...

论文阅读笔记——Muffin: Testing Deep Learning Libraries via Neural Architecture Fuzzing
Muffin 论文 现有方法 CRADLE 和 LEMON,依赖模型推理阶段输出进行差分测试,但在训练阶段是不可行的,因为训练阶段直到最后才有固定输出,中间过程是不断变化的。API 库覆盖低,因为各个 API 都是在各种具体场景下使用。…...
