鱼眼相机去畸变(图像拉直/展开/矫正)算法及实战总结
本文介绍两种方法
1、经纬度矫正法
2、棋盘格矫正法
一、经纬度矫正法

1、算法说明
经纬度矫正法, 可以把鱼眼图想象成半个地球, 然后将地球展开成地图,经纬度矫正法主要是利用几何原理, 对图像进行展开矫正。
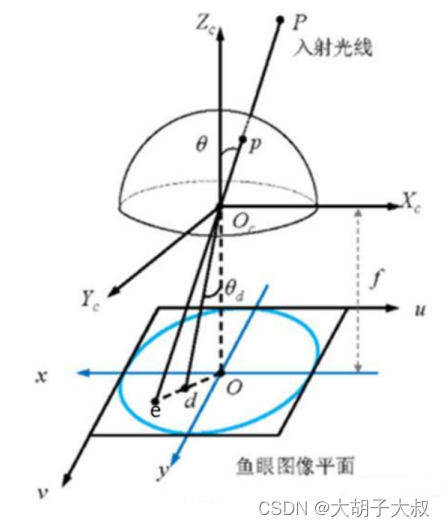
经过P点的入射光线没有透镜的话,本应交于相机成像平面的e点。然而,经过鱼眼相机的折射,光线会交于相机成像平面的d点,就产生了畸变,因此畸变图像整体上呈现出像素朝图像中心点聚集的态势。
而去畸变,就是将折射到d点的点,重新映射回到e点,因此去畸变之后的图像与原始的鱼眼图像相比,仿佛是把向心聚集的像素又重新向四周铺展开来。
详细的推导流程及公式见地址:AVM环视系统——鱼眼相机去畸变算法 - 知乎
2、 代码
import math
from PIL import Imageim = Image.open("/Users/Fisheye_photo-600x600.jpg")
im.show()width, high = im.size
sqrt_len = min(width, high)
im = im.transform((sqrt_len, sqrt_len),Image.EXTENT,((width-sqrt_len)/2, (high-sqrt_len)/2, sqrt_len+(width-sqrt_len)/2, sqrt_len+(high-sqrt_len)/2))
width = high = sqrt_lenidata = im.getdata()
odata = []alpha = math.pi/2out_high = round(high * math.tan(alpha/2))
out_width = round(width * math.tan(alpha/2))
out_radius = round(high * math.tan(alpha/2))
out_center_x = out_width / 2
out_center_y = out_high / 2out_bl_x = 0
out_br_x = out_width - 1
out_bt_y = 0
out_bb_y = out_high - 1out_bl_cx = out_bl_x - out_center_x
out_br_cx = out_br_x - out_center_x
out_bt_cy = out_bt_y - out_center_y
out_bb_cy = out_bb_y - out_center_ysrc_radius = round(high * math.sin(alpha/2))
src_center_x = width / 2
src_center_y = high / 2for i in range(0, high * width):ox = math.floor(i / out_width)oy = i % out_highcx = ox - out_center_x;cy = oy - out_center_y;out_distance = round(math.sqrt(pow(cx, 2) + pow(cy, 2)))theta = math.atan2(cy, cx)if (-math.pi/4 <= theta <= math.pi/4):bx = out_radius * math.cos(math.pi/4)by = bx * math.tan(theta)elif (math.pi/4 <= theta <= math.pi*3/4):by = out_radius * math.sin(math.pi/4)bx = by / math.tan(theta)elif (-math.pi*3/4 <= theta <= -math.pi/4):by = out_radius * math.sin(-math.pi/4)bx = by / math.tan(theta)else:bx = out_radius * math.cos(-math.pi*3/4)by = bx * math.tan(theta)bdy_distance = round(math.sqrt(pow(cx, 2) + pow(cy, 2)))src_distance = src_radius * bdy_distance / out_radiussrc_x = round(src_center_x + math.cos(theta) * src_distance)src_y = round(src_center_y + math.sin(theta) * src_distance)src_idx = src_x*width + src_y if(0 < src_idx < high*width):odata.append(idata[src_idx])else:odata.append((0,0,0))om = Image.new("RGB", (high, width))
om.putdata(odata)
om.show()3、代码及图片地址:GitHub - duducosmos/defisheye: Fast Corrects for fisheye distortion in an image.
二、棋盘格矫正方法
1、算法说明
利用棋盘格进行标定, 然后计算鱼眼镜头的畸变系数以及内参, opencv中自带有fisheye模块, 可以直接根据棋盘格标定结果,采用cv2.fisheye.calibrate计算畸变系数以及内参, 然后使用cv2.fisheye.initUndistortRectifyMap函数计算映射矩阵, 最后根据映射矩阵, 使用cv2.remap进行矫正。
2、代码
import cv2
import numpy as np
import math
import time# 鱼眼有效区域截取
def cut(img):img_gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)(_, thresh) = cv2.threshold(img_gray, 20, 255, cv2.THRESH_BINARY)contours, hierarchy = cv2.findContours(thresh, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE)cnts = sorted(contours, key=cv2.contourArea, reverse=True)[0]x,y,w,h = cv2.boundingRect(cnts)r = max(w/ 2, h/ 2)# 提取有效区域img_valid = img[y:y+h, x:x+w]return img_valid, int(r)# 鱼眼矫正
def undistort(src,r):# r: 半径, R: 直径R = 2*r# Pi: 圆周率Pi = np.pi# 存储映射结果dst = np.zeros((R, R, 3))src_h, src_w, _ = src.shape# 圆心x0, y0 = src_w//2, src_h//2for dst_y in range(0, R):theta = Pi - (Pi/R)*dst_ytemp_theta = math.tan(theta)**2for dst_x in range(0, R):# 取坐标点 p[i][j]# 计算 sita 和 fiphi = Pi - (Pi/R)*dst_xtemp_phi = math.tan(phi)**2tempu = r/(temp_phi+ 1 + temp_phi/temp_theta)**0.5tempv = r/(temp_theta + 1 + temp_theta/temp_phi)**0.5if (phi < Pi/2):u = x0 + tempuelse:u = x0 - tempuif (theta < Pi/2):v = y0 + tempvelse:v = y0 - tempvif (u>=0 and v>=0 and u+0.5<src_w and v+0.5<src_h):dst[dst_y, dst_x, :] = src[int(v+0.5)][int(u+0.5)]# 计算在源图上四个近邻点的位置# src_x, src_y = u, v# src_x_0 = int(src_x)# src_y_0 = int(src_y)# src_x_1 = min(src_x_0 + 1, src_w - 1)# src_y_1 = min(src_y_0 + 1, src_h - 1)## value0 = (src_x_1 - src_x) * src[src_y_0, src_x_0, :] + (src_x - src_x_0) * src[src_y_0, src_x_1, :]# value1 = (src_x_1 - src_x) * src[src_y_1, src_x_0, :] + (src_x - src_x_0) * src[src_y_1, src_x_1, :]# dst[dst_y, dst_x, :] = ((src_y_1 - src_y) * value0 + (src_y - src_y_0) * value1 + 0.5).astype('uint8')return dstif __name__ == "__main__":t = time.perf_counter()frame = cv2.imread('../imgs/pig.jpg')cut_img,R = cut(frame)result_img = undistort(cut_img,R)cv2.imwrite('../imgs/pig_nearest.jpg',result_img)print(time.perf_counter()-t)效果图
 3、代码地址
3、代码地址
https://github.com/HLearning/fisheye
三、总结:比对两个算法
本人用两个算法对一张图像进行拉直,发现经过经纬度矫正算法生成的图像原作者裁剪掉了边缘部分,见下图效果图,中间黑框内的图像是经过“经纬度矫正法”得到的效果图,外面的大图是用“棋盘格矫正法”得到的效果图

为了更直观,更改了图像的透明度,可以看出两个算法的效果还是多少有些差别的。
其实,两个算法的边缘部分都被严重拉伸,丢不丢掉看适用场景和个人需要吧。
四、知识拓展
立体标定

算法说明
坐标映射建立,各区域的角点都有一维世界坐标为0,对应图5中三幅子图像分别为Y=0,X=0,Z=0。根据棋盘方格边长以及与世界坐标原点间隔的方格数,可得到所有角点的世界坐标。从而建立起二维图像坐标与三维世界坐标的一一映射,用于模型参数的求解。
参考地址:采用立体标定板的鱼眼相机快速标定方法_真空技术_新闻动态_深圳市鼎达信装备有限公司
基于双经度模型的鱼眼图像畸变矫正方法
基于双经度模型的鱼眼图像畸变矫正方法 - 百度文库
相关文章:

鱼眼相机去畸变(图像拉直/展开/矫正)算法及实战总结
本文介绍两种方法 1、经纬度矫正法 2、棋盘格矫正法 一、经纬度矫正法 1、算法说明 经纬度矫正法, 可以把鱼眼图想象成半个地球, 然后将地球展开成地图,经纬度矫正法主要是利用几何原理, 对图像进行展开矫正。 经过P点的入射光线…...

es6 数据类型
es6 数据类型 map 数据类型 >Map 对象保存键值对。 用途 : Object的key无法支持该数据时需要了解对象大小时 map 数据类型任何值(对象或者原始值) 都可以作为一个键。 Object 的键只能是字符串 let myMap new Map(); let myMap1 new Map(); var keyStrin…...

【postgresql】
看到group by 1,2 和 order by 1, 2。看不懂,google,搜到了Stack Overflow 上有回答 What does SQL clause “GROUP BY 1” mean? 大概意思就是,group by, order by 后面跟数字,指的是 selec…...

【C++】空间配置器 allocator:原理及底层解析
文章目录 空间配置器一级空间配置器二级空间配置器1. 内存池2. SGI-STL中二级空间配置器设计 - - 哈希桶3. 二级空间配置器的空间申请 空间配置器的默认选择空间配置器的在封装:添加了数据类型大小空间配置器对象的构造与析构 容器中的 allocator 空间配置器 提到空…...
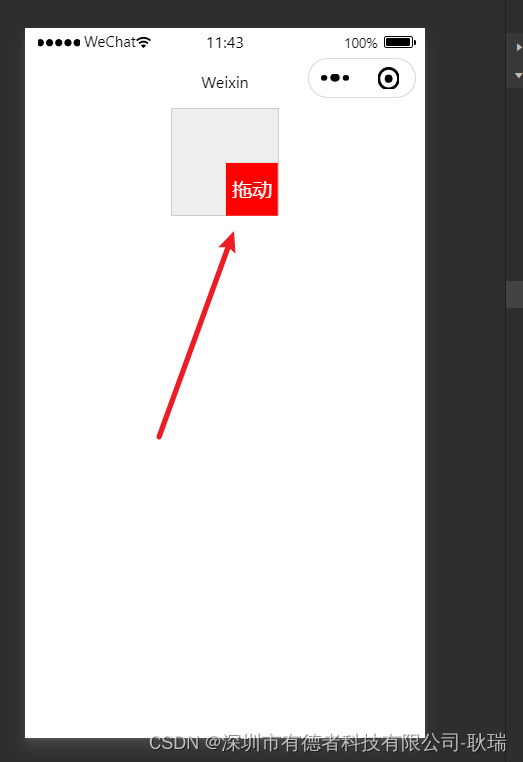
微信小程序 movable-area 区域拖动动态组件演示
movable-area 组件在小程序中的作用是用于创建一个可移动的区域,可以在该区域内拖动视图或内容。这个组件常用于实现可拖动的容器或可滑动的列表等交互效果。 使用 movable-area 组件可以对其内部的 movable-view 组件进行拖动操作,可以通过设置不同的属…...

隔离上网,安全上网
SDC沙盒数据防泄密系统(安全上网,隔离上网) •深信达SDC沙盒数据防泄密系统,是专门针对敏感数据进行防泄密保护的系统,根据隔离上网和安全上网的原则实现数据的代码级保护,不会影响工作效率,不…...

NOSQL Redis 数据持久化 RDB、AOF(二) 恢复
redis 执行flushall 或 flushdb 也会产生dump.rdb文件,但里面是空的。 注意:千万执行,不然rdb文件会被覆盖的。 dump.rdb 文件如何恢复数据 讲备份文件 dump.rdb 移动到redis安装目录并启动服务即可。 dump.rdb 自动触发 和手动触发 自…...
UDP通信
UDP通信 #include <sys/types.h> #include <sys/socket.h> ssize_t sendto(int sockfd, const void *buf, size_t len, int flags,const struct sockaddr *dest_addr, socklen_t addrlen); - 参数:- sockfd : 通信的fd- buf : 要发送的数据- len : 发送…...

Bootstrap对溢出内容的两种处理:滚动条和隐藏两种方式
Bootstrap中定义了以下两个类来处理内容溢出的情况: 类overflow-auto:在固定宽度和高度的元素上,如果内容溢出了元素,将生成一个垂直滚动条,通过滚动条可以查看溢出的内容。 类overflow-hidden:在固定宽度和高度的元素…...
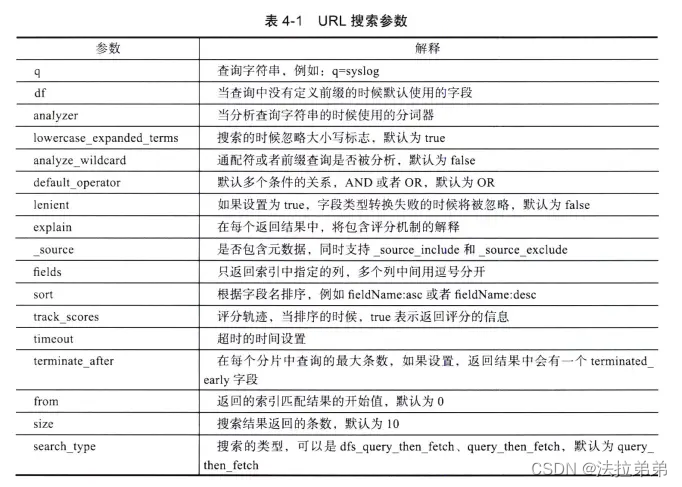
elasticsearch基本语法
这里写自定义目录标题 elasticsearch简介基本语法索引创建索引修改索引删除索引 查询简单查询精确查询条件查询范围查询:聚合查询:排序和分页: 参考文献: elasticsearch简介 Elasticsearch 是一个开源的分布式搜索和分析引擎&…...

Maven Spring jar包启动报错 排查
Maven Spring jar包启动报错排查 背景 maven 编译jar包,放在linux服务器启动不起来,提示:xxxx-0.0.1-SNAPSHOT.jar中没有主清单属性 原因 pom 配置文件,多了 <skip>true</skip> <build><plugins>&l…...

LeetCode-2485-找出中枢整数
题目描述: 给你一个正整数 n ,找出满足下述条件的 中枢整数 x : 1 和 x 之间的所有元素之和等于 x 和 n 之间所有元素之和。 返回中枢整数 x 。如果不存在中枢整数,则返回 -1 。题目保证对于给定的输入,至多存在一个中…...
)
nano pi m1配置脚本(全志H3)
为nanopi m1写一个自动配置脚本,简化自己的操作 配置:H3芯片,1G内存,64G卡 系统:friendlycore focal 4.14版本 一、系统安装 烧录系统后,插入机器,但是使用df -ih发现只有900K的nodesÿ…...
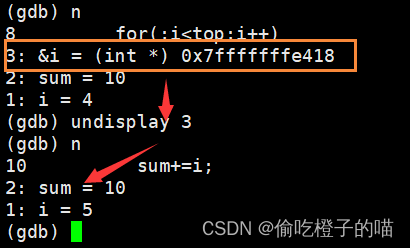
linux--gdb的使用
1,Makefile默认release版本,要想进入debug版本需添加-g后缀 2,进入调试界面:gdb 可执行程序 3,显示代码:l(list) 数字(1/0) 不停回车可一直显示到结束并显…...
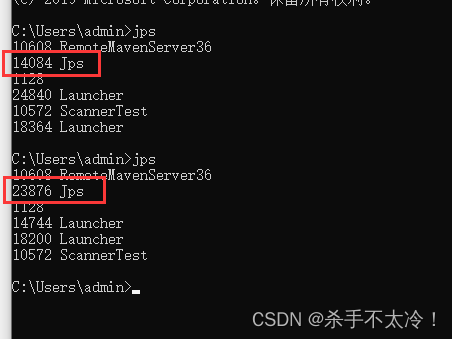
JVM命令行监控工具
JVM命令行监控工具 概述 性能诊断是软件工程师在日常工作中需要经常面对和解决的问题,在用户体验至上的今天,解决好应用的性能问题能带来非常大的收益。 Java作为最流行的编程语言之一,其应用性能诊断一直受到业界广泛关注,可能…...

系统架构设计:4 论微服务架构及其应用
目录 一 微服务架构 1 微服务 2 微服务架构的优点 3微服务面临的挑战...
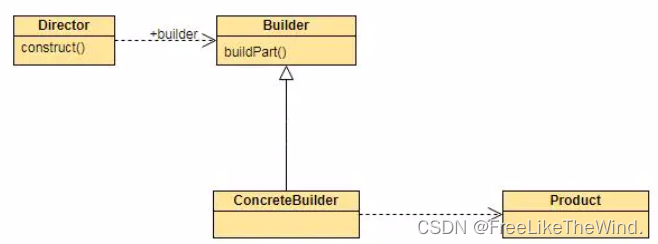
【C++设计模式之建造者模式:创建型】分析及示例
简介 建造者模式(Builder Pattern)是一种创建型设计模式,它将复杂对象的构建过程与其表示分离,使得同样的构建过程可以创建不同的表示。 描述 建造者模式通过将一个复杂对象的构建过程拆分成多个简单的部分,并由不同…...
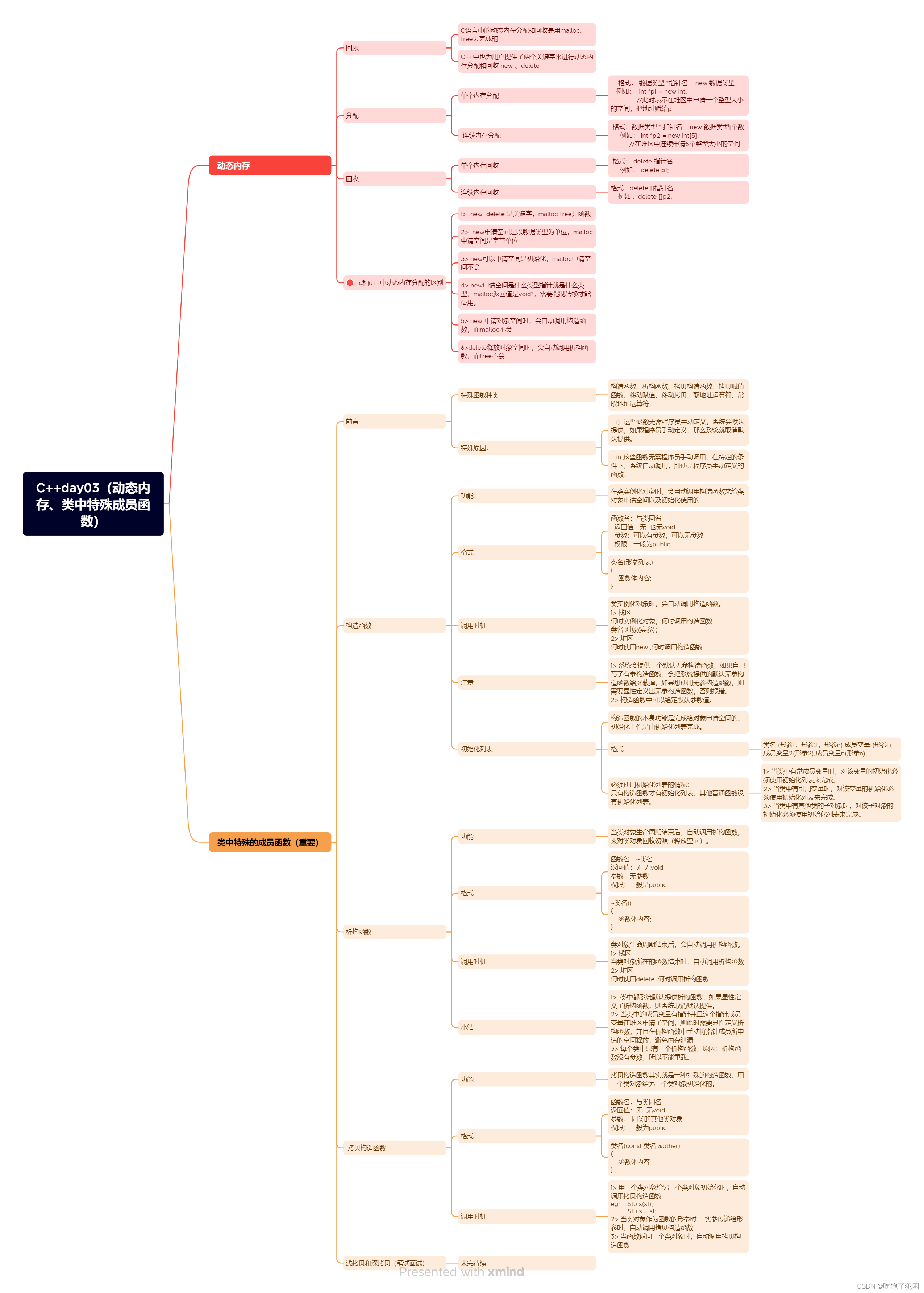
C++day03(动态内存、类中特殊成员函数)
今日任务 1> 思维导图 2> 设计一个Per类,类中包含私有成员:姓名、年龄、指针成员身高、体重,再设计一个Stu类,类中包含私有成员:成绩、Per类对象p1,设计这两个类的构造函数、析构函数和拷贝构造函数。 代码: …...

【Leetcode】179. 最大数
一、题目 1、题目描述 给定一组非负整数 nums,重新排列每个数的顺序(每个数不可拆分)使之组成一个最大的整数。 注意:输出结果可能非常大,所以你需要返回一个字符串而不是整数。 示例1: 输入:nums = [10,2] 输出:"210"示例2: 输入:nums = [3,30,34,5…...

ArduPilot开源飞控之AP_Baro_MSP
ArduPilot开源飞控之AP_Baro_MSP 1. 源由2. back-end抽象类3. 方法实现3.1 AP_Baro_MSP3.2 update3.3 handle_msp3.4 MSP UART port 4. 参考资料 1. 源由 鉴于ArduPilot开源飞控之AP_Baro中涉及Sensor Driver有以下总线类型: I2CSerial UARTCANSITL //模拟传感器(…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...
